Himawari-8卫星云下海表温度反演的机器学习方法比较研究

范冬林,杨鑫,曾优,何宏昌,付波霖

(1.桂林理工大学 测绘地理信息学院,广西 桂林 541006;2.桂林理工大学 生态时空大数据感知服务重点实验室,广西 桂林 541006)

0 引言

高精度海表温度(sea surface temperature,SST)是研究海洋的重要参数之一,被广泛用于研究海洋气候和水域生态系统,是预估海洋和大气之间复杂关系的基础物理变量[1]。海洋动力(漩涡、上升流、锋面等)变化特征和海洋灾害(黑潮、台风等)均与海表温度变化密切相关[2-3]。海表温度不仅是评估全球变暖的重要物理变量,同时是局部生态系统健康指标。因此,构建高精度、高空间覆盖率的海表温度是一项非常重要的任务。

卫星遥感技术由于具有监测尺度大、覆盖范围广的特点,被广泛用于对海表温度的获取。基于卫星的红外辐射计使用黑体辐射定理可以方便地估算海表温度[4]。此类方法以辐射出射度与热力学温度关系为基础,使用多波段差消除不同气体对辐射的影响[5],进而建立多波段亮温和SST的拟合方程。如美国国家航空航天局海洋生物处理小组基于中分辨率成像光谱仪(moderate-resolution imaging spectroradiometer,MODIS)红外波段开发的非线性海表温度算法[6]、Mcclain等[7]根据多个通道开发的多通道海表温度算法。这一类算法及其派生算法作为业务化方法被广泛用于反演卫星SST产品,包括美国国家海洋与大气应用管理局、美国国家航空航天局和欧洲气象卫星开发组织等提供的SST产品。然而,这类算法受限于云干扰,易受不同气体及气溶胶对辐射的影响[8],无法准确评估在云遮挡情况下的海表温度,在云广泛存在的热带地区云遮挡问题尤为突出。

由于云层覆盖,传统SST反演算法导致云层下垫面海表温度的缺失。为了提高海表温度覆盖率,需针对缺失的海表温度数据进行预估。利用多种卫星海表温度产品进行数据融合或者利用时序的海表温度产品数据进行海温预估[9-10]是提高海表温度覆盖率的常用方法。然而,上述方法不能实现遥感卫星海温数据的实时补缺。如静止卫星Himawari-8卫星影像数据,由于成像频率远高于极轨卫星,难以利用其他卫星温度产品进行融合。因此,通过遥感红外热辐射直接反演海表温度是提高静止卫星海表温度产品覆盖率的主要方法。目前卫星红外图像云下海表温度反演的研究有限,少部分研究开展了单一条件下(卷云)海表温度反演[11-12]、云类型分组条件下海表温度反演[13],但尚未有文献针对Himawari-8卫星数据开展云下海表温度反演。因此,为了弥补这项研究的缺失,本文基于近红外波段(λ=1 609.8 nm)瑞利校正后的阈值建立6种不同阈值区间的样本数据集,利用机器学习算法探究在不同阈值区间下云下海表温度的反演性能。本文建立的算法可以有效提高Himawari-8卫星单次成像下海表温度的空间覆盖率。

1 数据源与数据处理

1.1 数据源及数据匹配

Himawari-8是日本气象厅发射的一颗覆盖西太平洋和东亚地区的静止气象卫星,以10 min超短周期作业,其红外波段空间分辨率为2 km×2 km,是葵花系列卫星的一种。其搭载的高级葵花成像仪(advanced himawari imager,AHI)传感器共有16个通道,为3个可见光、3个近红外以及10个红外通道[14]。

本文使用已进行辐射校正和几何校正的L1级数据作为遥感数据源。实测海表温度数据为2019年、2020年日本气象厅海洋浮标采集的海表温度,该数据的采样频率为1 h,本文选取采集区域位于15°N～45°N,120°E～170°E的海洋浮标海表温度实测数据。为保证实测数据的正确性,本文对浮标实测海表温度数据进行质量监测。首先,通过数据预处理删除重复的数据,监测数据空间位置的合理性,删除空间位置在陆地和近海岸区域的数据。其次,监测数据内部一致性,对同一个浮标采集的数据进行噪声过滤,其过滤过程如下[15]:由于实测SST在某些采样频率存在数据缺失问题,因此,先对缺失数据进行插值。本文设置插值滑动窗口为5 h,即当前点SSTi在[SSTi-5,SSTi+5]范围内存在实测值时才满足插值条件,插值方法直接使用滑动窗口内的均值;对插值后的实测数据进行连续性判断,如果断裂则分割为一个片段,当片段中的SST数据值小于10个,直接忽略该片段;对每一个片段利用孤立森林[16]进行异常检测,剔除异常值;最后只在实测SST数据中选取非异常值的数值作为合理的SST。图1展示了其中一个浮标设备实测数据进行去噪后的结果,图2为剔除噪声后实测数据的空间分布以及有云和无云的数据直方图,其中有云和无云数据通过Himawari-8卫星云产品数据判别。

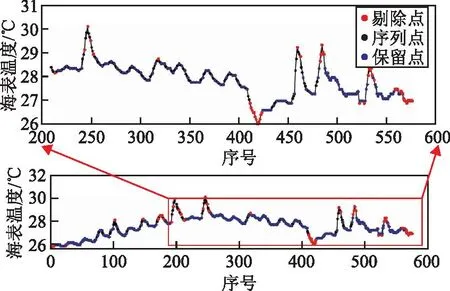
图1 海表温度实测数据噪声去除结果

图2 实测数据空间分布和直方图

然后对去噪后的实测数据与Himawari-8卫星L1级数据进行匹配。数据匹配方法是以实测数据时空信息为基准,先匹配实测点时间在±10 min以内的Himawari-8卫星L1级全盘数据,然后以实测点空间位置为中心,选择3×3窗口计算单元,并计算第5波段(λ=1 609.8 nm)反照率(albedo)在该窗口内的平均值和标准差,如果中心像元的值超过2倍的标准差,则忽略该匹配点。由于Himawari-8卫星L1 1～6波段存储的并非大气顶层反射率,需要按照式(1)对其转换为ρTOA。

(1)

式中:ρ是大气层顶(top of atmosphere,TOA)的表现反射率;θ是太阳天顶角。

1.2 数据预处理

数据匹配后的数据集需进行云识别以便于开发和训练有云、无云情况下的模型。云的种类多、厚度参差不一且随时序动态变化,导致卫星采集存在云干扰的数据易产生多样性及复杂性。如果存在云,则辐射传输时将改变传输的方向,在数据中表现出反射率增大、亮度温度降低。出现误差主要是部分辐射来源于云顶,这成为云下海表温度预估时的重大阻碍。基于阈值方法被最早运用云的判别,是一种高效且准确的方法[17]。例如,在开阔海域,利用近红外波段(SeaWiFSλ=865 nm,MODISλ=869 nm)瑞利校正后的阈值0.027判别是否有云[18];在近岸海域,利用短波红外(MODISλ=1 240 nm)瑞利校正后的阈值0.023 5进行近岸海域云检测[19]。本文采用阈值方法,根据瑞利散射原理,利用6S模型计算第5波段(λ=1 609.8 nm)的瑞利校正反射率值进行云层判别,并将其标记为云层值(RC5),后文中将以该值为依据划分有云情况下的样本。与标准6S模型不同是,本文将Himawari-8卫星第5波段的光谱响应函数作为波长参数进行瑞利校正。根据实验,阈值为0.125时无云数据和Himawari-8卫星官方提供的云掩膜数据最匹配,二者的相似度达到92%。因此,RC5≤0.125被认为是无云,RC5>0.125被认为是有云。然后,不断增大RC5的阈值,构建不同阈值下的样本集。由于6S模型无法判别剔除太阳天顶角(solar zenith angle,SOZ)大于70°时是否存在云,在对匹配点对进行瑞利校正时,剔除SOZ大于70°的数据。

2 方法

为了评估不同机器学习方法在有云和无云情况下海表温度反演的精度,本文基于3种典型的机器学习算法以评估RC5阈值递增变化情况下海表温度反演性能。3种算法都是拟合数据关系并依据原理具有针对性的选取,MLP对特征值的加权侧重无云情况下拟合数据关系;RFR随机选取训练数据侧重对偶然误差的消除;SVR空间降低维度侧重有云情况下处理复杂的训练数据。

MLP由输入层、输出层和一个或多个隐含层构成,隐含层类似回归性函数逼近器并且包含多个神经元,单个神经元是输入层特征值赋予权重后添加非线性激活函数,其本身是神经网络模型[20]。为了模型更准确地进行预估,需要使用优化器不断迭代选取最佳权重,本文使用每层具有100个隐藏单元的5个隐藏层,激活函数为ReLU,优化器为adam,迭代次数5 000次的模型参数进行模型训练。RFR使用回归器对决策树的结果按照权重进行合并。使用bootstrap算法引入随机性,将样本数据有放回地进行取样,组建子样本并用于构建决策树,在每个树种的分裂点选取部分特征来判定特征与目标值之间的关系,通过树深度决定每棵树对样本数据的学习程度。本文使用决策树数量为1 000,最大特征值为5,以训练RFR模型。支持向量机是自监督的非参数统计学习技术,它使用径向基核函数将特征变量从低维映射到高维空间,在分类中使用超平面将特征变量划分为不同类型,以此为基础衍生出SVR。在本文中,通过迭代不同核函数(线性、多项式、高斯、径向基等)以确定各阈值样本集合的最优模型。

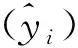
3 实验结果与分析

3.1 输入特征构建

海表温度反演模型的特征包括从Himawari-8卫星获得的10个波段亮温值以及传感器成像的4个几何参数,即太阳天顶角、太阳方位角(solar azimuth angle,SOA)、卫星天顶角(satellite zenith angle,SAZ)和卫星方位角(satellite azimuth angle,SAA)。考虑到近红外和红外波段在辐射传输模型中其离水反射率约为0,这些波段瑞利校正后的遥感反射率仅受气溶胶和云的影响。因此,本文将Himawari-8卫星第4波段(近红外)、第5波段、第6波段(红外)瑞利校正后的反射率作为特征引入模型。由于3.1～4.1 μm和10～12 μm是红外波段大气窗口存在的中心波长,本文根据物理算法将红外大气窗口波段相减作为亮温波段间的差值,一共扩展4个差值的特征。在实验过程中,由于SAZ和SAA过于集中,使得模型易造成模型发生过拟合现象,所以SAZ和SAA不作为模型输入特征。本文最终选取SOA、SOZ、RC4、RC5、RC6、BT7、BT8、BT9、BT10、BT11、BT12、BT13、BT14、BT15、D7-14、D13-15、D13-11、D13-14作为模型训练的输入特征变量,其中RC表示瑞利校正后的遥感反射率,BT表示亮温,D表示差值,数字代表Himawari-8卫星高级成像仪对应的波段序号。如RC5表示第5波段瑞利校正后的值,BT12表示第12波段的亮温,D13-15表示第13波段和第15波段亮温差。

3.2 模型性能评估

本文根据Himawari-8卫星第5波段瑞利校正后反射率,将样本数据按照阈值0.125、0.2、0.3、0.4、0.5和0.6共划分为6个等级的样本集合,各等级样本直方图如图3所示。图3中,N表示样本数量,RC5表示第5波段瑞利校正值,A表示阈值递增新增样本数量。

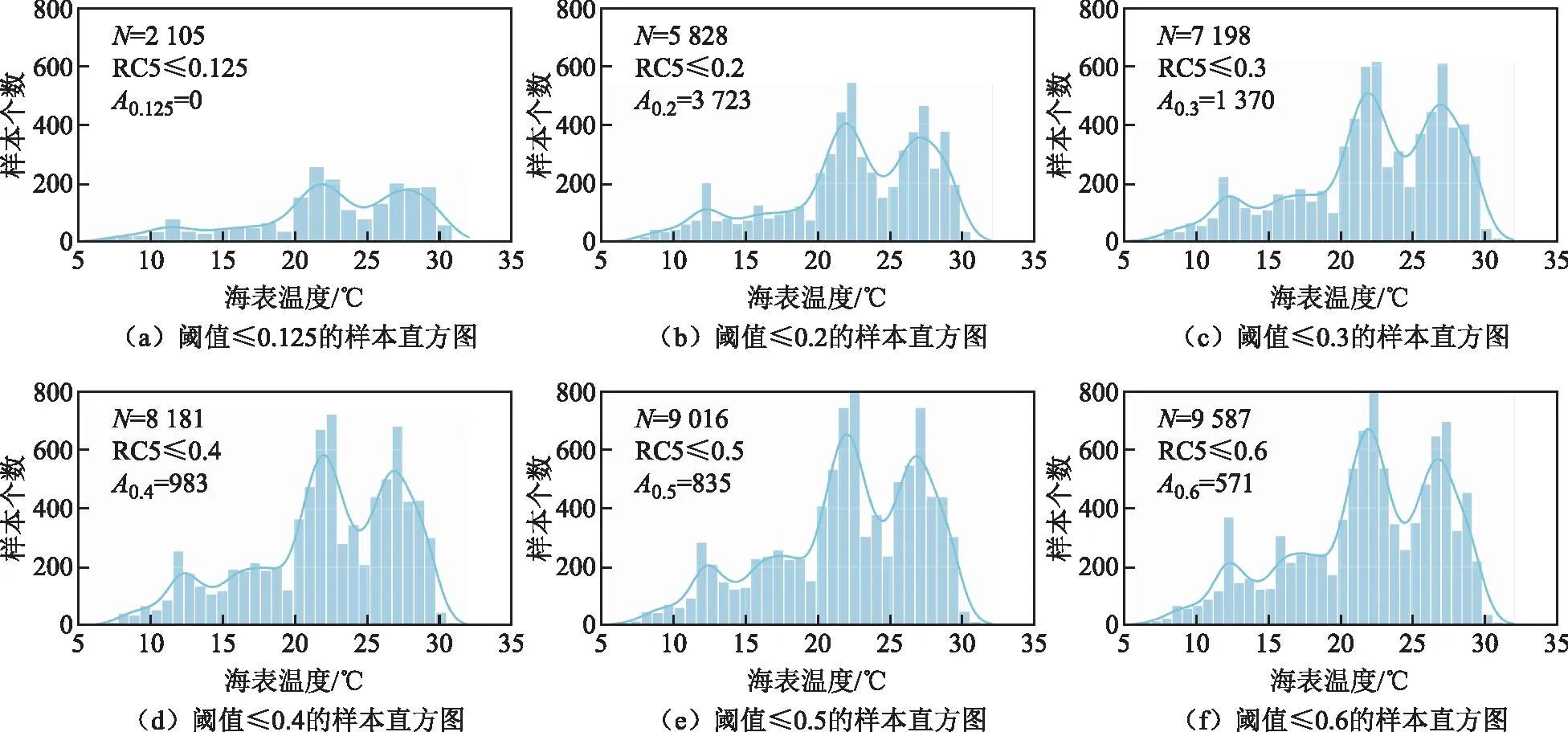
注:RC5表示第5波段瑞利校正值;A表示阈值递增新增样本数量。图3 样本直方图

通过核密度曲线可以发现,每一个样本集合的实测温度分布较为一致。当阈值增加时,在整个温度范围内都有新增样本,使得核密度曲线波峰都维持在4个。

为了准确对比模型在不同阈值下的性能指标,本文将6种阈值样本按照7∶3的比例划分训练和测试样本集。6种阈值下模型在测试数据集上的性能指标如表1所示。在完全无云阈值下(0.125),模型的R2都高于0.98,说明3种模型(MLP、RFR、SVR)在无云情况下具有较高的建模能力。由于0.2阈值条件下可能存在云,因此可以看到当阈值从0.125增到0.2时,模型性能指标都存在不同程度降低。以MLP模型为例,R2从0.98降低到0.93,MAE和RMSE分别从0.4 ℃、0.75 ℃升高到0.74 ℃、1.39 ℃。随着阈值不断增加,3个模型性能指标都不断下降。阈值从0.125到0.4范围内,模型性能下降幅度最大,说明在这个范围内,云类型、云层光学厚度变化较大,每个阈值内的样本差异较大,导致性能急剧下降。3种模型性能指标几乎同时在阈值为0.4以后趋于平稳,说明0.4阈值之后,样本的差异性较低。导致该结果的另一个原因是新增样本数量的减少(A0.5=835,A0.6=571)。其中,SVR模型的性能下降幅度最大,MLP和RFR的变化较为接近。当阈值为0.6时,MLP和RFR的R2同时下降到0.79,SVR的R2下降得更低,为0.74。在MAE指标上,MLP和RFR约为1.5 ℃,SVR则为1.69 ℃。在RMSE指标上,MLP和RFR约为2.4 ℃,SVR约为2.7 ℃。图4展示了不同阈值模型在训练和测试数据集上的性能指标变化折线图。在无云情况下,3个模型的性能指标都高于葵花卫星海表温度产品。整体而言,SVR 3个性能指标普遍低于MLP和RFR。

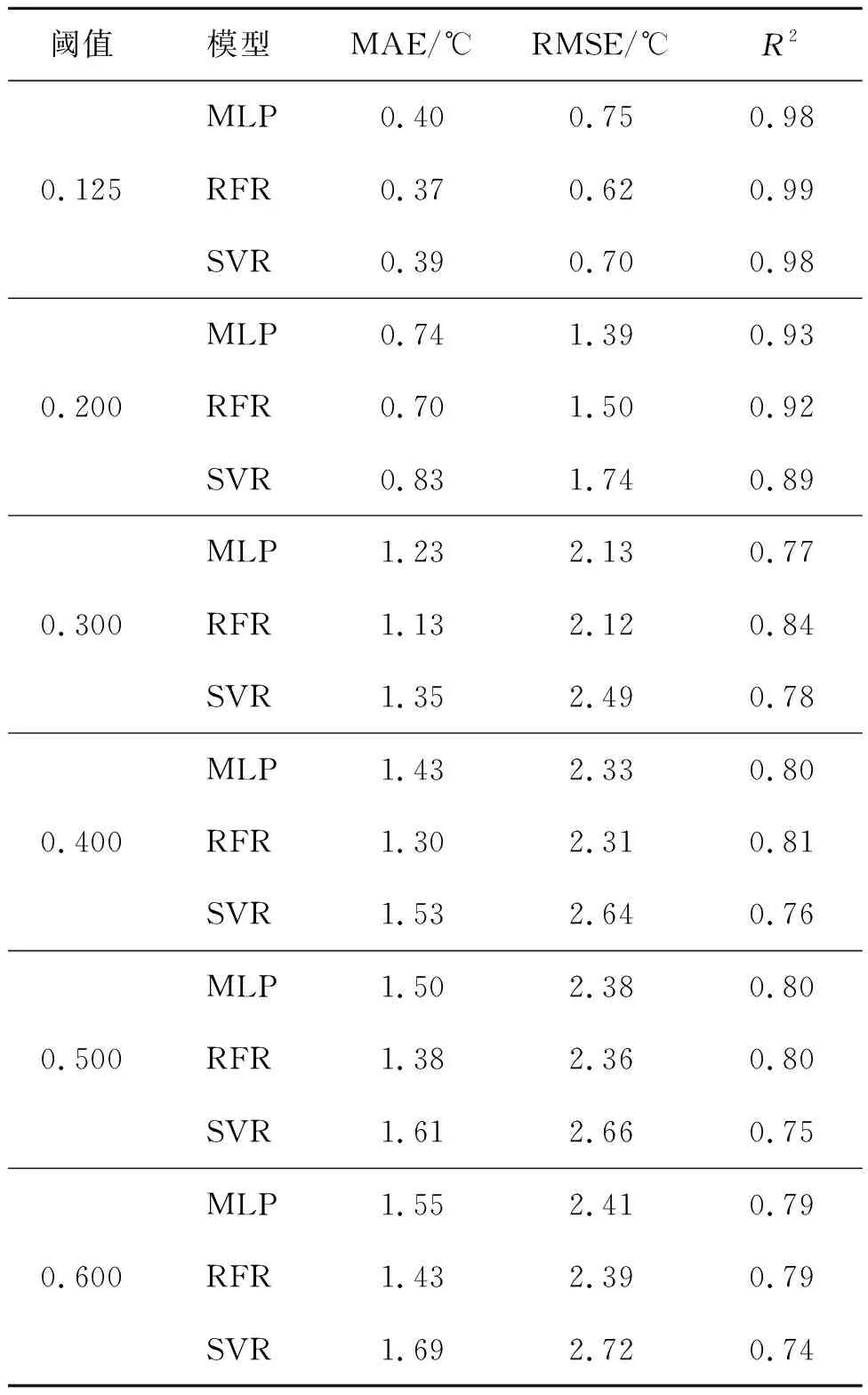
表1 MLP、RFR和SVR模型在不同阈值下的性能指标

注:黑色虚线表示葵花卫星产品在无云情况下的性能。图4 MLP、RFR和SVR模型指标变化图

3.3 不同阈值的模型对无云区域的影响

不同阈值模型需要避免对无云区域影响,确保无云区域反演精度。本文利用不同阈值模型评估无云测试数据(n=632)的性能。利用各个模型差值(预测值-预测值0.125)绘制点图,使用差值的平均值作为中心趋势的估计值,如图5所示。RFR和SVR模型形态较为一致,随着阈值增加,模型对无云区域呈现高估现象。其中RFR模型的影响明显低于SVR,当阈值在[0.3,0.6]范围时,RFR差值的均值保持在0.05 ℃上下,而SVR残差均值则在0.1 ℃左右。MLP模型对无云数据的评估形态有轻微的波动,在阈值为0.2时,预测值相对于0.125阈值模型的预测值具有较大的变化。当阈值在[0.125,0.5]范围时,MLP差值的均值逐渐上升。在阈值为0.6时,出现轻微的下降。随着有云样本数据的加入,3类模型对无云区域的海表温度评估的不确定性不断增加。由于云的遮挡,传感器获得的亮温值会被削弱,当这部分数据被引入到训练样本后,机器学习算法为获得整体最优精度,会加重有云区域的输入特征的权重,从而使得模型在预测无云时出现整体略偏高。

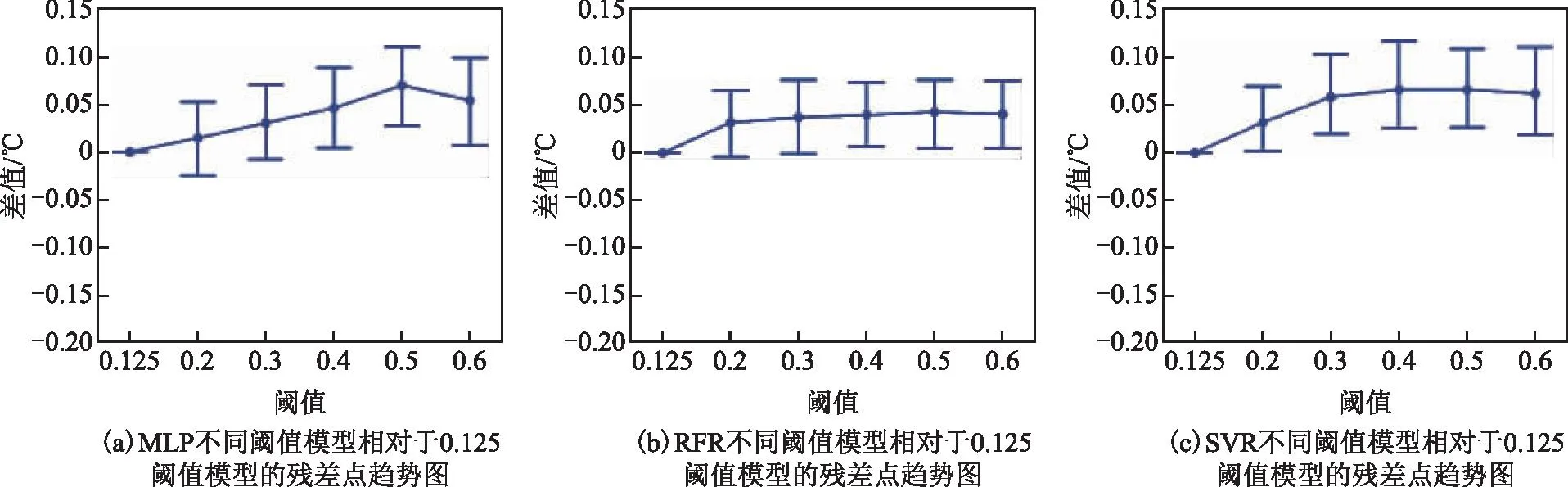
注:圆点为差值的均值;竖线表示95%的置信区间。图5 残差点趋势图

3.4 模型制图能力评估

为了评估阈值模型的可用性,本文进一步分析了阈值模型的制图能力。选取2020年4月10日20°N～30°N,120°E～130°E为制图区域,对该区域Himawari-8卫星L1级数据进行瑞利校正,评估6个阈值模型的制图表现能力,为了展示该区域的海表温度变化,制图过程掩膜了陆地区域。以AHI海表温度产品作为参照,对比分析不同阈值下模型的制图性能和估算准确性,其中为量化模型空间制图比例引入空间覆盖率(spatial coverage percent,SCP)。由于AHI产品无有云区域的海表温度,因此,需要对有云区域模型预估值与实测海表温度进一步进行对比验证。为了增加验证点的数量,实测点与预估值的时间差扩大到±1 h。图6分别是制图区域AHI海表温度产品、制图区域第5波段瑞利校正后的反射率(RC5)和实测点对应像素的RC5。图6中AHI产品缺失的数据与RC5高亮部分具有高度的一致性,说明瑞利反射率判别云层的准确性。实测点中有3个点处于云下区域,4个点为无云区。

图6 海表温度与瑞利反射率

图7展示了各个阈值模型的制图结果及高于该阈值的瑞利校正反射率,表2是7个实测点的葵花海表温度及随阈值递增3种模型预估海表温度值。当阈值为0.125时,3种模型制图结果与葵花海表温度产品相比未表现出明显的差异,表明3种模型在无云区域的预估准确性高,制图结果准确。但仍可以发现RFR相比MLP和SVR具有更多的噪声,主要表现在第6点、第7点周围出现的绿色噪声点(低估现象)。但这些噪声点在0.2阈值以后就消失了,根据图7瑞利校正反射率(RC5)推断是由于只有少量突然升高的瑞利校正反射率样本导致。当0.2阈值及以后样本集包含更多训练样本后,模型在该部分的训练不足得到补偿,从而噪声消失。

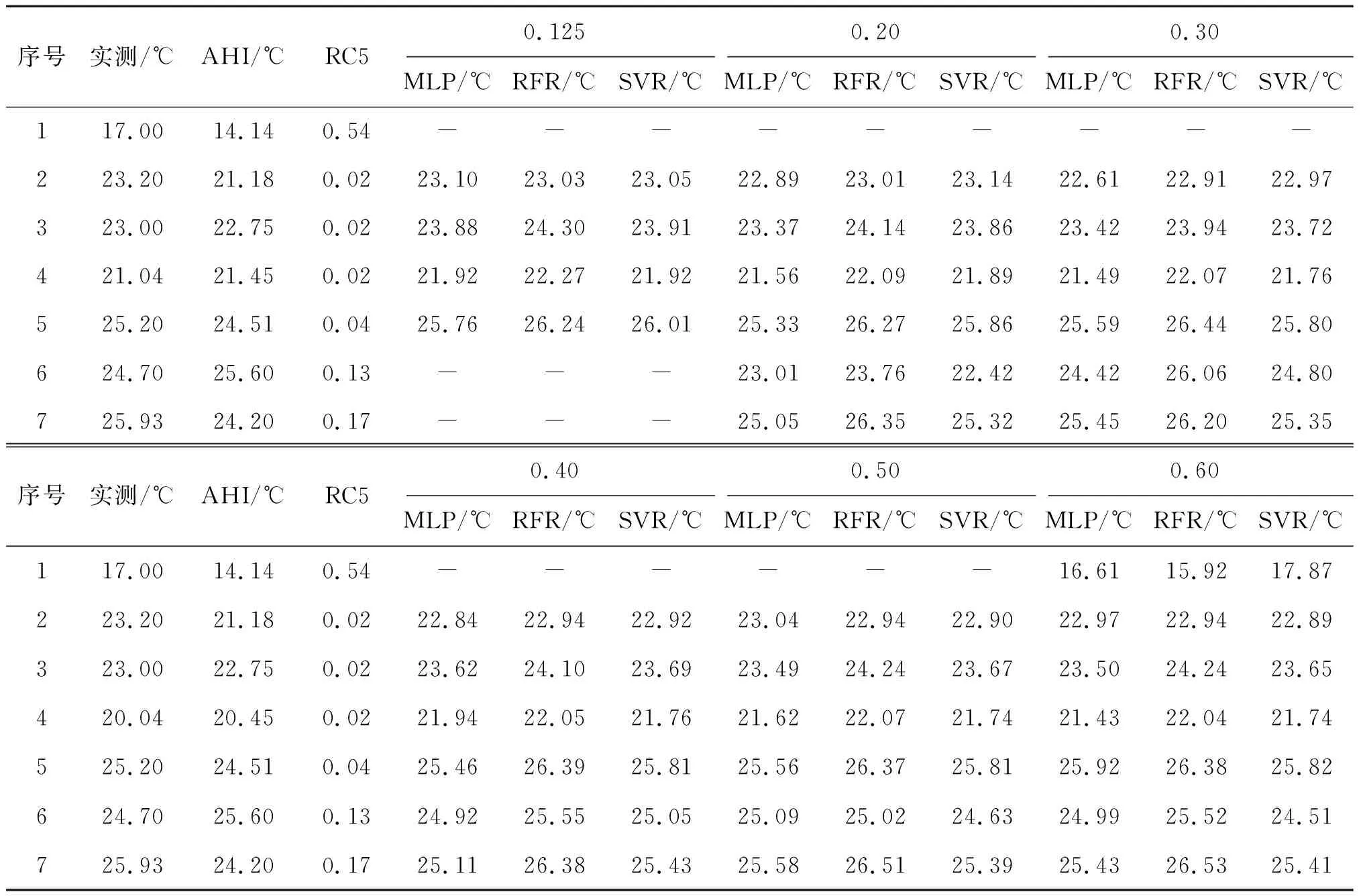
表2 3种算法在6个阈值模型下的预估值

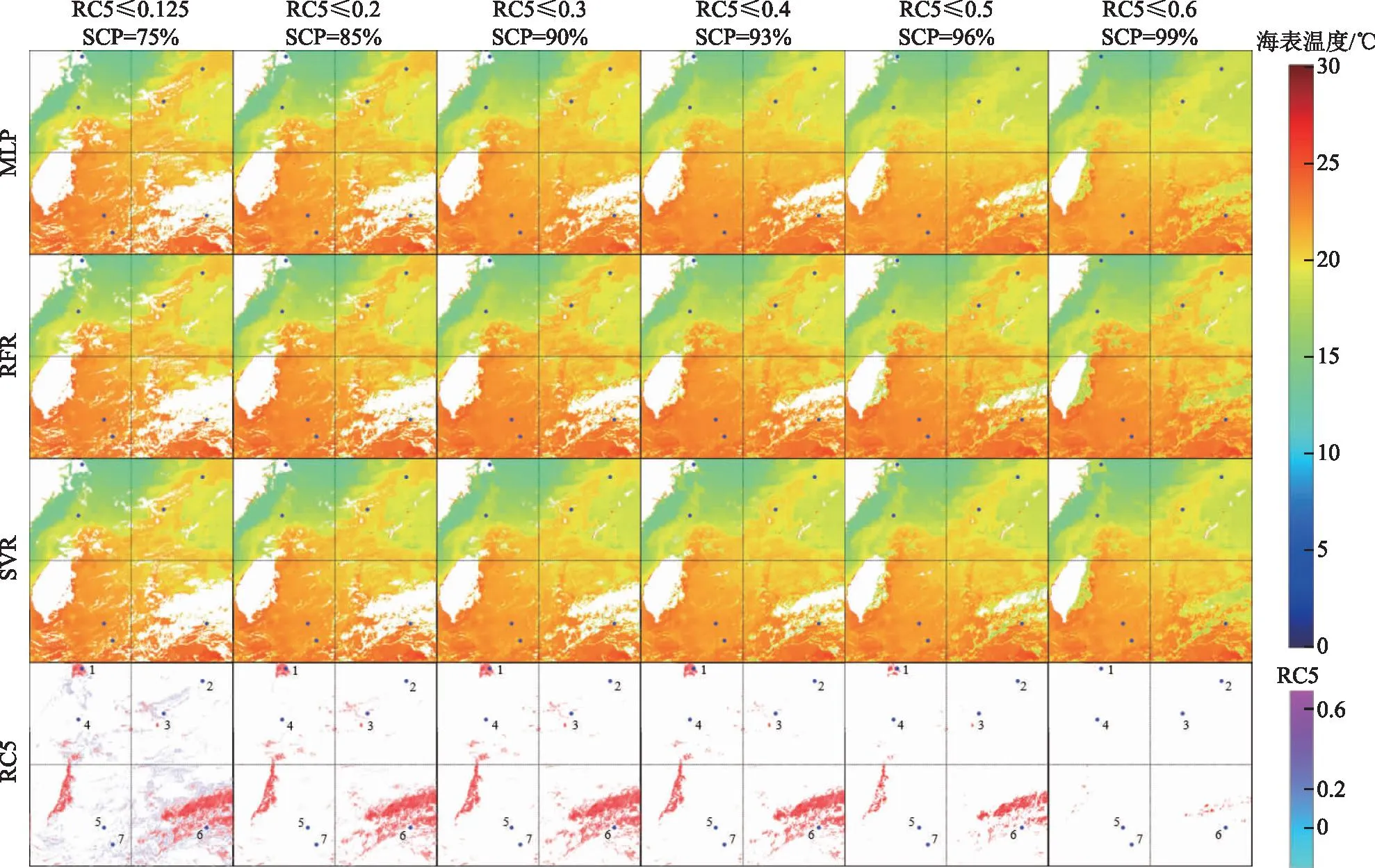
图7 6个阈值条件下MLP、RFR、SVR模型的制图结果,蓝色点为海表温度实测点

当阈值在[0.125,0.3]时,MLP在无云区域预估结果与葵花海表温度产品相比无明显变化。阈值从0.4起,无云区域在制图区域内出现明显的低估现象。不同阈值下RFR在无云区域的预估结果出现略微的高估现象。SVR预估结果在局部区域出现低估现象,该现象主要存在于阈值0.4之后的2号点附近。为验证机器学习模型的制图效果引用平滑性,其中确定平滑性的依据是海表温度的实际分布是随空间逐渐变化平滑过渡的过程,不会发生明显的突变,因此,以此为依据引用平滑性来验证模型的制图效果。不同模型制图效果的平滑性主要在阈值0.4以后的有云区域发生变化,其中6号点附近最为明显。阈值递增至0.3之前,3种模型的平滑性都较好,从0.4开始,不同模型制图效果的平滑性明显降低,递增至0.6时平滑性最差。从整体而言,随着阈值逐渐增大,模型对有云区域的预估准确性和制图效果逐渐降低,空间覆盖率明显增加(从75%增加到99%)。其中阈值0.4是重要的分界线。高于阈值0.4,有云区域的预估结果出现明显低估现象,其中RFR低估现象最为明显,SVR次之。海表温度低估最大值主要出现在阈值0.5以后,表现为海表温度的明显跃迁现象。如我国台湾省东部无云-有云区域的海表温度随着阈值模型发生明显突变,海表温度从25 ℃突然降至20 ℃,造成模型制图结果的平滑性发生明显降低。

3.5 模型敏感性分析

不同的模型在训练期间将对输入特征进行重要性评估,但随着阈值逐渐增大,输入特征重要性的变动及训练效果造成模型的敏感性发生改变。本文基于模型性能指标评估特征重要性(图8)。使用该方法计算第k个阈值数据集,第i个特征的重要性过程如下。

图8 特征重要性

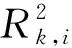
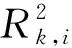
步骤4:按照式(3)计算对第i个特征在所有特征中的权重比例(feature weight,FW),即为重要性,其中n为特征数量。RFR算法在所有阈值模型中,都强依赖于特征BT7。MLP算法对输入特征的敏感性集中于特征RC4、BT12值和D7-14,其余特征在不同阈值的敏感性出现间断性的提升。最明显的是RC4,当阈值大于0.4以后,MLP对该特征的依赖逐渐加重。由于特征RC4是λ=856 nm 为中心波段的瑞利校正值,该波段常被用于判别开放海域是否有云。因此,当阈值不断增加时,该特征的重要性不断增加。该现象同样出现在SVR算法中,在[0.125,0.4]阈值范围内,特征RC5保持一定的重要性,在[0.5,0.6]阈值范围时,RC5重要性减低,但RC4的重要性增加。由于RFR算法中BT7特征的重要性权重太大,由云引起的RC4、RC5特征重要性增加并未出现阈值模型中。

(2)

(3)

4 结束语

本文针对物理算法无法估算云下海表温度的问题,使用机器学习算法构建了阈值海表温度反演模型。通过瑞利校正的短波红外阈值建立6种阈值样本数据集,利用MLP、RFR和SVR算法分别为不同的阈值建立了对应的海表温度反演模型。MLP、RFR和SVR在无云阈值模型中的精度都超过了葵花卫星海表温度产品。整体而言,MLP和RFR算法在各个阈值模型的性能相当,SVR算法性能略差。随着阈值的增大,虽然阈值模型精度有所下降,但增加了海表温度反演的空间覆盖率。3个算法的性能同时在阈值为0.4时趋于平稳,说明本文建立的0.5和0.6阈值的样本有限,无法体现与RC5≤0.4样本的差异性,因此,这两个阈值的性能指标需要增加更多的样本后进一步评估。

虽然3个算法的阈值模型对有云区域出现不同程度的低估,但在无云区域的制图效果与葵花卫星海表温度产品具有较高一致性。海表温度低估最大值主要出现在阈值0.5,因此需要谨慎0.5和0.6阈值模型的应用条件。算法的特征敏感性分析表明,RFR严重依赖BT7特征,这将很可能影响算法泛化能力,在跨地区进行海表温度反演时需重新训练区域性模型。MLP和SVR算法没有出现单一的依赖特征,具有一定的泛化能力。考虑到二者性能的差别,MLP算法进行海表温度反演具有更好的优势。

本文利用不同阈值样本,建立机器学习海表温度反演模型,通过不断提高阈值,可以增加海表温度反演结果的空间覆盖率。本文提出的方法对遥感卫星数据云下海表温度反演具有一定的借鉴意义。考虑到业务化葵花海表温度产品的RMSE约为1 ℃,本文提出的阈值模型有待进一步研究,今后可以通过增加实测数据,与深度学习结合,引入同步微波辐射量以提高云下海表温度反演精度。