相变调控、磁热效应和反常热膨胀*

林源 胡凤霞4)† 沈保根

1)(中国科学院物理研究所,磁学国家重点实验室,北京 100190)

2)(中国科学院宁波材料技术与工程研究所,宁波 315201)

3)(中国科学院大学物理科学学院,北京 100049)

4)(松山湖材料实验室,东莞 523808)

1 引言

相是指各部分化学组成和物理性质完全相同且均匀的宏观物理系统,相变是指物质从一个相向另一个相的转变过程,该过程伴随着物理性质的改变.相变广泛存在于自然界和日常生活之中,例如水的三态变换和蛋白质变性等.相变中因物理性质改变而展现出许多新奇的物理现象,比如晶胞体积或晶格对称性的变化、磁有序度的变化、相变潜热和分子集团构象序的变化等,很早就受到了广泛关注,并且已经被应用于各个领域,如相变制冷、相变储能、相变存储、零热膨胀和负热膨胀材料的制作等.

近些年,相比于传统的汽压缩制冷技术,基于固态相变热效应不断发展起来的固态制冷技术由于具有绿色环保、高效节能、低噪声和容易小型化等优点,引起了广泛关注.这些固态热效应包括由磁场驱动的磁热效应[1–4]、电场驱动的电热效应[5–8]、静水压/单轴力/扭力驱动的机械热效应[9–11].固态制冷技术的核心问题之一在于固态制冷工质热效应的大小,尽可能地提高制冷工质的热效应是固态制冷研究领域长期追求的目标.因此一系列巨热、庞热材料被陆续发现,包括: FeRh[12,13],Gd5Si2Ge2[14,15],La(Fe,Si)13[16]等巨磁热材料;PVDF[5,6],PZT[7],PMN-PT[8]等巨电热材料;Heusler 合金、NiTi 等巨弹热/扭热材料[11,17,18],以及近年发现的塑晶[10]等庞压热材料[19,20].

其中,磁热效应和磁制冷技术是研究历史最悠久的一种.早在1905年,Langevin 证明了顺磁体磁化强度的改变可引起可逆的温度变化.随后,顺磁盐的绝热退磁技术逐步发展成为低温物理学家获得 mK 级超低温的标准手段[21,22].然而,1 mK时多数顺磁离子的磁矩取向被冻结,由于原子核的磁矩仅为顺磁离子的1/1000,因此利用核去磁制冷可以将超低温记录推进到10–6K 以下,这项技术已成为现代低温物理不可缺少的研究手段之一[23].另一方面,利用铁磁体居里温度附近的磁相变可以获得液氦、液氢、室温温区的磁制冷.近年来国际上相继发现的多种新型磁制冷材料大大推动了磁制冷技术的发展,这些材料包括相变温度位于液氦、液氢温区的众多稀土金属间化合物(RT2[24–26],RGa[3,27],RTSi[4],RTAl[4],LiRF4[28]等(R 为稀土元素,T 为过渡族金属元素)),以及室温附近具有磁共结构相变的巨磁热效应材料[12–16].

研究发现,在具有巨热效应的铁性材料体系中,不同铁性序参量间存在强的耦合作用,因而可以在相变附近响应磁场、应力场和电场等多个物理场,进而产生多场调控的耦合热和多卡效应[29].与单场诱导产生的热效应相比,设计合适的多物理场共同作用,会产生更大的热效应、更宽的相变温度窗口以及更大的制冷能力,从而克服单场热效应背后物理机制的固有局限性以及实际应用中存在的缺陷和问题.在这样的研究背景和潜在需求的推动下,多场调控的固态热效应以及多卡效应的研究受到了特别的关注.近期,我们阐明了在巨磁热材料MM'X 基合金(M,M'是过渡族元素,X 是主族元素)和La(Fe,Si)13基化合物中,尽管在从顺磁到铁磁或反铁磁的磁结构相变过程中伴随有晶胞体积的膨胀,该相变的晶格熵变和自旋熵变的符号是一致的[30].在进一步提高热效应方面,通过静水压和磁场的双场调控,先后在La(Fe0.92Co0.08)11.9Si1.1和HoCuSi 化合物中分别将5 T 场下的磁熵变提升到2 倍[31]和1 T 场下的磁熵变提升150%[32].在拓宽相变温区方面,通过恒定电场和磁场双场调控,将PMN-PT 衬底上的FeRh 薄膜的可用制冷温区动态拓宽至60 K (327—387 K)[33].在减小滞后损耗方面,通过使用–6 kV/cm 脉冲电场(诱发的非易失应变)和磁场双场调控,使PMN-PT 衬底上的FeRh 薄膜整个相变温区(310—360 K)内滞后损耗降低了56% 左右[34];并且,为满足实际制冷需求进一步研究了FeRh 磁热材料的循环稳定性[35].依据热力学关系,定量地研究了Ni50Mn35In15合金在静水压和磁场下的耦合热效应,揭示了压力通过增强该类材料中磁-结构耦合强度,导致磁场驱动的相变过程中熵变增强的规律[36].

另一方面,现代工业特别是新兴精密制造业的快速发展迫切需要可以精确控制热膨胀系数甚至零膨胀的材料.研究开发工作温区宽、热膨胀系数可调、性能优异的负热膨胀材料已成为当今凝聚态物理学、材料学的研究热点之一.人们为寻找符合不同工业需求的负膨胀材料付出了诸多努力.一系列具有巨大负热膨胀效应的材料被依次发现,例如ZrWO8系列材料[37],CuO 纳米颗粒[38],(Bi,La)NiO3[39],PbTiO3[40]基化合物,反钙钛矿锰氮化合物[41–46],La(Fe,Co,Si)13[47]和Ca2RuO4[48]等.但这些材料由于有限的负热膨胀系数、窄的工作温区、低的力学性能、低的导电/导热特性等因素,仅有少数能用于实际需要.

具有强磁晶耦合的巨磁热材料体系由磁性原子主导的相变和晶格效应为反常热膨胀材料的研究提供了天然平台.其中,具有Ni2In 型六角结构的三元MM'X (M 和M' 是过渡族元素,X 是主族元素)合金呈现丰富的磁性和马氏相变性质,磁共结构相变伴随大的磁热和压热效应[49–51].通过引入残余应力拓宽相变温区[52],在磁热材料Mn0.97In0.03Co Ge,MnCo0.98Cr0.02Ge,MnCoGe0.99和MnCoGe0.99In0.01体系获得宽温区巨大负热膨胀.进一步地,通过高能球磨控制晶化度和相转变,利用非晶相的自补偿效应在MnCoGe0.99In0.01中实现了超低热膨胀[53],200—310 K (110 K 温跨)的线性热膨胀系数为+6.8×10–7K–1.利用磁场、静水压下的中子衍射研究了掺Fe-MnNiGe 合金磁结构随磁场、静水压、温度的演化规律,揭示自旋序和晶格序的关联关系[54],并利用无公度螺旋磁结构关联的晶格畸变和织构效应获得巨大负热膨胀[55],在195 K (80—275 K)的宽温区范围内,Mn0.87Fe0.13NiGe粘结样品最大线性负热膨胀幅度 ∆L/L∼-23690×10-6,达到其平均晶格贡献(–7121×10–6)的3.3 倍.最近,我们利用中子衍射特有的对相邻Fe,Co 元素的分辨能力,首次确定了La(Fe,Co,Si)13磁热材料的Co 原子占位,并通过电子结构调控获得力学性能优异兼具大磁热效应的超因瓦零膨胀材料,5—250 K 温区的热膨胀系数αl～ 4.5×10–8K–1优于已报道的其他零膨胀材料[56–58].

2 相变调控和磁热效应

2.1 晶格熵变和自旋熵变的符号问题

一级相变巨磁热材料的共同特征是磁相变伴随晶胞参数和/或晶体对称性的不连续变化.铁磁(FM)至顺磁(PM)相变过程中磁无序度增加,自旋熵变ΔSSpin为正值.但是,不同的巨磁热材料在FM 至PM 相变过程中可能会伴随正的[59,60]或负的[2,16,52,61–65]晶格膨胀,晶格熵变符号问题并不明确.磁共结构相变材料的总熵变主要来源于晶格和自旋两部分贡献的加和,如果这两者符号相同,则可以通过增强两者对总熵变的贡献实现热效应的显著增强;相反,两者相互抵消.因此,正确区分晶格和自旋熵变的符号是研究巨磁热材料固态热效应物理机制的重要前提.

然而,对于许多一级相变磁热材料,磁相变和结构相变通常是耦合在一起的,很难将它们完全分离,如Gd5(SixGe1–x)4化合物、MnAs 基化合物和La(Fe,Si)13基化合物.一般而言,较大的晶格体积相由于软的声子振动模具有较大的晶格熵.以具有正膨胀的Gd5(SixGe1–x)4化合物为代表,其磁-结构相变过程是由低温FM 小体积正交结构向高温PM 大体积单斜晶格的相变,FM-PM 相变过程中体积膨胀约为 ∆V/V∼+(0.4%—1.0%)[59,60].PM态的自旋熵大于FM 态的自旋熵.因此,容易理解Gd5(SixGe1–x)4化合物在磁-结构相变过程中的晶格熵变ΔSLatt的符号与自旋熵变ΔSSpin的符号相同.相反,一些巨磁热材料在FM-PM 相变过程伴随负热膨胀行为,即晶格收缩.例如,La(Fe,Si)13基磁热材料在FM-PM 相变过程中尽管晶体结构(空间群:Fm-3c)保持不变,但伴随着显著晶格收缩,体积变化幅度达到 ∆V/V∼–(1.2%—1.6%)[2,16,66].类似地,MnAs 基磁热材料随着温度的升高,经历由大体积FM 六角α-MnAs 相(NiAs 型结构,空间群为P63/mmc)到小体积PM 正交β-MnAs 相(MnP 型结构,空间群为Pnma)的磁-结构相变,伴随的显著的晶格收缩幅度为 ∆V/V∼–(1.1%—2.1%)[62,63].此外,MnCoGe/MnNiGe 基磁热材料在发生从正交TiNiSi 型FM 相向六角Ni2In 型PM相转变过程中伴随 ∆V/V∼–(2.8%—3.9%)异常晶格收缩[52,65,67,68].由于这些材料的铁磁FM 相的晶胞体积大于PM 相的晶胞体积,施加磁场将使材料发生小体积PM 相向大体积FM 相的相变,在这种情况下,通常认为相变过程是自旋熵减小同时晶格熵增大的过程,即晶格和自旋熵变的符号相反.但后期详细的理论和实验研究表明[69–71],晶格熵变的大小和符号取决于发生磁有序相变过程中声子振动模的软化或者强化机制.目前,关于具有负热膨胀特点的巨磁热材料在发生磁-结构/磁弹相变过程中的声子振动模演化机制的实验研究较少,因此这类材料的晶格和自旋熵变的符号相同还是相反一直困扰着人们[70–72].例如,对于负热膨胀MnAs 基磁热材料而言,基于密度泛函理论的研究表明,其晶格熵变对总熵变的贡献与自旋熵变的符号相反[69],但迄今为止尚无直接实验证据予以证实.对于负热膨胀La(Fe,Si)13基磁热材料,Jia 等[72]曾通过理论计算指出,在施加外加磁场时其自旋熵变为负值,而晶格熵变为较小的正值,因此总熵变为负值.以上结果均与研究者们的普遍认识一致.但是最近的实验研究表明,包括La(Fe,Si)13基化合物在内的负热膨胀巨磁热材料的晶格和自旋熵变的符号问题并非如此.Gruner 等[70,71]通过核共振非弹性X 射线散射(nuclear resonant inelastic X-ray scattering,NRIXS)研究了LaFe11.6Si1.4化合物的晶格熵变ΔSLatt,实验结果表明LaFe11.6Si1.4化合物相变过程中具有大小可观的晶格熵变,且与自旋熵变的符号相同.此外,对于磁相变和结构相变分离的正分六角MnCoGe 和MnNiGe 合金而言,尽管合金在经历结构相变时随着温度的升高表现为负热膨胀性质,但是其晶格熵变ΔSLatt和自旋熵变ΔSSpin的符号相同[67,68].笔者课题组郝嘉政等结合前人NRIXS 等相关研究,并利用热流实验和德拜理论计算方法,澄清了具有负热膨胀特点的巨磁热La(Fe,Si)13基化合物和MM'X 合金在磁弹/磁-结构相变过程中晶格熵变和自旋熵变的符号始终相同,符合熵增原理.温度诱导的磁扰动使高能声子峰在顺磁态消失,表明声子在高温小体积顺磁态发生软化,晶格熵增大[71].利用声子态密度计算得到LaFe11.6Si1.3的德拜温度ΘD从铁磁态的ΘD∼363 K降低到顺磁态的ΘD∼348K(图1(a)—(c)),与郝嘉政等[31]根据德拜理论计算得到的La(Fe0.92Co0.08)13的ΘD变化趋势和幅度一致(图1(d)),表明晶格熵增大.这证明La(Fe,Si)13基化合物尽管经历了从大体积铁磁相向小体积顺磁相的相变,但相变过程中晶格熵和自旋熵都是增大的,其符号一致[71,73].

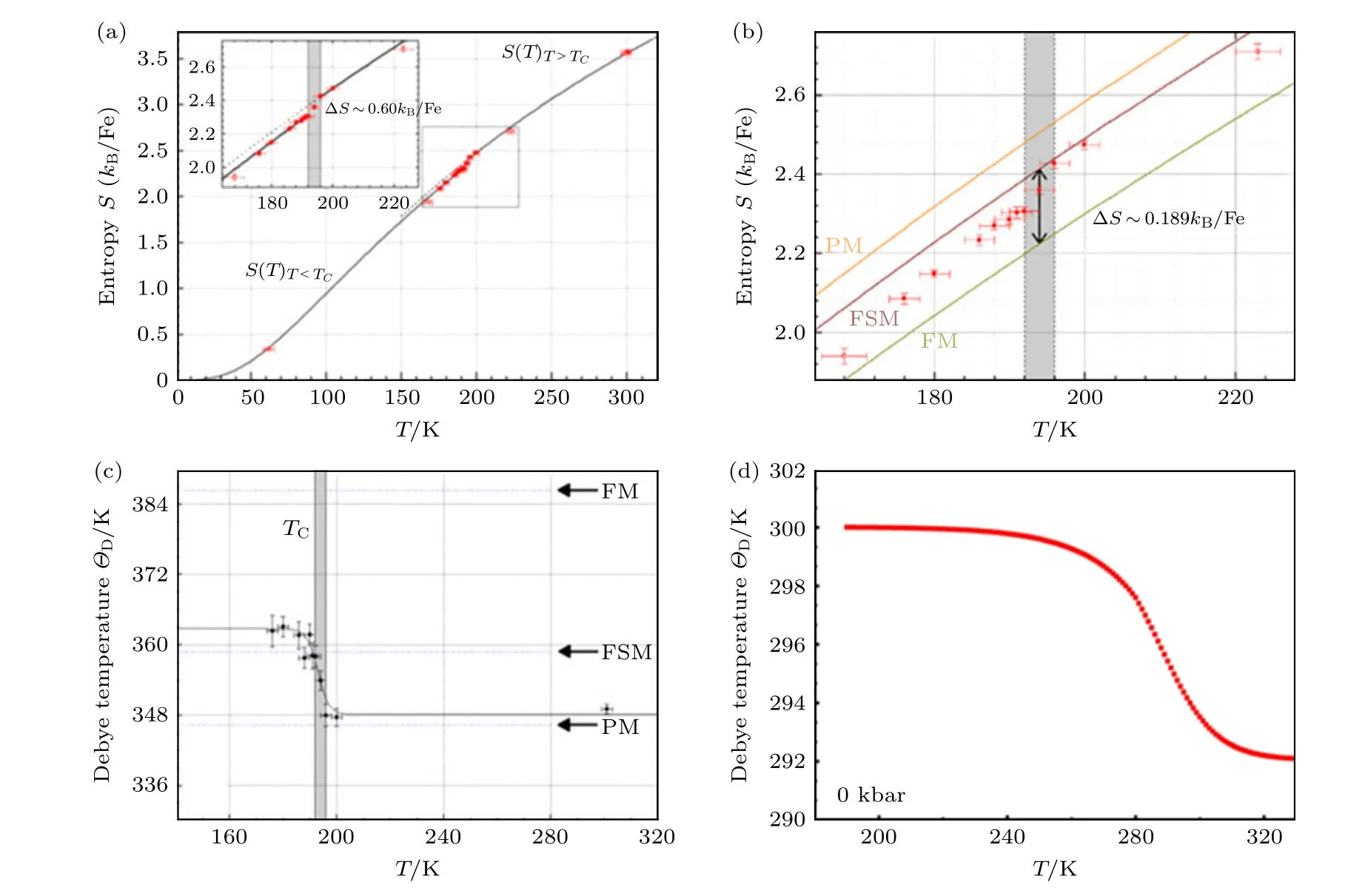
图1 LaFe11.6Si1.3 化合物通过(a)核共振非弹X 射线散射和(b)密度泛函理论计算得到的晶格熵随温度的变化曲线,以及由此得到的(c)德拜温度ΘD 随温度的变化曲线[71];(d)利用德拜近似得到的La(Fe0.92Co0.08)11.9Si1.1 化合物的德拜温度ΘD 随温度的变化曲线[31]Fig.1.Temperature dependence of the experimental (a)and DFT-computed (b)vibrational entropy Slatt (T)of the Fe sublattice for LaFe11.6Si1.4 compound;(c)temperature dependence of the Debye temperature ΘD of the LaFe11.6Si1.4 compound[71];(d)temperature dependence of ΘD for La(Fe0.92Co0.08)11.9Si1.1 calculated using the Debye approximation[31].

2.2 静水压增强的磁热效应

2.2.1 La(Fe0.92Co0.08)11.9Si1.1化合物静水压调控的磁热和压热效应

研究了巨磁热La(Fe0.92Co0.08)11.9Si1.1化合物静水压调控的磁热和压热效应,发现静水压可同时使磁热和压热效应大幅增强.11.3 kbar (1 kbar=100 kPa)压力使磁热熵变增大到2 倍,9 kbar 压力使压热熵变增大到3 倍(图2(a),(b)).利用中子衍射并结合第一性原理计算从原子尺度揭示了压力作用下原子局域环境的改变和相变性质、磁热/压热效应的内在关联[31].

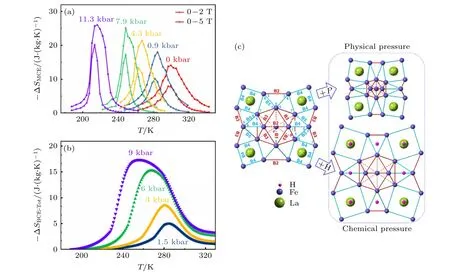
图2 La(Fe0.92Co0.08)11.9Si1.1 化合物在不同压力下(a)磁热熵变 (磁场0—2 T,0—5 T)和(b)压热熵变随温度的变化;(c)物理压力和H 原子引入的化学压力对原子局域环境影响的对比示意图[31]Fig.2.For the La(Fe0.92Co0.08)11.9Si1.1 compound,(a)entropy change for the magnetic field changes of 0–2 T and 0–5 T under different pressures,and (b)entropy change for different pressure changes as a function of temperature;(c)schematic diagram indicating the variations of atomic local environments caused by physical pressure and chemical pressure[31].

NaZn13型立方结构的La(Fe,Si)13基化合物存在5 种Fe—Fe 键长: 二十面体团簇内部和表面的B1,B2,B3 键长以及二十面体团簇之间的B4,B5 键长.原位加压中子粉末衍射结果表明,物理压力通过压缩B1,B2,B3 使二十面体接近等比例收缩,而B4,B5 键长则基本不随压力发生变化(图3).这与La(Fe,Si)13基化合物中引入间隙H 原子所产生的化学压力对原子局域环境的影响显著不同,占据24d 间隙位置H 原子的引入仅影响其近邻的B4 键[74](图2(c)).物理压力使相变性质从二级转变为一级,磁有序伴随的晶胞体积变化显著增大,进而导致显著增强的磁热和压热效应,而H 原子的引入基本不影响相变性质和磁热效应幅度.

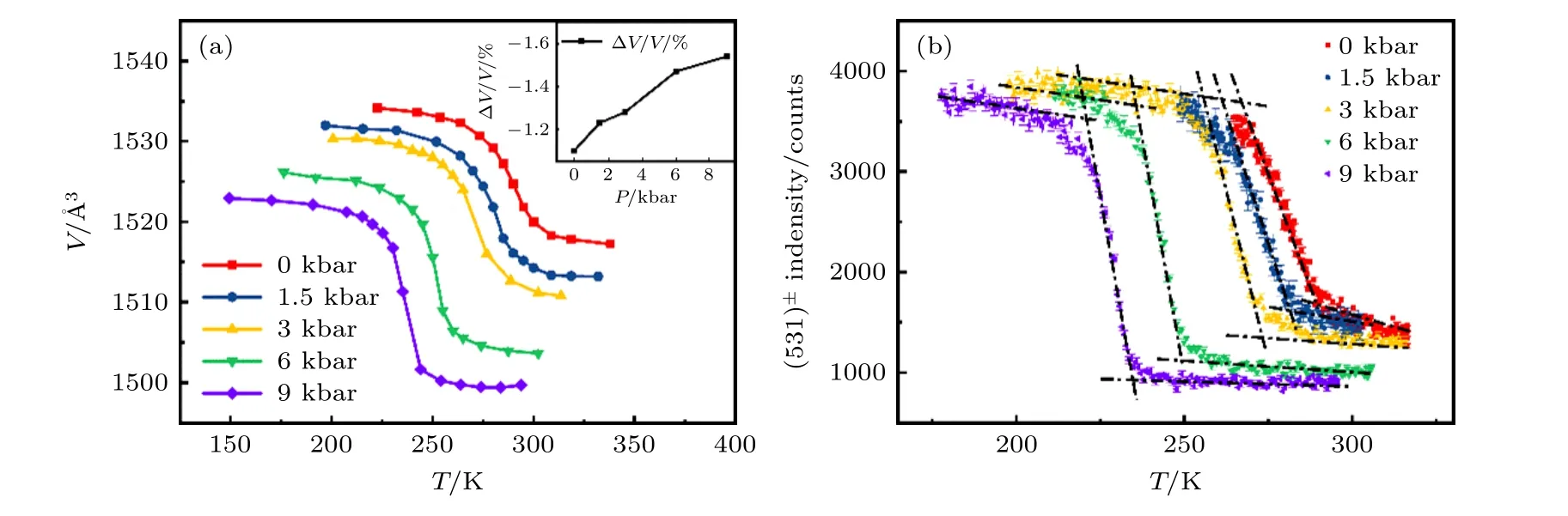
图3 (a)不同物理压力下La(Fe0.92Co0.08)11.9Si1.1 化合物晶胞体积随温度的变化曲线,插图给出了相变过程中相对体积变化ΔV/V 随压力的变化曲线;(b)不同压力下中子衍射(531)±特征峰的峰强计数随温度的变化曲线[31]Fig.3.(a)The lattice volume as a function of temperature for La(Fe0.92Co0.08)11.9Si1.1 compound under different pressures.Inset shows the relative volume change ΔV/V as a function of pressure;(b)neutron intensity (with error bars)of the (531)± reflection as a function of temperature under different pressures[31].

利用第一性原理计算研究La(Fe0.92Co0.08)11.9Si1.1顺磁态的电子态密度随压力的演化规律(图4),并根据朗道相变理论在费米能级处的顺磁态电子态密度定量计算判定相变性质的模-模耦合系数b的数值[61,75].计算结果表明,La(Fe0.92Co0.08)11.9Si1.1化合物在P=0 kbar 时的模-模耦合系数为b∼1.76×10–7,而在P=9 kbar 时化合物的模-模耦合系数为b∼-5.4×10–7,即随着压力的增大,模-模耦合系数b的符号由正变为负,表明物理压力施加使得化合物的相变从二级相变转变为一级相变,进而揭示了物理压力通过引入特殊的晶格畸变以及原子局域环境的变化使La(Fe0.92Co0.08)11.9Si1.1化合物的相变性质从二级转变为一级的物理机制.

图4 0 kbar 和9 kbar 物理压力 下La(Fe0.92Co0.08)11.9Si1.1化合物的顺磁态电子态密度在费米能级处的分布情况;插图给出了0 kbar 和9 kbar 压力下的顺磁态总电子态密度曲线[31]Fig.4.The details of total density of states near the Fermi level EF of La(Fe0.92Co0.08)11.9Si1.1 compound in the nonmagnetic state under pressures 0 and 9 kbar.The inset shows the total DOS in the nonmagnetic state,the Fermi energy is shifted to zero[31].

德拜近似理论定量计算表明,9 kbar 的压力使化合物在相变过程中的晶格熵变ΔSLatt从环境压力下的∼8.9 J/(kg·K)增大到∼12.2 J/(kg·K),增大了37%.这表明相变过程中的晶格熵变随着压力的增大而显著增大.进一步,当压力为9 kbar时,压力诱导的晶格熵变的贡献ΔSBCE-Latt的峰值为∼11.0 J/(kg·K),与1.5 kbar 的晶格熵变相比增大了3 倍.同时,9 kbar 压力下的压热熵变的峰值可达到ΔSBCE-Tot≈17.4 J/(kg·K),这比1.5 kbar压力下的峰值(ΔSBCE-Tot≈5.0 J/(kg·K))大3.48 倍(图2(b)).此外,磁热熵变的计算结果表明当压力从环境压力增大到11.3 kbar 时,磁热熵变的峰值从–14.1 J/(kg·K)增大为–26.0 J/(kg·K)(图2(a)),增加了1.8 倍,并且制冷能力RC 有了13.5% 的提升.制冷能力RC 可由

得到,其中T1和T2分别代表材料等温熵变峰值的半高直线与磁热熵变曲线的两个交点的温度值,ΔSM则为材料等温熵变的峰值.上述结果表明,静水压力通过增强化合物的晶格熵变在总熵变中的贡献来提高La(Fe0.92Co0.08)11.9Si1.1化合物的磁热效应以及压热效应.此外,与前人利用原位压力下的直接测量的压热熵变结果对比发现,我们的计算结果与实验测量的结果具有良好的一致性[76].因此,这项工作提出并验证了一种结合压力下的结构分析技术(如中子衍射、同步辐射)和理论计算获得差式扫描量热仪 (DSC)难以达到的高压力下压热效应的有效方法.

这项工作表明了物理压力通过影响特定原子局域环境获得大幅增强热效应的巨大潜力,对于实现其他与压力相关的新效应(如可控的负热膨胀)也具有重要意义.

2.2.2 HoCuSi 化合物静水压调控的相变和磁热效应

HoCuSi 化合物由于其低温区可逆的巨磁热效应被认为是一种极具应用前景的低温区磁制冷材料[4],其磁热熵变达到33.1 J/(kg·K)(0—5 T),和ErCo2巨磁热材料相比拟[77].我们通过引入静水压调控磁结构和磁化过程,获得了低磁场下大幅增强的巨磁热效应,0—1 T 磁场变化下的熵变和有效制冷能力分别增大150%和134%(6.6 kbar 压力),并且磁化过程保持可逆无滞后[32](图7).HoCuSi在奈尔温度TN∼7 K 以下呈现反铁磁基态(图5),磁结构是Ho3+离子形成的具有传播矢量k=(1/15,0,1/6)的正弦波调制结构,Ho3+离子磁矩为3.3(1)μB,与c轴成61(6)°的夹角,与a轴成132(6)°[78].HoCuSi化合物的复杂非线性的正弦波调制磁结构来源于磁交换以及晶体场作用之间的竞争,表现出对原子局域环境高度敏感[79].研究发现,物理压力的施加影响晶胞参数、稀土Ho3+离子间的距离以及局域环境,从而调制磁结构,表现出铁磁耦合作用的显著增强,居里-外斯定律得到的有效磁矩Meff和顺磁居里温度θP均随压力增大而增大(见图6).6.6 kbar 压力下调制的磁结构在5 K 温度下1 T,2 T 和5 T 磁场时的磁化强度相比于常压分别提高了46%,28% 和11%,但相应的磁结构的磁化过程仍保持可逆无滞后,从而实现了低磁场下可逆磁热效应的大幅增强(见图7).上述结果表明物理压力可以通过调节化合物的晶胞参数以及原子局域环境,调节化合物的非共线磁结构和磁化过程,同时保持磁化过程的可逆性.这项工作发现了一种不同于之前文献报道的通过压力调控磁结构,实现可逆磁热效应显著增强的新机制,对于开发低温区双场驱动的制冷材料和应用具有重要意义.

图5 HoCuSi 化合物正弦波调制的反铁磁基态Fig.5.The AFM ground state of HoCuSi compound with a sin wave modulation spin structure.

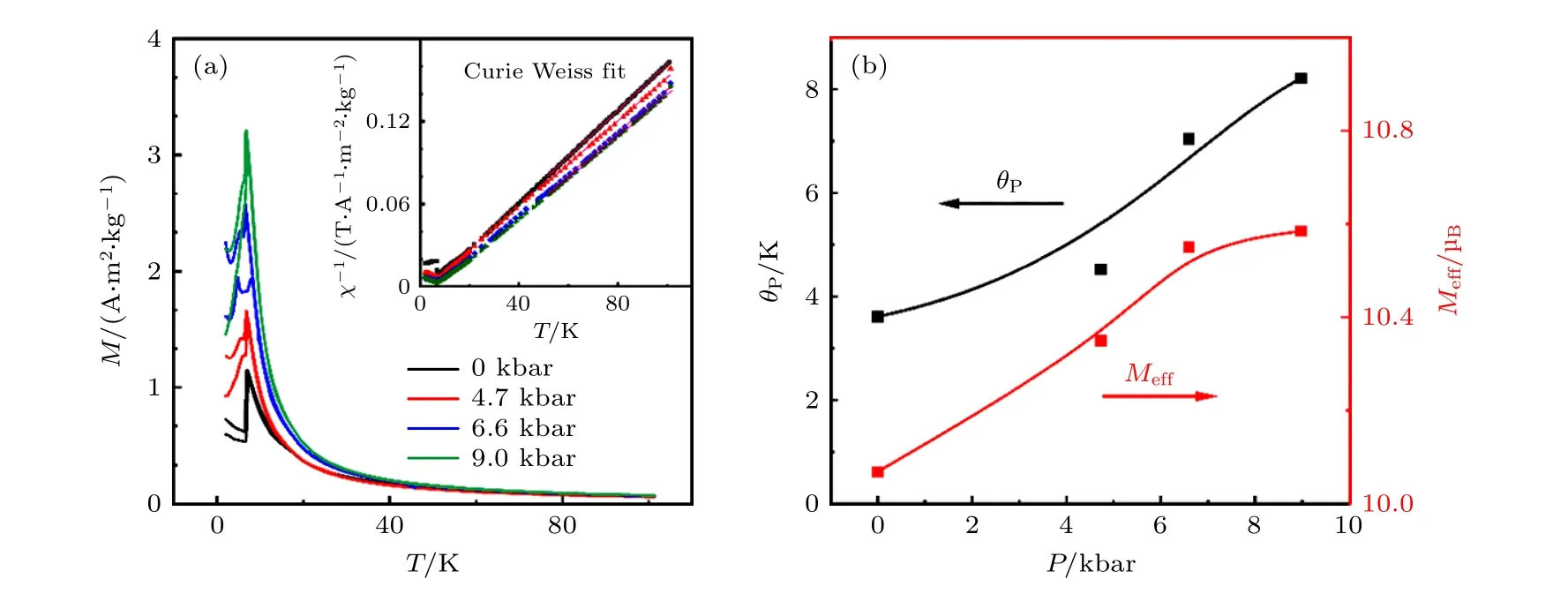
图6 (a)不同物理压力下HoCuSi 化合物在0.01 T 磁场时的升温(ZFC)和降温(FC)过程中的热磁曲线,插图为不同物理压力下的磁化率倒数(1/χ)与温度的关系;(b)基于(a)图中M-T 曲线,根据居里-外斯定律推导得到的有效磁矩Meff 以及顺磁居里温度θP 压力依赖关系[32]Fig.6.(a)Temperature dependences of the ZFC and FC magnetizations for HoCuSi in a magnetic field of 0.01 T under different pressures.The inset shows 1/χ–T curves under different pressures;(b)the pressure dependences of paramagnetic Curie temperature θP and effective magnetic moment Meff derived from the M-T curves in Fig.6(a)[32].

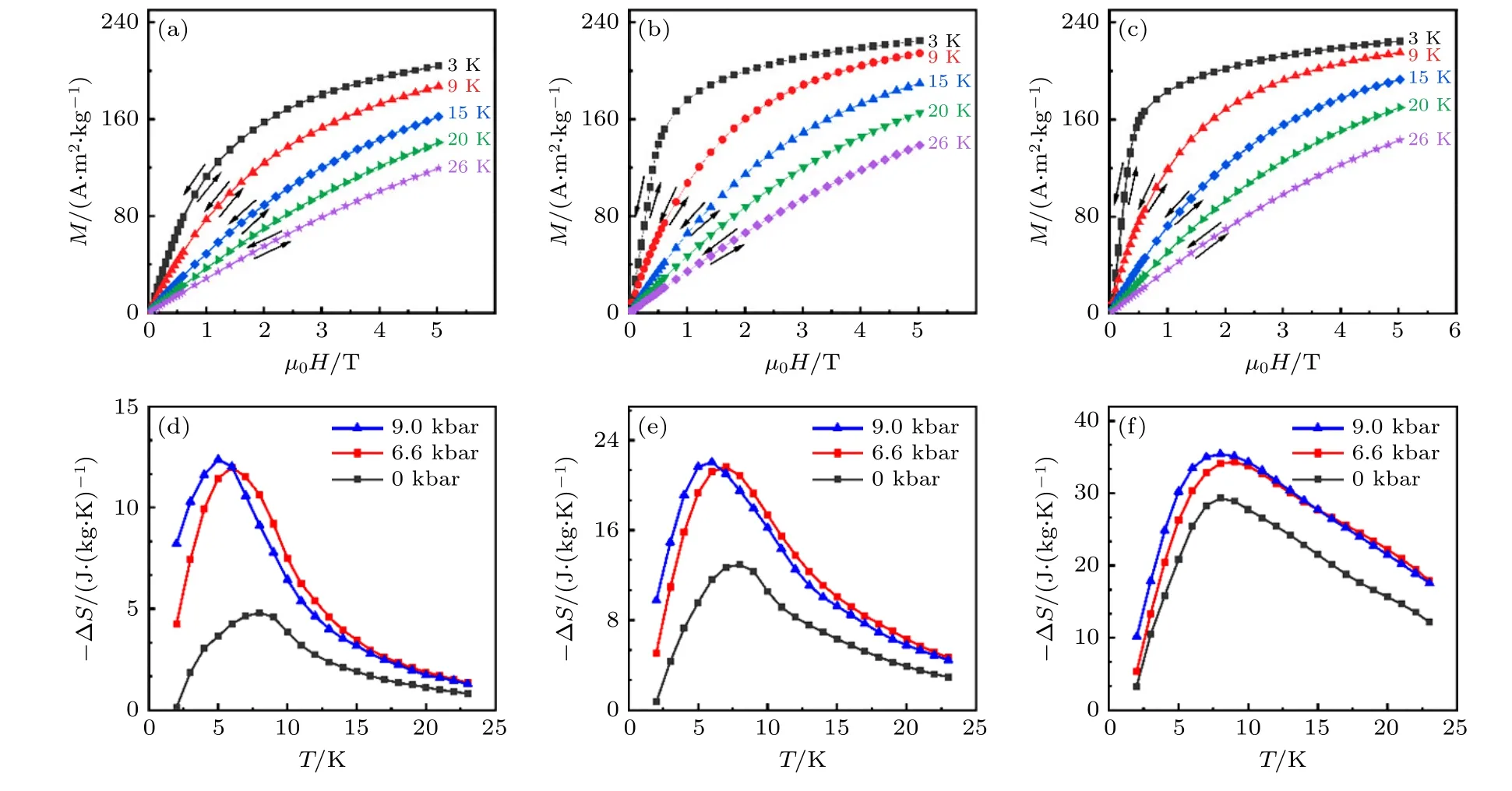
图7 HoCuSi 化合物不同物理压力下相变温度附近的等温磁化曲线 (a)0 kbar,(b)6.6 kbar,(c)9.0 kbar;HoCuSi 化合物在不同磁场变化、不同压力下的磁热熵变随温度的变化曲线 (d)0—1 T,(e)0—2 T,(f)0—5 T[32]Fig.7.Magnetization isotherms of HoCuSi measured on increasing and decreasing fields under (a)0 kbar,(b)6.6 kbar,(c)9.0 kbar,where the arrows indicate the ramping direction of magnetic field;entropy change under different pressures at (d)0–1 T,(e)0–2 T,and (f)0–5 T magnetic field change[32].

2.2.3 PrGa 化合物静水压调控的自旋重取向和磁热效应

PrGa 化合物具有正交CrB 型结构,空间群为Cmcm(#63).根据常压下的中子衍射研究,虽然化合物的晶体结构在整个温度范围内保持晶格对称性不变,但晶胞参数a,b和c均伴随着自旋重取向相变和铁磁相变发生变化[80],结果如图8 所示.随着温度的降低,晶胞参数a单调增大,而b减小(图8(a),(b)).晶胞参数c的情况较为特殊,其在居里温度处出现一个小的突变,而在自旋重取向温度处出现一个更加陡峭的变化,随着温度的降低,晶胞参数c迅速增大.这种行为与化合物自发磁致伸缩密切相关.此外,晶胞参数c对温度的依赖性与化合物沿c轴的磁矩温度依赖性非常相似,如图8(d)所示.说明自旋重取向和磁相变引起的晶格参数的特殊演化规律将导致化合物自旋重取向温度和居里温度对压力具有不同的响应行为.

图8 PrGa 化合物在环境压力下晶胞参数随温度的变化曲线,其中箭头指向自旋重取向温度TSR 和居里温度Tc (a)晶胞参数a;(b)晶胞参数b;(c)晶胞参数c;(d)Pr3+的磁矩沿c 轴(Mc)的投影[81]Fig.8.Temperature dependence of the lattice parameter (a)a,(b)b,(c)c,where the arrows indicate the positions of TSR and Tc;(d)the projection of the magnetic moment along the c axis (Mc)[81].

通过引入压力调控化合物的自旋重取向相变实现了化合物的制冷温区的大幅度拓宽.具有CrB型正交结构的PrGa 的自旋重取向来源于磁交换和晶体场作用之间的竞争[82],其c轴伴随自旋重取向转变发生突变,表现出对物理压力敏感,为研究物理压力调控的自旋重取向和磁热效应提供了平台.研究发现,施加11.4 kbar 的物理压力使自旋重取向温度TSR从28 K 下降到16 K,而居里温度Tc几乎保持不变,进而增大了TSR与Tc之间的温跨(图9).同时,物理压力显著增强了自旋重取向相变的一级相变性质.在11.4 kbar 的压力下,尽管磁热熵变有所降低,但熵变曲线随磁场增大发生不对称展宽,导致磁热熵变曲线呈现平台状,使有效制冷能力提升10%[81](图10).

图9 (a)不同物理压力下PrGa 化 合物在0.5 T 磁场时的升温(ZFC)和降温(FC)过 程中的热磁曲线,其中插图显示了TSR 和Tc 与压力的关系;(b)PrGa 化合物在5 T 磁场下的磁化强度随温度的变化曲线,插图给出了不同压力下的dM/dT 曲线[81]Fig.9.(a)Temperature dependence of the ZFC and the FC magnetization for PrGa under a field 0.5 T,where the inset shows the dependence of TSR and Tc on the application of pressure;(b)temperature dependence magnetization for PrGa under a field 5 T,where the inset shows the corresponding dM/dT curves under different pressures[81].

图10 不同物理压力下PrGa 化合物在磁场变化为0—1 T 和0—5 T 时的等温磁热熵变随温度的变化曲线[81]Fig.10.Temperature dependences of magnetic entropy change under 0 kbar,3.5 kbar,11.4 kbar for the field changes of 0–1 T and 0–5 T,respectively[81].

这项工作表明,可以通过物理压力调控PrGa化合物的多个相变来实现化合物制冷温区的拓宽和有效制冷能力的优化,这对于具有丰富磁相变的重稀土化合物磁热效应的调控具有重要意义.

2.3 PMN-PT/FeRh 异质结电控应变调控的磁热效应

2.3.1 PMN-PT/FeRh 异质结的生长机制

将磁制冷材料薄膜化是制冷器件微型化的发展趋势,然而将薄膜外延/取向生长在与其晶格失配大的衬底上非常困难.根据晶格对应关系定量计算得到立方FeRh 合金与菱方PMN-PT 衬底之间的晶格失配高达5.42% 和25.4%[83,84].通过优化生长条件在不引入缓冲层的情况下成功地在(001)和(011)取向的PMN-PT 衬底上生长出具有良好外延/取向的FeRh 薄膜(图11(a),(b)).利用球差电镜技术(ac-STEM)、电子能量损失谱(EELS)和能量色散X 射线光谱(EDX)等手段揭示了FeRh/PMN-PT 异质结的外延/取向生长机理.HADDF 图像分析表明,在两种取向的PMN-PT 衬底和FeRh薄膜界面处均自然生成了厚度约为4 nm 的尖晶石结构的缓冲层,其取向依赖于PMN-PT 衬底的取向(图11(f)).根据界面处的外延关系,定量计算表明,自然生成的缓冲层使FeRh 薄膜由于晶格失配产生的应变降至0.8% 以下,对于FeRh 薄膜外延生长起着关键性作用.界面处EELS 和EDX 元素分析结果表明,缓冲层中含有衬底中除Pb 元素以外的所有元素,还含有来自薄膜的Fe 元素(图11(g),(h)),由此推断尖晶石结构缓冲层的形成是由于薄膜生长过程中衬底中的Pb 原子挥发,薄膜中的Fe 原子渗入Pb 空位形成的(图11(i)).揭示FeRh薄膜在大失配PMN-PT 基片上的外延生长机理为获得调控的一级相变特性和磁热性能提供了重要基础保障.

图11 FeRh/PMN-PT 异质结XRD 图谱、球差电镜结果及PMN-PT 多畴结构示意图(a)FeRh(011)/(001)PMN-PT 与(b)FeRh(001)/(011)PMN-PT 异质结室温下的XRD 图谱;(c)(001)PMN-PT 单晶多畴结构示意图以及(d)不同铁电畴和FeRh 畴在(001)面内晶胞参数示意图;(e)(011)PMN-PT 单晶多畴结构示意;(f)FeRh(001)/(011)PMN-PT 异质结横截面的球差电镜HAADF图像,标尺是2 nm,右侧展示了相应的α-FeRh、缓冲层和PMN-PT 原子排列示意图;界面附近(g)Fe (绿色)和(h)Pb (蓝色)的EDX元素分布图;(i)界面尖晶石结构缓冲层形成示意图,ABO3 钙钛矿结构的PMN-PT 中Pb (红色原子)挥发,产生空位,与其相邻的原子偏移,薄膜生长过程中界面处Fe 原子渗入基片表面的空位中,形成尖晶石结构的缓冲层[33]Fig.11.The XRD patterns of (a)FeRh(011)/(001)PMN-PT and (b)FeRh(001)/(011)PMN-PT heterostructure at room temperature;(c)configuration of spontaneous polarization vectors along body diagonals shown by arrows for (001)-oriented PMN-PT single crystal and (d)the projections of ferroelectric domains r1/r3 and r2/r4 in the (001)-plane and the corresponding FeRh domains in(011)-plane;(e)configuration of spontaneous polarization vectors along body diagonals shown by arrows for (011)-oriented PMN-PT single crystal;(f)cross-sectional STEM HAADF image of FeRh(001)/(011)PMN-PT heterostructure and the corresponding atomic arrangement of α-FeRh,buffer layer and PMN-PT;EDX mapping of (g)Fe (green)and (h)Pb (blue)element distribution at the interface,where the scale bar is 2 nm in length;(i)schematic diagram of spinel buffer layer formation.Pb atoms (red)in the ABO3 perovskite PMN-PT volatilize at high temperature,and Pb vacancies appear,which give rise to the skewing of adjacent atoms.During film growth,Fe atoms at the interface permeate into Pb vacancies,facilitating the formation of a buffer layer with spinel structure[33].

2.3.2 拓宽相变温区

制冷温区窄是一级相变磁热材料在制冷应用中面临的一大挑战.利用处于菱方R 相的PMNPT 衬底多畴结构特点在FeRh 薄膜中诱导产生具有不同应变的双畴结构,由此使(001)和(011)取向的PMN-PT 衬底上生长的FeRh 薄膜均出现连续的两步相变,从而大幅拓宽制冷温区[33].具体地,对于(011)FeRh/(001)PMN-PT 异质结,利用–8 kV/cm 电场诱导的铁电畴翻转对FeRh 薄膜相变过程进行调控,可使FeRh 薄膜的可用的制冷温区由不加电压时的34 K (327—361 K)拓宽至60 K (327—387 K),增大了将近1 倍.用+8 kV/cm电场诱发的铁电畴翻转,可以使FeRh 薄膜同时应用于两个连续的制冷温区(322—351 K 和361—387 K),最终在不同强度电场的激励下实现了在60 K 宽制冷温区内的磁熵变值和制冷能力连续可调(图12(a)).对于(001)FeRh/(011)PMN-PT 异质结,利用+6 kV/cm 或–6 kV/cm 电场诱发的RO 铁电相变,可以使FeRh 薄膜的两步相变合并,两个磁熵变峰合并为一个峰,磁熵变峰值增大约8%.因此,通过电场调控可以使FeRh 薄膜的制冷能力和磁熵变峰分布或集中在不同的温度区间以满足不同的制冷需求,同时将FeRh 薄膜的可用制冷温区由不加电压时的25 K (331—356 K)拓宽至43 K (331—374 K)(图12(b)).在此基础上设计了电场磁场双场激励的AMR 循环[85](图13).这项工作为利用铁电畴拓宽一级相变材料可用制冷温区,调控磁熵变峰值和制冷能力提供了实验基础.

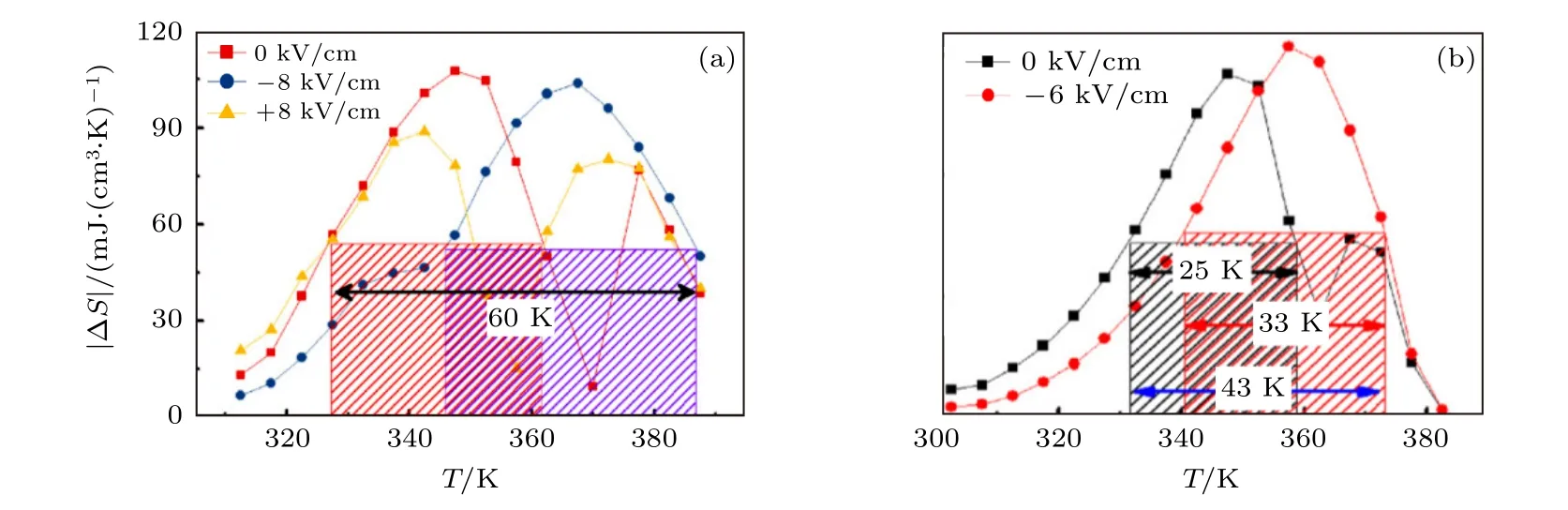
图12 (a)(011)FeRh/(001)PMN-PT 异质结中在电场调控下FeRh 薄膜0—5 T 磁场的磁热熵变随温度的变化;(b)(001)FeRh/(011)PMN-PT 异质结中在电场调控下FeRh 薄膜0—5 T 磁场的磁热熵变随温度的变化[33]Fig.12.The comparison of ΔS curves at 0–5 T under different electric field,where the corresponding refrigeration temperature spans are marked for (a)(011)FeRh/(001)PMN-PT and (b)(001)FeRh/(011)PMN-PT[33].

图13 AMR 循环设计示意图(a)磁场电场双场激励的AMR 循环示意图;(b)通过PMN-PT 基片的铁电畴翻转/相变调控FeRh薄膜的ΔS-T 曲线[33]Fig.13.Schematic diagram of AMR cycle: (a)Schematic diagram of dual field stimulated AMR cycle;(b)the ΔS-T curves of FeRh layer tuning by FE domains of PMN-PT substrates[33].

2.3.3 滞后损耗的非易失性下降

早在1990年FeRh 合金就被发现具有大的磁热效应[12],但是由于大的磁滞后损耗,FeRh 合金很少被考虑用于磁制冷设备.我们通过将铁电PMN-PT 基片在脉冲电场诱导下产生的非易失性应变引入到磁制冷循环,首次实现了FeRh 薄膜磁滞后损耗的非易失性降低[34].

之前的研究中,在多场激励下虽然实现了磁滞后损耗的降低,但是整个退磁过程中需要恒定静水压或恒定电场的引入,限制了双场激励的磁制冷样机的设计[86].我们通过将铁电PMN-PT 基片在脉冲电场诱导下产生的非易失性应变与磁制冷循环相结合(图14(a)),首次实现了FeRh 薄膜磁滞后损耗的非易失性降低(图14(b)).当在5 T 磁场点施加–6 kV/cm 的脉冲电场时,FeRh 合金薄膜在310—360 K 整个相变温区内的非易失性磁滞后损耗的降低比率平均为56%,使FeRh 薄膜有效制冷能力(RCeffe)由68%RC (258 J/kg)提高至86%RC(325 J/kg)(图14(c),(d)).原位电场下的XRD 和RSM 结果证明PMN-PT 铁电基片在脉冲电场下诱发的非易失性应变来源于PMN-PT 基片中的不可逆R-O 相变,在面内[100] 方向非易失性压应变达到了–0.2%[87,88],且该非易失性应变具有循环可重复性.通过定量分析表明,当引入的非易失性应变足够大(>|–0.35%|)时,FeRh 薄膜的磁滞后损耗有望降低为0,甚至变为负值.此时,FeRh 薄膜有效制冷能力(RCeffe)可以通过利用外部机械功提升至100%RC(图14(d)).

薄膜制冷材料与基片的热交换无法避免,引发的漏热问题限制微纳制冷器件的设计与发展.我们通过有限元模拟研究了将不同高热导率材料Cu,Ag,Au,Pt,石墨烯等物质分别作为固态传热介质时薄膜体系里基片的漏热行为(图15(a)).结果表明,影响传热性能的因素不仅与固态传热介质的热导率有关,还依赖于其比热容和密度.模拟结果显示,作为传热介质,Cu 或Ag 的传热效果都优于石墨烯,当选择Cu 为固态换热介质时,基片的漏热仅为0.8%(图15(b)).同时,为了验证模拟结果的有效性,实验上构建了由Cu 层、FeRh 层和PMNPT 基片组成的三明治结构,绝热温变测量结果表明,当Cu 作为传热介质时,PMN-PT 基片的漏热可忽略不计,与有限元模拟结果一致.

图15 FeRh 层向Cu 层和PMN-PT 层热传导示意图(a)以Cu 为传热介质时,有限元模拟得到的Cu 层,FeRh 层和PMNPT 层的温度随时间的变化结果;(b)热量从FeRh 层传导到传热介质(Cu 层)和PMN-PT 基片层的示意图[34]Fig.15.Schematic diagram of heat flow from FeRh to Cu and PMN-PT: (a)Taking Cu as the heat medium,temperature evolution with time indicated by colors for the 3 layers of Cu,FeRh,and PMT-PT based on finite element simulation;(b)schematic diagram of heat flow from FeRh film to the heat transfer medium (Cu)and the PMN-PT substrates[34].

该工作首次提出了制冷循环与非易失性应变相结合的新方法,避免了在磁化和退磁过程中引入恒定电场,从而有效解决了磁制冷样机设计中遇到的双场循环的瓶颈问题.并发现,通过选择合适的换热介质可以有效解决基片的漏热问题,为制冷材料的薄膜化研究提供了实验支撑.

2.4 FeRh 磁热材料的循环稳定性研究

功率密度是衡量磁制冷设备制冷效率的重要参数之一,它与磁制冷材料在循环磁场中的绝热温变值和磁场循环频率有关.研究磁制冷材料的绝热温变在磁场循环中的制冷性能对于其应用具有重要意义.以流体为换热介质的传统AMR 由于对流传热的限制工作频率通常较低,不利于制冷效率的提高[89].全固态磁制冷模型有望解决换热效率低的问题[90].

以FeRh 合金块体为研究对象,利用直接测量手段研究了FeRh 合金的绝热温变ΔTad在磁场循环和温度循环下的稳定性以及频率依赖性质.发现r-FeRh 和α-Fe 第2 相的引入可大幅增强FeRh 磁热效应的循环稳定性(图16(c)—(e))[35].在1.8 T,0.13 Hz 的交变磁场下,ΔTad降低14%,稳定后的绝热温变值为4.1 K,与Gd 单质的绝热温变值5 K (0—2 T)接近,并大幅优于之前报道的单相FeRh 的ΔTad(下降40%—50%)[91](图16(a),(b)).更重要的是,第二相的引入使得反铁磁-铁磁相变能够由较低的磁场驱动.因此,ΔTad在0.62 T,1 Hz 的交变磁场下显著增强,其值高于先前报道的单相FeRh 的70%[92].尽管ΔTad表现出对频率依赖,但在交变 磁场下,当频率从1 Hz 增大到18.4 Hz 时,功率密度增大了11 倍,从0.17 增大到1.9 W/g (图16(f)).基于磁弛豫测量对相变动力学的分析表明,由于FeRh 合金中存在第二相,激活能垒降低,导致驱动场降低[93].这项工作为通过引入第二相提高FeRh 合金中ΔTad在交变磁场下的循环稳定性和低磁场性能提供了一种有效的方法.引入第二相后FeRh 合金的绝热温变虽然随着循环次数的增加有所降低,但是稳定后仍能够与Gd 单质相比拟,且随着频率的增大,FeRh 合金制冷功率密度SCP 逐渐增大.该项研究为FeRh 合金的磁制冷应用提供了直接的实验支持.

图16 (a)373 K,FeRh 合金的温度和交变磁场的强度随时间的变化;(b)373 K,FeRh 合金在1.8 T 磁场820 次循环下绝热温变随时间的变化曲线;(c)α-FeRh 相边界TEM 图像,右上角为选定区域的电子散射图谱;(d),(e)是与(c)相同区域的暗场TEM 图谱,其中(d),(e)分别允许FeRh 和γ-FeRh 散射点通过物镜孔径;(f)不同频率下FeRh 合金的功率密度SCP 随温度的变化曲线,插图为SCP 峰值随频率的依赖曲线[35]Fig.16.(a)Temperature of FeRh alloys and the alternative magnetic field as a function of time at T=373 K;(b)time dependence of adiabatic temperature change ΔT for FeRh alloys at 373 K under 820 cycles of 1.8 T magnetic field;(c)TEM image at the position of phase boundaries for α-FeRh,the inset shows the corresponding selected area electron diffraction (SAED)pattern;(d),(e)dark-field TEM images recorded from the same region as (c),where the diffraction spots of (d)α-FeRh and (e)γ-FeRhare allowed to pass through the hollow objective apertures;(f)temperature dependent SCP curves under different frequency,the inset shows the peak value of SCP as a function of frequency[35].

2.5 多卡和耦合热研究

2.5.1 磁场和压力场作用下多卡效应的热力学描述

磁热效应可以表示为

相应地,压热效应则可以表示为

但是,在某些情况下,熵也可以作为扩展变量的函数,假设S=S(T,M,V),那么,根据麦克斯韦关系,压热效应可以表示为

其中内部的积分项可以分别表示为

对于具有强磁晶耦合的材料,同时施加或者顺序施加磁场和压力场,材料产生的热响应不仅包括零压力下的磁热效应和零磁场下的压热效应,磁晶耦合作用也会在磁场和压力场的共同作用下产生相应的耦合热效应:

磁场和压力场共同作用下总的热效应,即多卡效应,则可以表示为零场压热、零压磁热和耦合热三项的总和[29]:

2.5.2 Ni50Mn35In15合金的耦合热效应

Liang 等[36]在不同压力下磁测量的基础上研究了Heusler 合金Ni50Mn35In15静水压和磁场驱动的耦合热效应.通过连续测量7 个压力下的磁化强度与温度的变化关系,得出磁化强度M与磁场、压力场、温度场 (H,P,T)的对应关系.在5 T磁场下,相变温度区间内,通过tanh 拟合出磁化强度M与压力P关系曲线;在远离相变温区的温度处,通过e 指数函数关系,拟合出磁化强度M与压力P关系曲线.由拟合曲线得到5 T磁场下,磁体积耦合系数与压力以及温度的变化关系,计算出Ni50Mn35In15合金中耦合热ΔScp=的具体表现形式(图17(a)).结果显示,随着压力的增大,耦合热在零压下相变温度处逐渐出现一个大小和位置与原磁热峰相一致的负峰;而在高温区则逐渐出现一个正的峰.通过耦合热对零压下磁热峰的调节作用,耦合热中的负峰的作用主要是抵消掉零压下原磁热峰,而高温处正的磁热峰则表示随着压力的增大,相变被驱动到更高的温度处,在磁场的驱动下,相变在高温处发生并带来熵变.此外,压力的增大虽然会导致其相变前后磁矩值变化量降低,但是由于其一级相变性质增强,所以相变过程中熵变的峰值反而有所增大,在9.95 GPa 压力下,熵变峰值增大8%.对比耦合热对零压下磁热调节后的结果与特定压力下利用Maxwell 关系计算结果可知,压力下磁场驱动相变过程的热效应是耦合热对零压力下磁场驱动相变过程热效应的调节(图17(b)).该研究通过对磁体积耦合系数χ12以及耦合热的定量分析,揭示了压力通过增强该类材料中磁-结构耦合强度,导致磁场驱动的相变过程中熵变增强的规律以及压力拓宽相变温区的本质.

图17 Ni50Mn35In15 合金 (a)耦合热熵变;(b)通过在不同压力下麦克斯韦关系计算得到的多卡熵变(黑色)和通过常压下磁热熵变与耦合热熵变的加和得到的多卡熵变(红色)[36]Fig.17.For Ni50Mn35In15 alloy:(a)Two-dimensional plots of the coupled caloric effect d P d H as a function of pressure and temperature under a magnetic field change of 5–0 T;(b)comparison of the entropy change at ambient pressure adjusted by the coupled effect [S0 GPa(T,5 T–0)+Scp(T,P,5 T–0),black curves] and magnetocaloric results at a specific pressure[S(T,P,5 T–0),red curves] calculated using Maxwell’s relation[36].

3 磁热材料的反常热膨胀

具有Ni2In 型六角结构的三元MM'X 合金体系由于其丰富的磁性和马氏相变性质起了广泛关注[50,94,95],作为MM'X 系列合金家族的成员,正分的MnCoGe,MnNiGe 合金室温分别呈现铁磁性和反铁磁性[94,96],顺磁区域出现无扩散马氏体结构相变: 从高温的Ni2In 型六角结构(空间群:P63/mmc)的奥氏体母相转变为低温的TiNiSi 型(空间群:Pnma)正交结构的马氏体相,正分的MnCoGe,MnNiGe 合金马氏结构相变和磁相变并不重合.但是,这些具有六角结构的三元体系MM'X 中磁交换作用和晶格稳定性均表现出对化学压力敏感.通过引入不同半径、不同价电子数的元素替代Mn(Co,Ni)Ge 中的Mn,Co,Ge,Ni 位,均可调节马氏结构相变(Tstru)和磁相变温度(TC/TN),使Tstru向低温移动.对于合适的组分可以出现磁共结构相变(Tmstru),即磁相变和马氏结构相变同时发生,并观察到了巨大磁热效应[65,95,97].我们[52,53,55]研究了MM'X 合金体系的反常热膨胀,并在RCo2[98]和La(Fe,Co,Si)13磁热材料体系获得近零热膨胀和力学性能优异的超因瓦效应.

3.1 MnCoGe 基合金的负热膨胀

MnCoGe 基合金马氏结构相变过程中均伴随显著负热膨胀,但是一直都没有作为负膨胀材料进行研究.原因是其相变温区窄,力学性能差,材料易碎.利用电弧熔炼技术制备了系列MnCoGe 基合金材料.通过粘结、压制成型引入残余应力的方法改变原子的局域环境,共价键的强度和3d 电子的有效带宽,从而影响材料的磁相变和结构相变过程.引入少量的环氧树脂胶(3%—4%)粘结压片一方面解决了材料易碎的问题,另一方面引入的残余应力有效地拓宽了相变温区(图18(b)).粘结Mn0.97In0.03CoGe,MnCo0.98Cr0.02Ge,MnCoGe0.99和MnCoGe0.99In0.01样品相应的工作温区分别为172 K (58—230 K),210 K (122—332 K),145 K(165—310 K)和108 K(192—310 K),平均负膨胀系数分别为–66.6×10–6/K,–51.5×10–6/K,–71.2×10–6/K 和–94.7×10–6/K[52](图18(c),(d)).其 负膨胀性质超过当时报道的所有其他材料,例如Zr2WO8的平均负热膨胀系数为–9×10–6/K[37].

图18 环氧树脂粘结(a)前和(b)后各粉末样品的M–T 曲线;环氧树脂粘结压片的(c)Mn0.97In0.03CoGe,MnCo0.98Cr0.02Ge,(d)Mn CoGe0.99 和MnCoGe0.99In0.01 粉末样品的线性热膨胀系数[52]Fig.18.Temperature dependence of magnetization under a magnetic field of 0.3 T for (a)as-prepared and (b)bonded samples;temperature dependence of linear thermal expansions ΔL/L for bonded samples with compositions (c)Mn0.97In0.03CoGe,MnCo0.98 Cr0.02Ge,and (d)MnCoGe0.99,MnCoGe0.99In0.01[52].

3.2 MnCoGe0.99In0.01 体系非晶相的自补偿效应导致的超低热膨胀

利用高能球磨改变样品颗粒尺寸、控制晶化度和相转变,在MnCoGe0.99In0.01合金粉末粘结样品中,通过非晶相的自补偿效应实现了超低热膨胀行为[53].高分辨透射电子显微镜图像表明随着颗粒尺寸的减小,样品中开始出现大量的非晶相,大块晶粒也逐渐破碎成充斥缺陷的微粒.其中,颗粒尺寸为0.3—1.0 μm 的小颗粒样品P5 的非晶相比例达到了40%,晶粒的平均尺寸只有8 nm (图19(a)).其中的非晶结构表现为正热膨胀行为,对于材料的负热膨胀性质具有补偿作用.另一方面,中子衍射和X 射线衍射数据的精修结果表明,随着颗粒尺寸的减小,微晶相中越来越多的奥氏体失去了马氏体相变,P5 中失去相变的微晶相占比为55.2%.此外,残余的马氏体相变也随着颗粒尺寸的减小而变得平缓.最终,通过改变样品颗粒尺寸、控制晶化度和相转变的方式,实现了对于MnCoGe0.99In0.01合金粉末样品的负热膨胀性为的连续调控.通过非晶相的自补偿效应和微晶相马氏体相变比例的减少以及相变的变缓,在P5 (0.3—1.0 μm)的粘结样品上实现了200—310 K (110 K 温跨)的线性热膨胀系数为+6.8×10–7K–1的超低热膨胀行为(图19(b)).

图19 MnCoGe0.99In0.01 合金 (a)P5 样品的扫描电子显微镜、高分辨透射电子显微镜和通过傅里叶变换得到的电子散射图像;(b)粘结的粉末样品和块材的线性热膨胀率,颗粒尺寸: P1(10—20 μm),P4(2—5 μm),P3(1—2 μm)和P5(0.3—1.0 μm)[53]Fig.19.For MnCoGe0.99In0.01 alloy: (a)SEM image,high-resolution TEM image,and electron diffraction pattern from Fourier transform,P5 (0.3–1.0 μm),circled regions by the white line indicate the nanocrystallites;(b)linear thermal expansion ∆L/L for the bonded particles compared with the bulk (the reference temperature is 390 K).Particle size: P1 (10–20 μm),P3 (2–5 μm),P4(1–2 μm),and P5 (0.3–1 μm).The inset shows the morphology of the bonded particles[53].

3.3 Mn-Fe-Ni-Ge 体系无公度螺旋磁结构关联的晶格畸变和巨大负热膨胀(NTE)

选择掺Fe 的MnNiGe 基合金,利用中子衍射技术成功解析出其马氏体相呈现无公度圆锥螺旋磁结构,并且随温度下降在150 K 以下演变为一种对压力敏感的摆线型螺旋反铁磁结构(CyS-AFMb),建立了磁相图[54].利用无公度螺旋磁结构关联的晶格畸变和织构效应实现了巨大NTE 行为[55].

前人研究表明,正分MnNiGe 合金的马氏体相呈现无公度平面螺旋反铁磁磁结构[96],在MnNiGe 中引入Fe 会引入Mn-Fe 铁磁耦合并瓦解本征的Mn-Mn 反铁磁(AFM)耦合[65].我们通过与中国散裂中子源(CSNS)以及美国国家标准局(NIST)合作,利用中子衍射技术,对掺Fe的MnNiGe 体系合金中马氏体相的磁结构进行解析.其中,散裂中子源的GPPD 谱仪上收集到的Mn0.89Fe0.11NiGe 合金的中子衍射精修结果表明,其马氏体相的磁矩局限于Mn/Fe 位,表现为一种无公度的圆锥螺旋磁结构(cone-spiral),其螺旋轴沿a轴,磁矩与螺旋轴的夹角为80°,这是GPPD 谱仪成功采集并解析出的首个无公度螺旋磁结构.同期在美国NIST 的BT-1 谱仪上收集的同系列的Mn0.87Fe0.13NiGe 合金中子衍射精修结果表明,其磁结构与Mn0.89Fe0.11NiGe 类似,唯一差异在于其磁矩与螺旋轴的夹角减小为70º.Mn1–xFexNiGe 系列合金的宏观磁测量(M–H曲线)结果表明,随着Fe 掺杂量的增大,饱和磁场单调下降,意味着其磁矩与螺旋轴的夹角将单调减小,这与上述中子精修结果一致(图20).我们利用GPPD 谱仪并与国际上先进的BT-1 谱仪进行中子衍射的对照实验研究,不仅成功解析出了掺Fe 的MnNiGe 体系合金中马氏体相的圆锥螺旋磁结构,更重要的是,这项工作验证了GPPD 中子衍射谱仪的科学有效性与重要价值.

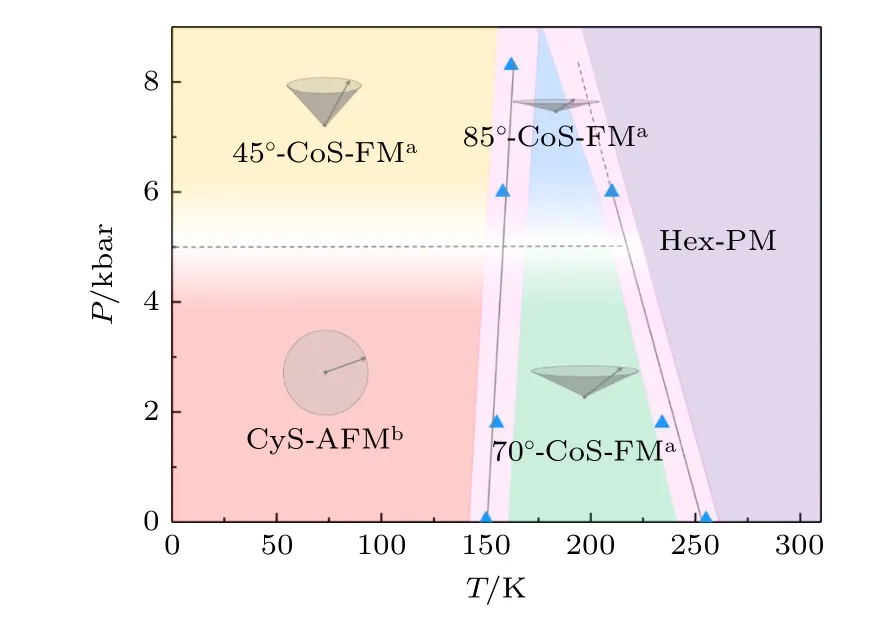
图20 Mn0.87Fe0.13NiGe 合金的磁相图[54]Fig.20.Magnetic phase diagram of Mn0.87Fe0.13NiGe[54].

利用第一性原理计算,研究了Fe 掺杂MnNiGe合金中圆锥螺旋磁结构的稳定性.由于Magmom受限于空间直角坐标系,通常仅能够针对线性磁结构进行计算.我们将螺旋磁结构参数转换到直角坐标系,在Magmom 文件中针对螺旋磁结构建模.为验证其合理性,首先选择正分MnNiGe,计算线性AFM 与平面螺旋AFM 自旋结构的能量.发现两种磁结构都能够收敛,并且在实验值处,平面螺旋AFM 结构的总能量(–78.557 eV/f.u.)低于共线AFM 结构的总能量(–78.272 eV/f.u.),即平面螺旋AFM 结构更加稳定,与实验事实相符.进一步选择Fe 掺杂的Mn0.87Fe0.13NiGe,分别计算其在平面螺旋AFM 与圆锥螺旋磁结构下的能量.结果表明,圆锥螺旋磁结构比平面螺旋AFM 结构的能量低0.8 meV/f.u.,即圆锥螺旋磁结构更加稳定,与中子衍射结果一致[54].

进一步研究发现,无公度圆锥螺旋磁结构的Mn0.87Fe0.13NiGe 与线性铁磁结构的MnCoGe0.99In0.01[99]两种合金马氏相变过程中表现出显著不同的晶格畸变(图21(a),(c)).研究发现,无公度圆锥螺旋磁结构的Mn0.87Fe0.13NiGe 与线性铁磁结构的MnCoGe0.99In0.01的马氏体,由于磁交换作用的不同,二者最近邻Mn—Mn(d1)与次近邻Mn—Mn(d2)的键长差异分别达到了3.61% 与2.60%.相对地,对于顺磁态的六角奥氏体,由于没有磁交换作用的影响,二者的Mn—Mn 键长基本没有差异.这导致在马氏体相变过程中,两种合金表现出不同的晶格各向异性变化.圆锥磁结构的Mn0.87Ni0.13FeGe 合金马氏相变过程中晶格沿六角结构c轴扩展12.01%,而沿着六角结构的a轴收缩9.19%;线性磁结构的MnCoGe0.99In0.01合金的晶格则沿着六角结构的c轴扩展11.3%,而沿着六角结构的a轴收缩6.8%.我们进一步利用

图21 Mn0.87Fe0.13NiGe 合金的(a)磁结构、晶体结构以及(b)负热膨胀行为;MnCoGe0.99In0.01 合金的(c)磁结构、晶体结构以及(d)负热膨胀行为[55]Fig.21.The comparison between the magnetic structure,crystal structure,measured ∆L/L,and the calculated (∆L/L)0=(∆V/V)3 for bonded (a),(b)Mn0.87Fe0.13NiGe and (c),(d)MnCoGe0.99In0.01[55].

定量计算了马氏体相变前后晶格各向异性畸变度∆ani.结果表明圆锥磁结构的Mn0.87Fe0.13NiGe 的晶格畸变度达到∆ani=8.68%,线性磁结构的MnCoGe0.99In0.01的为∆ani=7.49%,前者高于后者15%.

SEM 结果表明,具有更大晶格畸变度的Mn0.87Fe0.13NiGe 粉末颗粒断面出现明显的解理纹路,而MnCoGe0.99In0.01粉末断面上则没有.依据Griffith模型[100]σ=[(2γE)/(πc)]1/2,解理的临界应力σ 正比于解理晶面所需的表面能γ.Mn0.87Fe0.13NiGe合金由于无公度圆锥螺旋磁结构诱导了显著晶格畸变,其晶格内部产生了大量的微裂纹,降低了解理晶面所需的表面能γ,使其相比于MnCoGe0.99In0.01合金更容易发生解理.六角晶格结构中平行于c轴的晶面之间具有相对低的表面能,倾向于沿着c轴方向解理.圆锥磁结构的Mn0.87Fe0.13NiGe合金沿六角结构c轴方向解理,产生可控的织构效应.XRD 结果表明,Mn0.87Fe0.13NiGe 粘结样品表面具有很强的(110)六角晶面的织构效应,即六角结构的c轴方向倾向于躺在面内;相比较,线性磁结构的MnCoGe0.99In0.01合金粘结样品则没有表现出明显的织构效应(图21(d)).晶格畸变和织构效应显著增强了Mn0.87Fe0.13NiGe 粘结合金面内NTE 行为,出现巨大NTE,最大线性负热膨胀幅度达到 ∆L/L∼-23690×10-6,是其平均晶格贡献(–7121×10–6)的3.3 倍(图21(b)).这项工作首次利用无公度螺旋磁结构关联的晶格畸变和织构效应实现巨大NTE 行为,为探索NTE 材料提供了新策略.

3.4 Gdx(Dy0.5Ho0.5)1–xCo2 磁热合金的超低热膨胀

Laves 相金属间化合物RCo2(R 为稀土)由于大的磁热效应(MCE)为人们所熟知[77,101,102].特别是,ErCo2被认为是低温区最具[103]代表性的MCE材料,居里温度TC∼32 K,0—5 T 下的磁熵变高达-∆S∼37.2J/(kg·K)[77].R+3的高磁矩和TC附近大的晶格畸变被认为是巨大MCE 的来源.在RCo2中,Co 亚晶格的磁有序不是本征的,而是由稀土离子的分子场作用所引起[103,104].

例如,当R 位置被非磁性的Y 和Lu 离子填充时,交换增强的泡利顺磁性在样品中占主导地位[104].相反,当磁性稀土元素占据R 位时,4f 和3d 电子间的交换相互作用诱导Co 磁矩.对于重稀土(Gd,Tb,Dy,Ho,Er),R 和Co 之间的交换耦合导致亚铁磁性(FIM),而轻稀土元素导致铁磁性(FM)[103].ErCo2,HoCo2和DyCo2在居里温度附近表现出一级相变和大的磁体积效应,从FIM 到顺磁(PM)的磁相变伴随反常晶格收缩[77,105,106].随着R 元素序数的增加,一级相变性质和晶格畸变度均逐渐减弱.对于TbCo2和GdCo2,理论和实验研究都证明TC附近呈现二级相变并具有可忽略的晶格畸变[107,108].通过在Co 的位置引入Fe,Si,Al 等元素影响交换作用、调控相变温度和相变过程获得了宽温区的反常热膨胀[109–112].

我们希望通过稀土R 位的适当混合调节磁体积效应并实现超低热膨胀.我们制备了Gdx(Dy0.5Ho0.5)1–xCo2(x=0,0.1,0.3,0.5)化合物,通过调节Gd 浓度实现了宽温区的超低热膨胀[98].在低Gd含量x=0,0.1 时,由于在磁结构转变过程中的显著晶格贡献,材料表现出大的MCE (图22).而对于x=0.3,0.5,FIM 区域出现超低热膨胀(图23(e),(f)),其原因归因于FIM 区的磁体积效应和非谐晶格振动之间的平衡,其中R 离子在菱方FIM 相中沿c轴的排列在调节磁致伸缩过程中起着主导作用.此外,对于x=0.5,由于Gd 掺杂抑制了晶格畸变,在TC周围的相变区也发生了超低热膨胀(图23(e),(f)).连续温区(5—280 K)的热膨胀系数CTEsαl∼+1.3×10-6K–1(5—220 K),–1.5×10–6K–1(220—280 K)均优于因瓦合金Fe0.65Ni0.35(αl∼1.5×10-6K–1,193—373 K,∆T∼180 K),

图22 Gdx(Ho0.5Dy0.5)1–xCo2 合金体系的不同组分(x=0,0.1,0.3,0.5)在(a)0—2 T 和(b)0—5 T 磁场下的磁熵变随温度的变化[98]Fig.22.For Gdx(Ho0.5Dy0.5)1–xCo2 compounds,entropy change ΔS under (a)0–2 T and (b)0–5 T magnetic field change for the samples with various Gd contents,x=0,0.1,0.3,0.5[98].

图23 Gdx(Dy0.5Ho0.5)1–xCo2 合金体系(a)菱方亚铁磁结构和(b)立方顺磁结构的示意图,其中箭头方向表示磁矩的方向;该体系(c)x=0 和(d)x=0.5 的组分的变温XRD 图谱,该体系x=0,0.3,0.5 的组分的晶格体积(e)和晶格参数(f)随温度的变化,其中线性热系数αl 和相应的操作间隔ΔT 已标记[98]Fig.23.The sketches of (a)rhombohedral FIM and (b)cubic PM structure of Gdx(Dy0.5Ho0.5)1–xCo2 compounds.Arrows indicate the directions of magnetic moments.The variable temperature XRD patterns around the cubic (311)and (222)peaks of Gdx(Ho0.5Dy0.5)1–xCo2 for (c)x=0 and (d)x=0.5,where the blue balls marked on the peaks’ top and the lines guide eyes.Temperature dependence of (e)the lattice volume and (f)the lattice parameters for x=0,0.3,0.5,where the linear thermal coefficients αl and the corresponding operation intervals ΔT are marked[98].

并且通过线性拟合粗略估计的平均CTE 可以低至αl∼+6.9×10-7K–1(5—280 K)(图23(e)).这项工作为探索超低热膨胀材料提供了新思路.

3.5 LaFe11.6–xCoxSi1.4 磁热材料的电子结构调控和因瓦效应

通过电子结构调控,我们在LaFe11.6–xCoxSi1.4磁热材料中实现了具有优异力学性能的因瓦效应[113].线膨胀系数(αl∼1.5×10-8K–1,5—250 K)优于大多数已报道的零热膨胀材料,包括著名的因瓦合金Fe0.65Ni0.35[56–58].利用中子衍射对Fe,Co相邻元素的独特分辨能力,确定了Co 原子的位置占有率.在此基础上,利用第一性原理计算研究了原子分辨的电子结构.Co 原子的引入增加了3d 成键电子数,从而改变了电子转移特性,导致自发磁致伸缩被抑制,在LaFe10.6Co1.0Si1.4的铁磁区域出现超因瓦效应.电子局域函数(ELF)计算证实了Fe—Co键合强度的提高和优异力学性能的来源.测得的抗压强度达到～340 MPa,这赋予了LaFe10.6Co1.0Si1.4良好的加工能力.此外,根据态密度(DOS)计算的模模耦合系数b解释了Co 掺杂引起的相变性质的演变.这项工作从电子结构调制的角度为开发La(Fe,Co,Si)13合金的多功能应用提供了基础.

4 总结与展望

固态制冷技术因具有环保、高效、低噪和易小型化等优点被视为替代汽压缩制冷技术的理想选择之一.本文介绍了我们近期利用多场调控在增大磁熵变幅度、拓宽工作温区和减小滞后损耗等方面取得的系列进展.目前的研究大多集中于压力、磁场的双场调控,利用压力、电场以及电场、磁场对铁性材料的相变调控仍需进一步研究.此外,对于耦合热和多卡效应的理论和实验研究仍不足: 不同体系深层次的物理机理有待深入;实验研究尚处于初级阶段.从目前已有的压力、磁场双场调控所取得的成就来看,多卡效应的研究还有很大空间.目前已有的固态制冷器件绝大部分都是基于单场调控的单卡效应,适用于多场调控的多卡效应的制冷器件的设计和制作踏足不够,利用多卡效应的新型固态制冷器件极有可能具有更高的制冷效率和制冷功率,期待人们去探索.另一方面,反常热膨胀(零热膨胀、负热膨胀)材料在精密制造业具有重要应用,具有强磁晶耦合的巨磁热材料体系由磁性原子主导的相变和晶格效应为反常热膨胀材料的研究提供了天然平台,但目前人们仅探索了MM'X,RCo2和La(Fe,Si)13典型磁热体系的反常热膨胀行为.众多磁热材料表现出强的磁晶耦合特性,具有探索宽温域反常热膨胀性质的巨大潜力,并且其热膨胀系数和温域具有磁场可调控的特点.广泛深入的材料研究不仅有利于机理探索,而且对于设计具有多功能物性的实用型相变材料具有重要指导意义.