二维莫尔超晶格中的非线性霍尔效应*

吴泽飞 黄美珍 王宁

1)(香港科技大学物理系,香港 999077)

2)(曼彻斯特大学物理与天文系及英国国家石墨烯中心,曼彻斯特 M13 9PL,英国)

1 引言

霍尔效应是指在平行方向施加电流时在垂直于电流方向产生电压的现象.自1879年发现以来[1],霍尔效应家族已经成为一个庞大的群体[2–7],对其进行深入的研究是现今凝聚态物理学领域的重要课题.新近发现的非线性霍尔效应是霍尔效应家族的新成员[8–15].与以往大部分霍尔效应不同的是,非线性霍尔效应不需要打破系统的时间反演对称性,而需要打破空间反演对称性.自2015年以来,非线性霍尔效应被预测并证实存在于少数能带中贝里曲率不均匀分布的材料中.具体来说,当在材料中施加纵向交流电场时,会在横向产生与注入电流二次方成正比的霍尔电信号.这个霍尔电信号包含两个成分: 一个是以注入电流两倍频率振荡的横向电压,另一个是由注入电流转换而来的直流信号.随着实验数据的积累和理论分析的深入,人们意识到非线性霍尔效应的产生机制大概可以分为内禀和散射两类: 内禀机制由贝里曲率偶极矩导致,理论上可以在一些具有倾斜能带结构的量子材料和第二类半金属材料中实现[8];散射机制的产生原因比较复杂,现阶段还难以实现有效调控[16].尽管非线性霍尔效应的发现仅仅数年,其在无线通信、能量收集和红外探测器等领域广泛的应用前景却已被普遍认可.主要原因在于非线性霍尔效应中电信号的倍频和整流是通过材料的固有量子特性——贝里曲率偶极矩决定的,不具有传统电子器件中的电压阈值或过渡时间限制[17–19].然而,贝里曲率偶极矩的存在对体系的晶格对称性除了空间反演破缺外还有更严格的要求,可供选择的材料十分有限.这大大降低了人们优化非线性霍尔效应信号大小的能力,限制了非线性霍尔效应的应用与发展.

近年来,快速发展的范德瓦耳斯堆叠技术为设计、剪裁和调控晶格的对称性,制备具有特殊物理性质的人工莫尔晶体提供了一个崭新的途径.二维莫尔超晶格的出现吸引了大批学者的目光.最近,对石墨烯超晶格[20–29]以及过渡金属硫族化合物超晶格[30–33]的理论和实验研究已经表明,人工莫尔超晶格材料相比天然非莫尔晶体具有更大的贝里曲率偶极矩,在产生和调控非线性霍尔效应方面具有明显的优势.另一方面,人们在二维超晶格材料中观测到了丰富的强关联效应,譬如非常规超导[34,35]、关联绝缘态[36,37]、金属-绝缘态二阶相变[30,38,39]等.研究这些效应与非线性霍尔效应的关联可以加深对非线性霍尔效应的认识.此外,是否可以利用非线性霍尔效应去更好地研究以上这些量子关联态,是一个方兴未艾的研究方向.简而言之,对二维莫尔超晶格中非线性霍尔效应的研究不仅可以使人们对材料贝里曲率的动量空间分布有新的认识,对实现更稳定的拓扑输运、关联绝缘态和超流体非常重要,还极大地拓展了莫尔超晶格材料的功能空间,对设计新型电子和光电器件具有重要的意义.

本文首先介绍非线性霍尔效应的诞生和发展,讨论贝里曲率偶极矩和无序散射这两种非线性霍尔效应的产生机制、区分方式以及在非莫尔超晶格材料当中非线性霍尔效应的实现.随后,介绍二维莫尔超晶格在实现和探索非线性霍尔效应方面具有的四点特性: 可观的贝里曲率,对称性破缺,强关联效应和可调控的能带结构.接下来,回顾并总结石墨烯超晶格以及过渡金属硫族化合物超晶格中非线性霍尔效应的理论和实验进展.最后,对未来基于莫尔超晶格材料的非线性霍尔效应的研究方向和潜在应用进行展望.

2 非线性霍尔效应的诞生和发展

2.1 贝里曲率偶极矩导致的非线性霍尔效应

霍尔效应是指载流子纵向运动时产生横向电压的现象.线性霍尔效应中,霍尔电导正比于贝里曲率的积分.贝里曲率在空间反演下不变,在时间反演下变号[40].因此,在有时间反演的系统中,积分时正动量和负动量的部分会抵消,霍尔电导为零.需要通过外加磁场或材料内部磁化打破时间反演对称性来实现非零霍尔电导[41–44].

2015年,Sodemann 和Fu[8]提出一 种在时间反演不变的系统中仍然可以出现的霍尔效应——非线性霍尔效应.他们在电子分布函数中添加二阶非线性项后求解玻尔兹曼输运方程,发现纵向交流电场可以在横向产生零倍频(直流)和二倍频的电信号.产生的直流和二倍频电流密度分别为,其中ε是沿下标方向的外加电场的振幅,非线性系数可以写为

其中εadc是Levi-Civita 符号,ω是纵向电场频率,τ是弛豫时间,Ωd是贝里曲率,f0是费米分布.这时,定义贝里曲率偶极矩为

则可以得到非线性霍尔信号正比于贝里曲率偶极矩的结论.观察(2)式,可以发现贝里曲率偶极矩是对费米面下所有贝里曲率的一阶导数积分,也就是说,非线性霍尔效应是贝里曲率的高阶效应,所以是新物理.

利用分部积分,还可以得到贝里曲率偶极矩的另一种表达形式:

也就是费米面上的群速度乘以贝里曲率的积分.利用(3)式,可以分析产生非线性霍尔效应的条件.

首先,在时间反演下,群速度和贝里曲率都反号,它们的乘积不变号,说明有时间反演的时候也可以观测到非线性霍尔效应.其次,在空间反演下,群速度反号,贝里曲率不反号,它们的乘积反号,因此积分的时候正动量和负动量的部分会抵消,贝里曲率偶极矩为零.如果想观察到非线性霍尔效应,必须破坏空间反演对称性.此外,通过分析贝里曲率偶极矩在不同对称性操作下的变化,可以找到允许非零非线性霍尔信号的晶体点群结构[45].对于三维晶体,非零贝里曲率偶极矩可以在18 种回旋点群[46]中存在.对于二维材料,要想有非零贝里曲率偶极矩,材料至多只能存在一条镜面对称轴.根据材料的对称性和贝里曲率,理论计算指出,在三维外尔半金属[11,47–51]、三维拓扑绝缘体[52]、二维过渡金属硫族化合物[10,53–55]、二维莫尔超晶格[22,25,27–29,31,32]以及某些低对称性晶体[56–62]中可以实现非线性霍尔效应.

2.2 无序导致的非线性霍尔效应

在贝里曲率偶极矩的理论被提出之后,人们开始思考是否还有其他因素可以导致非线性霍尔效应.Du 等[16]、Isobe 等[17]和König 等[63]在半经典玻尔兹曼输运方程的框架下,发现无序所导致的边跳作用(side-jump)和斜散射(skew-scattering)同样会对非线性霍尔效应产生影响.此外,人们还试图突破半经典框架[64–69].Xiao 等[64]发现在量子动力学理论中,带间相干效应会对霍尔电导有额外贡献,这一贡献在半经典理论中不存在.Du 等[65]利用费曼图构建了非线性霍尔效应的量子理论,发现了更多半经典描述中不存在的量子修正项.

非线性霍尔效应总是要求费米面穿过能带,因此无序散射不可避免,无序对霍尔电导的贡献甚至会比贝里曲率偶极矩更大.无序和贝里曲率偶极矩的并存使非线性霍尔效应的研究变得更加有趣和复杂.接下来介绍区分这两个机制的3 种方式(见表1): 分析材料对称性,测量纵向的倍频信号,测量非线性霍尔信号对纵向电导的依赖关系.

表1 非线性霍尔效应两种机制的比较Table 1.Comparison between dipole-and disorder-induced nonlinear Hall effect.

第一,对称性分析可以帮助区分无序与贝里曲率偶极矩这两个机制.以二维体系(z方向不存在电极)为例,非零的贝里曲率偶极矩只在对称性极低的体系中存在,材料至多只能存在一条镜面对称轴(对应点群C1,C1v)[8].而无序导致的非线性霍尔效应在更高的对称性下依然可能存在.比如,在C3,C3h,C3v,D3h和D3这些点群中,贝里曲率偶极矩为零,但无序贡献不为零,可以观察到纯粹的无序导致的非线性霍尔效应[65].需要注意的是,表1中对非线性霍尔效应的对称性分析中仅考虑旋转轴垂直于二维平面(旋转轴为z轴)的情况,如果旋转轴在二维平面内,在C2和C2v点群中也可以产生二维体系的非线性霍尔效应.

第二,无序与贝里曲率偶极矩导致的效应具有不同的纵向响应.贝里曲率偶极矩引起的非线性信号可以由公式描述.这一公式说明贝里曲率偶极矩引起的信号垂直于纵向输入电压Eω,只有霍尔方向(横向)的分量.而无序导致的非线性信号则没有方向性,纵向与横向应该有同量级的信号输出.

第三,无序与贝里曲率偶极矩导致的非线性霍尔信号对于纵向电导的依赖性不同.根据计算,非线性霍尔效应的霍尔电压与纵向电导σxx存在标度关系,

2.3 非线性霍尔效应的实现

图1 总结了目前为止各种实现非线性霍尔效应的非莫尔超晶格体系.根据最早Fu 提出的理论,实现非零贝里曲率偶极矩最简单的模型是倾斜的狄拉克锥.因此,非线性霍尔效应最有可能在外尔半金属,拓扑绝缘体或过渡金属硫族化合物此类具有非零贝里曲率以及倾斜能带的材料中实现.事实上,非线性霍尔效应确实首先在外尔半金属中实现.双层WTe2具有一对非对称耦合的狄拉克费米子,因此具有非零的贝里曲率偶极矩.2019年,Ma等[12]在无外磁场的情况下,对双层WTe2施加交流电流,观测到了与注入电流成平方关系的二倍频霍尔电压.此外,由于观测到的非线性霍尔效应来源于贝里曲率偶极矩,霍尔方向的电压响应远大于纵向电压响应,非线性霍尔角接近90°.几乎同一时间,Kang 等[13]报道了多层WTe2中的非线性霍尔效应,通过测量霍尔电导率的温度依赖性,发现内在的贝里曲率偶极矩和外在的无序散射都对观察到的非线性信号做出了贡献.Xiao 等[86]报道了WTe2中层相关的贝里曲率偶极矩导致的非线性霍尔效应,发现极性反转相变可以有效地调控材料贝里曲率偶极矩,在奇数层WTe2中甚至可以造成贝里曲率偶极矩反号的现象.Tiwari 等[71]、Ma 等[87]和Shvetsov 等[88]研究了更厚WTe2以及具有类似晶体结构的MoTe2中的非线性霍尔霍尔效应,发现材料越厚,无序散射在产生非线性信号时占比越高,甚至能占据主导地位.

图1 实现非线性霍尔效应的各种非莫尔超晶格材料,图片来源文献[19,71—85]Fig.1.Experimental observation of the nonlinear Hall effect in various kinds of non-moiré materials.Figures are reproduced from Refs.[19,71–85].

由于散射导致的非线性霍尔信号大小由杂质浓度决定,而杂质浓度在实际应用中较难调控,人们将非线性霍尔效应的实验研究扩展到了其他材料,试图寻找其他贝里曲率偶极矩占据主导地位的材料.在外尔半金属Ce3Bi4Pd3,TaIrTe4,NbP,(Pb1–xSnx)1–yInyTe 中[72,89–91],人们观测到了贝里曲率偶极矩导致的非线性霍尔效应.其中,TaIrTe4[72]和NbP[19,89]中贝里曲率偶极矩引起的非线性霍尔效应甚至可以在室温下存在,展示了非线性霍尔效应在倍频和整流相关应用方向上巨大的潜力.此外,在拓扑绝缘体Pb1–xSnxTe[74],ZrTe5[75],自旋-能谷锁定的狄拉克材料BaMnSb2[76],狄拉克半金属Cd3As2[88],有机材料α-(BEDT-TTF)2I3[92]等具有非零贝里曲率偶极矩的材料中,人们也观测到了非线性霍尔信号.

上述介绍的都是自身具有贝里曲率偶极矩的材料.由于非零贝里曲率偶极矩对材料对称性的要求,在实现非线性霍尔效应时可选择的材料十分有限.部分材料需要复杂的合成方法,甚至不能在空气中稳定存在,严重限制了非线性霍尔效应的实际应用.此外,这些材料的电子性质由晶体结构和成分组成决定,难以按照要求修改.这降低了我们优化非线性霍尔效应信号大小的能力.因此,研究者们开始思考在自身没有贝里曲率偶极矩的材料中是否也能产生非线性霍尔效应.在拓扑绝缘体Bi2Se3和外尔半金属CoTe2中,He 等[79]和Hu 等[80]分别发现了纯粹的无序导致的非线性霍尔效应.通过堆叠不同材料,Duan 等[81]在WSe2/SiP 界面上、Lesne 等[93]在LaAlO3/SrTiO3界面上观察到了非零贝里曲率偶极矩.在具有镜面与滑移镜像对称性的WTe2块材内,Ye 等[82]发现,通过施加面内直流电场打破对称性,可以实现贝里曲率偶极矩由无到有的变化.除此以外,应力也可以打破对称性,产生非零贝里曲率偶极矩.在2H相过渡金属硫族化合物中,Son 等[83]将MoS2放在柔性衬底上,Qin 等[84]将WSe2放在压电衬底上,均观察到了应力导致的非零贝里曲率偶极矩.Ho 等[85]将双层石墨烯放在人工制备的波纹状BN 上,同样测量到非线性霍尔效应.不足的是,由于材料的贝里曲率和能够承受的应力有限,目前通过施加应力产生的贝里曲率偶极矩往往较小(埃米量级).是否还有其他的方法或是材料能够产生更大、更方便调控的非线性霍尔信号呢?

3 二维莫尔超晶格的特性

随着二维范德瓦耳斯堆叠技术的发展,人们意识到,当以较小的旋转角度堆叠具有相同或相似晶格常数的两片二维层状材料时,会产生如图2 中间所示的二维莫尔超晶格.二维莫尔超晶格在小转角时自发的原子重构现象会形成应力场打破材料的对称性(图2(a),(b)[94]),并且有机会有较大的贝里曲率(图2(c),(d)[30]).这两点特性使得贝里曲率偶极矩能够存在,因此能够产生非线性霍尔效应.此外,莫尔超晶格还具有相互作用强(图2(e),(f)[36]),能带及输运性质可调(图2(g)[39])这两点特性.在这一系统中,非线性霍尔信号可能会展现出普通材料没有的特殊性质,并能够便捷地被转角、载流子浓度、外加电场等参数调控,极大拓展了非线性霍尔效应的应用空间.以下对这4 种特性进行详细介绍.

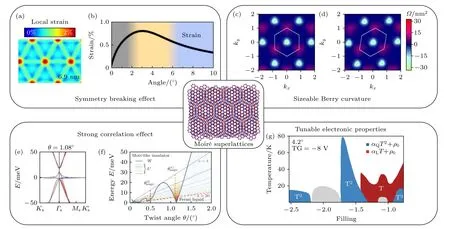
图2 二维莫尔超晶格的特性 (a)2.6°转角MoS2 的局部应变图[94];(b)系统中平均应力大小与旋转角度的关系[94];(c)无应力的情况下,转角WSe2 第一莫尔价带的贝里曲率分布,白色六边形对应莫尔布里渊区[30];(d)沿zigzag 方向引入0.6% 应力后的贝里曲率分布[30],不均匀的分布可以诱导贝里曲率偶极矩的产生;(e)1.08°转角双层石墨烯的能带结构,蓝线标注的两个能带十分平坦[36];(f)不同转角下能带带宽W(蓝色粗线)与库仑相互作用能U(细彩色线)比较[36];(g)转角过渡金属硫族化合物中可调控的电子特性,蓝色区域为费米液体(T2)态,红色区域为奇异金属(T-linear)态,灰色区域为绝缘态[39]Fig.2.Characteristics of two dimensional moiré superlattices: (a)Calculated patterns of local strain for twisted MoS2 at twist angle 2.6°[94];(b)the average (local)strain in the system as a function of twist angle[94];(c)the Berry curvature of the top moiré valence band of twisted WSe2 without strain.The white hexagon indicates the moiré Brillouin zone[30];(d)the Berry curvature distribution after introducing a strain strength of 0.6% along zigzag direction[30],the unbalanced distribution results in finite Berry curvature dipole;(e)the band energy E of magic angle twisted bilayer graphene calculated using an ab initio tight-binding method,the bands shown in blue are ultra-flat[36];(f)comparison between the bandwidth W (thick blue line)and the on-site Coulomb interaction energy U (thin coloured lines for different values of κ)for different twist angles θ[36];(g)a summary of tunable electronic properties in twisted transition metal dichalcogenides verified by different temperature dependences,blue showed Fermi liquid (T2)behaviour,red showed strange metal (T-linear)behaviour,grey showed insulating behaviour[39].

3.1 二维莫尔超晶格的对称性

考虑到非零贝里曲率偶极矩只在低对称性材料中存在,因此分析莫尔超晶格的对称性是很有必要的.以常见的转角石墨烯和转角过渡金属硫族化物为例: 转角石墨烯属于D6点群,转角2H相过渡金属硫族化合物较为复杂,同质结为D3点群,异质结为C3v点群.虽然莫尔超晶格的对称性相较转角之前有所降低,材料仍然具有三重或六重旋转对称性,这一对称性会使得材料贝里曲率偶极矩为零.只有1T相过渡金属硫族化合物这一类本身对称性就比较低的材料旋转堆叠后形成的莫尔超晶格才满足非线性霍尔效应的对称性要求.这是否意味着非线性霍尔效应只能在转角1T相过渡金属硫族化合物中存在呢? 答案是否定的.

以上的点群描述的都是完美的莫尔超晶格材料.而在实际中,范德瓦耳斯相互作用能和界面弹性能会导致原子发生重构现象并产生应力场.这一现象在石墨烯/BN 超晶格[95]、转角石墨烯[96]、转角过渡金属硫族化合物[97–100]中都已被观察到.在这些材料中,由于不同区域具有不同堆叠方式和不同的堆叠能量,在原子重构作用下,堆叠能量低(高)的区域会扩张(收缩).以转角MoS2为例,最终会形成如图2(a)所示的由畴壁分隔的具有三角形Bernal 堆积构型的畴阵列[94].通过观察透射电子显微镜中衍射图像的强度,Yoo 等[96]发现转角石墨烯中的原子重构现象仅在θ＜1°比较明显,随角度变大逐渐减弱.与转角石墨烯相比,转角过渡金属硫族化合物因过渡金属硫族化合物缺乏反转对称性而具有更多样的特性.研究者们通过透射电子显微镜、扫描隧道显微镜、原子力显微镜等多种手段对不同转角、不同堆叠层数的转角过渡金属硫族化合物进行观察,发现在θ<3°的样品中均可观察到原子重构现象[97–100].原子重构会在超晶格中产生复杂的应力场(图2(b))[94,101],此外,在样品制备过程中也会引入一些微小应力,这一应力足以打破材料对称性.Xie 等[102]和Kerelsky 等[103]在扫描隧道显微镜下观测到的低对称性图形证实了这一点.因此,小转角时,莫尔超晶格的对称性被自身的原子重构或外界应力打破,满足非线性霍尔效应的要求.

3.2 二维莫尔超晶格的贝里曲率特性

除了需要满足对称性要求外,产生贝里曲率偶极矩的另一个条件是材料有非零的贝里曲率.Serlin 等[104]和Sharpe 等[105]发现,在魔角石墨烯导带被填充至3/4 时,电子填充到自旋和能谷都极化的具有非零陈(Chern)数的莫尔子带,导致了可观测的反常霍尔效应.这一现象证明转角石墨烯体系具有非平庸的拓扑性质.Ma 等[106]和Sinha 等[107]分别在单层+单层和双层+双层的转角石墨烯中观测到了由非平庸拓扑和贝里曲率导致的非定域(nonlocal)输运信号.不仅如此,后续的理论计算和实验测量发现转角石墨烯中的贝里曲率可以影响体系的输运性质: 贝里曲率分布的均一性可以影响转角石墨烯中的分数关联绝缘态[108,109],超导刚度也与量子几何相关[110,111].虽然贝里曲率对转角石墨烯输运性质的具体影响还有待进一步研究,目前研究足以说明转角石墨烯体系中具有非零的贝里曲率.

单层六方结构过渡金属硫族化合物由于反演对称中心的缺失而具有非零的贝里曲率[112–117],对于转角过渡金属硫族化合物,不同研究组都对其贝里曲率进行过计算(图2(c),(d)[30]),并对贝里曲率对材料性质的影响进行过预测.Wu 等[118]计算了转角MoTe2中的贝里曲率,通过对莫尔布里渊区内的贝里曲率进行积分,发现莫尔超晶格的能带具有非平庸的拓扑性质.当费米面处于第一和第二莫尔价带之间的能隙时,系统是一个量子自旋霍尔绝缘体.Yu 等[119]对实空间中转角MoSe2贝里相位的分布进行了计算,同样认为系统可以实现量子自旋霍尔效应.Devakul 等[120]计算了转角WSe2的能带及贝里曲率,认为莫尔超晶格中的平带和均匀分布的贝里曲率相结合,有望在分数填充时实现分数量子反常霍尔效应.实验结果与理论预测一致,Li 等[121]制作了接近60°转角的MoTe2/WSe2,在体系价带半填满时观测到了量子反常霍尔效应,在价带完全填满时观测到了量子自旋霍尔效应.Cai等[122]和Zeng 等[123]在转角MoTe2体系中,通过光学手段测到了2/3 和3/5 分数填充处的分数量子反常霍尔效应.这一系列研究都说明转角过渡金属硫族化合物具有非零贝里曲率,可以作为研究非线性霍尔效应的平台.

3.3 强关联效应

电子在晶体内的运动会受到晶格周期势的影响,从而形成电子能带结构.莫尔超晶格会产生空间尺度几十甚至上百倍于原子晶格常数的周期性势场,反映在倒空间内,就是布里渊区缩小,能带发生折叠产生带宽为几或几十meV 的平带(图2(e)).在这样的平带中,电子与电子之间的库仑相互作用强度将超越由带宽决定的电子动能(图2(f)),引发强关联效应[36].

早在2011年,Bistritzer 和MacDonald[124]就计算了不同转角时转角石墨烯的能带结构.他们发现,当旋转角度小于2°时,两层石墨烯之间的层间耦合会变得很强,最低能带的带宽和狄拉克点的费米速度会发生急剧变化,并呈现出非单调行为.在某些独特的角度(θ=1.05°,0.5°,0.35°,0.24°,0.2°),即现在公认的魔角(magic angle)处,狄拉克点费米速度为零.同时,最低导带和最高价带极为平坦,可以导致强关联效应.然而由于技术发展的限制和样品制备的困难,较少有课题组实现精确的转角,对转角石墨烯的探索集中在范霍夫奇点以及莫尔能带全填满处的绝缘态[125–130].直到 2018年,Cao等[36]成功制备出魔角石墨烯电子器件.他们发现,魔角石墨烯在能带半填充时表现出绝缘态,并认为这种绝缘态可能来源于电子在超晶格中局域化而产生的莫特相变,这在没有强关联效应的情况下是不可能出现的.此外,通过调节载流子浓度使体系脱离这些关联绝缘态时,他们还观察到了与铜氧化物高温超导类似的超导现象.超导转变温度与玻色爱因斯坦凝聚温度的比值高达0.37,说明观测到的超导来源于电子-电子之间的强相互作用而不是电子-声子耦合[34].这两项发现证明转角体系是研究强相互作用的理想材料,在短时间内引起了科研人们的兴趣.

随后,人们在各种转角体系中观察到了更多强关联作用导致的有趣物理现象.在非魔角单层+单层转角石墨烯,双层+双层转角石墨烯,单层+双层转角石墨烯,单层+单层+单层转角三层石墨烯等各种石墨烯超晶格中,探测到了诸如整数和分数填充的关联绝缘态[131–140]、超导[141–144]、奇异金属态[145]、向列相[146–148]等现象.在转角过渡金属硫族化合物中,由于其能带带宽随角度连续变化,强关联效应可以在更大角度范围内出现.在转角WSe2,WSe2/WS2,MoSe2/WS2和MoSe2/WSe2体系中探测到了诸如关联绝缘态[37,149]、Wigner 晶格态[150]、非传统铁电[151]、莫尔激子[152–155]等物理现象.目前看来,强关联效应在小转角莫尔超晶格体系中普遍存在,这一效应是否会对非线性霍尔效应产生影响成为一个值得探索的问题.

3.4 可调控的电子特性

在莫尔超晶格体系中探索非线性霍尔效应的另一个好处是莫尔超晶格的能带和输运性质可以便捷地被组成成分、转角、载流子浓度、电场等各个因素调控.通过选择不同的二维材料和不同的堆叠方式,可以在保留单层二维材料特殊性质的同时按需设计体系对称性、自旋自由度和能谷自由度等参数,实现对体系结构和物性的控制.

通过控制两层材料之间的转角,可形成具有不同周期的莫尔超晶格.同质结的超晶格周期长度L与旋转角度θ 关系为L=a0/2sin (θ/2),其中a0为材料的晶格常数.异质结的超晶格周期长度为,其中δ=|a2-a1|/a2为两种材料晶格常数a1和a2的不匹配度.不同转角对应不同周期性势场以及不同能带宽度,1.5°以上的转角过渡金属硫族化合物的能带宽度甚至随转角单调变化[37,120],方便人们调控.

此外,通过改变载流子浓度和电场,可以连续调节能带结构,实现能隙的开启和闭合以及不同输运能态的切换.在以魔角石墨烯为代表的转角石墨烯体系中,通过调节载流子浓度,系统可以从普通绝缘态切换到奇异金属态、关联绝缘态甚至铁磁态[145,156].而在转角过渡金属硫族化合物中,Li 等[38]、Ghiotto 等[39]和Huang 等[30]观察到了载流子浓度和电场引发的金属-绝缘体连续相变,在相变点附近看到了关联绝缘态、费米液体和奇异金属态(图2(g)).这种丰富的电子态不仅可以使人们探索不同电子态以及量子临界位置的非线性霍尔效应,对非线性霍尔效应的基本机制有新的认识,还极大拓展了二维材料的功能空间,对设计新型电子和光电器件非常重要.

4 石墨烯超晶格中非线性霍尔效应的进展

对石墨烯超晶格中非线性霍尔效应的探索起源于理论预测的巨大贝里曲率偶极矩.Pantaleón等[29]用一个单轴应力描述原子重构产生的应力场,对有应力的转角石墨烯中的贝里曲率偶极矩做出计算.他们发现,应力可通过在两层中产生相反符号的有效规范场(gauge field)以及改变堆叠结构从而改变层间隧穿效应,这两种效应显著扭曲能带结构(图3(a)).转角石墨烯中平带的出现使得费米速度和贝里曲率集中分布在能带反交叉(anticrossing)的位置附近(图3(b)),而不是像普通材料一样弥散在整个布里渊区中,因而体系的贝里曲率偶极矩能达到十几纳米(图3(c),(d)),比普通材料大两个数量级.Zhang 等[22]计算了不同转角及不同应力大小的转角石墨烯中的贝里曲率偶极矩.他们发现,巨大的贝里曲率偶极矩仅在转角为魔角1.1°附近时出现(图3(e)),这是由于其他转角时体系的能带宽度远大于应力导致的规范势,应力并不能显著影响贝里曲率的均匀分布.此外,他们还计算了应力-栅压空间内的偶极矩,发现应力为±0.2% 时的导带顶端和价带底端出现了拓扑能带反转导致的蝴蝶状图案(图3(f)).这一特性可以用于拓扑相变的探测.

图3 石墨烯超晶格中非线性霍尔效应的理论研究 (a)1.05°魔角石墨烯在0.3% 应力下的能带结构(红线和黑线),无应力时的能带结构为绿色虚线[29];(b)第一莫尔导带的贝里曲率分布[29];(c),(d)贝里曲率偶极矩x (c)和y (d)方向的分量在莫尔布里渊区内的分布,插图为贝里曲率和偶极矩集中区域的放大图[29];(e)贝里曲率偶极矩对旋转角度和掺杂的依赖性,转角接近第一个魔角时,带边出现约200 Å的巨大贝里曲率偶极矩[22];(f)贝里曲率偶极矩对于费米面和应力的依赖性[22];(g)拓扑相变过程中能带边缘附近贝里曲率分布的变化,贝里曲率偶极矩在相变过程中发生符号反转[27]Fig.3.Theoretical studies of the nonlinear Hall effect in graphene superlattices: (a)Band structure of twisted bilayer graphene with a twist angle θ=1.05° and uniaxial strain of 0.3% (red and black lines),the band structure for the unstrained twisted bilayer graphene is shown as green dotted lines[29];(b)Berry curvature of the bottom moiré conduction band[29];(c),(d)distribution of the x (c)and y (d)component of the Berry curvature dipole,insets in each panel are the enlarged regions where the corresponding Berry curvature and dipole are concentrated[29];(e)twist angle and doping dependence of the Berry curvature dipole,a giant Berry curvature dipole of order～200 Å appears near all the band edges for a twist angle near the first magic angle[22];(f)evolution of the Berry curvature dipole with respect to both the Fermi energy EF and the strain ε[22];(g)the change of the Berry curvature distribution near the band edges during the topological phase transition,Berry curvature dipole undergoes a sign reversal across the phase transition[27].

在理论方面将非线性霍尔效应与探测体系相变关联起来的还有Chakraborty 等[27]、Pantaleón等[25]和Yang 等[28].Chakraborty 等[27]计算了有应力的双层+双层转角石墨烯中的非线性霍尔响应,发现垂直电场引起的拓扑相变伴随着特定动量点的能带闭合,会改变该动量点附近的贝里曲率的分布,从而导致相变时贝里曲率偶极矩的符号变化以及非线性霍尔响应的方向变化(图3(g)).Pantaleón 等[25]发现当魔角石墨烯能带被填充到某些位置时,远程(remote)能带对霍尔信号贡献很大,而中心能带的贡献会受到抑制.在出现掺杂引起的能带反转时,远程能带引起的霍尔信号会得到显著增强.Yang 等[28]认为非线性霍尔响应可以用于区分能带半填满时金属-绝缘态相变后绝缘态的性质.体系是自旋极化的谷间相干态时,C2T对称性的存在将导致贝里曲率偶极矩为零,无法观察到非线性霍尔效应.仅当体系是自旋极化的量子霍尔态时,贝里曲率偶极矩才不为零.自旋-能谷极化态和自旋极化的能谷霍尔态可以靠磁场下的非线性霍尔效应区分.对于自旋极化的能谷霍尔态,仅当z方向存在磁场时,贝里曲率偶极矩才非零.而对于自旋-能谷极化态,在x方向或z方向存在磁场时,都能出现非零贝里曲率.

实验上,Sinha 等[20]在双层+双层转角石墨烯材料中测到了贝里曲率偶极矩导致的非线性霍尔效应.在这一体系中,垂直电场可以通过调制能带结构来改变平带的陈数,引发拓扑相变.他们发现,相变前后体系中的非线性霍尔信号发生剧烈变化(图4(a)),从实验数据中得出的贝里曲率偶极矩出现变号现象(图4(b)).他们对体系的能带计算进一步说明贝里曲率偶极矩的变号的确来源于垂直电场引发的拓扑相变.这项工作不仅证明了石墨烯超晶格中贝里曲率偶极矩的存在,还展示了非线性霍尔效应在探测拓扑相变方面的可能性.

图4 石墨烯超晶格中非线性霍尔效应的实验研究 (a)非线性霍尔电压(左轴)和纵向电导率的平方(右轴)对转角双层+双层石墨烯中垂直电场的依赖性,能带的谷陈数在两个区域中发生变化(区域 I 具有浅绿色背景,区域 II 具有浅蓝色背景)[20];(b)贝里曲率偶极矩在两各区域内符号相反[20];(c)石墨烯/氮化硼超晶格中的非线性电导率与迁移率的立方成线性关系,表明观测到的非线性霍尔效应由无序引起[24];(d)杂质、声子和混合偏斜散射对非线性霍尔信号的贡献对温度依赖性[23];(e)非线性霍尔效应的相图,虚线表示贝里曲率偶极矩和散射对非线性霍尔信号的贡献相等的位置,红色(蓝色)区域代表偶极矩(散射)主导的区域[26];(f)转角单层+单层石墨烯中的二次谐波霍尔电压符号随掺杂和垂直电场改变[26]Fig.4.Experimental observations of the nonlinear Hall effect in graphene superlattices: (a)Dependence of normalized nonlinear Hall voltage (left axis)and square of longitudinal conductivity (right axis)on displacement field in twisted double bilayer graphene,the valley Chern numbers of the bands change across the two regimes (regime I with the light-green background and regime II with the light-blue background)[20];(b)extracted Berry curvature dipole shows opposite sign for the two regimes[20];(c)the nonlinear conductivity scales linearly with the cube of mobility in graphene/BN superlattices,indicating disorder-induced nonlinear Hall effect[24];(d)temperature dependence of the distribution of the contributions to the nonlinear Hall signal from impurity,mixed,and phonon skew scatterings[23];(e)phase diagram of the nonlinear Hall effect,the dashed line represents the position where the Berry curvature dipole and the scattering contribute equally to the nonlinear Hall signal,the red (blue)area represents the dipole (scattering)dominated area[26];(f)the second harmonic Hall voltage in twisted bilayer graphene change signs when tuning the filling and displacement field[26].

有趣的是,在单层石墨烯与BN 形成的超晶格[24]以及单层+单层转角石墨烯[23]中,实验显示观测到的非线性信号由无序导致.He 等[24]认为,单层石墨烯与BN 形成的超晶格体系中存在的三重旋转对称性会导致贝里曲率偶极矩为零,而体系的空间反演对称性破缺会使得石墨烯K和K′ 能谷具有相反的手性,导致斜散射的发生,从而产生非线性信号.实验中,他们在零磁场下在纵向(xx)和横向(xy)方向上同时观察到显著的正比于输入电流二次方的二倍频信号.不同温度下的非线性霍尔信号显示二倍频电导与系统迁移率的三次方成正比(图4(c)),换算后即为以上两个证据证明观察到的非线性霍尔信号由斜散射造成.

在转角石墨烯体系中,Duan 等[23]观察到了无序导致的非线性信号并对其进行仔细研究.他们发现,零温下的非线性信号完全由杂质斜散射决定.随着温度升高,声子斜散射贡献增加,但杂质斜散射贡献减少,在较高温度下两种机制会互相竞争(图4(d)).虽然这两项工作默认三重旋转对称性没有被打破,各种实验表明器件制备过程中引入的应变而引起的三重旋转对称性破缺会导致非零的贝里曲率偶极矩.尽管Duan 等[23]认为,即便应力存在,应力产生的贝里曲率偶极矩产生的非线性信号应该比观察到的无序导致的非线性信号小3 个数量级,Pantaleón 等[25]认为Hartree 势和BN 衬底的存在而导致的能带结构重整化可以增大贝里曲率偶极矩,在无需考虑无序的情况下解释Duan 等[23]观察到的大信号.石墨烯超晶格体系中的非线性霍尔效应究竟是由贝里曲率偶极矩主导还是由无序主导,成为了一个需要解决的问题.

Zhong 等[21]通过调节AB-BA 堆叠双层+双层转角石墨烯中的载流子浓度和垂直电场,发现了由无序主导向贝里曲率偶极矩主导的非线性霍尔效应的转变.具体来说,当系统电导较大时,贝里曲率偶极矩占主导;当系统电导变小时,斜散射逐渐加强并超越偶极矩的贡献.

而在最新一项工作中,Huang 等[26]在高迁移率单层+单层转角石墨烯样品中探测到了非线性霍尔信号.消失的纵向非线性信号以及非线性霍尔信号对载流子浓度、垂直电场、温度的响应证明信号来自贝里曲率偶极矩而不是无序.他们对石墨烯超晶格中两种产生非线性霍尔效应的机制的研究进一步表明: 贝里曲率偶极矩在应力大且杂质浓度低的样品中占主导;反之,无序在应力小且杂质浓度高的样品中主导(图4(e)).此外,虽然过往的实验结论认为垂直方向的电场对这个体系非线性霍尔效应的调制能力是有限的,并不会导致莫尔能带产生或关闭能隙[124,130].Huang 等[26]发现垂直方向电场能够在不改变能带拓扑性质的同时(没有发生拓扑相变),通过改变贝里曲率热点在能带上的位置有效地调控贝里曲率偶极矩,甚至改变偶极矩的方向(图4(f)).这项工作不仅使得人们可以利用非线性霍尔效应来探测能带内贝里曲率在动量空间的分布,而且对于实现更稳定的拓扑输运,关联绝缘态和超流体具有重要的意义.

5 过渡金属硫族化合物超晶格中非线性霍尔效应的进展

作为目前除石墨烯超晶格体系外另一类具有稳定强关联效应和非平庸拓扑性质的体系,过渡金属硫族化合物超晶格中的非线性霍尔效应也引起人们的关注.Huang 等[30]首先在单层+单层转角二硒化钨体系中观察到贝里曲率偶极矩导致的非线性霍尔效应.他们发现,在转角WSe2的第一个莫尔价带被半填满时,系统的非线性霍尔电压信号相比于远离半填满状态时出现了2—3 个数量级的增强(图5(a)).相应的非线性霍尔信号产生效率为1000 V–1,比之前报道的非转角材料的最大值(6.25 V–1)至少高两个数量级.尽管远离半填充的非线性霍尔信号可以用非零应力导致的非零贝里曲率偶极矩来解释,半填充附近非线性霍尔信号的巨大增强无法用有限的贝里曲率来理解(图5(b)).为此,他们研究了体系半填充附近体系电阻随温度的变化,在半填充附近观测到连续莫特转变以及与重费米子材料类似的质量发散特性,发现这一特性可以用于解释观测到的巨大非线性信号(图5(c)).这项研究不仅展示了电子-电子相互作用如何与贝里曲率偶极矩结合产生新的量子现象,而且首次展现了非线性霍尔效应作为一种新工具研究量子临界(凝聚态物理学中最具挑战性和有趣的问题之一)的潜力.

图5 过渡金属硫族化合物超晶格中非线性霍尔效应的研究 (a)转角WSe2 中在半填充附近观察到巨大的非线性霍尔信号[30];(b)非相互作用框架中理论计算的偶极矩(下图)可用于理解远离半填充位置(上图)的实验数据[30];(c)半填充时观察到的巨大信号(黑点)可用有效质量发散模型(红线)解释[30];(d)Dx (x 分量贝里曲率偶极矩)对Vz (垂直电场)和nh (空穴填充数)依赖性,Dx 在相变点附近显著增大[31];(e)转角双层WTe2 的能带结构(θ=29.4°)[32];(f)转角双层WTe2 (θ=29.4°)和普通双层WTe2 的贝里曲率偶极矩随温度的变化[32];(g)非线性霍尔信号在莫尔势存在(P <0)和不存在时(P >0)随填充因子的变化.仅当 P ＜ 0 时,才能在关联绝缘状态下观察到非线性霍尔信号[33]Fig.5.Studies of the nonlinear Hall effect in transition metal dichalcogenides superlattices: (a)Second harmonic Hall voltage versus filling in twisted WSe2,a sharp peak is observed near the half-filling[30];(b)theoretical calculated dipole in non-interacting picture(bottom panel)can be used to understand the experimental data away from half-filling (top panel)[30];(c)theoretical fitting using the effective mass divergence formula (red line)can be used to understand the observed giant signal at half filling (black dots)[30];(d)Vz (out of plane displacement field)and nh (number of holes per unit cell)dependence of Dx (x component Berry dipole),Dx is strongly enhanced near the phase transition point[31];(e)the band structure of twisted bilayer WTe2 (θ=29.4°)[32];(f)the temperature dependence of Berry curvature dipole for twisted bilayer WTe2 (θ=29.4°)and prefect bilayer WTe2[32];(g)filling-factor-dependent nonlinear Hall signal for with (P <0)and without (P >0)moiré potential,respectively.Nonlinear anomalous Hall resets are observed at the correlated insulating states only for P <0[33].

Hu 等[31]对这一体系的理论计算进一步显示,垂直电场的改变可以导致第一莫尔价带和第二莫尔价带相互接触并交换贝里曲率从而产生拓扑相变,相变点附近贝里曲率偶极矩会显著增强.更重要的是,他们发现非线性霍尔信号会在拓扑相变前后改变符号(图5(d)),这一发现提供了一种探测拓扑相变和平带拓扑特性的新方法.

相比于石墨烯超晶格,过渡金属硫族化合物超晶格的复杂性在于过渡金属硫族化合物本身可以具有六方晶系以外的晶体结构.比如,属于正交晶系的Td相WTe2比六方晶系的2H相WTe2能量更低.He 和Weng[32]提出,转角WTe2体系的能带结构十分复杂,当费米能级从电荷中性点偏移时,费米能级在狭窄的能量区域内经历多个能带反交叉(图5(e)),导致电荷中性点周围的贝里曲率偶极矩发生剧烈的符号变化.多次的能带交叉会使得能带边缘具有较大的贝里曲率梯度,从而导致巨大的贝里曲率偶极矩和强烈的非线性霍尔响应.以29.4°转角WTe2为例,He 和Weng[32]的计算表明体系的贝里曲率偶极矩在低温下(＜20 K)有显著提升,甚至能达到140 nm (图5(f)).

尽管转角WTe2体系中的非线性霍尔效应还没有在实验上被观测到,Kang 等[33]制备了双层Td-WTe2与单层1H-WSe2的莫尔超晶格,探测了这一面心长方点阵中的非线性霍尔效应.他们发现,由于双层Td-WTe2具有铁电特性,这一体系中的莫尔势场可以通过调节电场方向开启或关闭.在莫尔势场关闭的情况下,贝里曲率及其偶极矩集中在WTe2导带和价带边缘附近,非线性霍尔信号在电荷中性点附近很强;在莫尔势场开启并产生平带时,贝里曲率布里渊区内重新分布,相反符号的贝里曲率偶极矩集中在Hubbard 带边,从而导致在关联绝缘态处观察到非线性霍尔电压的剧烈变化(图5(g)).这一工作说明材料铁电特性对非线性霍尔效应的调控不仅可以发生在非莫尔超晶格材料中[86],对莫尔超晶格材料同样适用,展示了通过结合不同对称性材料来创造新的功能性莫尔超晶格的潜力.

6 总结与展望

由于非线性霍尔效应在整流以及倍频器件中巨大的应用潜力,该效应自提出以来一直受到人们的广泛关注.二维莫尔超晶格由于具有可观的贝里曲率、对称性破缺、强关联效应和可调控的能带结构这四点特性,可以为非线性霍尔效应的研究引入更多可能性.本文总结了以石墨烯超晶格和过渡金属硫族化合物超晶格为代表的二维莫尔超晶格中近年有关非线性霍尔效应的研究进展(不同系统中非线性霍尔效应的强度和主导机制已在表2 中列出),发现这两个系统各具特点,从基础研究的角度展现出了对非线性霍尔效应大小和方向的调控,以及利用非线性霍尔效应探测拓扑相变、贝里曲率动量空间分布和量子临界的潜力.根据本文内容,对二维莫尔超晶格中非线性霍尔效应的研究方向和潜在应用做出以下展望.

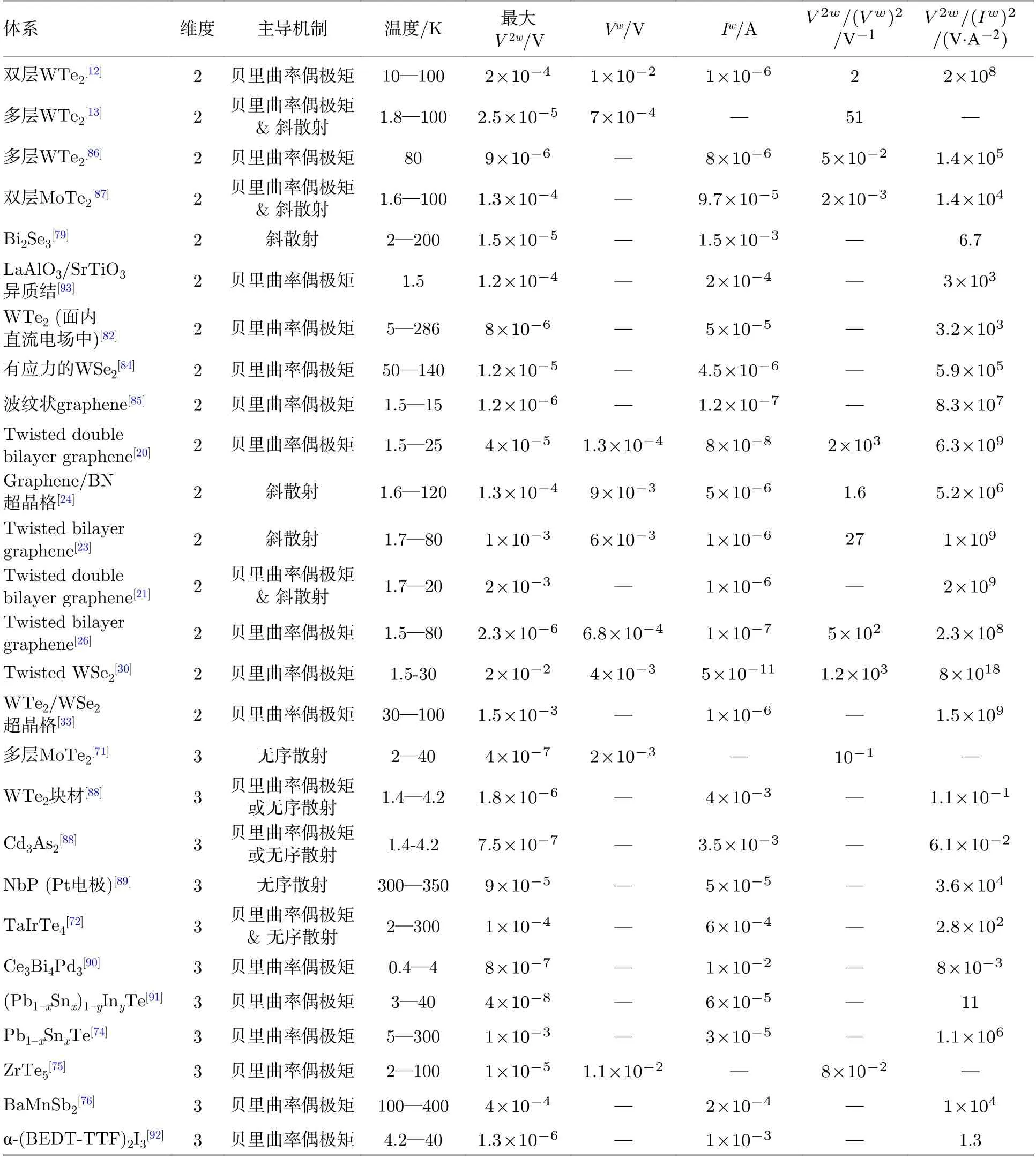
表2 不同材料系统中非线性霍尔效应实验总结.最大V 2w 为实验中测得的最大二倍频输出,V w,I w 为此时输入电压、电流,非线性霍尔效应强度可由 V 2w/(V w)2 或 V 2w/(Iw)2 反映Table 2.Nonlinear Hall effect observed in different systems.V 2w is the observed highest second harmonic signal,V w and I w are the input voltage and current at this time,respectively.The strength of the nonlinear Hall effect can be determined by V 2w/(V w)2 or V 2w/(Iw)2 .

6.1 寻找具有更大贝里曲率偶极矩的材料

目前实验观测到非线性霍尔效应的二维超晶格体系还局限于石墨烯和二硒化钨的超晶格系统.石墨烯和二硒化钨的能带本身都不具备倾斜的狄拉克锥结构,实现非零贝里曲率偶极矩是通过制备器件过程中引入的微小应力.作为基础研究的平台,微小的应力已经足以打破体系的三次对称性,产生可观测的非线性霍尔效应.而从未来应用的角度,器件还需要引入更大的应力以实现更大的贝里曲率偶极矩.一种可行的方法是利用化学气相沉积制备具有大应力结构的莫尔超晶格阵列(图6(a))[157].另一种有效的方法是采用第二类外尔半金属或者第二类狄拉克半金属这两类本身具有贝里曲率偶极矩的材料.比如,理论计算单层+单层转角WTe2的贝里曲率偶极矩可达到140 nm,远大于双层WTe2中的6 nm[32].更多转角第二类半金属材料的莫尔超晶格结构是否在费米面附近具有可观的贝里曲率偶极矩,还需要未来更多理论计算的研究[160].

图6 非线性霍尔效应的潜在研究和应用 (a)利用化学气相沉积制备具有大应力结构的莫尔超晶格阵列[157];(b)利用非线性霍尔效应探测莫尔超晶格的相变[158];(c)利用二维超晶格器件进行高灵敏度应力探测[159];(d)基于二维莫尔超晶格中非线性霍尔效应的太赫兹探测[19]Fig.6.Potential research area and application of the nonlinear Hall effect: (a)Fabrication of moiré superlattice arrays with large stress structures by chemical vapor deposition[157];(b)probing the phase transiton of moiré superlattice using nonlinear Hall effect[158];(c)high-sensitivity strain detection using two-dimensional superlattice devices[159];(d)terahertz detection based on nonlinear Hall effect in moiré superlattice[19].

6.2 研究产生非线性霍尔效应的其他可能机制

目前为止,大部分研究者认为贝里曲率偶极矩和无序是两种可以产生非线性霍尔效应的机制.但在实验中出现了观测到的二倍频霍尔信号远大于理论计算的情况[20],尽管作者用实验中应力的复杂性解释这一现象,我们不排除还有其他产生非线性霍尔效应机制的可能性.比如,目前大部分人在计算时仅考虑能带内的跃迁(intraband transition)对非线性霍尔效应的贡献,而Kaplan 等[161]的计算表明在多个能带同时存在的情况下,带间跃迁(interband process)可能会贡献额外的非线性霍尔效应信号.是否还有其他被忽略的贡献,以及是否还有独立于贝里曲率偶极矩和无序的新机制,是未来值得探索的问题.

6.3 利用非线性霍尔效应探测莫尔超晶格的相变

金属(掺杂)狄拉克系统中相互作用驱动的对称性破缺可以表现为埋在费米能级以下节点(nodal point)处的自发能隙生成.在这个转变过程中,线性电导率大小及变化是有限的,这使得在线性传输中直接观测变得相对困难.2020年,Rostami 和Juričić[158]提出了利用非线性霍尔效应作为反演对称性破缺时这种转变的直接探测方法(图6(b)),因为非线性霍尔电导率只有在反演对称打破时才是非零的.目前的实验也表明在体系相变点附近,非线性霍尔信号会发生剧烈的变化[20,30,86].我们相信,非线性霍尔效应可以作为新的探测手段,在探测体系相变方面发挥重要作用.

6.4 利用非线性霍尔效应研究二维莫尔磁性材料的磁结构

磁性材料中尼尔矢量(Néel vector)作为新型自旋电子器件的状态变量,其精确测量是一个具有挑战性的问题.理论研究发现非线性霍尔效应对尼尔矢量方向有灵敏的响应,可以用来探测PT 不变(PT-invatiant)反铁磁材料的磁序[162–165].利用二维超晶格结构调控范德瓦耳斯磁性材料的磁性行为是目前新兴的研究方向[166].我们相信未来非线性霍尔效应作为一个有效的探测手段,会在二维莫尔磁性材料的磁结构探测方面发挥出更大的作用.

6.5 基于二维莫尔超晶格的太赫兹探测和应力探测

高频整流广泛应用于红外、远红外和亚毫米波段的探测器和传感器技术.然而,电子二极管和光子二极管的工作频率之间存在所谓的太赫兹间隙(terahertz gap,0.1—10 THz)[167].该频率范围内的整流技术仍在开发中.通过在二维超晶格材料中调控贝里曲率偶极矩,有望实现室温下具有巨大响应和超高灵敏度的太赫兹探测(图6(d))[17].除此之外,二维超晶格材料器件在高灵敏度应力探测领域也有令人期待的潜力(图6(c))[159,168].