基于ASCAT风场数据的热带气旋风圈半径的研究

董海啸，冯佳俊，张渊智

（南京信息工程大学海洋科学学院，江苏南京 210044）

0 引言

环太平洋、大西洋大陆国家由于其独特和复杂的地理环境，自然灾害频发，其中热带气旋（Tropical Cyclone，TC）灾害[1]以其发生频次高、危害程度重、影响范围广和灾害链长而备受关注。TC是一种天气气候系统，体现了大气、海洋、陆地之间的相互作用，对TC 特征结构（强度和尺度）的研究对于TC的监测和预报都有重要的指导意义。

随着卫星遥感技术的发展，其具备的高时空分辨率和大面积同步观测的优越性极大地降低人力、物力观测成本，在过去的几十年已被广泛应用于无法获得现场数据的极端条件下TC 海表风场的研究。欧洲Metop气象业务极轨卫星携带的先进散射计ASCAT（Advanced Scatterometer）能够提供覆盖95%以上热带海洋的每日风场资料，尤其是在2009年11 月快速散射计QuikSCAT（Quick Scatteromete）失效以后，ASCAT成为TC预报和快速风矢量搜索算法[2]的重要数据来源，并已广泛应用于气象服务[3]。

ASCAT 风场数据已被广泛应用于海洋等领域的研究。高留喜等[4]利用QuikSCAT 和ASCAT 反演风场与浮标资料在中国南海北部进行统计检验分析，发现两套卫星资料在该区域有较好的适用性。RICCIARDULLI 等[5]对来自气象卫星Metop-A、Metop-B 和Metop-C 的ASCAT 风数据进行相互校准以获得稳定的气候数据记录。POLVERARI等[6]使用了2009—2017 年经过再处理的12.5 km 分辨率的ASCAT-A风数据进行分析，发现ASCAT对15 m/s以上风速存在低估情况，因此提出了一种基于12 m/s以上风速的校准方法。

与此同时，基于ASCAT 风场数据的TC 研究也有一定的进展。WIMMERS 等[7]基于ASCAT 散射计在内的多源卫星遥感数据改进了TC 中心定位算法（ARCHER-2），对比美国国家飓风中心最佳轨迹结果，中心修正误差的中值范围为24～49 km。LIU等[8]使用海洋二星B 卫星（HY-2B）散射计数据HSCAT 和ASCAT 提出了一种直接采用最大散射计风速来评估TC 强度的替代方法，评估了风半径r17（风速达到17 m/s）在确定TC 强度上的可行性。NI等[9]针对合成孔径雷达（Synthetic Aperture Radar，SAR）和ASCAT CMOD7 数据在TC 条件下进行风速优化，通过调整ASCAT 风速来匹配SAR 风速，可以使ASCAT 风速的误差减小约16.0 %。张圣雪等[10]结合风云二号F 星（FY-2F）、风云二号G 星（FY-2G）和ASCAT 数据基于偏角方差（Deviation Angle Variance，DAV）技术建立了TC 强度回归模型，对于验证集数据模型的均方误差为4.66 m/s，平均绝对误差为3.99 m/s，证实了该模型可以较好地估计TC强度。NI 等[11]提出了一种将计算最大1 min 持续风速作为Rankine 涡旋模型衰减参数函数的方法，以获得更准确的TC 强度估计，将此方法应用于2016—2017 年的ASCAT 风场数据后，结果优于MAYERS-RUF方法[12]。

上述研究大多以ASCAT风场作为数据源，围绕TC中心位置、强度、TC情况下风速产品优化校准等方面开展。不同强度的风圈具有不同的预报指示意义，34节（风速达到17.5 m/s）风圈半径（R34）可以表示TC 主体环流所带来的大风影响范围，一般以其大小来衡量TC 尺度。SOISUVARN 等[13]基于ASCAT 风场气候数据研究了2007—2012 年西北太平洋（Northwest Pacific，NWP）TC 的R34 和R50（50节的风圈半径），并提出了一种新的风圈半径表征技术，本文将在此基础上对ASCAT 数据在计算TC风圈半径方面进行进一步评估，尝试基于ASCAT风场数据计算2013—2022 年5—11 月发生在西北太平洋和北大西洋（North Atlantic，NA）TC 的R34和R50以扩充研究时间序列，采用Pearson相关分析法确定R34定义TC大小的可行性并对所有TC大小进行分类，对10 年间TC 风圈半径的变化进行统计分析。

本文将在第1 节中对所使用的数据进行介绍；在第2 节中对最佳路径数据和ASCAT 数据进行时空窗匹配提取TC 风场信息，通过TC 案例来展示本文所采用的基于ASCAT 风场数据R34 和R50 的计算方法；在第3 节中利用最佳路径数据对结果进行比较，用ASCAT 数据对TC 大小进行定义，并对10年间北大西洋和西北太平洋所有TC 样本的R34 和R50进行统计分析；最后在第4节中进行总结。

1 数据

1.1 ASCAT风场数据

ASCAT 是欧洲空间局（European Space Agency，ESA）发射的Metop气象业务极轨卫星上携带的仪器之一，由欧洲气象卫星应用组织（EUMETSAT）使用。Metop-A 是Metop 系列3 颗卫星中的第一颗，于2006 年10 月19 日发射，Metop-B于2012 年9 月17 日发射，Metop-C 于2018 年11 月7日发射。ASCAT 向海面发射特性良好的微波能量脉冲，并接收和记录产生的回波以传输到地面站，然后导出有关风速和风向的数据，其具备更好的分辨率和超过其前身（ERA 地球资源卫星ERS-1 和ERS-2上的有源微波仪器）两倍的覆盖范围，可以在短短5 d内实现近乎全球的覆盖范围。

ASCAT L2B 海岸风场产品是由荷兰皇家气象研 究 协 会（Royal Netherlands Meteorological Institute，KNMI）在L1B 级产品的基础上再加工而成，空间分辨率为12.5 km，采用改进的地球物理模型函数CMOD7 GMFs 将风矢量映射到后向散射信号值中，本文下载的数据分别来自Metop-A、Metop-C卫星，时间范围为2013—2022年的5—11月，空间范围为西北太平洋和北大西洋。

1.2 最佳路径数据

美国国家海洋和大气管理局（National Oceanic and Atmospheric Administration，NOAA）提供了最佳路径的TC 数据集，最佳路径数据来源于许多机构和数据集。在TC 形成期间，气象预报员对TC 的历史位置和强度进行观测，同时预测其未来的位置和强度。在风暴结束后（通常在当年台风/飓风季结束后），预报员收集所有可用的信息（来自陆地、浮标、船只等的相关报告、雷达数据、飞机数据和卫星数据等），利用这些信息对TC 的路径和强度做出最佳估计，因此形成“最佳路径”。随着时间的推移和技术的发展，相关机构对所有留存的数据进行再分析并更新较旧的最佳路径数据集。本论文选取美国源机构观测的时间范围为2013—2022 年的5—11月发生在NWP 和NA 编号入档的TC 最佳路径数据，包括每个观测时刻（世界时，下同）的风眼位置、中心最大风速、4 个象限的R34、R50 和TC 名称。计算数据集中的R34和R50时，对所有地理象限（NW、NE、SW、SE方向）的风圈半径进行方位平均。

2 研究方法

2.1 风速优化

ASCAT CMOD7 模型数据在TC 发生时会低估风速，CMOD7D[6]模型是CMOD7 模型的多项式变换。CMOD7D公式为：

式中：下标7D和7分别代指CMOD7D和CMOD7模型。使用该模型可对原始风场≥12 m/s 的风速进行优化，V7D和V7分别表示优化后和原始风场的风速。在相对平静的海域，即V7<12 m/s时可忽略V7D的值，即V7D值被V7取代。数据处理时需要将风矢量分解成水平分量（U）和垂直分量（V），计算公式为：

式中：风向变量direction 的单位是（°），风速speed 的单位是m/s。

2.2 时空窗匹配

由于最佳路径数据的时间间隔为3 h，通过时空窗匹配可过滤出ASCAT L2B 数据中的TC 风场。首先对最佳路径数据进行区域筛选，保留路径在NWP 和NA 海盆上的TC；然后进行时间窗匹配，利用最佳路径数据中每个TC的时间与ASCAT每日风场时间匹配（设置1.5 h阈值），同时以最佳路径数据中每个TC 路径中心位置为圆心，500 km 为搜索半径筛选出卫星数据中的TC风场。

在进行时空窗匹配时，为了提高R34 和R50 计算的准确性，对ASCAT风场数据按以下标准进行二次筛选：①TC 中心必须被刈幅覆盖，中间和边缘的距离必须大于1°；②TC 涡流结构必须有超过60%被刈幅覆盖；③目标区域内相邻网格点没有明显的风向冲突问题（风向模糊），存在明显TC 涡流的逆时针结构。

最终获得2013—2022 年的5—11 月NWP 和NA 海盆的ASCAT 风场共1 212 幅，对应形成于NA的TC 79个和NWP 的TC 132个，共211个TC 事件。匹配得到的TC 在其整个生命周期每个观测时刻的最大风速按照Saffir-Simpson 等级（即热带低压（Tropical Depression，TD）、热 带 风 暴（Tropical Storm，TS）、飓风等级1—5（Hurricane1—5，H1—5））进行分类，结果见图1。

图1 2013—2022年5—11月NWP和NA的TC最佳路径Fig.1 Best Track of TC during May and November in NWP and NA in 2013—2022

为了方便对每个TC 进行分类编号归档，我们按照在同一个TC 的生命周期内，ASCAT 散射计对其重复观测的次数进行进一步细化分类，结果见图2。经过时空窗匹配再筛选之后的TC 数据集中，ASCAT散射计对单个TC的重复观测次数大部分集中在1～6 次，共形成142 个TC，占总数的67.3%，每个重复观测次数与其对应的TC 个数相乘再累加后对应的数值1 212 则是进行时空窗匹配和二次筛选的ASCAT风场的幅数。

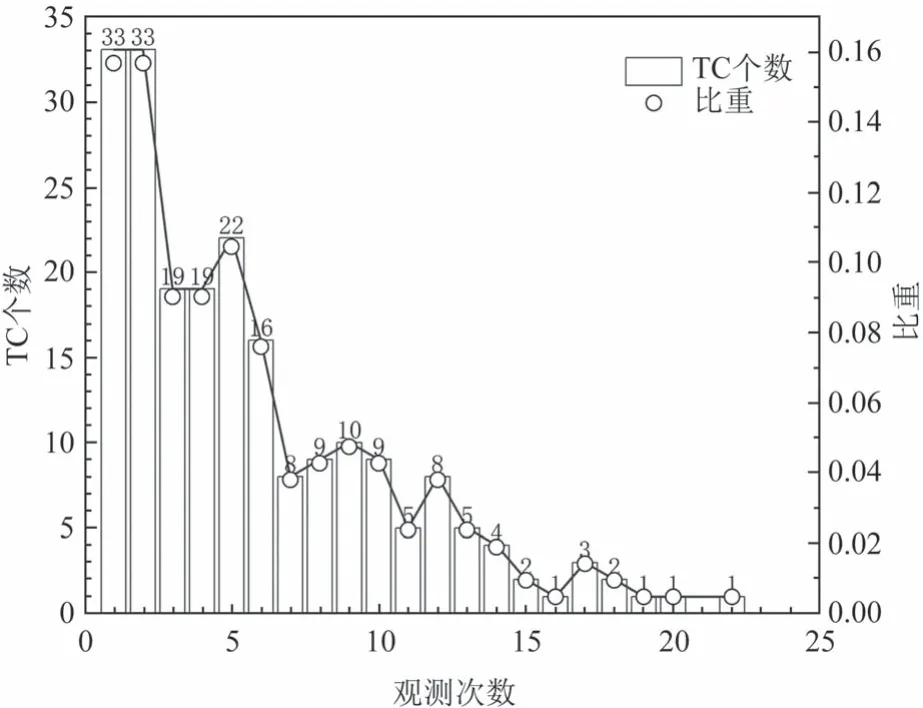
图2 TC-ASCAT观测次数分布Fig.2 Distribution of TC-ASCAT observations

进行案例研究的主要目的是验证R34 和R50 计算方法在卫星散射计观测资料中应用的适用性，因此案例选取遵循在同一个TC 的生命周期内散射计尽可能多地对其进行重复观测的原则，最终选取观测次数较多的1705号台风“奥鹿”（18幅）作为TC案例以便更好地进行本文风圈半径计算方法的结果展示。

ASCAT 分别于2017 年7 月25 日22 时12 分、28日11 时、31 日23 时30 分以及8 月3 日00 时27 分观测到了较为完整的台风“奥鹿”的海面风场，结果见图3。

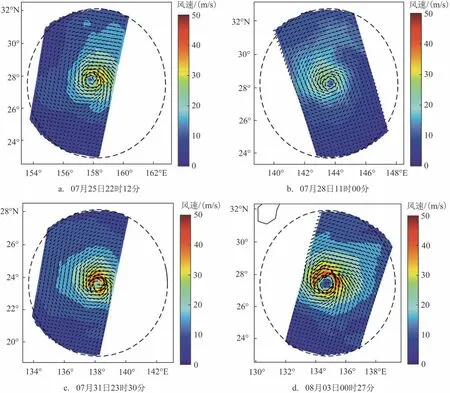
图3 ASCAT观测的台风“奥鹿”风场Fig.3 Wind field of Typhoon"Noru"observed by ASCAT

2.3 风圈半径

TC 大小是研究其结构的一个重要参数，通常被定义为最外层闭合等压线的平均半径（Radius of the Outermost Closed Isobar，ROCI）和海面风场风速为15 m/s 或17 m/s 时的平均半径[14]。但MERRILL[15]发现，ROCI 会随季节和地区发生变化且与TC 强度的相关性较弱。一般情况下，TC 的风圈半径通常在海面风场风速达到34 节、50 节和64节时被观测记录到[13]，3 种半径分别对应于大风级、风暴级和台风/飓风级的TC强度。经过时空窗匹配之后，我们发现上述研究中34 节和50 节风圈半径的样本量分别为1 212和439，而64节风圈半径的样本量较少，这可能是由于ASCAT相邻观测刈幅之间相距较远减少了匹配的机会以及风场数据对实际风速的低估导致的。

考虑上述因素，本文选用R34来反映TC的结构特征和强度大小，并采用等方位角平均的方法基于ASCAT 海面风场计算TC 的34 节和50 节的风圈半径。具体来说，首先对最佳路径数据的风眼位置进行时间插值以确定ASCAT 风场对应时刻的TC 中心；其次，设定正负1节的风速阈值来绘制匹配风场的34 节和50 节风速等值廓线，结果见图4；然后，以时间插值确定的TC中心为准，将空间分为8个方位角（见图5a），通过空间双线性插值获取风速等值廓线上距离每个方位角最近两个点的连线与方位角的交点，并绘制风速-半径剖面（见图5b）；最后，计算各个交点与风眼的距离获得各方位角上的34 节和50 节风圈半径Di和Si（i=1，2，…，8），计算公式为：

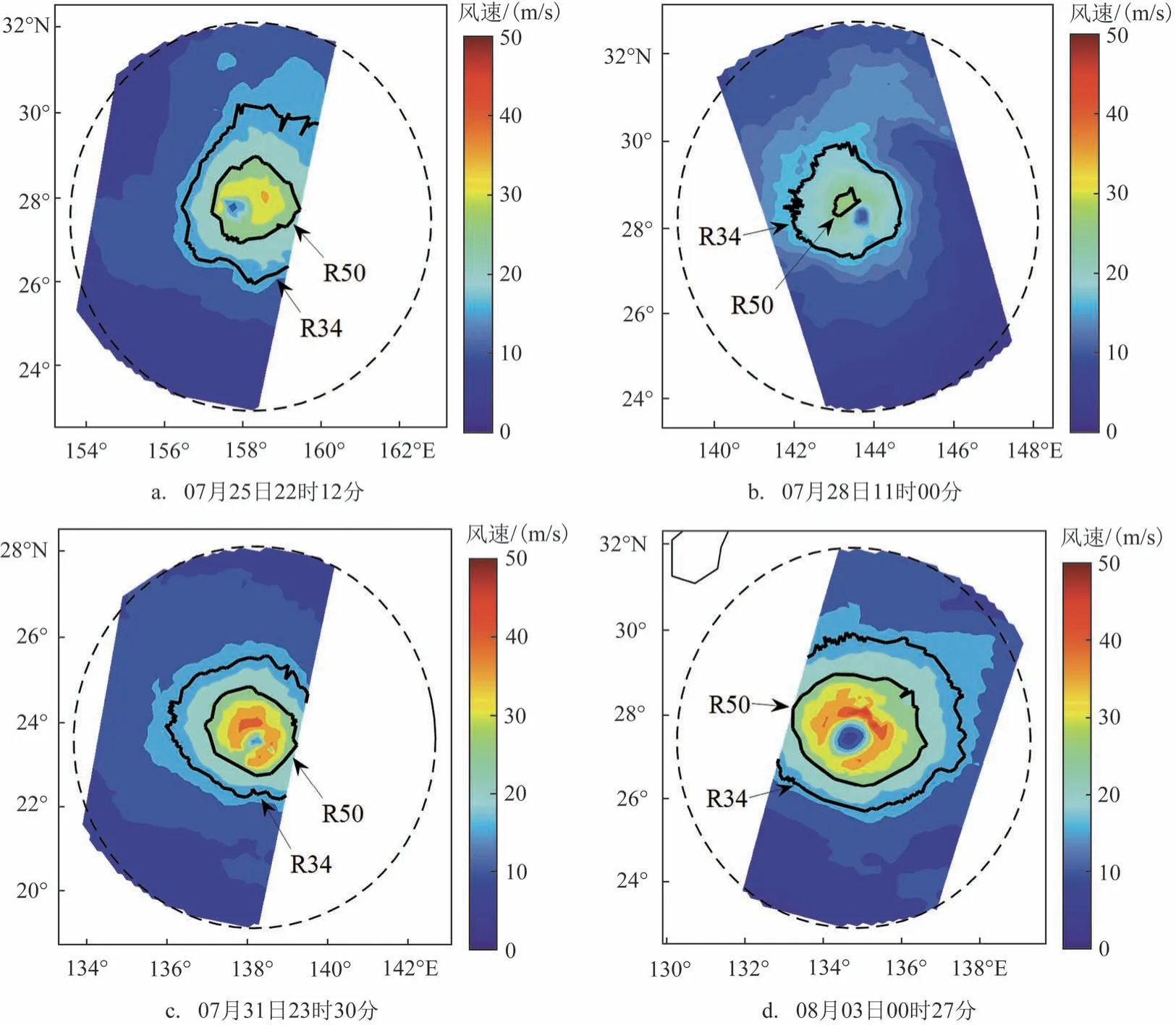
图4 台风“奥鹿”34节和50节风速等值廓线Fig.4 34-knot and 50-knot wind speed contour of Typhoon"Noru"

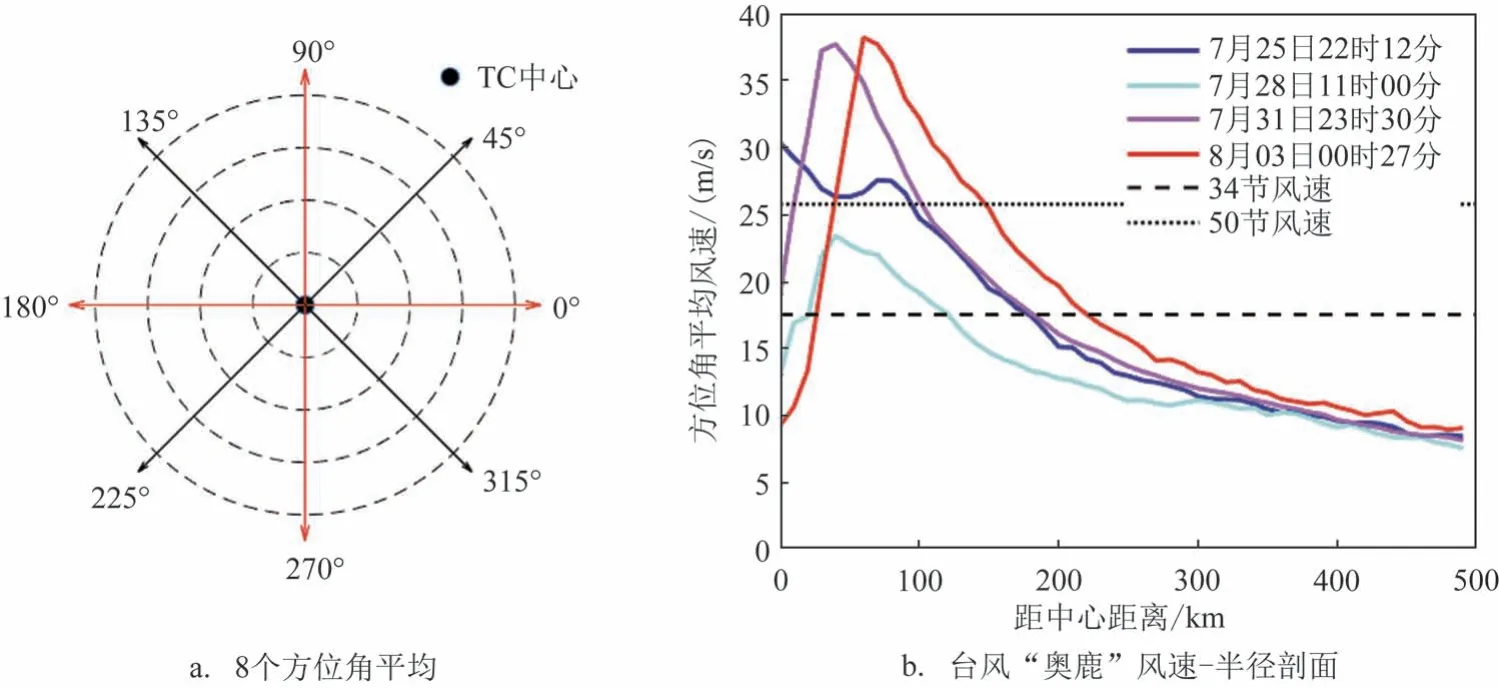
图5 R34和R50计算方法Fig.5 The method of calculating R34 and R50

式中：下标代表每个方位，将方位角进行平均后可得出半径计算公式，并用R34 和R50 表征该时刻TC尺度大小。

从图4 可以看出，TC 风场在实际情况下往往具有非对称特征，高风速区呈现不均匀分布，集中在环流某一侧，圆对称性结构较差，每个方位角的风圈半径是不相等的；当34 节风圈较大时，由于刈幅限制，等值廓线不闭合，部分方位角上的风圈半径无法计算；由于TC 风眼附近存在低风速区，一个方位角上存在多个符合风速阈值内的风速。

针对以上情况，我们优化了计算程序，将缺失的方位角半径设为缺测值，不计入方位角平均计算之中。真实环境下能够较完整呈现台风“奥鹿”结构的ASCAT 风场数据中的风速矢量往往是以离散格点形式分布的，这可能是由于雷达测量噪声引起风速廓线伪振荡导致的，所以通过设定阈值定义风速区间来绘制风场风速等值线的方法得到的廓线边缘是粗糙的，使用方位角平均将风速等值廓线圆对称化，可以消除大部分与TC 运动相关的不对称[16]，同时也便于后续的统计研究。

图5b 是台风“奥鹿”在4 个时刻各方位角风速随距离变化的风剖面曲线，在其生成和发展阶段，风速-半径剖面较为平坦；随着台风进入成熟阶段，其逐渐发展出风眼结构且逐渐增大，风速-半径剖面越来越陡峭，呈单“峰”分布且风速“峰”越来越突出。此时，34 节和50 节风速等值线出现多个交点，在计算各方位角上的风圈半径值时，需要排除风眼内的较小值，保留风眼外的较大值作为该方位角上的有效值。

2.4 比较方法

计算时空窗匹配所得TC 的R34 和R50 与对应最佳路径数据的观测值对比，采用偏差法、均方根误差法和相关系数分析法作为衡量比较结果的标准。计算公式为：

式中：Xi、Yi分别表示最佳路径数据中风圈半径的观测值和基于ASCAT 风场的计算值，i代表每个数据的编号，Xˉ、Yˉ分别对应于Xi、Yi数据集的均值；n为样本数。Bias 表示两个数据序列的偏离程度，正偏差表明计算值高于观测值，即高估，反之为负偏差，低估。RMSE 值始终为正且对异常值反映敏感，越接近0 表明计算方法越适用。CC 值表示两个序列的相关程度，CC=1 表示两变量完全线性相关，CC=0则表示两变量完全不相关，一般情况下，CC>0.8 表示两变量相关度较好。

3 结果与讨论

3.1 结果比较

基于第2 节的方法将NWP 和NA 海盆2013—2022年的5—11月的所有TC（见图1）结合在一起构建ASCAT 风场R34 和R50 数据集，并与最佳路径数据进行对比，结果见图6a 和6b。R34 和R50 的样本总数分别为1 212 和439，R34 和R50 的Bias 分别为8.6 km和-15.4 km，RMSE分别为52.4 km和39.6 km。ASCAT 观测的R34 比最佳路径大4.5%左右，差异误差约为12.3%；而ASCST 观测的R50 比最佳路径小约4.0%，差异误差约为25.4%，这个结果优于SOISUVARN 等[13]计算的R34 和R50 与最佳路径的比较结果，其对应的差异值和误差分别为3%、36%、28%和39%。

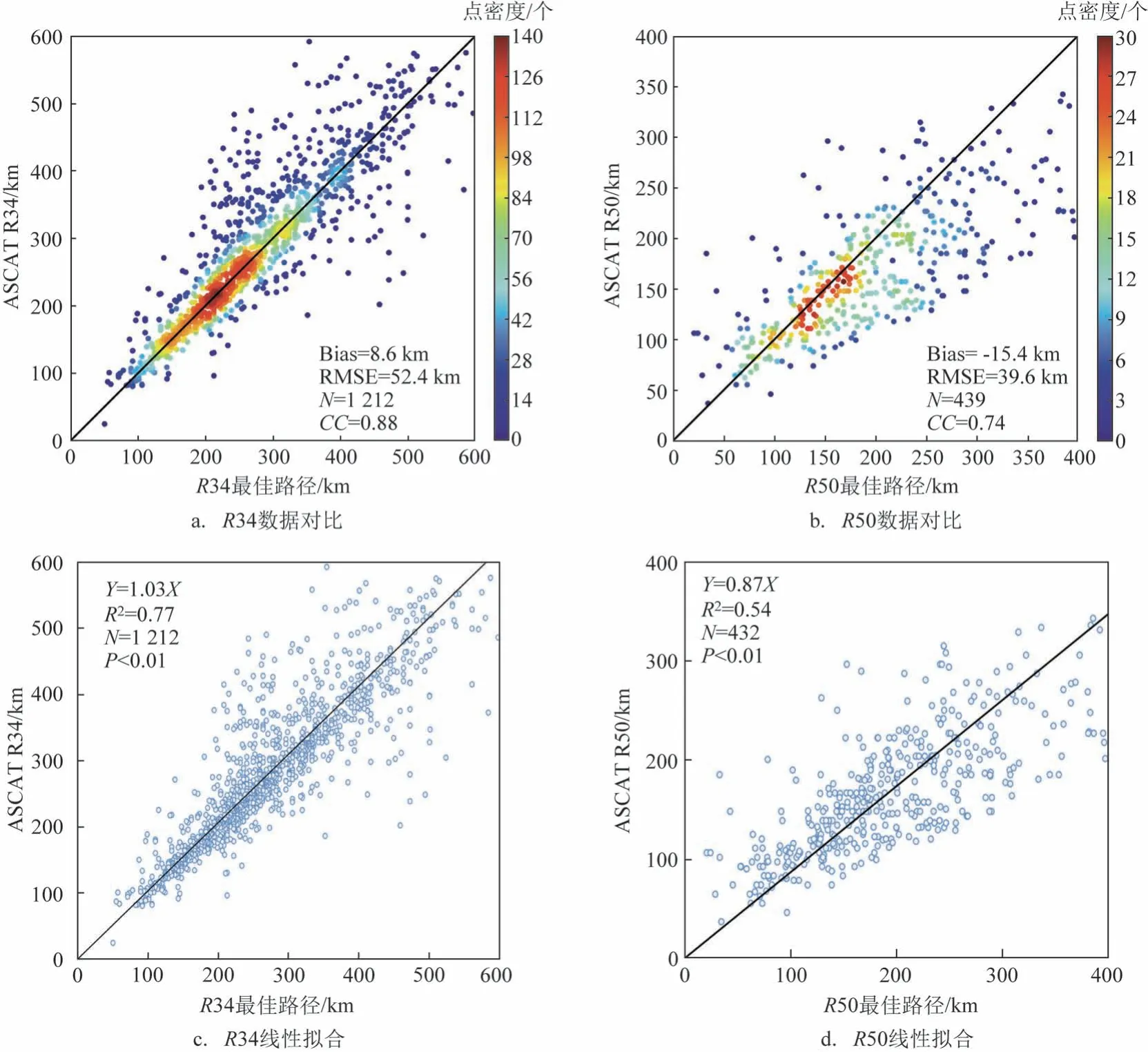
图6 最佳路径和ASCAT风圈半径统计比较Fig.6 Statistical comparison of R34 and R50 between Best Track and ASCAT data

ASCAT 估算的R34 和R50 与最佳路径数据的CC 值分别为0.88 和0.74（p<0.01），相关性较高。图6c和6d展示了ASCAT 风半径和最佳路径数据的线性回归结果，R34 和R50 的拟合关系分别为y=1.03x和y=0.87x，拟合模型的判定系数（R2）分别为0.77 和0.54，表明回归直线对最佳路径数据的拟合程度较好，且R34比R50的拟合结果更接近观测值，相关性更加显著。

由于Metop-A、Metop-B、Metop-C 是极轨卫星，在2.2 节时空窗匹配时也发现其在中低纬度的经过频率很低，ASCAT 对所有TC 样本的单日观测次数最多为1～2 次，且当TC 较大时，由于刈幅限制，ASCAT 通常只能观测到部分环流结构（在图4 中体现为34 节风速等值风圈不闭合），因此，对TC 结构不完整的风场进行方位角平均可能会引起R34 偏大；另一方面，由于ASCAT 对高风速存在低估[6]，这会引起强度达到风暴及以上的TC的50节风圈比真实情况小，因此R50呈现负偏差，以上可能是导致基于ASCAT 风场的计算结果与最佳路径存在差异的原因。

3.2 R34表征TC尺度

在2.3节中已提出用R34来反映TC的结构特征和强度大小，虽然C 波段ASCAT 对降雨相当不敏感，但是由于在高风速情况下风速数据存在不确定性，而且散射计测量的风速和最佳路径数据的时间尺度不一样，本节采用最佳路径的1 min 持续最大风速Vmax来表征TC 强度，检验与TC 大小相关的4个潜在相关环境变量（Vmax、纬度、TC 移动速度和风暴年龄）对ASCAT估算的TC风圈半径的影响程度，对这4 个参数和TC 风圈半径（R34 和R50）进行Pearson相关分析，结果见表1。

表1 NWP、NA和整个研究区TC风半径（R34、R50）与TC尺度相关环境变量之间的Pearson相关系数Tab.1 Pearson's correlation coefficients between TC wind radii（R34，R50）and TC size-related environmental variables in NWP，NA and the entire study area

结果表明，在这4 个参数中，最大风速与R34 和R50 的总体相关性最强（CC=0.36～0.66），与R50 在NWP 和NA 海盆中的估计（CC=0.36～0.48）相比，R34 与最大风速具有更强的相关性（CC=0.62～0.66）。在NWP 海盆中，纬度与风圈半径的相关性较小（CC=0.13～0.18），在NA 海盆中具有弱相关性（CC=0.25～0.26），同样在NWP中TC移动速度与风圈半径的相关性很小（CC=0.07～0.10），在NA 中相关性也较弱（CC=0.16～0.28）。值得注意的是，不同于纬度和TC 的移动速度，TC 风暴年龄与各海盆的风圈半径相关性增强（在NWP 的CC=0.28～0.33;在NA 的CC=0.35～0.37），KIM 等[17]认为这是由于TC风暴年龄与最大风速和纬度之间的相关性较强导致的。

以上结果表明，基于ASCAT 风场计算的R34变化趋势与最佳路径最大风速的变化趋势基本一致，这也说明了散射计的R34值比R50能够更好地表征TC 的影响强度和范围，因此，本文选用R34 值来反映TC 的结构特征和定义其强度大小（尺度）的方法是具有可行性的。此外，本文发现TC 的大小（R34）和其对应的强度之间存在明显正相关（CC=0.62～0.66），这与胡邦辉等[18]的结论相似，以上结果也体现了从ASCAT风场得到的风半径信息，在临近预报或短期预报方面对于分析TC 强度是有参考价值的。

3.3 TC大小分类和分布

2.3 节中已经介绍过，计算R34 和R50 时将研究的TC 都看作具有对称性，使用方位角平均将风速等值廓线圆对称化可以消除大部分与TC 运动相关的不对称。本节对2013—2022年的5—11月ASCAT探测到的NWP 和NA 海盆上的有效TC 数据进行分类，小型和大型TC 的分类节点采用R34 的均值（R）加减标准差（s）来定义，得到的值分别为1.54°纬度和3.51°纬度，因此将小于1.5°纬度的TC 归为小型，大于3.5°纬度的TC归为大型，中间为中型。

表2 总结了MERRILL[15]，日本气象厅（Japan Meteorological Agency，JMA）和联合台风预报中心（Joint Typhoon Warning Center，JTWC）以 及 梁 梅等[19]对TC 进行分类的结果，采用ROCI 分类和基于等值风速的平均半径进行定义的结果存在差异。本文对小型TC 的分类节点（1.5°纬度）与梁梅等（1.2°纬度）相近，由于ROCI会随季节和地区变化且与TC 强度的相关性较弱，因此MERRILL、JMA 和JTWC 对小型和大型TC 的分类结果偏大（分类节点约为3°纬度和5°～6°纬度）。

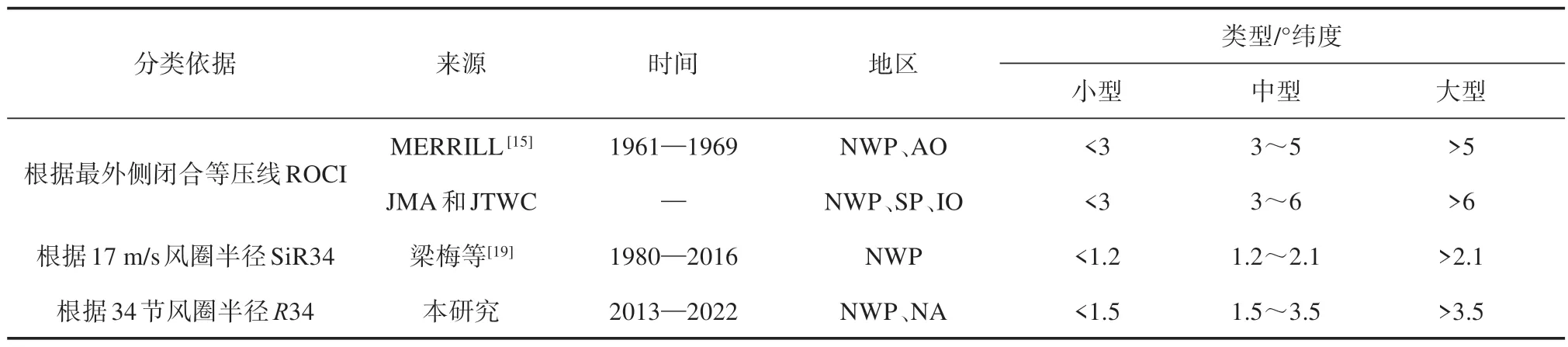
表2 不同研究人员和气象中心对TC大小的分类Tab.2 TC size categories used by different researchers and meteorological centers

图7为2013—2022年的5—11月NWP和NA海盆上ASCAT估算的R34月平均变化及标准差区间。标准差与月均值分布基本一致，两个海盆上平均尺度的峰值出现在9 月（NWP 的R34 为297.8 km）和10 月（NWP 的R34 为305.6 km; NA 的R34 为322.5 km），同时R34最大值均在10月（NWP的R34为591.9 km; NA 的R34 为575.4 km），之后11 月、5月、6 月呈下降趋势且NWP 的降幅更大，随着夏季临近（7月、8月），NWP的增长趋势平稳，而NA 的平均尺度低值出现在8 月（R34 为201 km），NWP 上月均值的最大值出现在10 月，与梁梅等[19]根据37 a（1980—2016 年）数据集分析得到的TC 尺度季节变化的结果一致。

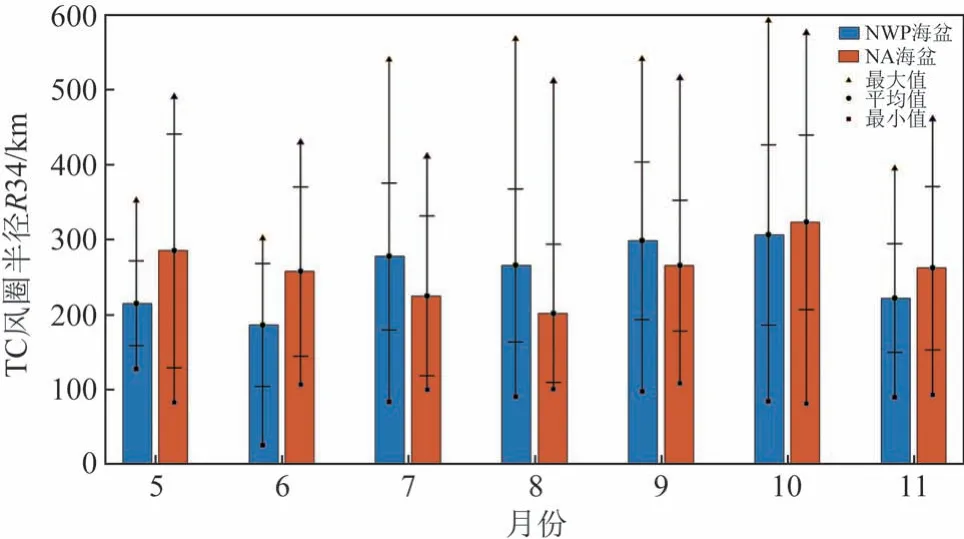
图7 2013—2022年ASCAT R34月平均变化趋势Fig.7 Monthly average variation trend of ASCAT R34 during 2013—2022

对ASCAT的TC数据进行大小分类的月分布结果见图8，其中中型TC 总数量最多，在NWP 和NA所占比重分别为68%和66.7%，NWP 的中型TC 主要分布在8—10 月，而NA 则集中分布在9—10 月。NWP 的大型TC 数量在7—10月呈显著增势且在10月达到峰值，其中9 月和10 月的数量超过小型TC，而NA的大型TC在9月和10月明显增长，10月出现峰值且数量超过小型TC。两个海盆上3 种类型TC的变化趋势总体均呈现单峰分布，小型和中型TC的峰值出现在9 月，大型TC 峰值滞后1 个月，但小型和大型TC 的总数相差不大，其在NWP 上分别为14.3%和17.7%，NA 上分别为17%和16.3%，这与LIU等[20]的研究结果一致。

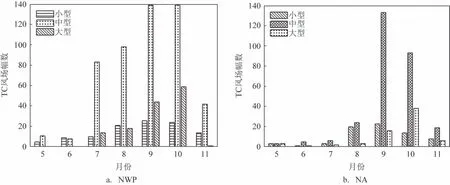
图8 2013—2022年两个海盆上ASCAT TC的3种类别的时间分布Fig.8 Time distribution of the ASCAT TC in three categories during 2013—2022 over the two basins

4 结论

本文基于ASCAT风场数据，采用了方位角平均估计TC 风场R34 和R50 的计算方法，探索了ASCAT 在研究TC 风圈半径的应用，并与最佳路径数据进行比较，同时对结果的误差做了分析，最后对西北太平洋和北大西洋上2013—2022年的5—11月的TC 大小进行分类和统计分析。主要结论如下：

①对于匹配的所有TC 样本，R34比最佳路径大4.5%左右，差异误差约为12.3%，R50 比最佳路径小约4.0%，差异误差约为25.4%；R34 和R50 的Bias 分别为8.6 km 和-15.4 km，RMSE 分别为52.4 km 和39.6 km，与最佳路径数据的CC 值分别为0.88 和0.74（p<0.01），相关性较高。与其他已有方法比较，结果表明本方法能够较好地估计TC风圈半径。

②在风圈半径与TC 大小潜在相关环境变量的相关性分析中，最大风速与R34 和R50 的总体相关性最强（CC=0.36～0.66），R34 与最大风速在NWP和NA 海盆中具有较强的相关性（CC=0.62～0.66）。ASCAT 散射计的R34 值比R50 能够更好地表征TC的结构特征和尺度大小，在临近预报或短期预报方面对于分析TC强度是有参考价值的。

③从2013—2022 年NWP 和NA 海盆上R34 的月平均变化趋势来看，TC 平均尺度的峰值出现在9月（NWP 的R34 为297.8 km）和10 月（NWP 的R34为305.6 km；NA 的R34 为322.5 km）；两个海盆TC分类的月分布结果表明，中型TC 的总数量最多，在NWP 和NA 所占比重分别为68%和66.7%，3 种类型TC 的变化趋势总体均呈现单峰分布，小型和中型TC 的峰值出现在9 月，大型TC 峰值滞后1 个月，但小型和大型TC的总数量相差不大。

由于需要将最佳路径记录和ASCAT 风场相匹配，受数据时空范围的限制，匹配案例数目较少。下一步的工作将使用更多源的数据集获取更多的匹配案例来验证和优化本文方法，同时拓展研究时间序列，建立TC尺度大小的气候学统计分析。

致谢：本文使用的ASCAT 近海岸风场数据由欧洲气象卫星组织（EUMETSAT）海洋与海冰卫星应用设施（OSI SAF）提供，本论文是第一作者本科毕业设计的部分内容，在完成本科毕业设计期间还得到张彪教授的建议和指导。本文是在原毕业设计的基础上经过进一步修改、补充、计算和扩充后完成，在此一并致谢。