倾斜角对独柱式变截面钢桥塔气动特性的影响∗

2024-01-05刘小兵姜会民于文文郑怡彤

振动、测试与诊断 2023年6期

关键词：桥塔来流倾斜角

刘小兵，姜会民，于文文，郑怡彤

（1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室石家庄，050043）

（2.河北省风工程和风能利用工程技术创新中心石家庄，050043）

（3.石家庄铁道大学土木工程学院石家庄，050043）

引言

变截面倾斜桥塔由于具有更好的视觉效果和通航适应能力，被越来越多地应用于实际工程中。风流经此类桥塔时往往会表现出较为复杂的三维流动效应，其气动特性与等截面竖直桥塔相比有很大的不同。仅按照等截面竖直桥塔的气动特性对变截面倾斜桥塔进行抗风设计，可能会由于对风荷载的不合理取值导致桥塔抗风性能不足或建筑材料的浪费。因此，准确掌握变截面倾斜桥塔的气动特性对其抗风设计具有重要意义。

对于截面沿塔高差异不明显的等截面竖直桥塔，可依据条带假设采用节段模型风洞试验或二维数值模拟的方法研究其气动特性，此类研究十分广泛［1-5］。对于截面沿塔高差异明显的变截面倾斜桥塔，不能把桥塔气动特性的研究简化为二维问题，需要考虑三维效应的影响。文献［6-8］讨论了变截面竖直桥塔的气动特性。与变截面竖直桥塔相比，变截面倾斜桥塔气动特性的研究更为少见。李永乐等［9］测试了一座倾斜角（桥塔与竖直方向的夹角）为25°的独柱式变截面桥塔在不同风向角下的整体气动力系数，并推算了阻力系数沿桥塔高度的变化规律，发现倾斜改变了桥塔的整体气动力，同时也改变了气动力沿塔高的分布状况。Marra 等［10］以一座倾斜角为38°的变截面桥塔为对象，对比分析了全桥塔模型和桥塔节段模型的风洞试验结果，研究发现，桥塔节段模型得到的阻力系数较全桥塔模型高出50%左右。

目前，针对变截面倾斜桥塔并考虑三维效应的研究较少，研究对象一般为特定倾斜角的桥塔，不同倾斜角对桥塔气动特性的影响规律尚不明确。鉴于此，笔者以国内某座拟建的独柱式变梯形截面倾斜钢桥塔为工程背景，进行了一系列全桥塔刚性模型测压风洞试验，对比分析了不同倾斜角下桥塔各截面的气动力系数和斯托罗哈数随风向角的变化规律。研究可为倾斜变截面桥塔的风荷载取值和风致振动分析提供参考。

1 工程背景

该桥位于海南省三亚市，为跨越人工河航道而建，是一座独柱式钢斜塔斜拉桥。桥梁全长为233.4 m，主跨为98.8 m。桥塔高为73.6 m，顺桥向倾斜，倾斜角为30°。塔柱截面是底角为60°的等腰梯形，截面尺寸沿塔高非线性地先变大后变小，其中塔柱底端截面的底边边长为2.7 m，塔柱顶端截面的底边边长约为0.2 m，整体呈现出鱼腹形，桥塔构造图和测点布置如图1 所示。

图1 桥塔构造图和测点布置 (单位：m)Fig.1 Structure diagram and pressure tap arrangement of bridge tower (unit:m)

当地风环境较为恶劣，基本风速高达37.3 m/s。与钢筋混凝土桥塔相比，钢桥塔由于具有更小的刚度和更低的阻尼，在风的作用下易发生涡激共振现象。因此，对此桥塔的气动特性进行了分析研究。

2 试验概况

根据《公路桥梁抗风设计规范》［11］对阻塞率的要求，采用ABS 板以1∶70 的缩尺比严格按照原桥塔的几何外形制作了全桥塔刚性模型。根据塔柱截面变化的剧烈程度，在塔柱表面非等间距地布设了5圈测点，每圈10 个测压孔，测点截面中心距离地面的高度分别为16.7，34.5，49.2 ，64.9 和72.7 m（图1）。为方便描述，定义s为测点截面距塔柱底端的距离与塔柱总长的比值，5 圈测点由下到上s依次为0.16，0.40，0.60，0.81 和0.92。全桥塔刚性模型测压风洞试验在石家庄铁道大学STU-1 风洞低速试验段内进行，该试验段宽为4.4 m，高为3.0 m，长为24 m，最大风速为30 m/s。模型底端固定在转盘上，通过计算机控制转盘旋转来精确改变风向角，风洞试验如图2 所示。

图2 风洞试验照片Fig.2 Photograph of wind tunnel test

通过张拉钢丝和在模型内部布置多道纵肋的方式来保证模型的刚度，确保模型不发生明显的位移和变形。在试验过程中模型仅发生轻微抖动，不存在较大幅度的振动响应。风压测量以及数据采集采用电子压力扫描阀和DTC Initium 数据采集系统，扫描阀采样频率为330 Hz，连续采样时长为30 s。本研究用到的仪器还有皮托管（用于测量来流风速）和高精度数显水平尺（用于测量桥塔倾斜角）。

根据项目工程所在地的地形地貌及桥梁周围的建筑环境，确定远方来流为A 类风场，采用尖劈、粗糙元和格栅被动模拟方法进行风剖面模拟，地面粗糙度模拟装置如图3 所示，采用该装置得到的平均风速剖面和紊流度剖面如图4 所示。可以看出，风速剖面与理论风剖面吻合较好。

图3 地面粗糙度模拟装置Fig.3 Simulator of terrain roughness

图4 平均风速剖面和紊流度剖面Fig.4 Mean wind velocity profile and turbulence intensity profile

试验风速为16 m/s，风向角α的定义如图5 所示。以顺桥塔倾斜方向为0°风向角，由于对称性，风向角的变化范围为0°~180°，变化步长为5°，共进行37 个风向角的测试。为了研究桥塔倾斜角度对气动特性的影响，变化原桥塔倾斜角β为0°，10°，20°及40°，分别进行了测试。

图5 风向角定义Fig.5 Definition of incidence angle

3 桥塔的气动力特性

定义体轴系下桥塔阻力系数CH、升力系数CV分别为

其中：FH，FV分别为由桥塔表面压力积分得到的单位长度的顺桥向阻力和横桥向升力。

试验参数定义如图6 所示。需要说明的是，本试验的测试截面始终与桥塔轴线垂直，当桥塔倾斜时气动力系数所在平面与来流方向呈现出不平行的特点，这与常规节段模型试验有所不同。

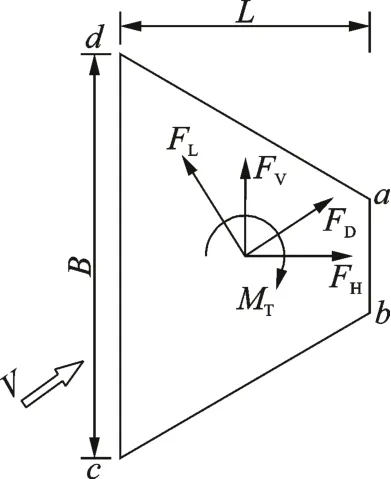
图6 试验参数定义Fig.6 Definition of test parameters

定义风轴系下桥塔阻力系数CD、升力系数CL分别为

其中：FD，FL分别为由桥塔表面压力积分得到的单位长度的顺风向阻力和横风向升力。

定义扭矩系数CM为

其中：MT为由桥塔表面压力积分得到的单位长度的扭矩。

图7 为不同风向角下桥塔的气动力系数（体轴坐标系，定义分别见式（1）、式（2）和式（5））。可以看到，当桥塔处于竖直状态时（β=0°），各截面的气动力系数相差不大，而桥塔不同高度位置截面的几何尺寸有所差异，且对应的风速也不一样，这说明竖直桥塔气动力系数的三维效应不明显。

图7 不同风向角下桥塔的气动力系数Fig.7 Aerodynamic force coefficients of bridge tower at different incidence angles

1）当α=0°~35°时，竖直桥塔各截面的阻力系数基本不随α的变化而变化，其值稳定在1.75 附近。升力系数随α的增大由0 缓慢减小至-0.4 左右；扭矩系数则由0 逐渐增大至0.12 左右。

2）当α=35°~180°时，随着α的增大，阻力系数先由1.75 附近减小到-1.0 左右，然后在该值附近波动；升力系数表现出了先增大后减小的规律，最大值发生在α=105°~150°范围内，其值约为2.0；扭矩系数表现出了先减小后增大的规律，最大扭矩发生在85°附近，扭矩系数约为-0.25。这些结果可为此类截面柱体结构的抗风设计提供参考。

当桥塔处于非竖直状态时，各截面气动力系数随α的变化规律与竖直桥塔较为类似。由于三维效应，桥塔不同高度截面的气动力系数在一定风向角范围内表现出了明显差异。

1）阻力系数绝对值在α=0°~35°风向角范围内随s的增大而逐渐减小，在α=90°~180°风向角范围内随s的增大而逐渐增大。当α为0°和180°时，各截面阻力系数的差异最为明显。随着α的增大或减小，这种差异表现出了逐渐减弱的趋势。

2）升力系数和扭矩系数绝对值在α=35°附近随s的增大而减小，在α=140°附近随s的增大而增大。在这两个风向角附近，与桥塔下部（s为0.16 和0.40）相比，桥塔上部截面的气动力系数随塔高递增的规律更为显著。

3）当α=35°~90°时，桥塔各截面的气动力系数相差不大，并与竖直桥塔的气动力系数接近。这说明当α=35°~90°时，气动力系数的三维效应不明显。对比不同倾斜角下桥塔的气动力系数可以发现，随着桥塔倾斜角度的减小，各截面气动力系数的差异逐渐减小，这说明气动力系数的三维效应逐渐减弱。

α=0°（顺桥塔倾斜方向来流）和α=180°（逆桥塔倾斜方向来流）时不同倾斜角下桥塔的阻力系数如图8 所示。由图可以看出，桥塔不同截面的阻力系数随倾斜角的变化规律明显不同。

图8 α=0°和α=180°时不同倾斜角下桥塔的阻力系数Fig.8 Drag coefficients of bridge tower at different inclination angles when α=0° and α=180°

1）由图8（a）可知，顺桥塔倾斜方向来流时，截面s=0.60，0.81 和0.92 的阻力系数随倾斜角的增大而减小，截面s=0.16 和0.40 的阻力系数随倾斜角的增大表现出先略有增大后逐渐减小的规律，在β=20°附近达到最大值，两截面的最大阻力系数分别为竖直桥塔的1.02 和1.10 倍。

2）图8（b）可知，逆桥塔倾斜方向来流时，截面s=0.81 和0.92 的阻力系数绝对值随倾斜角的增大表现出先增大后减小的规律，最大值同样发生在β=20°附近，两截面的最大阻力系数绝对值分别达到了竖直桥塔的1.25 和1.39 倍。截面s=0.16 和0.40 的阻力系数绝对值随风向角的增大则表现出逐渐减小的规律。

3）与其他截面相比，接近中间位置的截面（s=0.16）的阻力系数随倾斜角的变化较为平缓。

综上可知，桥塔倾斜会使桥塔受到的气动阻力呈现出沿高度分布不均匀的特点。当顺桥塔倾斜方向来流时，倾斜会使桥塔上部截面的阻力减小，使桥塔下部截面的阻力增大。当逆桥塔倾斜方向来流时，倾斜会使上部截面的阻力增大，使下部截面的阻力减小。倾斜对桥塔阻力的放大效应在β=20°附近最为明显，因此在进行桥塔设计时，宜避开此倾斜角。实际上，倾斜桥塔受到的气动力在α=30°和140°附近也表现出了类似的规律。当α=30°时，倾斜会使桥塔上部截面受到的气动力减小，使桥塔下部截面受到的气动力增大。当α=140°时，倾斜会使桥塔上部截面受到的气动力增大，使桥塔下部截面受到的气动力减小。文献［12］以等截面方形断面柱体为对象，研究了升力系数随倾斜角的变化规律，得到了与本研究试验类似的规律。

为了给实际工程取值提供参考，笔者对α=0°和α=180°时桥塔各截面阻力系数随倾斜角的变化曲线进行了三次多项式拟合，各截面阻力系数的拟合效果见图8，阻力系数拟合公式各项系数见表1。拟合公式为

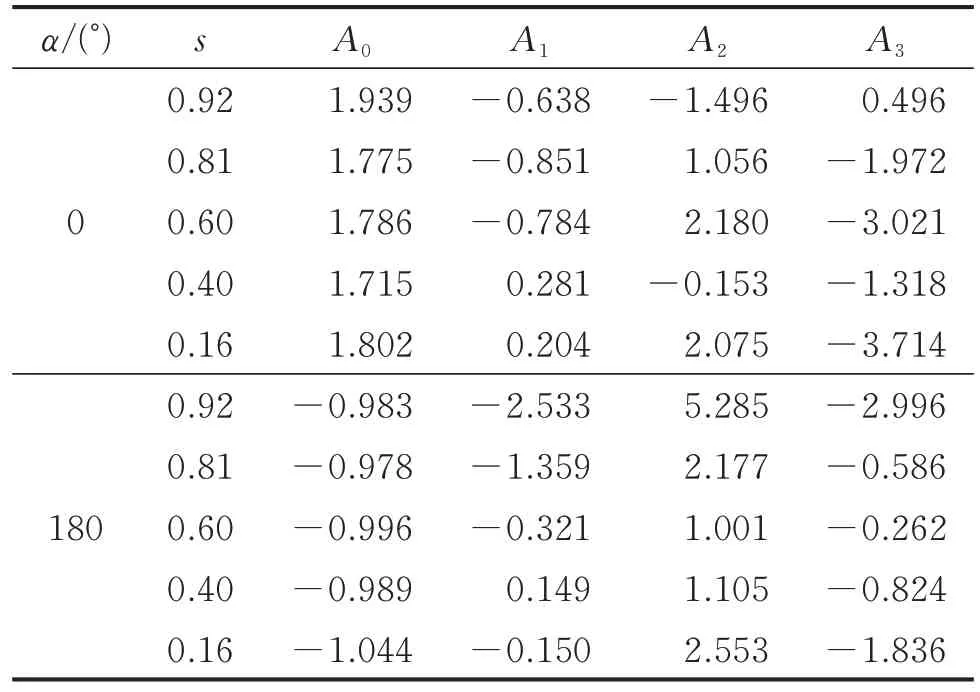
表1 阻力系数拟合公式各项系数Tab.1 The coefficient of fitting formula for drag coefficient

其中：β为倾斜角（弧度制）；A0，A1，A2和A3为三次多项式各项系数。

4 桥塔的旋涡脱落特性

定义无量纲参数斯托罗哈数St 来反映桥塔的旋涡脱落特性

其中：f为旋涡脱落频率，可由风轴坐标系下的升力系数时程经过傅里叶变换获得。

α=0°时原桥塔风轴系升力系数时程如图9 所示。可以看到，风轴系升力系数始终在0 附近波动。随着s由0.92 减小到0.16，风轴升力系数波动的幅度呈现出逐渐增大的趋势。

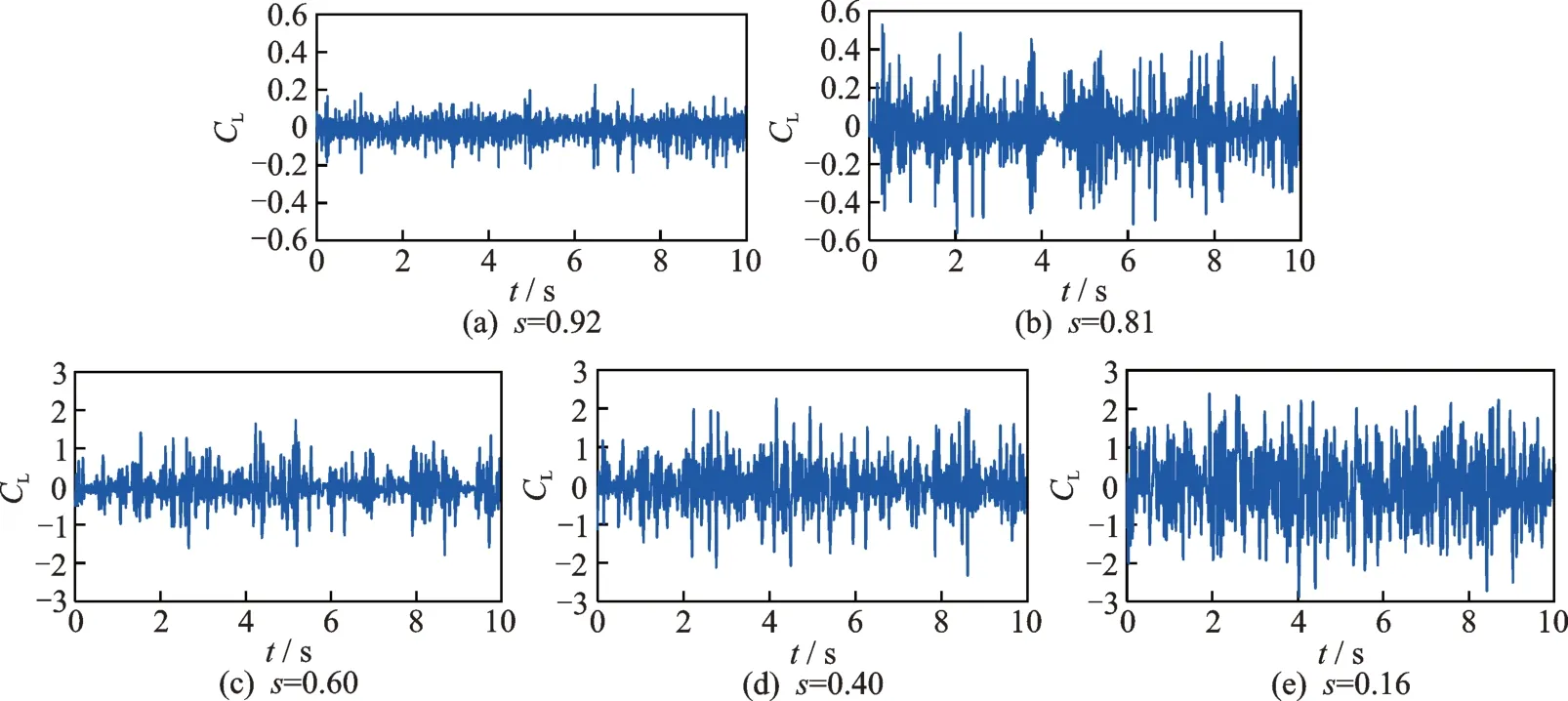
图9 α=0°时原桥塔风轴系升力系数时程Fig.9 Time history of lift coefficient in wind shafting of original bridge tower when α=0°

α=0°时不同倾斜角下升力系数傅里叶幅值谱如图10 所示，分别为无倾角（β=0°）、中等倾角（β=20°）和大倾角（β=40°）情况。可以看到，幅值谱图中频率成分较多，这可能是由前方来流的紊流（A 类风场）成分引起。截面s=0.92 和0.81 的卓越频率较不明显，说明这两个截面未表现出明显的旋涡脱落现象，这可能与端部效应有关。当β=40°时（图10（c）），桥塔各截面均未表现出明显的卓越频率，这表明随着倾斜角的增大，由于三维效应的增强，桥塔各截面旋涡脱落会变得不明显。

图10 α=0°时不同倾斜角下升力系数傅里叶幅值谱Fig.10 Fourier amplitude spectra of lift coefficient at different inclination angles when α=0°

不同风向角下桥塔的斯托罗哈数如图11 所示。由图可以看出：截面s=0.92 在所有工况下均未表现出明显的旋涡脱落现象，只有当α在0°和120°附近的一定风向角范围内时，桥塔其他截面才会表现出较为明显的旋涡脱落，而这一风向角范围随着截面高度的变化而变化；随着s由0.92 减小到0.16，这一风向角范围呈现出逐渐扩大的趋势；当s=0.16 时，风向角范围最大，为α=0°~30°和α=90°~150°；桥塔各截面的斯托罗哈数随倾角变化不大，当α在0°附近一定风向角范围内时，各截面的斯托罗哈数在0.11 附近波动；当α在120°附近一定风向角范围内时，各截面的斯托罗哈数在0.15 附近波动。另外，当α=0°时，来流与桥塔截面的底边垂直；当α=120°时，来流与桥塔截面的腰垂直。