具有横向坡度的阶梯式溢洪道水流消能应用分析

杜为彬

（广东琮泰工程有限公司，广东 雷州 524200）

0 引 言

在正常的洪水事件中，水库中过多的水通常会通过溢洪道排出。然而，在极端情况下，由于一些现有旧大坝的溢洪道容量不足，可能会在坝体上发生洪水漫顶[1]。对于堤坝，通常不允许出现漫顶，漫顶可能会侵蚀大坝的下游面，危及大坝的安全或造成灾难性的破坏[2-3]。因此，需要对这些大坝进行修复。

大坝修复最有效的方法之一是漫顶保护系统，漫顶保护系统通常用于覆盖大坝顶部及其下游面[4]。这样可以有效地提高坝体的泄洪能力，从而安全地排放极端洪水。目前，已有几种漫顶保护系统如铺路、加筋土、阶梯重叠混凝土块、阶梯石笼和碾压混凝土。然而，最常见、最有效的漫顶保护系统是阶梯式的保护系统[5-6]。除了侵蚀保护外，阶梯式保护系统还具有其他几个优点，如施工经济（使用碾压混凝土可减少财政支出，缩短施工时间）、降低空化风险、流动曝气以及由于台阶而产生的显著能量耗散，这反过来可能会导致溢洪道坡脚处消能结构的尺寸显著降低。阶梯式保护系统由一系列连续的台阶组成，这些台阶建造在从顶部到坡脚的下游斜坡上。

为了提高覆盖在路堤台阶上水流的能量耗散，文章研究了几种台阶形状和配置，台阶具有横向坡。具有横向坡度的台阶从一个桥台或溢洪道墙向另一个桥台或溢洪道墙呈Z 字形倾斜。文章探讨了阶梯式溢洪道台阶的横向坡度对阶梯式溢洪道水流特性的影响。

1 实验装置与步骤

试验是在水力学实验室的矩形刻痕壁（10 mm厚）水槽中进行的。水槽长8m，宽0.605m，有两个深度：前2.5m 长度的水槽深度为1.35m，其余部分长度为5.5m，深度为0.70 m。水流由一个大型进水池供应，该进水池通向水槽上游的一个钢制蓄水池（一个消力池）。

为了本研究的目的，三个物理模型由木材（中密度纤维板MDF）制成。每个模型由一个宽顶堰（宽0.605 m，长0.60 m，上游有尖角）和16级台阶组成。台阶高度与台阶长度之比为1V∶2H（h=0.06m，l=0.12m）；阶梯式溢洪道段的坡度（θ）为26.6°。三个梯级溢洪道中有两个配备了平台阶和非平台阶的组合。不平坦的台阶是具有横向坡度的台阶。具有横向坡度的台阶是指从一个桥台或溢洪道墙向另一桥台或其他溢洪道墙呈Z 字形倾斜的台阶。本研究中使用的阶梯式模型草图如图1 所示。对于第一个模型，M1 配置，所有16 个阶梯均保持平坦，作为参考模型。对于其他两个模型，M2 和M3 配置，在第一级台阶之后，对12 个台阶给出了不同的横向坡度。由于坝顶不能有横向坡度，所以第一级台阶保持平坦。最后三级台阶也保持平坦，以减少脚趾处产生的倾斜跳跃的影响。对于M2 和M3 配置，台阶高度在水槽中发生变化；对于M3配置，台阶高度从0.06 m 变为0；对于M2 配置，台阶高度从0.06 m 变为0.03 m（见表1）。

表1 实验工作中使用的配置总结

木质阶梯式模型的长度为2.52 m，刻痕侧壁和水平刻痕倒置水槽位于下游大型钢制水箱中，水从该水箱泵送至上游供水池。该泵提供的恒定排水量高达0.05 m3/s。使用位于进水管中的超声波流量计（0.00 025～0.065 m3/s）测量排放流量。水槽和其他设施的示意图，如储罐、再循环罐、泵、超声波流量计、点式仪表和阀门，如图2 所示。

图2 实验装置的示意图

宽顶模型上游和水跃下游的水流深度使用精度为1 mm 的指针式仪表进行测量。第一个测点仪位于模型上游0.6 m 处。第二个测点仪位于水跃下游，用于测量水跃的后续深度。在产生水跃后，模型下游的水深通过在水槽末端放置木槛来控制。水跃的位置尽可能靠近模型的脚趾（距离最后一个台阶20cm）。

2 结果与分析

实验中收集数据点和6～8h 的视觉观察。记录了250 多个单独的数据（流量、3 个位置的排放量、水深、起始点位置和水跃长度），并拍摄了照片和录像带。

2.1 流动特征

对于阶梯式溢洪道上的水流，可以通过目视观察来区分流型和流。对于本研究，在小流量下，阶梯式模型上的水流为推覆流类型。推覆流是一种流动类型，其特征是一系列自由落体射流流过台阶；从上台阶落下的水撞击下台阶的踏板，形成或不形成水跃。对于M1 配置，当yc/h＜ 0.63 时，可以观察到推覆流状态，其中yc是临界流动深度，h是台阶高度。矩形渠道中溢洪道上水流的临界深度可通过yc=(qw2/g)1/3计算得出，其中是单位宽度的排水量，g是重力加速度。对于M2 配置，当yc/h＜0.98 时，推覆流态占主导。而对于M3 配置，当yc/h＜1.1 时，推覆流态占主导。

另一方面，在大流量的情况下，会出现撇渣流。在撇渣流中，水像厚层一样在台阶边缘形成的伪底部（倒置）上流动。此外，文章发现撇渣流中水面的波动并没有反映潜在的台阶模式。对于M1 配置，观察到yc/h≥0.87 时的撇渣流型。然而，对于具有横向坡度的M2 和M3 配置的台阶模型中获得的较大yc/h下可以观察到撇渣流型。对于M2 配置，在yc/h＞1.2 时出现撇渣流型。而对于M3 配置，即使yc/h=1.37 也未观察到撇渣流，本研究中使用的最大流量。

根据文献，对于θ=26.6°的阶梯式溢洪道，当流水下的阶梯完全淹没时，通常会发生撇渣流。此外，在撇渣流中，通常在台阶内部形成具有涡流模式的水再循环。对于M2 和M3 配置，当yc/h＞1.2 时，在自由落体射流下方所有台阶的内部都会积水。然而，在一些排放处，当射流部分击中台阶（接近台阶末端）且流水下的台阶部分充满时，会出现过渡状态。当Qw＞ 0.036 m3/s 时，满足撇渣流型的要求。在一些中间排放处，观察到了具有强烈飞溅的混乱行为。这种类型的流被归类为过渡流。

一般来说，带有横坡台阶（M2 和M3 配置）的溢洪道沿线的流动条件非常湍流。自由表面非常不规则，有许多横波。这反过来又导致了在M2 和M3 配置上形成更厚的流动。因此，在相同的流速下，沿M1 的流量膨胀似乎小于M2 和M3 配置；与M1配置上的流动水相比，M2 和M3 配置下流动水的空气-水混合更强。这可能是由于气流、台阶和自由表面内的再循环涡流之间的强烈相互作用，从而导致大量空气进入主流[7-8]。

2.2 起始点的位置

对于所有配置，掺气流通常在低流量时非常接近坝顶的位置。然而，随着流量的增加，掺气流出现在上部几个台阶之后，并随着流量的增大而稳定增加。对于非掺气区域，流动表面清澈透明。然而，在台阶空腔引起的湍流（湍流边界层）到达流动水表面的那几个台阶之后，发生了显著的曝气。到达湍流边界层和自由表面的位置称为起始点。超过起始点后，空气开始夹带并渗透整个膨胀的流动深度。然而，在初始点之前，空气夹带通常归因于侧壁和表面纵向涡流形成的湍流。

对于本研究中研究的3 个模型，起始点的位置被确定并测量为从第一步边缘到自由表面曝气开始的纵向距离。起始点被区分为流动水从透明的玻璃状外观转变为流动水表面夹带空气的泡沫状外观的位置。为了量化台阶横向坡度对起始点位置的影响，实验结果显示在图3 中的无量纲结构中，利用无量纲项Li/ (h·cosθ)作为无量纲流量yc/h的函数，式中，Li是从第一级台阶边缘到掺气区和非掺气区之间分隔线的估计纵向距离，θ是穿过台阶边缘的直线与水平面之间的角度θ=26°，h是台阶高度。建立了yc/h≥0.8 的关系。

从结果来看，与M2 和M3 配置的相应长度相比，M1 配置的非掺气区域的长度更大。从图3 中可以看出，对于相似的yc/h，M2 配置的Li值减少到M1 配置的1/3（平均值），即33%；而M3 配置的Li值减少到大约一半（平均值），即48%。这归因于台阶横向坡度的影响。阶梯的横向坡度呈Z字形，在水槽和横波中形成了不均匀的速度分布条件。此外，侧壁形成的波浪会使靠近墙壁的水面略微升高，波浪可以从墙壁上落下或滚入主流。因此，这就产生了一个充满横波的极度动荡、高度不规则的自由表面。这反过来又导致自由表面上流动水的泡沫外观与第一台阶边缘的距离减小，Li值减小。

2.3 能量耗散

一般来说，阶梯式溢洪道上水流的能量耗散可通过阶梯式溢洪道上的能量损失ΔH占阶梯式溢洪道顶部总水头的比例进行估算。阶梯式溢洪道上方的ΔH等于阶梯式溢洪道顶部可用的总水头（最大水头）Hmax与阶梯式溢洪道坡脚处剩余水头Hres之间的差值。非阶梯式溢洪道顶部的最大可用水头可从以下公式获得：，其中Hdam为坝高，yc为流经阶梯式溢洪道的临界水深。Hres可表示为：，其中yw为清水深度，qw为单位长度流量，α为能量修正系数，能量修正系数在1.01 到1.13 之间。在本研究中，α取平均值1.07。Hres也称为剩余能量或留在溢洪道坡脚处的能量，对溢洪道下游消能结构的设计非常重要。Hres的动力部分通常在溢洪道坡脚处消力池的水跃中消散。

为了量化阶梯式模型的能量耗散，本研究中获得的数据关系采用无量纲项作为无量纲流量yc/h的函数，如图4 和图5 所示。尽管对于M2 和M3 配置，台阶高度在水槽中发生变化，但在本研究中，在构建所有关系时，考虑了0.06 m（h=0.06 m）的台阶高度。

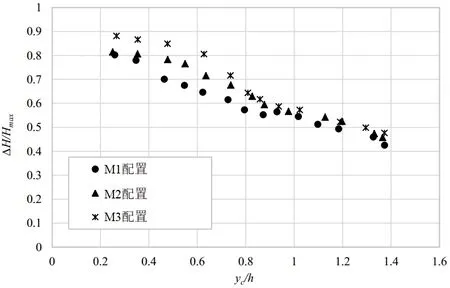
图4 不同步骤配置下的能量耗散作为 的函数比较（θ =26°）

图5 不同步骤配置下的相对能量损失和相对临界流深（θ =26°）

从图4 可以看出，对于3 个阶梯式模型，由台阶引起的能量耗散主要取决于yc/h比值，阶梯模型的能量消耗量随yc/h比值的增大而减小。此外，从结果比较可以看出，与预期的一样，在0.25＜yc/h＜ 1.4 的条件下，在所有排放过程中台阶具有横坡的模型能量耗散更高。从图5 可以看出，对于所有排放，M2 配置的能量耗散比M1 配置高7% 。对于 M1 和M3 配置，M1 和M3 配置之间的能量耗散百分比差异为6%～14%，平均值为11% 。

以上结果可以解释为：大部分流动发生在具有横坡台阶的模型上，为推覆流。在推覆流态中，水作为一系列自由落体射流从上部台阶向下移动到下部台阶。推覆流态中的动能通常通过冲击、混合和破碎台阶上的射流，以及在台阶上形成部分或完全形成的水跃而消散。对于M2 和M3 配置中，台阶的横向坡度增强了射流冲击、破碎和混合；台阶的坡度增加了台阶高度并形成了横向流。换句话说，台阶的横向坡度会产生尾迹，从而产生更大的流动阻力。因此，与具有平坦坡度的模型相比，具有横向坡度的模型上的流动具有更高的能量耗散。

3 结 论

文章对具有横向坡度的阶梯式溢洪道的流动特性进行了实验研究。研究的重点是纵向坡度（θ）为26.6°的阶梯式溢洪道的消能性能，这是堤坝的典型坡度。在具有平坦台阶的阶梯式溢洪道上，可能会出现3 种流态：推覆流、过渡流和撇渣流。然而，在具有横向坡度的阶梯式溢洪道上，可能只出现2 种类型的水流：推覆流和过渡流。

1）台阶的横向坡度减少了起始点与第一台阶边缘的距离（起始点位置）；对于具有5.7°横向坡度的台阶模型，起始点与第一台阶边缘的距离减少了48%。

2）对于具有横坡台阶的模型，临界深度（yc）与台阶高度（h）的比值（＞1.37）较高时，出现撇渣流。此外，能量耗散计算表明，能量耗散率随台阶横向坡度的增加而增加。

3）对于给定的台阶横向坡度，能量耗散率随着流量的增加而降低。最大的能量耗散发生在具有最大横向坡度（5.7°）台阶的溢洪道上。然而，对于较高的流量排放，能量耗散率略低。