珠江区重点流域水资源承载状况比较研究

金占伟,孙 波,刘和昌

(1.水利部珠江水利委员会珠江水利综合技术中心,广东 广州 510611;2.水利部珠江水利委员会技术咨询(广州)有限公司,广东 广州 510611)

水资源是基础性自然资源和战略性经济资源[1],在保障经济社会发展和维持生态环境平衡中具有不可替代作用。水资源承载力是指某一地区水资源在某一具体历史发展阶段下,以可以预见的技术、经济和社会发展水平为依据,以可持续发展为原则、以维护生态环境良性循环发展为条件,经过合理优化配置后,对该地区社会经济发展的最大支撑能力,其已成为衡量一个地区或流域可持续发展程度的重要指标之一。

水资源承载力研究最早始于20世纪70年代,国际有关组织针对资源匮乏国家的土地、水等资源承载力进行研究,提出了水资源承载力的相关概念[2]。在中国,水资源承载力的概念由施雅风等[3]于1989年首次明确提出,随后有关水资源承载力的研究成果不断完善和丰富[1-2,4-26]。目前,水资源承载力研究主要包括水资源承载力内涵及基础理论研究、评价方法与评价指标体系研究、典型区域实证研究等。王建华等[4]从水量、水质、水域空间和水流状态4个维度赋予了水资源承载力新的内涵,并基于新内涵构建了“四层三级”评价指标体系。朱一中等[8]指出可持续发展理论、水-生态-社会经济复合系统理论、二元模式下的水文循环机制和过程是水资源承载力研究的理论基础,对水资源承载力研究的基本内容、评价指标体系的建立和评价方法进行了较为全面的概况和总结。左其亭[9]在梳理中国水资源承载力研究的发展历程和研究方法对比分析的基础上,对水资源承载力计算分析方法进行了归纳总结,指出水资源承载力定量计算方法主要有经验公式法、多指标综合评价法、系统分析法等,而水资源承载力评价指标体系多种多样,评价方法也日趋丰富。唱彤等[10]基于对水资源承载主体、客体及承载过程的分析,以水资源承载支撑力、压力和调控力描述承载过程,建立了基于承载过程的“水量-水质-水生栖息环境-连通性”四维指标体系。程军蕊等[11]从承载对象角度构建了反映水资源承载、压力和承载度的评价指标体系,体系包括水资源支撑指标、供用水指标和承载力评判指标。王晗等[12]和崔东文等[13]选取水资源、经济社会和生态环境相关指标分别以TOPSIS模型和风力驱动投影寻踪模型对郑州市和文山州近10 a的水资源承载力状况进行了评价。袁艳梅等[14]将灰关联系数应用于模糊评价模型中,结合定性定量分析对江阴市水资源承载力进行了综合评价。王丽等[15]建立了以水资源自然支持力、社会生活水平和经济发展水平3个子系统为主成分的承载驱动回归模型,以评价临海市水资源承载综合能力。张艳明[16]和孟珍珠等[17]均基于人水和谐理论,从健康、发展、协调3方面选取了26个指标,分别对辽宁省和安徽阜阳市的水资源承载力进行了评价。于倩雯等[18]和吴琼[19]分别以模糊物元法和因子分析法对青海省水资源承载力进行了评价。李娟芳等[20]选取了水质、水量、水生态、社会、经济5个方面的28个指标,评价了洛阳市的水资源承载力。任博等[21]基于熵权TOPSIS模型对辽宁省区水资源承载力评价研究,并采用耦合协调模型对系统的耦合协调性进行了分析研究。

综合目前研究成果,水资源承载力的理论研究已经比较完善,评价指标体系及评价方法日趋丰富,不同流域间水资源承载力相互比较以及同一流域水资源系统内部协调性研究较多,但水资源承载效率研究甚少。水资源是集中自然、生态、经济的复杂系统,对水资源的开发利用可以理解为一种庞大的投入产出系统,投入要素中的水资源数量、水资源质量、水域空间形态、水流情势变化与水资源产出(或承载)的人口、GDP、能源、粮食、生物多样性等之间具有复杂的投入产出关系,也存在效率高低问题。本文以珠江水资源公报数据[27]为基础,通过对经济规律、自然规律、生态规律的认识和把握,统筹自然演化、生态服务和社会服务三大功能,围绕水资源载体主体、水资源承载客体以及主客体之间支撑保障途径3个方面,构建了包含32个评价指标的水资源承载力评价指标体系,采用TOPSIS模型、耦合协调模型,对珠江区27个重点流域的水资源承载力排位、水资源系统协调性进行分析研究;并在此基础上,借用生产函数概念提出水资源承载效率模型,对27个重点流域水资源承载效率进行了分类,综合水资源承载力相对排位、水资源系统内部耦合协调程度以及水资源承载效率,对27个重点流域的水资源承载状况进行了研究与评价,以便实现人口经济和生态环境的均衡发展。本分析评价研究结果可作为珠江区及重点流域水资源规划、开发、利用、保护和管理的重要参考,在水资源承载效率研究方面也为水资源承载力研究提供了一个全新的研究领域。

1 研究区域概况

珠江区地处中国东经102°06′～117°18′、北纬3°41′～26°49′,是中国大陆最南端的一个水资源一级区,包括珠江流域、韩江流域、粤东、粤西、桂南沿海诸河和海南岛及南海各岛诸河等水系,行政区域涉及云南、贵州、广西、广东、湖南、江西、福建、海南等八省(自治区)以及香港、澳门特别行政区,总面积57.91万km2。珠江区水系发达、河流众多,集水面积大于1 000 km2的河流约有180条,分属珠江、韩江、粤西、粤东、桂南沿河诸河、海南岛诸河等水系,其中珠江流域最大,韩江流域次之。

同时,以跨省(自治区)重要江河、生态环境脆弱敏感河流、水事矛盾突出河流、水资源开发利用需求强烈河流、现状水资源开发利用程度高河流作为重点,确定了重点流域27个,分别为西江、南盘江、黄泥河、北盘江、六硐河、柳江、都柳江、龙江、郁江、右江、桂江、贺江、北江、武水、东江、深圳河、韩江、汀江、榕江、漠阳江、鉴江、九洲江、南流江、钦江、南渡江、昌化江、万泉河,重点流域总面积49.7万km2,占珠江区总面积的85.8%。

2 数据来源及研究方法

采用的数据主要来源于珠江水资源公报。结合珠江区重点流域水资源自然特点和经济社会发展特征,围绕水资源承载主体、承载客体以及主客体之间支撑保障途径3个方面,构建多指标综合评价指标体系,采用隶属度函数对单指标量化、采用等权模型进行多指标综合,利用TOPSIS模型、耦合协调模型和生产函数模型,对珠江区27个重点流域的水资源承载状况进行分析研究。

2.1 指标体系建立

根据文献[1]、[4],水资源承载系统由3部分构成:承载主体、承载客体及途径。承载主体即水资源的自然要素,具体为水量、水质、水域空间以及水流情势;承载客体即水资源自然要素所能承载的人口、经济、粮食、能源、生态等;途径即承载主体支撑承载客体在发展过程中的能力与效率,主要包括水资源开发能力、节约用水效率、水污染治理水平等。

本文遵循指标体系建立的科学性、代表性、完备性、可操作性等原则,选取32个评价指标(xij,i=1,2,…,27,j=1,2,…,32,i为评价对象,j为评价指标),建立以目标层、准则层及指标层为框架的水资源承载能力评价指标体系,见表1。

表1 珠江区重点流域水资源承载力评价指标体系

32个指标中,正向指标(指标数值越大代表越优)24个、反向指标(指标数值越大代表越差)8个。为避免重点流域在集水面积大小、河流长度、经济规模等指标之间存在的悬殊差异给评价结论造成不客观和难于横向比的实际情况,本次评价指标均采用单位指标和相对指标,其中单位指标14个,相对指标18个,这些指标大多是水资源调查评价中采用的基础评价指标,概念明确、清晰、便于计算。其中,生物多样性为综合性指标,本次采用劣Ⅴ类河流长度占比代替,认为劣Ⅴ类河流占比越高则生物生存条件及多样性越差。

2.2 单指标量化

本文采用隶属度函数量化指标xij(i=1,2,…,27;j=1,2,…,32),量化后大小为[0,1]。正向指标的隶属度(rij)随指标值增大而增大,反向指标的隶属度随指标值增大而减小。计算公式见式(1)、(2)。

对于正向指标:

(1)

对于反向指标:

(2)

2.3 多指标综合

确定各指标相对其准则层的权重,根据各指标的隶属度,按照权重加权计算各准则层指数,即得到代表承载主体的水资源状况指数(SKIi)、代表途径的水资源能力与效率指数(SNIi)、代表承载客体的水资源承载量指数(SZIi),计算公式为:

(3)

(4)

(5)

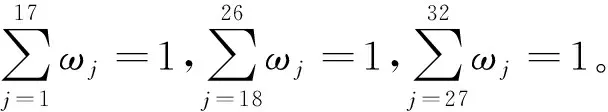
2.4 多准则集成及评价标准划分

确定各准则层相对目标层的权重αj(j=1,2,3),本文采用TOPSIS模型进行多准则集成。TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)评价模型于1981年由Hwang教授提出。该模型属于多目标决策的一种方法,其原理是通过计算评价对象与最优、最劣理想解之间距离,从而对评价对象进行优劣排序。首先,该模型根据各待评对象数据计算出正理想解(最优)与负理想解(最劣);其次,分别计算各待评对象与正、负理想解之间的距离;最后,对所有对象进行排序,从而反映出评价结果的优劣。由于TOPSIS评价模型计算方法简洁,已广泛应用于资源环境评价等领域,计算过程如下[1,21]。

a)正负理想点。准则层中代表主体、客体、途径的相应水资源指数的理想目标划分为正、负理想点,计算方法如下:

(6)

(7)

b)测度距离的计算。正负理想点与水资源指数之间的综合测度距离D1、D2采用欧拉距离定义,其表达式为式(8)、(9)。

(8)

(9)

c)确定贴近度。理想点贴近度Ui可反映水资源承载力水平,其是在各评价指标的综合影响下形成的相对值,理想点贴近度的计算见式(10)。

(10)

式中Ui——贴近正理想点程度的参数,取值区间为[0,1],其值越大则越接近于正理想点,可将其划分为7个评价等级,见表2。

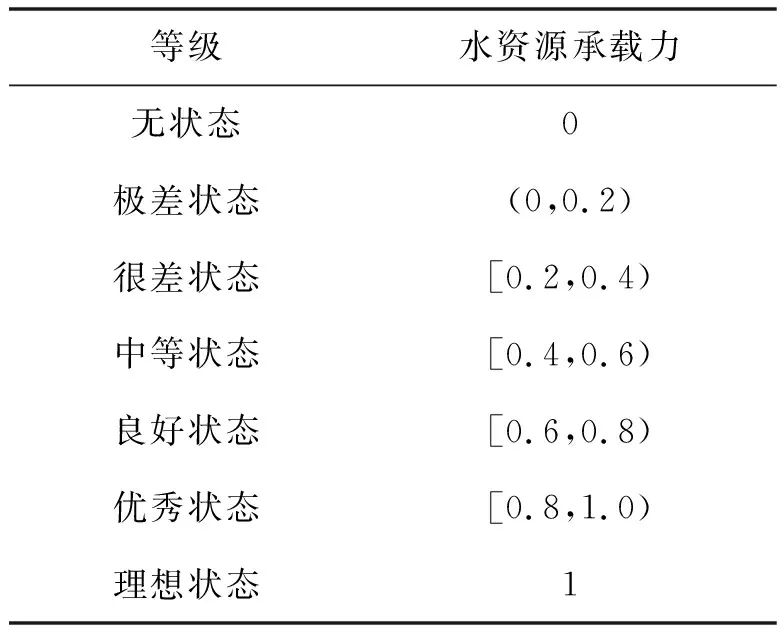
表2 水资源承载力评价等级划分

2.5 耦合协调模型及协调性评价标准

水资源承载力是受多个子系统耦合作用形成的动力系统,分析水资源承载主体、承载客体、途径3个子系统之间相互影响的程度大小,可采用耦合协调度模型[21]。计算见式(11)—(13):

(11)

T=α1×SKI×α2×SNI×α3×SZI

(12)

(13)

式中 SKI、SNI、SZI——水资源承载主体、承载客体、途径系统的水资源指数,具体水资源状况指数(SKIi)、水资源能力与效率指数(SNIi)、水资源承载量指数(SZIi);C——耦合度;T——发展度;D——耦合协调度。

根据文献[21]相关研究,耦合协调度划分见表3。

表3 水资源系统协调发展水平度量标准

2.6 权重确定

权重确定的方法有多种,本文采用指标等权处理。等权处理简单而且不会特别强调某个指标也不会弱化某个指标,可以兼顾每个指标在综合评价中地位与作用,避免了因某一个指标对计算结果的过度集中而失去综合评价意义。指标层指标权重分别为:ωj=1/17(j=1,…,17)、ωj=1/9(j=18,…,26)、ωj=1/8(j=27,…,32);准则层指数αj=1/3(j=1,2,3)。

经等权TOPSIS模型及耦合协调度模型计算,27个重点流域2010、2016年水资源承载力及其代表承载主体、承载客体、途径的水资源状况指数、水资源能力与效率指数、水资源承载量指数见表4、图1,2010、2016年水资源系统耦合协调度及协调水平见表5、图2。

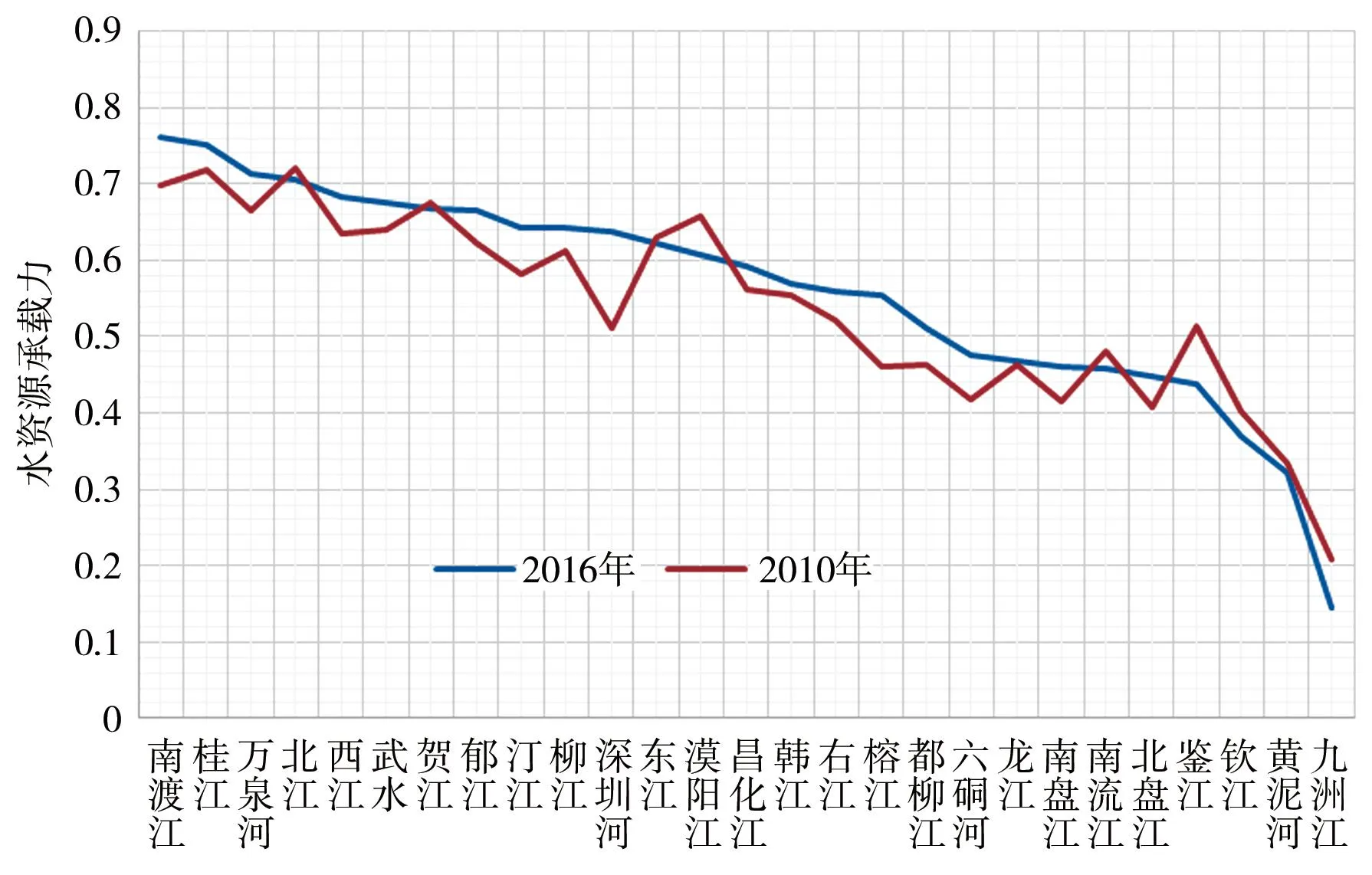
图1 重点流域水资源承载力分布

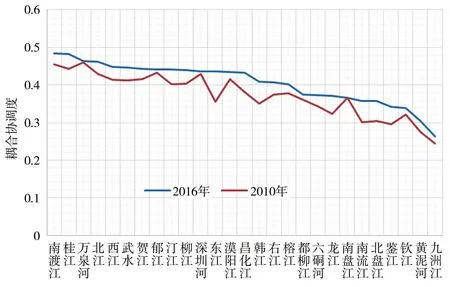
图2 重点流域水资源系统耦合协调度分布

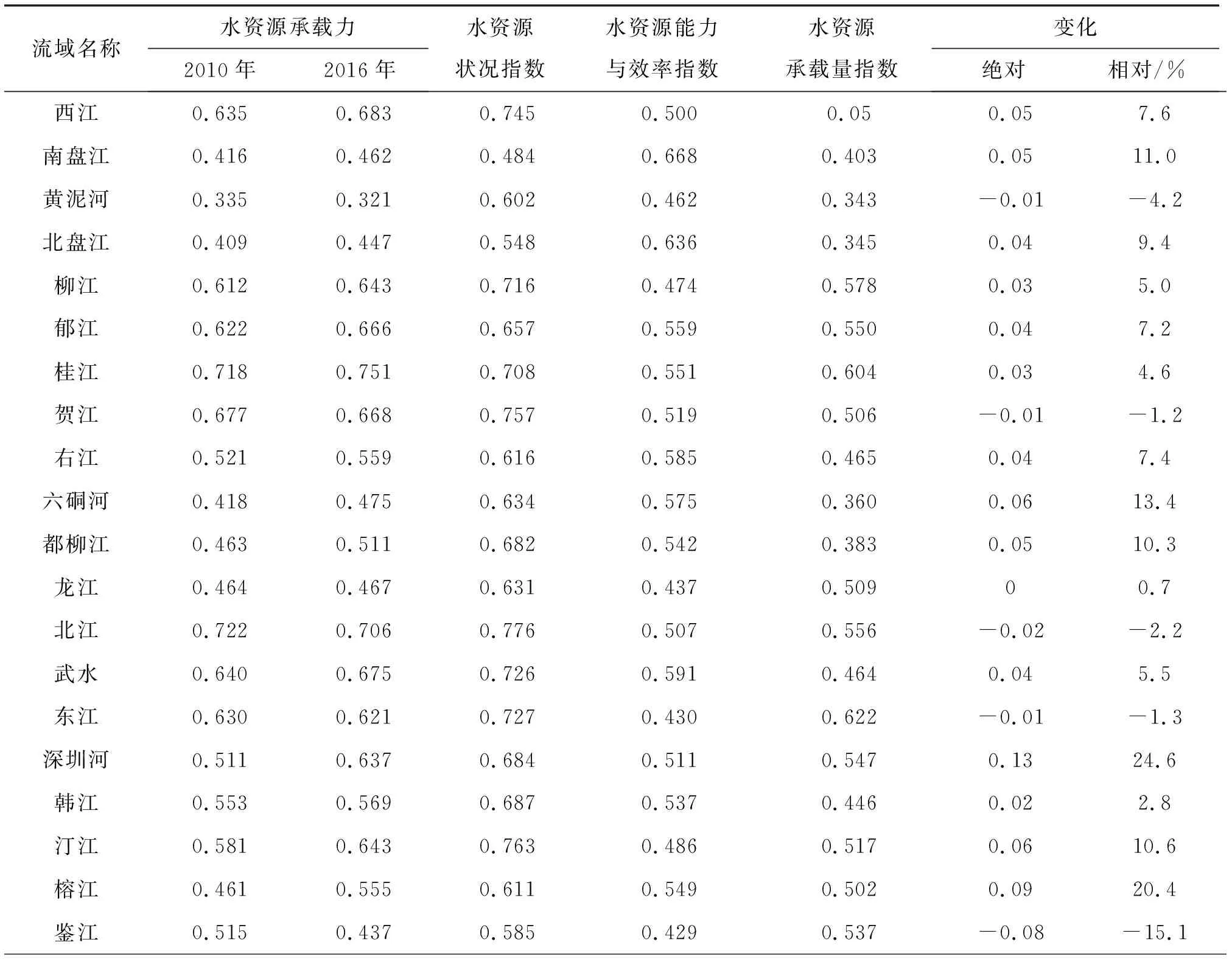
表4 重点流域水资源承载力计算

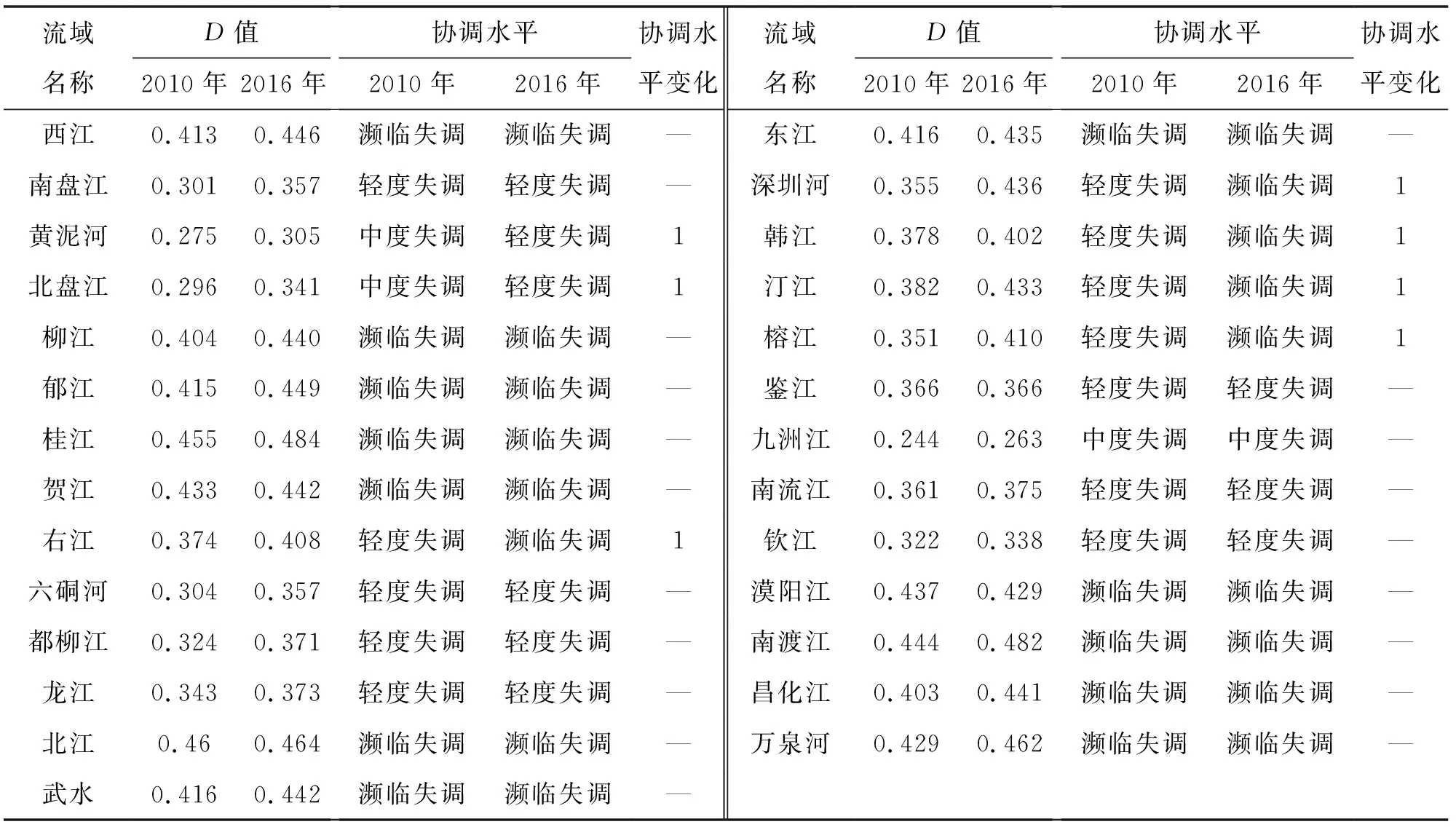
表5 重点流域水资源系统耦合协调度及协调水平

2.7 生产函数模型

“生产”在经济学中是一个具有普遍意义的概念,其不仅仅意味着制造一台机床或是纺织一匹布,它还包含了其他各种各样的经济活动,如经营一家商店或证券公司、出租车的客运服务、为他人打官司、剧团的演出、为病人看病等等。表示这种经济生产过程中投入与产出的数量关系即为生产函数,通用的生产函数表达式为:Q=f(L,K),其中Q为产出量,L为投入量,K为科技水平。一般情况下,在相同的科技水平条件下,投入量越大则产出量越大;在投入量一定的情况下,科技水平越高则产出量越高。

水资源系统中的承载主体、承载客体以及主客体支撑保障途径也可以理解为一种水资源投入产出关系,其具体的数量关系即为水资源承载力生产函数。其中,水资源承载主体即为投入量,具体为投入的水资源数量、水资源质量、水域空间形态、水流情势变化,水资源承载客体即为产出量,具体为产出或者承载的人口、GDP、能源、粮食、生物多样性等。主客体支撑保障途径即为水资源生产过程中的科技水平,具体为水资源开发能力、节约用水效率、水污染治理水平等。与经济学意义上的生产函数不同,水资源承载力投入与产出的数量关系更为复杂。

本文利用建立的水资源承载力评价指标体系以及准则层水资源状况指数SKI、水资源能力与效率指数SNI、水资源承载量指数SZI,建立水资源承载效率函数:SZI=f(SKI,SNI),重点流域 2010—2016 年平均水资源承载效率函数关系见图 3。

3 结果分析

3.1 水资源承载力排位

重点流域2016年水资源承载力为0.762～0.146,平均值为0.561,其中良好状态流域13个,占比为48.1%;中等状态的流域11个,占比为40.7%;很差状态流域2个,占比为7.4%;极差流域1个,占比为3.7%。重点流域总体上以良好状态河流为主。南渡江、桂江、万泉河、北江流域水资源承载力排位相对居前,九洲江、黄泥河、钦江、鉴江流域水资源承载力排位相对居后。九洲江流域位于桂南沿海,源短流急,水资源丰枯变化大,水资源与经济社会发展之间矛盾突出,人均水资源量1 912 m3、为重点流域平均水平的45.0%,人均GDP3.0万元、为重点流域平均水平的74.1%,水资源开发利用率高达46.1%,全年期符合或优于地表水Ⅲ类水质标准(优良)的河流长度占比为76.0%、水库蓄水量占比为60.0%,水库轻度富营养占比为60.0%,是唯一一个水资源承载力处于极差状态的流域。

对比2010、2016年各重点流域水资源承载力,水资源承载力提高的流域18个、占比为66.7%,降低的流域9个、占比为33.3%,总体上水资源承载力以提高为主,说明珠江区重点流域水资源承载状态逐步向理想状态发展。水资源承载力降低的流域有黄泥河、贺江、北江、东江、鉴江、九洲江、南流江、钦江、漠阳江,其中南流江、东江、鉴江、北江、漠阳江流域水资源承载力下降主要是因为水体水质变差导致水资源状况指数下降进而影响承载力排位,其2010—2016年全年期符合或优于地表水Ⅲ类水质标准(优良)的河流长度占比分别下降了42.4%、12.5%、12.5%、10.4%、6.0%;黄泥河、贺江流域水资源承载力下降主要是水资源承载客体规模不足,经济社会发展相对落后所致;九洲江、钦江流域水资源承载力下降主要是水资源丰枯变化大、水资源利用条件差,而水资源利用效率、治理与保护水平跟不上经济社会发展水平所致。

2010—2016年重点流域水资源承载等级无变化的流域24个,变化的流域3个,分别为:汀江、深圳河水资源承载等级由中等提高至良好,钦江水资源承载等级由中等降至很差,九洲江水资源承载等级由很差降至极差,九洲江流域人水矛盾短期内尚未彻底扭转。

3.2 水资源系统协调性

重点流域2016年水资源耦合协调度为0.484～0.263,平均值为0.406,其中濒临失调流域17个,占比为63.0%;轻度失调流域9个,占比为33.3%;中度失调流域1个,占比为3.7%;重点流域总体上以濒临失调为主,无协调级别的流域,这符合珠江区水资源时空分布不均的自然特点以及地区之间经济社会发展水平差异较大、水资源开发治理与保护水平不一的经济社会发展阶段。鉴江、九洲江、南流江、钦江等东部及沿海地区经济社会发展水平相对较高,但河道外用水量及废污水排放量大,水环境质量面临较大的承载压力;南盘江、黄泥河、北盘江、六硐河、都柳江、龙江等西部地区经济社会发展水平落后,水环境质量普遍较高,但水资源承载客体规模相对较小。

对比2010、2016年各重点流域水资源耦合协调度及协调水平,协调水平未发生变化的流域20个,占比为74.1%,协调水平逐步提高的流域7个,占比为25.9%,其中深圳河、韩江、汀江、榕江、右江流域协调水平由轻度失调调整为濒临失调,黄泥河、北盘江流域协调水平由中度失调调整为轻度失调。九洲江流域水资源耦合协调度由2010年的0.244提高至2016的0.263,仍然是流域唯一一个水资源中度失调河流。

3.3 水资源承载效率

根据图3,可将27个重点流域水资源承载效率分为3类。①低效率曲线型(Ⅰ型):相应流域为漠阳江、鉴江、昌化江、九洲江等4个,水资源承载效率曲线为SZI=0.96×f(SKI,SNI)-0.02(R2=0.97)。在当前水资源状况条件和能力与效率水平下,相应流域单位水资源投入变化量可以新增0.96个单位的承载规模。②中效率曲线型(Ⅱ型):相应流域为东江、柳江、桂江、万泉河、南渡江、深圳河、郁江、龙江、右江、钦江、榕江、南流江等12个,水资源承载效率曲线为SZI=1.00×f(SKI,SNI)-0.15(R2=0.81),在当前水资源状况条件和能力与效率水平下,相应流域单位水资源投入变化量可以新增1.00个单位的承载规模。③高效率曲线型(Ⅲ型):相应流域为北江、汀江、贺江、西江、武水、韩江、都柳江、六硐河、黄泥河、北盘江、南盘江等11个,水资源承载效率曲线为SZI=1.41×f(SKI,SNI)-0.57(R2=0.92);在当前水资源状况条件和水资源能力与效率水平下,相应流域单位水资源投入变化量可以新增1.41个单位的承载规模。

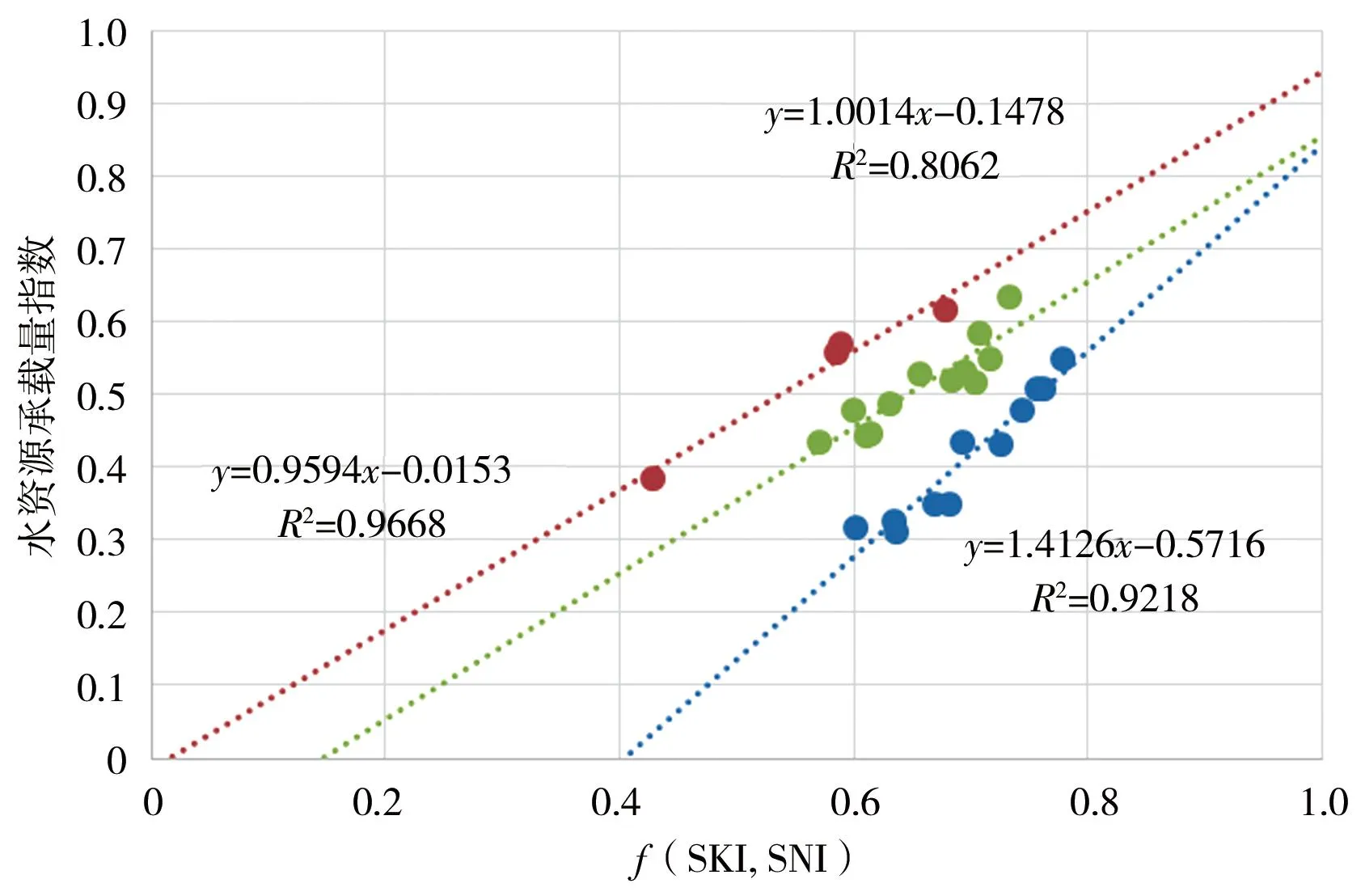
图3 重点流域2010—2016年水资源承载效率函数

对各重点流域做横向比较,当水资源投入量一定情况下,Ⅰ型流域水资源承载产出量大于Ⅱ型流域水资源承载产出量,Ⅱ型流域水资源承载产出量大于Ⅲ型流域水资源承载产出量。据此,Ⅰ型流域为低效率、高产出,属于强承载;Ⅱ型流域为中效率、中产出,属于中承载;Ⅲ型流域为高效率、低产出,属于低承载。

3.4 水资源承载状况

综合水资源承载力排位、耦合协调程度以及承载效率分析成果,水资源承载力排位(WRCC)与耦合协调程度之间具有高度的线性相关关系,曲线为:WRCC=2.54×D-0.47(R2=0.97),说明水资源系统内部要素之间越协调水资源承载力越高,反之而越低;而水资源承载力排位、耦合协调程度与承载效率之间无明显的相关性。

综合水资源承载力排位、系统协调性以及承载效率,可以将27个流域综合为5组:第一组为九洲江、鉴江、钦江,其水资源承载力排位低、系统耦合协调性差、水资源承载效率为Ⅱ～Ⅰ型,综合水资源承载状况不佳;第五组为北江、西江、武水、贺江、汀江,其水资源承载力排位高、系统耦合协调性较好、水资源承载效率为Ⅲ型,综合水资源承载状况相对较佳;第二组为昌化江、龙江、南流江、黄泥河;第三组为漠阳江、右江、榕江、都柳江、六硐河、南盘江、北盘江,第四组为南渡江、桂江、万泉河、郁江、柳江、深圳河、东江、韩江,其综合水资源承载状况介于第一组至第五组之间。

4 结语

本文围绕水资源承载主体、承载客体、途径3个维度,构建了水资源承载力评价指标体系,采用TOPSIS模型、耦合协调模型以及生产函数模型,对珠江区27个重点流域水资源承载状况进行了分析研究。

结果表明:南渡江、桂江、万泉河、北江流域水资源承载力排位居前,九洲江、黄泥河、钦江、鉴江流域水资源承载力排位居后;重点流域水资源系统内部要素之间以濒临失调为主,濒临失调流域17个、轻度失调流域9个、中度失调流域1个;重点流域水资源承载效率曲线呈低、中、高3种类型,低效率型流域4个、中效率型流域12个、高效率型流域11个;综合水资源承载力排位、耦合协调程度以及承载效率,九洲江、鉴江、钦江流域水资源承载状况不佳,北江、西江、武水、贺江、汀江流域水资源承载状况处于最佳状态。

采用隶属度函数法量化评价指标并等权计算了水资源指数,并据此计算了水资源承载力、耦合协调系数、承载效率函数。承载效率函数为本次研究首次提出,为水资源承载力研究提供一个新领域。