不同模态分解方法结合LSTM模型对日径流预报的影响

谭永杰,王现勋*,段茗续,刘亚茹,姚华明,2,3

(1.长江大学资源与环境学院 油气地球化学与环境湖北省重点实验室,湖北 武汉 430100;2.中国长江电力股份有限公司,湖北 宜昌 443000;3.智慧长江与水电科学湖北省重点实验室,湖北 宜昌 443000)

精准可靠的径流预报是防洪减灾、水资源的配置与管理、电力生产等流域管理和调度决策的关键依据,也是全球水文水资源领域研究的热点[1]。径流过程通常受降水、蒸发、地形、土地利用及大尺度气候异常因子等诸多因素的影响,本质上是高度动态的,甚至是混沌的,同时也是非线性和非平稳的[2]。近年来,受气候变化和人类活动的影响,许多流域的水资源状况发生了巨大的改变,径流的一致性因此改变的愈加明显,精准捕捉日径流时间序列的动态过程变得更加困难[3]。为了准确地预测未来时段的径流,国内外水文预报研究者提出了多种预报模型以及预报方法。在这些水文预报模型方法中大致可以分为3个类型。第一种类型是基于统计学原理的水文预报模型,该模型主要是通过对历史水文数据进行分析和拟合,来预测未来水文过程的变化趋势。常用的统计学方法包括回归分析[4]、时间序列分析[5]、聚类分析[6]等。这种模型具有简单易用的优点,适用于数据量较少的情况,但存在着较大的误差和不确定性。第二种类型是基于物理学原理的水文预报模型,该模型主要是基于水文过程的物理规律,通过建立数学公式来描述水文的变化过程。常用的模型包括新安江模型[7-8]、水箱模型[9]、HBV模型[10]等。这种模型具有较高的准确性和可靠性,但需要大量的数据和对水文过程的深入理解。第三种类型是基于人工神经网络的水文预报模型,该模型主要是通过模拟人脑神经元的工作原理,来建立水文过程的非线性模型。常用的神经网络模型包括(Back Propagation,BP)反向传播神经网络[11]、(Extreme Learning Machines,ELM) 极限学习机[12]、(Support Vector Networks,SVM)支持向量机[13]、(Long Short Term Memory,LSTM)长短期记忆神经网络[14]等。由于深度学习算法能更好的模拟非线性、非平稳的时间序列,可以更加准确地进行径流预报,逐渐成为近年来新的研究热点。

随着近几年学者的深入研究,不少学者发现径流时间序列是含有多种频率和趋势成分的非线性非平稳时间序列,其非平稳性和非线性增加了预报的预测难度[15-17]。不少研究表明将时域分析的数据预处理方法与神经网络模型组合可以提高径流预报的精度。李福兴等[18]采用经验模态分解算法(Empirical Mode Decomposition,EMD)提取径流序列中具有物理含义的信号并得到不同时间尺度的多个固有模态函数(Intrinsic Mode Functions,IMF),在利用(Autoregressive Integrated Moving Average,ARIMA)自回归移动平均模型与(Generalized Regression Neural Network,GRNN)广义回归神经网络分别对不同时间尺度的IMF进行模拟,分析径流未来变化趋势,预测结果表明,其提出结合EMD模态分解算法的组合预测模型能取得较好的预测效果;王秀杰等[19]利用时变滤波器的经验模态分解(Time-Varying-Filter,Empirical Mode Decomposition,TVF-EMD)分解原始径流序列,再利用(Grey Relation Analysis,Light Gradient Boosting Machine,GRA-LightGBM)组合模型进行预测,结果表明结合模态分解算法的组合预测模型较其他模型拥有更高的精度。刘扬等[20]提出一种改进的集合经验模态分解算法(EEMD)将径流信号分解为若干模态分量,在将各分量分别输入门控循环单元(Gate Recurrent Unit,GRU)神经网络进行预测,预测结果表明,该组合模型拥有更高的预测精度,可进一步减少防洪区的经济损失。但上述所描述的模态分解算法仍存在一定缺陷,EMD受独特的分解原理限制,基于EMD的分解理论存在的模态混叠现象和端点效应等问题,且只能被削弱而难以根除;EEMD模型在添加噪音时使用了随机数,将导致每次分解结果都存在微弱偏差,结果难以完全复现。而基于自适应噪声的完整集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN)[21]方法是一种建立在EMD分解和EEMD分解基础上的自适应白噪声分解方法,在分解过程中的每一阶段都添加有限次的自适应高斯白噪声,不仅克服了EMD分解模态混叠问题,还解决了EEMD方法在较少的实验平均次数下导致重构误差较大以及计算效率低的缺点。胡斯曼[22]将CEEMDAN模态分解算法运用于月径流、年径流的预测中,且取得了不错的预测效果,但在更具非平稳性、非线性的日径流时间序列的运用却少有涉及,在应对更加复杂的日径流序列中,还有待进一步探究。

针对上述问题,结合不同的时域分解算法和LSTM模型,构建基于经验模态分解(EMD)算法、集合经验模态分解(EEMD)算法、完整经验模态分解(CEEMDAN)算法并利用(Grid Search,GS)网格搜索参数寻优算法[23]对LSTM模型的超参数进行寻优的组合预测模型,对日径流进行预报。以宜昌水文站为研究区域,其日径流时间序列为研究对象,比较不同模态分解算法构成的组合预测模型的预测精度,结果表明结合CEEMDAN的GS-LSTM组合预测模型拥有更高的预测精度。

1 研究方法

1.1 经验模态分解(EMD)和集合经验模态分解(EEMD)

在处理非平稳和非线性时间序列数据方面,HUANG等[24]于1998年提出的EMD在处理信号时,将会产生一组固有模态函数,消除了寄生谐波来表示非线性和非平稳信号的需要。众多文献表明其在处理如径流[25]、风速[26]非线性时序数据时具有明显的优势。EMD的技术步骤如下。

步骤一找到原始径流时间序列S(t)的所有局部最大值和局部最小值,然后用三次样条曲线拟合S(t)的上包络线U(t)和下包络线L(t),并求出上下包络线的均值系列M(t),见式(1):

(1)

步骤二使用原始时间序列S(t)减去均值序列M(t)得到一个新的时间序列H(t),见式(2):

H(t)=S(t)-M(t)

(2)

步骤三如果M(t)和H(t)满足终止标准,可以得到第一个IMF为c1(t)=M(t)和第一个残差R为r1(t)=H(t),其终止标准为①M(t)接近于0;②H(t)中局部最小极值点和零交叉点的数量必须相同或最多相差一个。

步骤四如果不满足终止标准,对H(t)重复步骤一—三,直到得到c1(t)和r1(t)。

步骤五对r1(t)重复上述步骤一—四,直到得到所有的IMF和残差。因此,原始时间序列S(t)将按照式(3)被分解。

(3)

式中ci(t)——第i个IMF;rk(t)——第k个残差项。

尽管EMD技术在实际应用中取得了不错的效果,但其分解得到的IMF存在模态混叠现象,给IMF的重构带来一定的困扰。Wu等[27]于2009年提出了一种名为EEMD的噪声辅助数据分析方法,其最大优点在于其能够以自适应方式提取信号的各分量及变化趋势,同时显著地减少了经验模态分解(EMD)方法中存在的模态混叠现象,克服了小波变换容易造成很多虚假的没有原有物理意义的谐波的缺点[28]。其通过在分解的过程中多次引入均匀分布的白噪声,将信号本身的噪声通过多次人为添加的噪声掩盖过去,从而得到更加精准的上下包络线。同时对分解结果进行平均处理,平均处理次数越多,噪声给分解带来的影响就越小。EEMD的技术步骤如下:①在原时间序列中加入高斯白噪声,然后得到一个新的时间序列;②分解新的时间序列以获得每个IMF成分;③连续重复①和②,但每次都使用不同的高斯白噪声;④以分解的相应IMF的合计平均值作为最终结果。

1.2 完整集合经验模态分解(CEEMDAN)

基于自适应噪声的完整集合经验模态分解(CEEMDAN)方法是一种建立在EMD分解和EEMD分解基础上的自适应白噪声分解方法,在分解过程中的每一阶段都添加有限次的自适应高斯白噪声,不仅克服了EMD分解的模态混叠问题,还克服了EEMD方法在较少的实验平均次数下导致重构误差较大以及计算效率低的缺点。

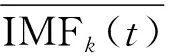
步骤一通过添加一个白噪声wi(t)(i=1,2,……,n),信噪比为ε0到原始日径流时间序列S(t),得到的S(t)被用来进行一次分解,见式(4)。其中t代表不同的时间点,i代表第i次加入的白噪声,n代表加入白噪声的总数。

Si(t)=S(t)+ε0ωi(t)

(4)

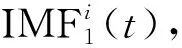
(5)

(6)

步骤三自适应噪声项是通过EMD获得的第一个IMF,加上白噪声ωi(t)且信噪比为ε1然后加入自适应噪声项得到第一个残差R1(t),并得到一个新的时间序列。随即利用式(7)分解得到CEEMDAN的第二个IMF,第二个残差R2(t)根据式(8)计算得到。

(7)

(8)

步骤四重复步骤三,加入新的自适应噪声得到新的时间序列与残差项,然后分解得到CEEMDAN的第K个IMF,其中ωi(t),(i=1,2,…n),εk,(k=2,3,…K),计算步骤见式(9)、(10)。

EMDk-1(ωi(t)))

(9)

(10)

步骤五最后,CEEMDAN算法的残差项不能继续分解,因为不会超过2个极值点,因此最终残差项R(t)是一个独特的趋势项。获得的完整IMF和R(t)与原始日径流时间序列见式(11)。

(11)

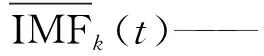
1.3 LSTM模型

LSTM[29]网络是循环神经网络(Recurrent Neural Network,RNN)的一种改进网络,在时间反馈机制基本不变的情况下,引入了记忆单元(memory cell)和门(gate)的机制,来实现对信息流的存储和控制。该机制保障了信息在其特殊的神经元结构中实现长期性的筛选与保留,从而有效避免横向深度带来的信息丢失问题。此外,记忆单元的门控机制也使得梯度下降时,梯度的衰减得到缓解,有效缓解了模型训练时的梯度消失与梯度爆炸的问题。

图1所示,LSTM单元中有3种类型的门控,分别为输入门、遗忘门和输出门。图中分别使用i、f和o来表示输入、遗忘和输出门,⊙代表对应元素相乘,W和b表示网络的权重矩阵和偏置向量。

LSTM的计算过程大致可以用式(12)—(16)表示,在时间步为t时,LSTM的隐藏层的输入和输出向量分别用xt和ht表示,记忆单元用ct表示。输入门用于控制网络当前输入数据xt流入记忆单元的多少,即ct可以保存多少有效信息,见式(12):

it=σ(Wxixt+Whiht-1+bi)

(12)

遗忘门是LSTM单元的核心组成部分,其可以保留部分信息并遗忘部分信息。遗忘门控制自连接单元,可以决定历史信息中的哪些部分会被丢弃,即上一时刻记忆单元ct-1中的信息对当前记忆单元ct的影响见式(13)、(14)。

ft=σ(Wxfxt+Whfht-1+bf)

(13)

ct=ft⊙ct-1+it⊙tanh(Wxcxt+Whcht-1+bc)

(14)

输出门控制记忆单元ct对当前输出值ht的影响,即记忆单元中的部分信息会在时间步t输出。输出门的表达见式(15),LSTM单元在t时刻的输出ht可以通过式(16)得到。

ot=σ(Wxoxt+Whoht-1+bo)

(15)

ht=ot⊙tanh(ct)

(16)

2 实例分析

2.1 研究区域及数据

本文以长江流域中的宜昌水文站为研究对象,宜昌水文站位于三峡工程下游距三峡水利工程约44 km处,地处长江上游与中游的交界处,被视为干流上中游的咽喉。已知宜昌水文站控制流域面积占到整个流域面积的55%,该站所测径流多年平均径流量为4 131亿m3,其中汛期平均流量为3 412亿m3,占全年径流量的79%左右[30],研究区域见图2。

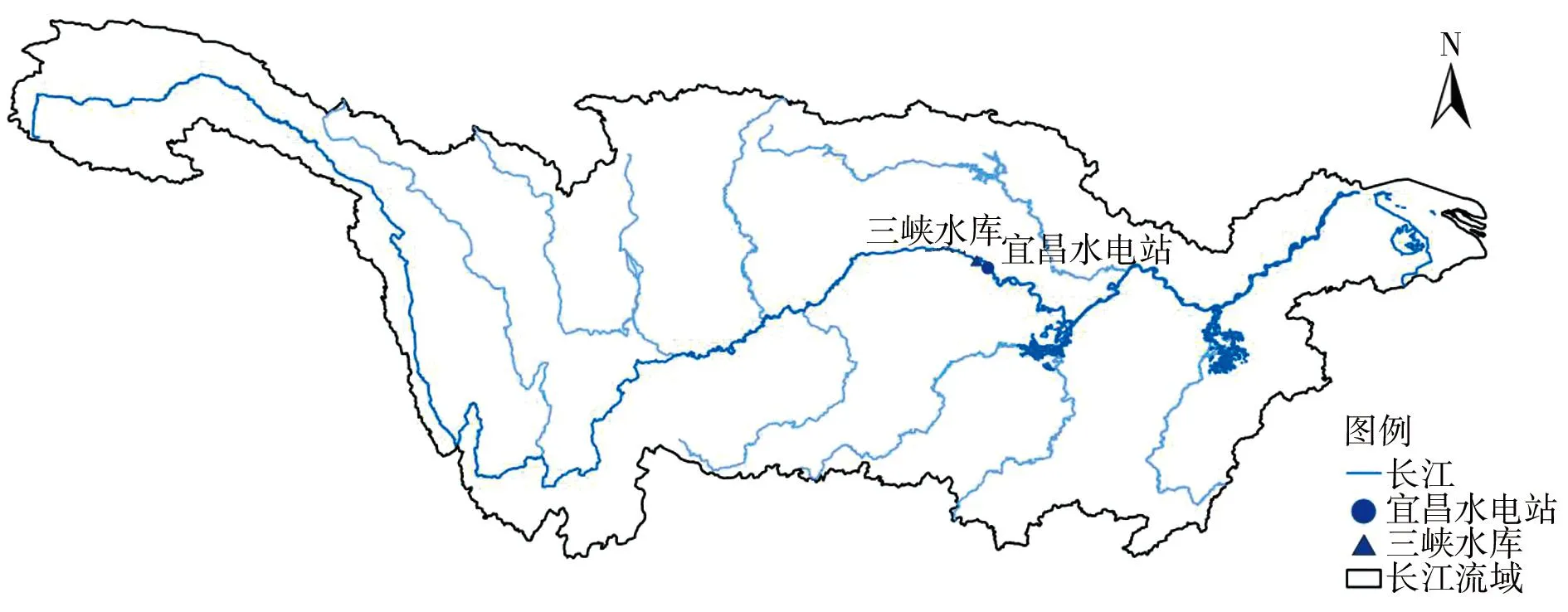
图2 宜昌水文站地理位置示意

本文采用长江流域宜昌水文站1952年1月1日至2020年12月31日实测(日)径流资料进行分析,其径流数据见图3。

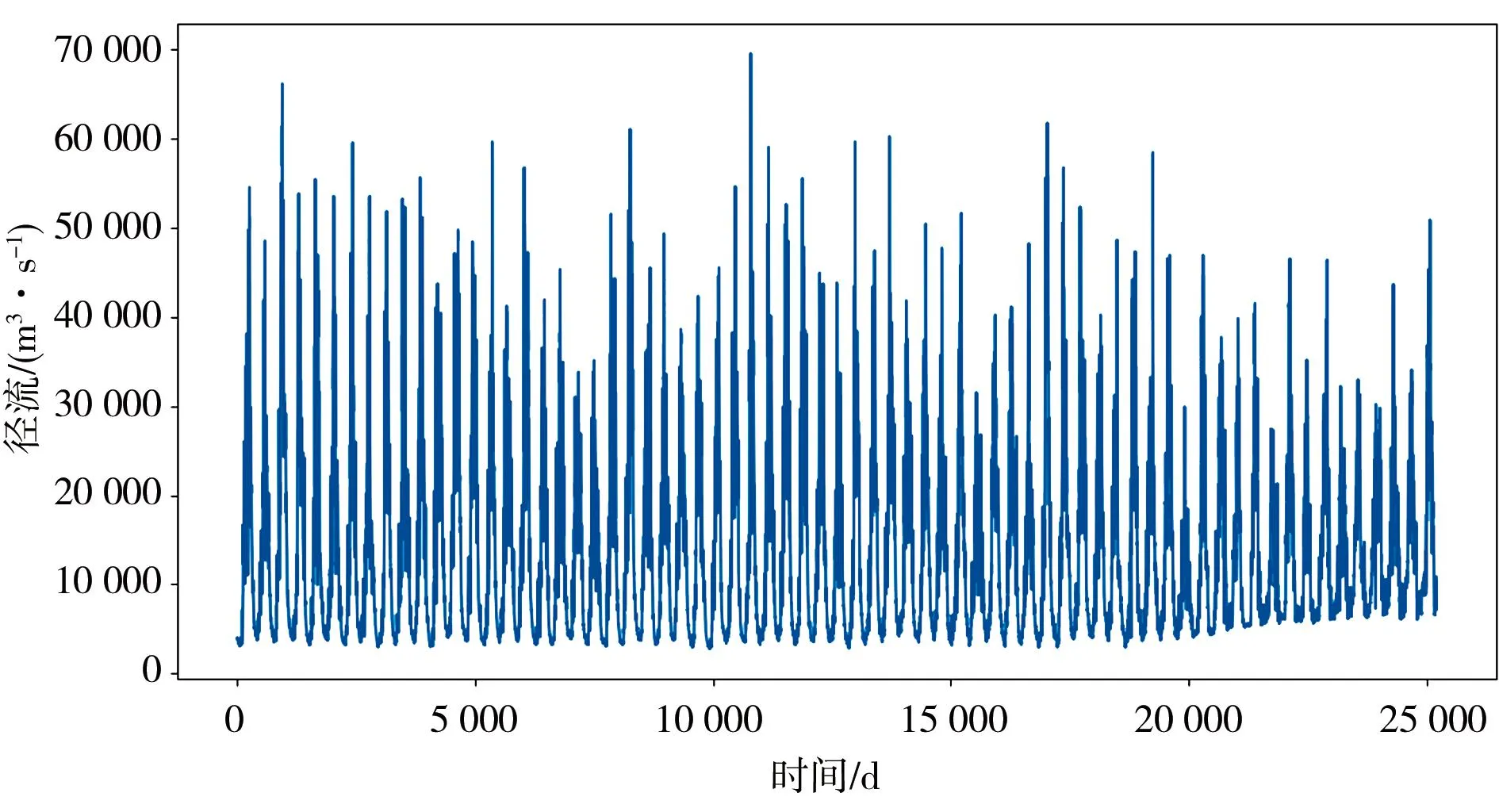
图3 径流数据

2.2 评估指标

在评估模型的性能时,均方根误差(Root Mean Square Error,RMSE)是预测值与实际值之间差异的平方的平均值的平方根;平均绝对误差(Mean Absolute Error,MAE)是预测值与实际值之间差异的绝对值的平均值;平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)是预测值与实际值之间差异的绝对值与实际值之间的比率的平均值。本文采用RMSE、MAE和MAPE统计指标来进行评价[31],见式(17)—(19):

(17)

(18)

(19)

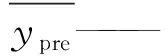
2.3 模态分解

利用上述EMD、EEMD、CEEMDAN 3种模态分解算法对宜昌水文站1952年1月1日至2020年12月31日的日径流时间序列进行分解,使用EMD将原始序列自适应的分解为若干个子模态,结果见图4;使用EEMD、CEEMDAN对径流时间序列进行分解,分解内容见图5、6。

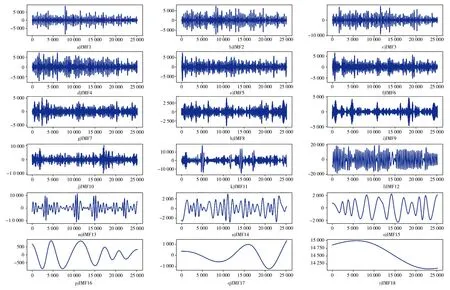
图4 EMD模态分解

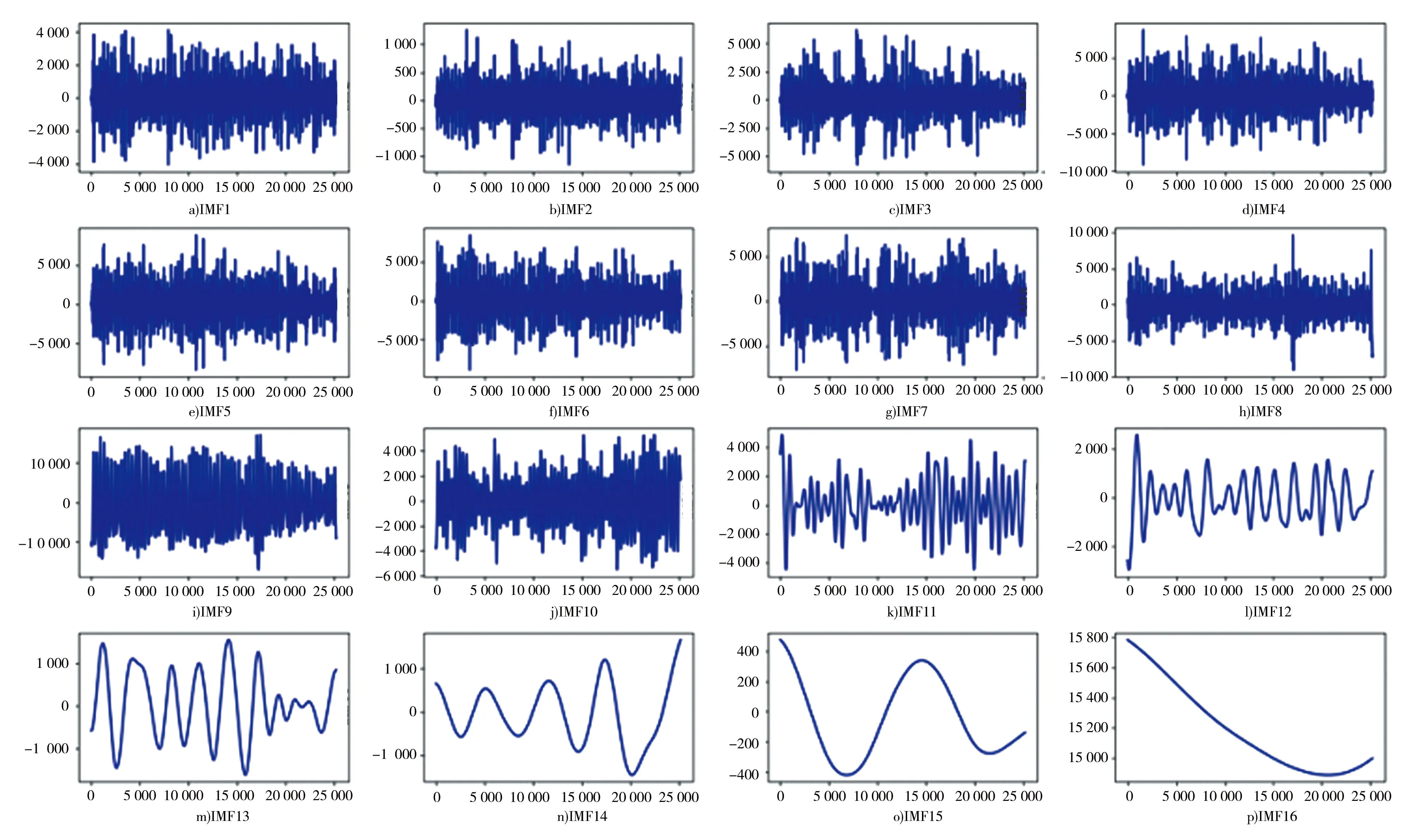
图5 EEMD模态分解

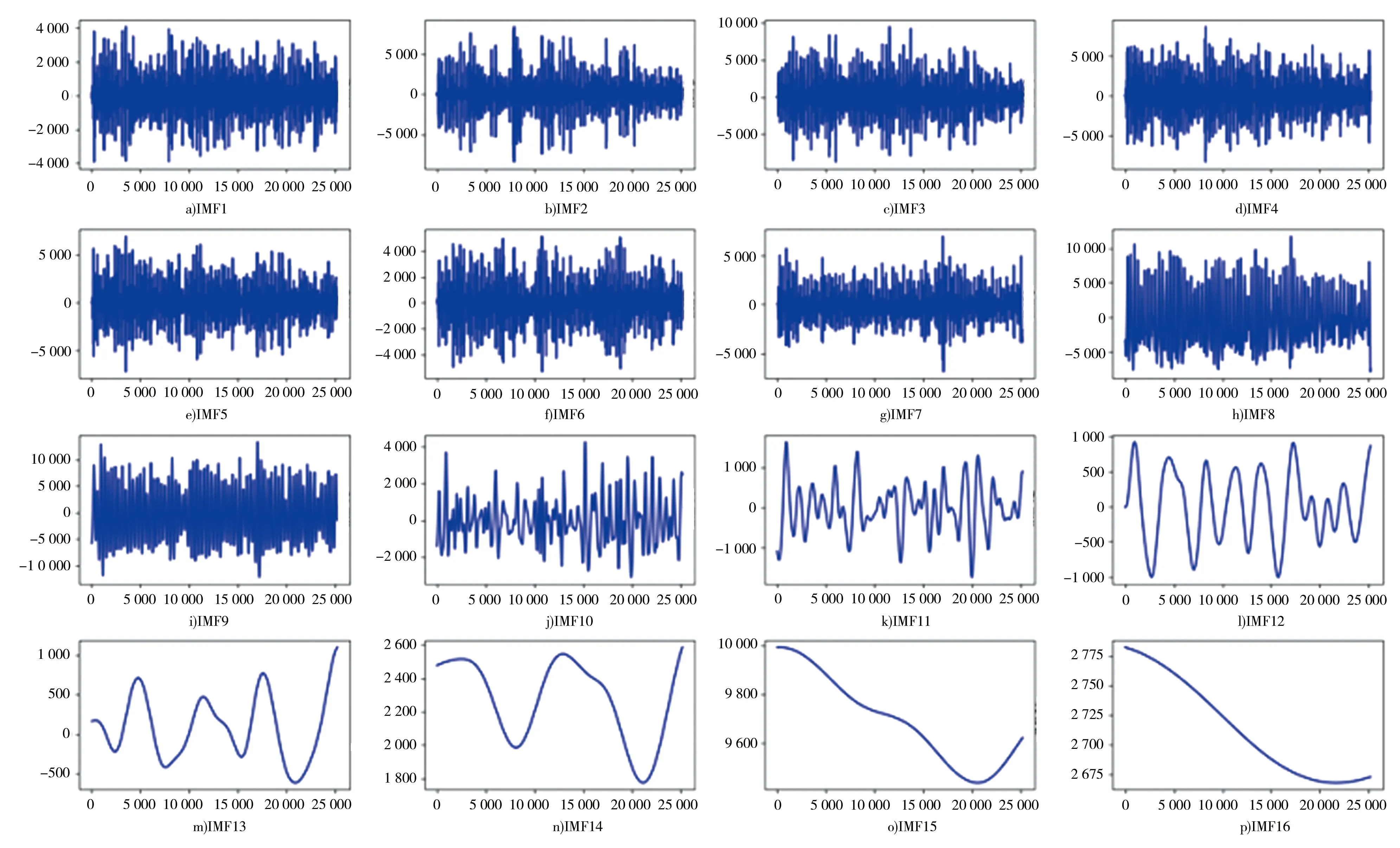
图6 CEEMDAN模态分解

2.4 预报结果与分析

利用上述模态分解算法对宜昌水文站1952年1月1日至2020年12月31日的日径流数据进行分解,按照1952年1月1日至1999年10月22日为训练数据,1999年10月23日至2020年12月31日为测试集,并将分解后的模态分别输入LSTM模型进行预测,并将各模态的预测结果进行加和得到最终的预测值,本算例直接选取10 d的历史径流数据预测下1 d的径流,考虑到预见期过短,无法提供太多参考价值,因此采用滚动预报的方式去增长日径流预见期,并利用网格搜索参数寻优算法选择的超参数设置见表1,其预测流程见图7。

表1 LSTM超参数及取值

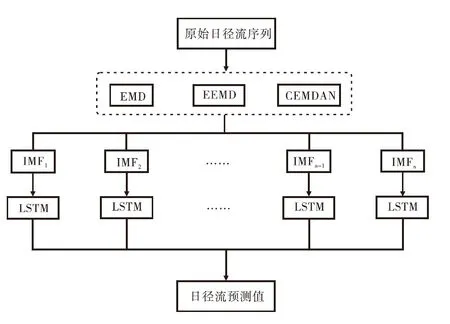
图7 预测流程

为验证模型预测性能,对以下4种模型的结果分别进行讨论,以下4种模型均按照上述网格搜索算法寻优的超参数进行设置,4种模型的评价指标结果见表2、图8。

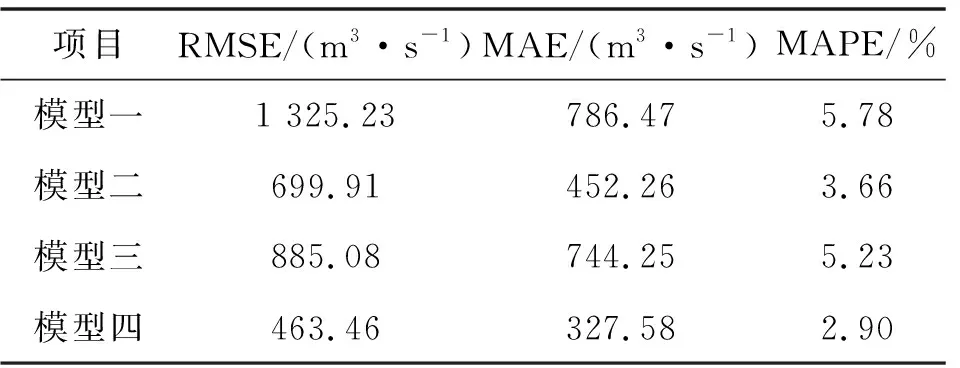
表2 4种模型评价指标比较

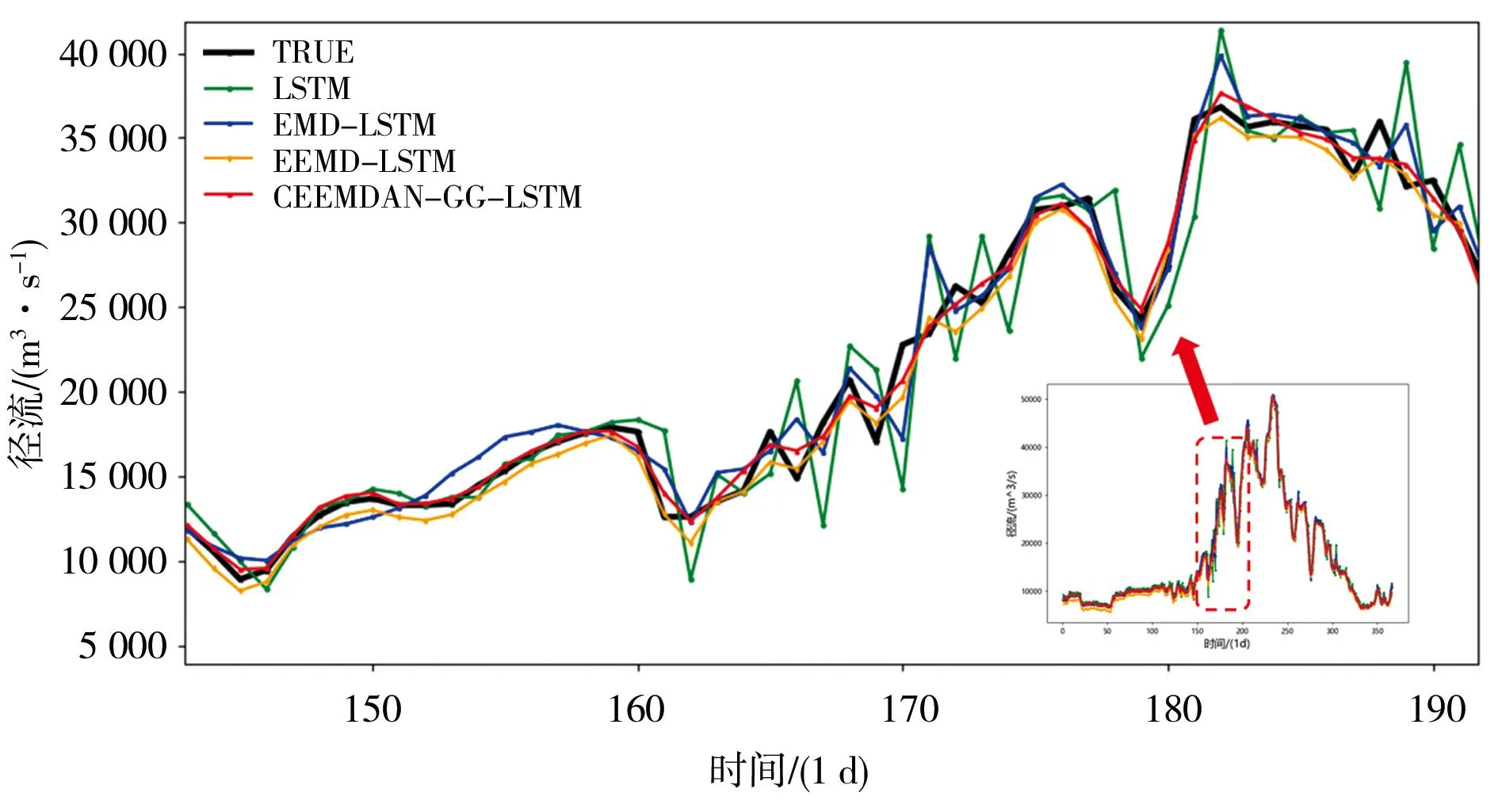
图8 预测结果对比

模型一(GS-LSTM):将原始日径流时间序列直接输入LSTM模型进行预测。

模型二(EMD-GS-LSTM):运用EMD模态分解算法先将原始日径流时间序列进行分解,然后分别输入进LSTM模型进行预测,最终将各个预测值进行加和得到径流预测值。

模型三(EEMD-GS-LSTM):使用EEMD模态分解算法先将原始日径流时间序列进行分解,然后分别输入进LSTM模型进行预测,最终将各个预测值进行加和得到径流预测值。

模型四(CEEMDAN-GS-LSTM):利用CEEMDAN模态分解算法先将原始日径流时间序列进行分解,然后分别输入进LSTM模型进行预测,最终将各个预测值进行加和得到径流预测值。

从表2、图8可以看出,RMSE在463.46～1 325.23,MAE在327.58～786.47,MAPE在2.90%～5.78%,均处于较低水平,LSTM模型能较好地预测日径流的总体趋势,此外可以看出模型四(CEEMDAN-LSTM)的预测精度优于其他4个模型的精度,说明其在日径流预报中拥有更好的表现。

a)将模型一(GS-LSTM)的预测结果与其他模型预测结果对比,可以看出将模态分解算法加入到日径流的预测,可以提高模型的预测精度,与模型四相比,其RMSE、MAE和MAPE分别降低了65.02%、58.35%与2.88%,有效降低了径流时间序列的非平稳性与波动性,使得径流序列更易被LSTM模型捕捉,从而取得更好的预报效果。

b)将模型二(EMD-GS-LSTM)与模型三(EEMD-GS-LSTM)的预测结果进行比较,模型二的预测结果略微优于模型三,其RMSE、MAE和MAPE分别降低了20.91%、39.23%与1.57%。在使用EEMD算法对径流时间序列进行分解时,由于随机噪声的加入,导致在模态分解时存在微弱的偏差,进而影响到预测结果,这表明传统的模态分解算法在进行时域分解时仍存在一定的缺陷,若对模态分解算法进行改进,可以提高模型的预测精度。

c)对比模型四(CEEMDNA-GS-LSTM)与其他3个模型的预测结果,克服模态混叠和重构误差问题的CEEMDAN-GS-LSTM预测模型预测效果优于EMD-GS-LSTM、EEMD-GS-LSTM预测模型。与模型二相比,其RMSE、MAE和MAPE分别降低了33.65%、27.57%与0.76%,对比模型三,其RMSE、MAE和MAPE分别降低了47.53%、55.99%与2.33%。采用CEEMDAN模态分解算法的预测模型均优于EMD、EEMD,合适的模态分解算法可以更有效地追踪径流时间序列,进而提高模型预测精度。

综上所述,在面对更具波动性的日径流预报中,运用模态分解算法去预测日径流可以提高模型预报精度,且在本文4个模型中,模型四(CEEMDAN-GS-LSTM)模型预报效果优于其他模态分解算法结合LSTM的组合预测模型,CEEMDAN模态分解算法在日径流预报将时间序列自适应地将其分解为一系列不同尺度的模态分量,与EEMD、EMD方法相比,其能实现对幅值较大数据分解的完整性,有利于进一步提高预测精确度。

3 结论

本文针对日径流预报构建了基于CEEMDAN与GS-LSTM的组合预报模型,并对比分析了不同模态分解算法在日径流预报中的影响,通过算例分析得到以下结论。

a)本文首先利用传统模态分解算法EMD和EEMD对径流数据进行分解,再分别对各个模态进行预测,最后对预测值进行重构得到最终的预测值,其预报结果明显优于单一预报模型,EMD-GS-LSTM组合预测模型其RMSE、MAE和MAPE分别降低了625.32%、334.21%与2.12%,EEMD-GS-LSTM组合预测模型其RMSE、MAE和MAPE分别降低了440.15%、42.22%与0.55%,表明将模态分解算法运用日径流预报,可有效提高预报精度。

b)本文所使用的克服模态混叠和重构误差CEEMDAN模态分解算法对日径流进行分解,并使用网格搜索参数寻优算法对LSTM模型的超参数进行优化,其预报结果优于EMD、EEMD模态分解算法,其预报效果较EMD-GS-LSTM组合预测模型,其RMSE、MAE和MAPE分别降低了236.45%、124.68%与0.76%,表明该模型可以更准确地对日径流进行预报。

以“分解-预测-重构”这个径流预报方法而言,模态分解算法的选取将会明显影响到日径流的预报精度,在未来的研究中,改进模态分解算法,对径流时间序列进行更加有效且精准的分解,这将获得更加理想的预测效果。