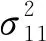具有高阶扰动的Oregonator模型的平稳分布研究
2024-01-05河燕梅文香丹
河燕梅, 文香丹
( 延边大学 理学院, 吉林 延吉 133002 )
0 引言
化学振荡反应是在开放体系中进行的一类远离平衡的反应.由于化学振荡现象广泛存在于化工生产、食品检测和环境保护等多个领域,因此其受到学者们的广泛关注.1974年,Field等[1]基于FKN机制[2]和质量作用定律[3],针对均匀溶液中的振荡化学反应提出了如下Oregonator模型:
(1)
(2)
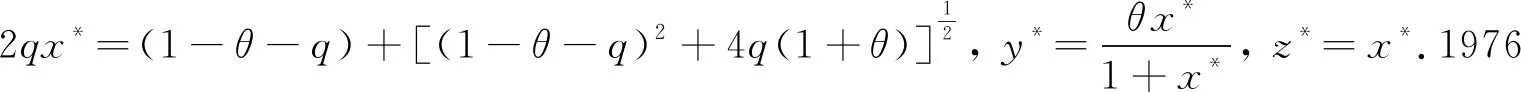
由于化学反应与温度、压力、pH值等因素密切相关,因此用随机微分方程来建立化学反应模型可更好地反映实际现象.2020年,Yang等[5]研究了一种具有线性扰动的Oregonator模型,证明了该系统存在唯一正解,并在此基础上探讨了系统的动力学行为.文献[6-7]的作者研究表明,利用非线性扰动随机微分方程可更好地分析系统的动力学行为.文献[8-11]的作者研究了具有高阶扰动的种群模型和传染病模型.受上述文献启发,本文建立了如下一种具有高阶扰动(又称为非线性扰动)的Oregonator模型:
(3)
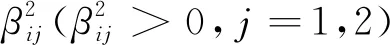
(4)
1 相关引理
引理1(Has’minskii定理)[12]假设存在一个具有正则边界Γ的有界开区域U⊂Rl(Rl表示l维欧几里得空间),且其具有以下性质:
(A1)在区域U及其一些邻域内,扩散矩阵A(x)的最小特征值是非零的.

2 解的平稳分布及其证明
首先证明系统(4)是否存在全局正解.为此,首先给出以下定理.
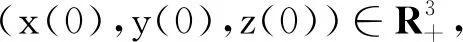
证明由于定理1的证明与文献[5]中的定理2.1类似,故本文在此省略.
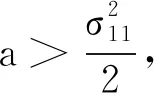
证明为了证明定理2,需首先验证引理1中的条件(A1)和(A2)成立.由系统(4)的漂移项可知,其扩散矩阵为:
由于矩阵A是正定的,因此显然可知条件(A1)成立.
(5)
(6)
L(z)=b(x-z).
(7)
(8)
定义V2=-lny,V3=-lnz.于是对V2和V3分别应用It公式进行计算可得:
(9)
(10)
(11)
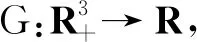
(12)
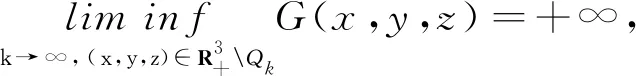

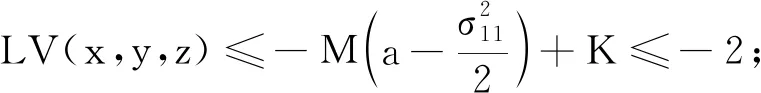
3 数值模拟
本文利用Milstein高阶方法[14]对系统(4)的离散形式进行数值模拟.由文献[14]可知,系统(4)的离散形式为:
其中:时间增量Δt>0,ωij(i=1,2,3)是服从N(0,1)分布的高斯随机变量.在系统(4)中,假设时间单位为min,反应物的浓度为mol/(L·min),初始值为(x(0),y(0),z(0))=(0.8,0.3,0.5),步长Δt= 0.1,其他参数值依据文献[7]分别取a=7.727,q= 0.08375,θ=1,b= 0.161.为了研究不同白噪声强度对系统(4)动力学行为的影响,本文取4组不同的白噪声强度对其平稳分布的存在性进行数值模拟.
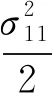
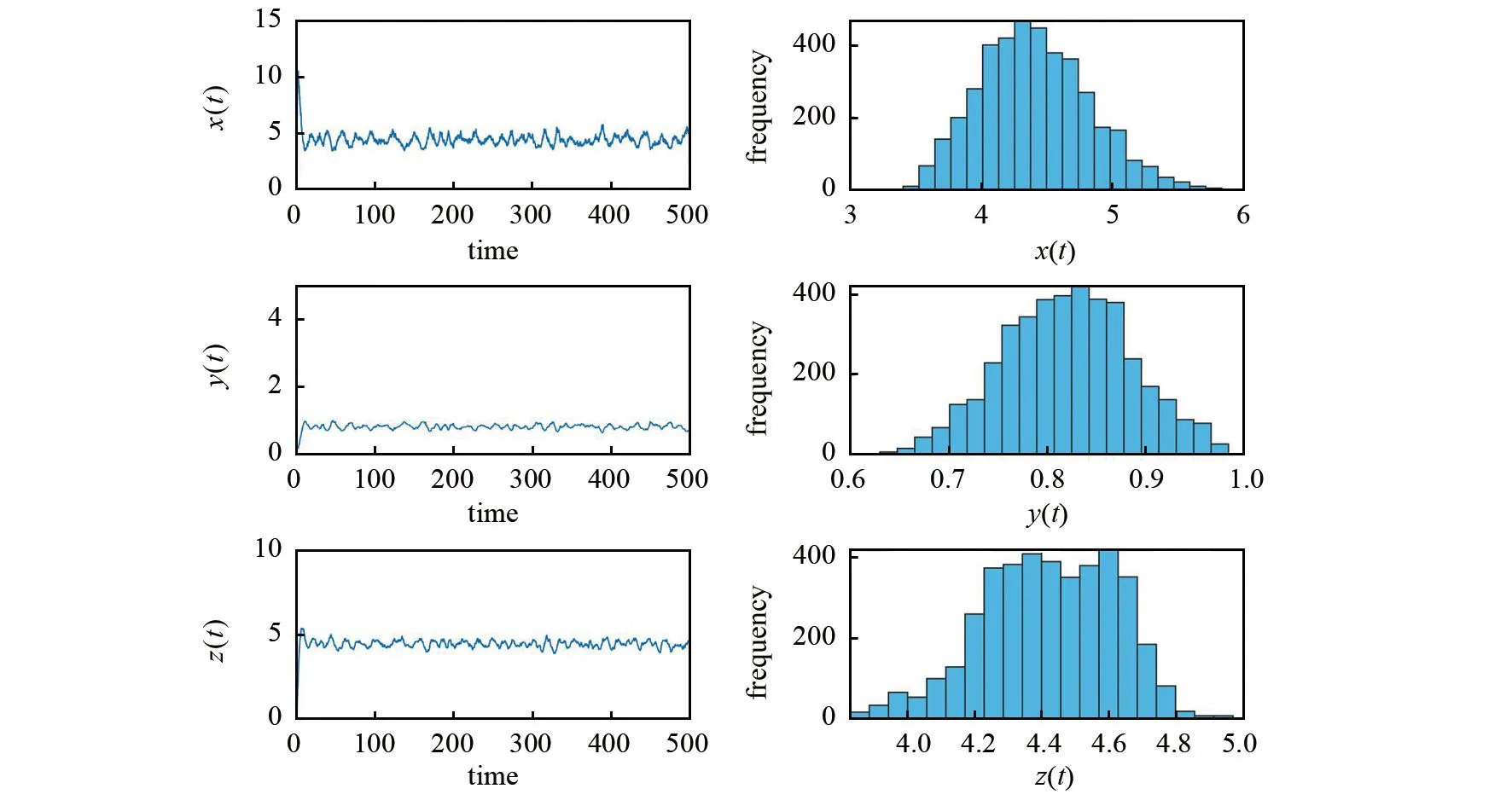
图1 白噪声取σ11= 0.025、σ12= 0.0075、σ21= 0.03、σ22= 0.0025、σ31= 0.0125、σ32= 0.002时系统(4)存在的平稳分布(左图为系统(4)的解,右图为系统(4)的密度函数)
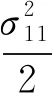

图2 白噪声取σ11= 0.05、σ12= 0.015、σ21= 0.06、σ22= 0.005、σ31= 0.025、σ32= 0.004时系统(4)存在的平稳分布(左图为系统(4)的解,右图为系统(4)的密度函数)
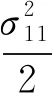

图3 白噪声取σ11= 0.1、σ12= 0.03、σ21= 0.12、σ22= 0.01、σ31= 0.05、σ32= 0.008时系统(4)存在的平稳分布(左图是系统(4)的解,右图是系统(4)的密度函数)
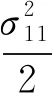
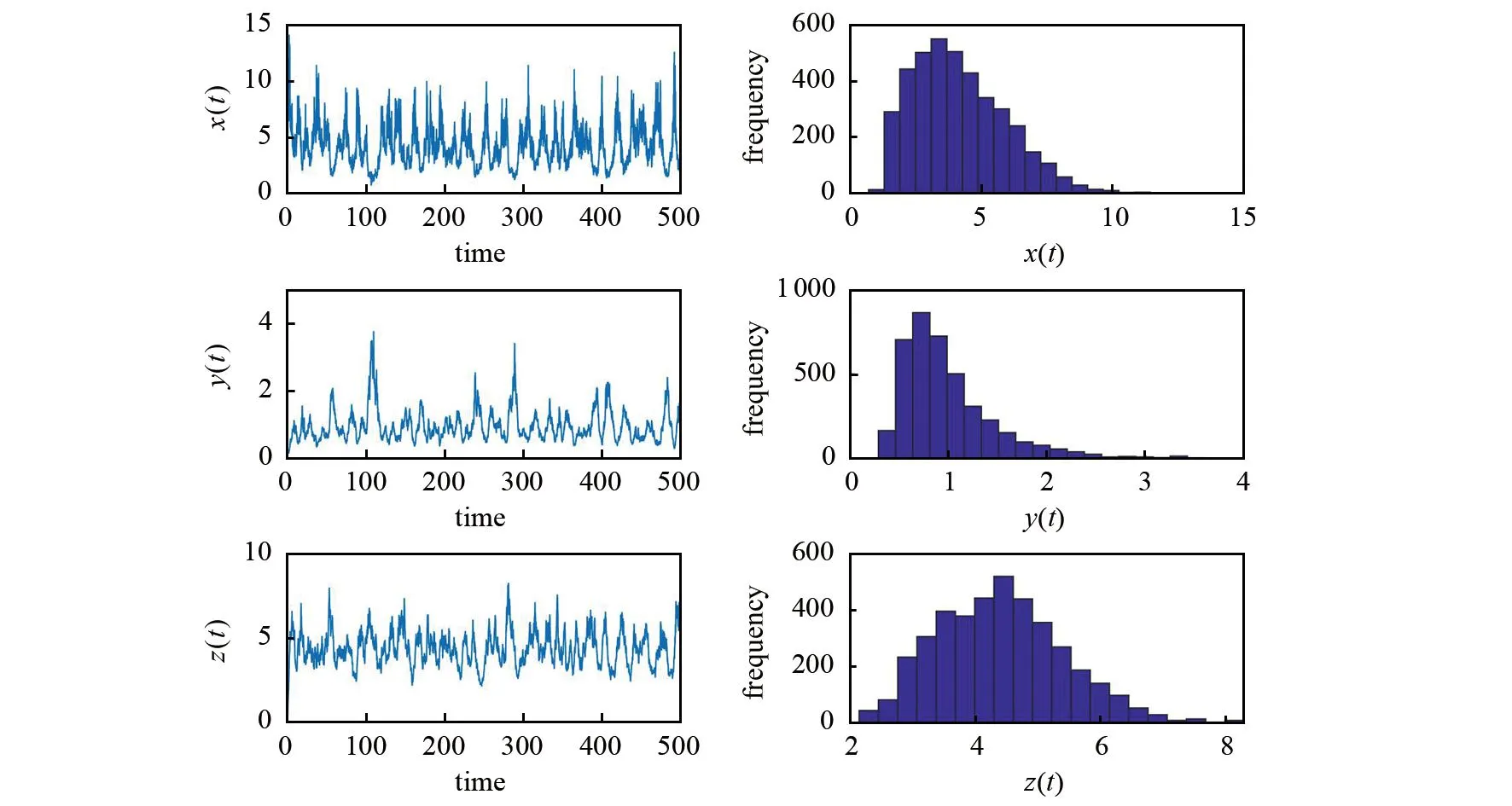
图4 白噪声取σ11= 0.15、σ12= 0.045、σ21= 0.18、σ22= 0.015、σ31= 0.075、σ32= 0.012时系统(4)存在的平稳分布(左图是系统(4)的解,右图是系统(4)的密度函数)
由图1—图4可以看出,白噪声强度越小,系统解的振荡幅度越小.另外,本文以3)中的白噪声为例,给出了3个系统(非线性系统(4)与其相对应的确定性系统(2)、线性系统(13))解的运行图.由图5中的(a)和(c)可以看出,系统(4)的解在系统(2)解的附近振荡;由图5中的(b)和(c)可以看出,系统(4)的解的振荡幅度大于线性扰动系统(13)的振荡幅度.上述结果表明,非线性扰动系统(4)的解大幅偏离了原系统的平衡状态.
(13)
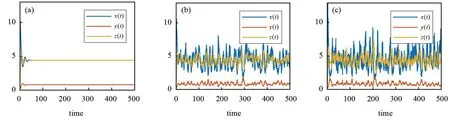
图5 白噪声取σ11= 0.1、σ12= 0.03、σ21= 0.12、σ22= 0.01、σ31= 0.05、σ32= 0.008时不同系统的解((a)为系统(2)的解,(b)为与系统(2)相对应的线性扰动系统(13)的解,(c)为与系统(2)相对应的非线性扰动系统(4)的解)
4 结论