复杂环境下AGVS 路径规划算法

姚道金 殷雄 罗真 温锐 陈智宇 邹鸿昊

（华东交通大学 电气与自动化工程学院，江西 南昌 330013）

近年来，自动导向搬运车系统（AGVS）已成为研究的热点，其中AGVS 路径规划是研究热点之一。AGVS 是由多个同构或异构机器人组成的自动导向搬运车系统，通过控制机器人协同完成作业任务［1］。相比单机器人，AGVS 具有可同时执行多个任务、工作范围大、作业集群化和规模化等优点。但随着机器人数量的增加，路径规划算法的复杂度也呈指数上升。目前，AGVS 路径规划大多使用分层分布式框架，分为下层路径规划和上层协同规划，下层路径规划为各机器人寻找最优路径，而上层协同规划考虑机器人之间优先级，完成机器人等待、避让等任务［2］。

路径规划算法通常可分为图搜索算法和智能优化算法，其中图搜索算法对地图栅格化后进行筛选，生成最优路径，包括Dijkstar 算法［3］、A*算法［4］、JPS 算法［5］等；智能优化算法包括人工势场法［6］、蚁群算法［7］、灰狼算法［8］等。

针对路径规划问题，许多学者进行了大量研究，文献［9］提出了一种双层路径规划算法，算法第一层为融合路径信息动态权重因子和Bezier 曲线的改进A*算法，第二层引入时间维度，建立机器人路径时间图，从而预测机器人之间的冲突。文献［10］提出了一种AGVS协同规划策略，首先使用协同进化粒子群优化算法部署传感器位置，然后使用改进K-means 方法划分任务区域，最后以传感器位置为路径点规划路径。文献［11］提出了一种多机器人多任务点协同巡检方法，首先使用改进的生物激励神经网络算法对多任务点进行巡检，然后将电站区域分解成若干不含障碍物的子区域，各移动机器人分别在子区域内利用优先级启发式算法选择路径。文献［12］提出了一种多机器人协同路径规划方法，首先生成预约表，然后生成加权地图，最后通过分布式控制方法对多机器人协同路径进行规划。文献［13］提出了一种基于改进DWA的多机器人编队控制算法，首先对传统DWA算法进行改进，然后为机器人设计不同的行为，最后基于改进DWA和社会力模型设计行为控制策略，使领航者在未知环境下能够规划适合整体编队运行的路径，跟随者能够根据编队的不同状态自适应地切换跟随方式。以上算法均取得了较好的规划效果，但没有同时考虑静态地图中出现的临时静态障碍物和动态障碍物，未能有效地解决复杂环境下AGVS的路径规划问题。

为此，文中提出了一种分层分布式框架下改进的AGVS 路径规划算法，该算法分为两层，第一层引入混合改进A*算法和DWA算法，实现单机器人的路径规划；第二层引入协同规划，考虑机器人之间的协调运动，实现AGVS 路径规划。最后在Matlab中进行仿真实验，以验证所提算法的有效性。

1 算法整体框架

AGVS路径规划框架主要有3类：集中式框架、分布式框架和分层分布式框架［14］。文中算法使用的分层分布式框架具有集中式框架和分布式框架的优点［15］，保留了单个移动机器人路径规划的独立性，同时各机器人接受统一规划任务控制。算法整体框架如图1所示。

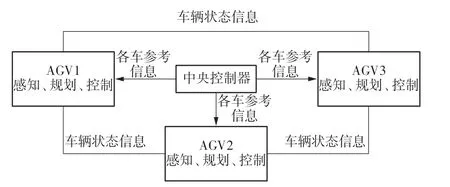
图1 分层分布式框架Fig.1 Hierarchical distributed framework

2 路径规划

2.1 改进的A*算法

传统A*算法的搜索步骤如下：首先将起始点Xstart加入open 列表，同时将起始点Xstart作为父节点加入close 列表；然后搜索起始点Xstart的相邻（非障碍物）节点并加入open 列表，依据评价函数f（n）=g（n）+h（n）计算open 列表中节点代价，选取代价最低节点作为下一个父节点，并将其放入close 列表；最后搜索父节点的可达节点并计算代价，重复上述过程，直至父节点为目标点Xgoal为止［16］。其中g（n）为当前节点到起始点Xstart的距离，h（n）为当前节点到目标点Xgoal的距离，采用欧几里得距离，即

式中，nx、ny为当前节点在x、y轴上的坐标值，gx、gy为目标点在x、y轴上的坐标值。

2.1.1 改进的评价函数

由于评价函数估计值与栅格地图实际值相差很大，导致传统A*算法的搜索效率低。因此，可对传统A*算法的评价函数进行改进，由于h（n）为欧几里得距离，且h（n）始终小于实际距离，故可为h（n）增加权重系数，得到改进后的评价函数为

式中，r为当前点到目标点的距离，R为起始点到目标点的距离。

2.1.2 双向Floyd算法

传统A*算法生成的路径中含有大量的冗余点，路径不平滑。目前，常用的路径优化算法有Floyd算法、贝塞尔曲线和B 样条等。Floyd 算法作为一种基于动态规划方法的最短路径算法，又被称为插点法［17］。传统Floyd 算法仅对起始点Xstart至目标点Xgoal的路径进行优化。为此，文中提出了一种双向Floyd 算法，增加了对目标点Xgoal至起始点Xstart的反向轨迹进行优化，实现双向轨迹优化，以进一步提高路径平滑度，具体原理如图2所示。

图2 改进Floyd算法去除路径冗余点原理Fig.2 Principle of the improved Floyd algorithm to remove path redundancy points

图2 中，改进Floyd 算法先去除路径冗余点，路径变为Xstart→X1→X2→X3→Xgoal；然后进行正向轨迹优化，路径变为Xstart→X4→Xgoal；最后采用与正向轨迹优化相同的方式进行反向轨迹优化，路径变为Xstart→X5→Xgoal。

双向Floyd算法加入了障碍检测，计算障碍物中心与路径间的垂直距离，避免路径与障碍物相交。障碍物距离计算方法如图3所示，设路径起始点Xstart的坐标为（xA，yA），路径目标点Xgoal的坐标为（xB，yB），XstartXgoal与x轴之间的夹角为α，障碍物中心点C的坐标为（xC，yC），d为点C至点Xstart的垂直距离，e为点C至点Xgoal的纵向距离，则障碍物与路径XstartXgoal之间的距离d可由点Xstart、Xgoal、C的坐标表示为

图3 障碍物距离示意图Fig.3 Schematic diagram of obstacle distance

2.2 改进的DWA算法

DWA 算法是一种常见的移动机器人局部路径规划算法，将移动机器人建立在速度空间中，具体步骤如下：首先对移动机器人建立运动学模型，采集多组速度，通过建立的运动学和速度模型对其一段时间内的运动轨迹进行分析和预测；然后使用DWA算法的评价函数选出最优轨迹及对应的速度；最后根据选出的最优轨迹段及其对应的速度组进行局部路径规划［18］。

2.2.1 机器人初始位姿

针对目标点方位，可以改进起始点机器人的初始位姿［19］。若机器人的初始位姿方向与目标点方向相差太多，则需要机器人绕幅度较大的弯来完成位姿矫正，这将极大增加路径转弯次数，同时耗费时间。因此，文中对起始点位姿进行优化，若机器人起始点位姿θ大于45°，则给定一个角加速度a进行位姿优化：

式中，θ为初始航向与起始点到目标点连线的夹角（如图4所示），ΔT为位姿优化时间。

图4 机器人起始位姿调整Fig.4 Robot starting posture adjustment

2.2.2 机器人运动学模型

移动机器人运动模型分为差速驱动机器人模型和全向移动机器人模型。文中建立差速驱动机器人模型，通过调节左、右轮驱动速度控制机器人运动。运动学建模过程中，对线速度和角速度进行采样，得到机器人在一段时间内进行匀速运动的模型：

式中，v（t）为当前线速度，ω（t）为当前角速度，Δt为计算时间，θt为机器人当前位姿角度。

2.2.3 机器人运动速度范围

移动机器人在速度空间中，由于自身模型限制、硬件上限和环境约束，需要对理论上存在的无穷多速度组进行约束。设移动机器人受自身条件制约的最大线速度为vmax、最大角速度为ωmax、最小线速度为vmin和最小角速度为ωmin，则机器人线速度v和角速度ω组成的速度空间可表示为

差速机器人靠电机驱动，存在速度约束。在DWA算法中，机器人模型受加速度影响的线速度v和角速度ω范围为

式中，vt为t时刻的线速度，为加速度，ωt为t时刻的角速度，为角加速度。

DWA 算法中评价函数选取最优轨迹和对应的速度组，选择标准为躲避障碍物、距离最短、靠近目标点，具体公式为

式中，dist（v，ω）为模拟轨迹与最近障碍物的距离。

2.2.4 改进的DWA算法的评价函数

DWA 算法需要为机器人建立评价函数，对模拟出的机器人若干运动轨迹进行评估择优。传统DWA算法的评价函数head（v，ω）是轨迹终点方向与目标点之间的角度差，但文中DWA 算法是在全局路径规划基础上运行的，因此，需要改进角度差评价函数，增加一个当前目标加权系数P，改进的DWA算法的评估函数为

式中，vel（v，ω）为速度评价子函数，σ为平滑函数，δ、β和γ为各评价子函数的加权系数。

2.3 算法融合

两种改进算法融合的具体步骤为：首先，使用改进的A*算法生成移动机器人的全局最优路径；然后，将最优路径中的关键节点分配给改进的DWA算法，由改进的DWA算法进行局部路径规划；最后，移动机器人沿着最优路径，有效躲避静态障碍和动态障碍。

3 协同规划

AGVS 协同规划是减少机器人之间发生冲突的关键。协同规划主要包括设置优先级和设置冲突协调策略两部分［20］，以提高AGVS规划算法的鲁棒性。

3.1 设置优先级

优先级法是指在AGVS 系统中为移动机器人进行等级排序［21］。当机器人之间发生冲突时，优先级高的机器人拥有指挥权和调配权，从而控制优先级低的机器人，避免机器人之间发生冲突。优先级法中优先级分配是关键，直接影响冲突协调结果。文中根据3 个机器人（AGV1、AGV2、AGV3）执行任务顺序，将优先级设置为AGV1 ≥AGV2 ≥AGV3。

3.2 设置冲突协调策略

冲突协调策略包括等待行为和避让行为。等待行为指机器人之间距离小于危险距离时，低优先级机器人将保持原位置等候，直至冲突结束。避让行为指机器人之间距离小于危险距离时，低优先级机器人在原位置等候，而高优先级机器人则使用改进的DWA算法重新规划路径，避让低优先级机器人，直至冲突结束。具体冲突协调策略如下：

（1）协调策略1 针对全局路径规划，通过优先级策略判断冲突机器人的优先级大小。高优先级机器人完成路径搜索后，再由低优先级机器人搜索，最后生成所有机器人的全局最优路径。

（2）协调策略2 针对局部路径规划，将机器人危险距离设置为3 m，当AGV1航向角与AGV2航向角的夹角小于100°时，低优先级机器人发生等待行为，高优先级机器人按照原路径前进，直至冲突结束；当AGV1 航向角与AGV2 航向角的夹角大于100°时，低优先级机器人发生等待行为，高优先级机器人发生避让行为，直至冲突结束。

4 算法仿真与结果分析

为验证文中改进算法的可行性和有效性，在30 m×30 m 含障碍物地图环境中进行路径规划。运行环境为：Matlab R2022a、Windows10 64bit、处理器（Intel）i5-12400F 12代、内存32 GB。

传统A*算法与改进A*算法规划的路径及其长度对比如图5 和表1 所示。从图中可以看出，改进A*算法的路径冗余点明显减少，且路径与障碍物保持安全距离。由表中可知，由改进的A*算法生成的路径长度平均缩短了2.26%。

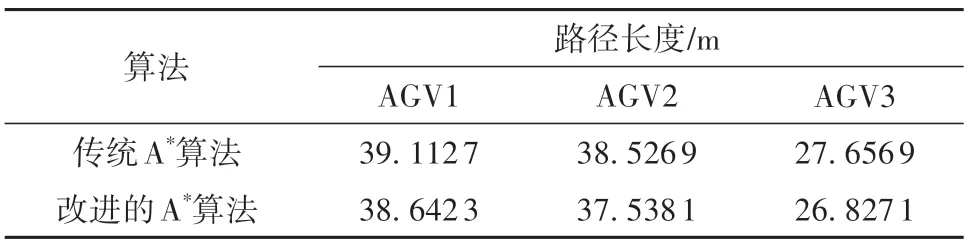
表1 两种算法生成的路径长度对比Table 1 Length comparison of paths generated by two algorithms

图5 两种算法生成的路径比较Fig.5 Comparison of paths generated by two algorithms

图6 为文中算法的AGVS 完整路径规划结果，图中有3个圆形机器人、数个黑色静态障碍物、3个移动障碍物和1 个灰色临时障碍物。由图中可知，AGVS可在简单环境中完成无碰撞路径规划。

为进一步验证文中算法的鲁棒性，更改地图环境，再进行AGVS路径规划，仿真结果如图7所示。由图中可知，3 个移动机器人均能顺利到达目标位置，未与障碍物发生碰撞，这表明，文中算法可以适应地图环境的变化，具有较强的鲁棒性。

文中算法的AGVS 位姿、角速度和线速度曲线如图8 所示。由图8（a）可知，改进的DWA 算法可以有效地调整机器人的初始位姿，使机器人沿着全局最优路径前进。由图8（b）和图8（c）可知，AGVS运动过程中，机器人的角速度始终保持在-0.4～0.4 rad/s 区域内，AGVS 线速度保持在0.6～1.2 m/s区域内，符合机器人运动学特性。文中提出的AGVS 路径规划算法可以使多个移动机器人平滑运动到目标位置，在避免AGVS间冲突的同时，生成最优的平滑路径。

图8 文中算法的AGVS位姿、角速度和线速度曲线Fig.8 Pose，angular velocity and linear velocity curves of AGVS by the proposed algorithm

图9 为AGVS 冲突协调策略的作用效果。当AGV1和AGV2发生冲突，根据协调策略，AGV2速度预测轨迹消失，暂停等待AGV1，当AGV1离开后，AGV2 开始运动，证明了文中提出的算法可以有效地解决机器人之间的冲突问题。

图9 AGVS冲突协调策略的作用效果Fig.9 Effect of AGVS conflict coordination strategy

5 结论

文中提出了一种分层分布框架下改进AGVS 路径规划算法，以解决复杂环境下AGVS的路径规划问题。该算法分为下层路径规划和上层协同规划，下层路径规划为融合改进A*算法的全局规划和改进DWA算法的局部规划；上层协同规划在机器人优先级分配的基础上加入冲突协调策略，以实现AGVS在复杂环境下的路径规划。仿真结果表明，文中改进算法可得到复杂环境下机器人的无碰撞最优路径，路径长度比传统A*算法的机器人路径缩短2.26%。

文中提出的算法实现了复杂环境下AGVS 的路径规划，但缺少任务分配和作业区域自主分配。未来工作主要集中在：①对AGVS任务进行自主分配，增加单机器人执行任务的数量；②对机器人作业区域进行有效分配，对分配区域进行自主路径规划。