移动荷载作用下变截面连续箱梁桥的约束扭转效应研究
2024-01-04王伟
王 伟
(中铁十八局集团第一工程有限公司,河北省保定市涿州市冠云路86号 072750)
随着我国基础设施建设的发展和交通行业的需要,桥梁工程越来越多[1-3]。而钢筋混凝土连续箱梁桥是一种常见的桥梁形式,许多人对此进行了一系列研究[4,5]。
王来永等[6]通过理论计算和模型试验的方法,对斜拉体系加固大跨径箱梁桥的关键构造受力性能进行了研究。于利存等[7]通过车桥耦合振动测试和室内试验,对连续箱梁桥的拼接缝浇筑方式进行了分析,结果表明微差浇筑施工工艺经济性较好,且受力合理,表现出了良好的应用性。杜连玉和李兆霞[8]基于极限应变理论,提出了一种新的连续箱梁桥构件的易损性评估方法,对不同荷载分布形式作用下的构件重要性系数进行了计算。孙恒[9]通过有限元数值模拟方法,对宽幅箱梁桥的偏载系数进行了研究,分析了偏载系数沿箱梁纵向的变化规律。唐星宇和郭增伟[10]亦通过有限元方法,研究了箱梁桥支架布置形式的优缺点,结果显示轴线平行式布架方式效果较好。方圣恩和唐永久[11]以实际工程为例,研究了隔震支座对混凝土箱梁桥地震易损性的影响。裴元江等[12]基于FAHP-云模型,对预应力钢筋混凝土箱梁桥的施工风险进行了研究,并提出了一系列控制措施。
为研究变截面箱梁桥的应力分布特征和变形规律,文中根据箱梁约束扭转微分方程,推导出了变截面箱梁单元刚度矩阵。基于此,依托跨四港联动大道项目进行实例分析,设置了3种荷载分布工况,计算出了不同工况下变截面箱梁的弯矩和翘曲位移,并对应力放大效应进行了探究。
1 约束扭转控制微分方程
薄壁箱梁扭转变形计算,在乌曼斯基第二理论中,扭转角θ(z)控制方程如下:
(1)

在(1)式中,齐次微分方程的初参数解如下:
(2)
(3)
(4)
T(z)=T0
(5)
式中,β′(z)表示广义翘曲位移;B(z)表示翘曲双力矩;T(z)表示扭矩;G表示剪切模量;Id表示抗扭惯性矩。此外,θ0,β0,T0和B0是4个初始参数,当z=0时,θ0表示扭转角,β0表示广义翘曲位移,T0表示扭矩,B0表示翘曲双力矩。
确定以上4个初始参数,需要对边界条件进行定义。端点为自由端时,T=0,B=0;端点为简支端时,θ=0,B=0;端点为固定端时,θ=0,β′=0。
2 单元刚度矩阵
依据约束扭转微分方程解对箱梁单元刚度矩阵进行了推导。图1展示了箱梁单元,C表示箱梁截面的形心,S表示箱梁截面的扭转中心。在研究中,将扭转中心设为坐标原点,对约束扭转效应进行分析。
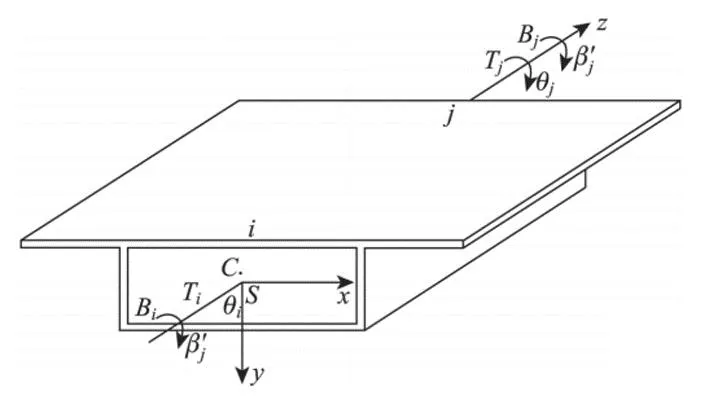
图1 箱梁单元Fig.1 Box girder unit
根据有限元理论,单元平衡方程如下:
F=Kδ
(6)
(7)
式中,F表示单元节点力列阵;δ表示结点位移列阵;K表示单元刚度列阵。

(8)
3 应力放大系数
分析空间效应时,通常将作用于箱梁上的偏心荷载分解为对称荷载和非对称荷载进行简化。通过梁的弯曲理论求解对称荷载作用下的竖向挠曲,通过箱梁扭转理论求解反对称荷载作用下的扭转,最后对计算结果进行叠加。
约束扭转效应会对应力产生放大效果,为表示这种放大效应,引入了放大系数η,计算公式如下:
(9)
式中,σm表示正对称荷载作用下的弯曲正应力;σω表示反对称荷载作用下的扭转翘曲正应力。
4 实例分析
依托跨四港联动大道项目进行实例分析,该项目为(45+80+45)m,3跨变截面预应力钢筋混凝土连续箱梁桥。桥墩采用花瓶型桥墩,材料为C40混凝土。基础采用钻孔灌注桩,成孔方式采用机械钻孔,钻孔桩直径为1m、1.2m和1.5m,3种桩径,承台为C30混凝土,承台埋深在地面或设计地面道路以下不小于0.5m。施工采用碗口架分段现浇方案。跨中梁高度为2m,顶板宽度为17m,底板宽度为9m,翼缘板悬臂端长度为4m。车道荷载为公路Ⅰ级,计算弹性模量设为34GPa,剪切模量设为14.5GPa。设置3种加载工况,如图2所示,其中P1为集中荷载,q为均布荷载。该箱梁桥为变截面连续箱梁桥,中跨跨中截面尺寸见图3。

(a)工况一

图3 中跨跨中横截面(单位:cm)Fig.3 Mid-span cross-section(unit:cm)
在偏载作用下,箱梁发生空间效应,由弯曲正应力和翘曲正应力组成箱梁截面正应力。根据前人研究,相较于翘曲正应力,弯曲正应力占比更大。因此,布载方式选择弯曲效应最显著的方式,即4车道布载进行考虑。这种布载方式也与实际最为相符,偏心距经过计算后为1.95m。根据相关规范[13]对荷载进行折减,折减后均布荷载q为28.14kN/m,集中荷载P1为965.2kN/m,P2为942kN/m。
通过自编程进行了计算。图4展示了3种工况下的弯矩曲线。从图中可以看出,工况1和工况2中弯矩随纵向距离变化曲线数值和趋势均较为类似,呈现出“W”型。相较于前两者,工况3变化趋势恰好相反,近似呈现出“M”型,且数值和变化幅度方面均偏小。这是由于工况1和工况2在跨中设有集中荷载和均布荷载,导致跨中下侧受拉,即弯矩表现为正。工况3荷载主要分布在边跨,跨中无荷载施加,因此在两端箱梁下侧受拉,传递到跨中后为上侧受拉,表现为负弯矩。
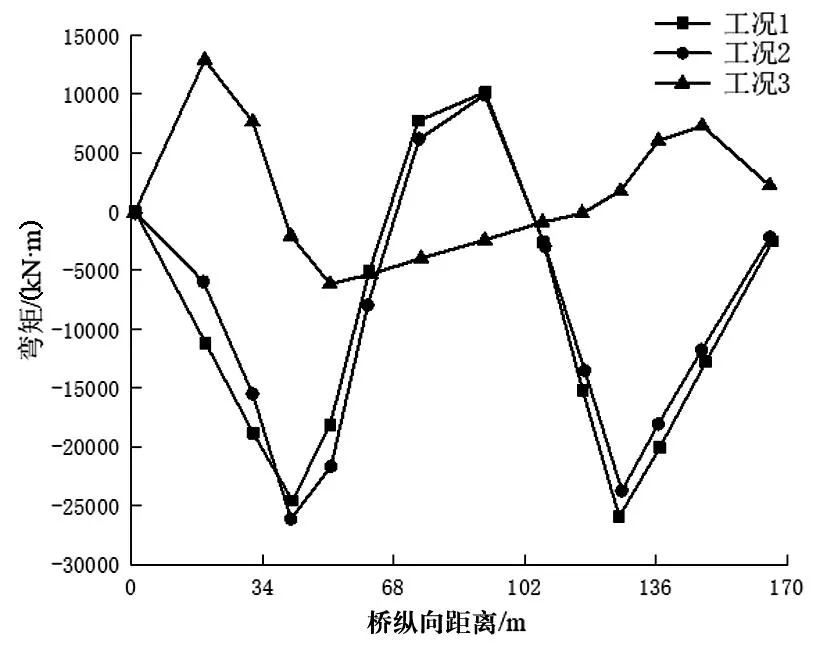
图4 弯矩曲线Fig.4 Bending moment curve
图5展示了3种工况下的广义翘曲位移曲线。从图中可以看出,翘曲位移主要集中在边跨端部和跨中位置处,以跨中截面为界表现出反对称分布。工况1和工况2中广义翘曲位移在箱梁桥左跨存在一定差异,在中跨及右跨数值和变化趋势基本一致,这是由于两者在左跨施加荷载不同导致的。与工况1和工况2相比,工况3左跨位移更大,这是由于在工况3中不仅施加均布荷载于左跨,同时还伴有集中力的作用。而由于跨中无荷载施加,工况3跨中位移较小。

图5 广义翘曲位移曲线Fig.5 Generalized warping displacement curve
图6展示了3种工况下的双力矩曲线。观察图6可以发现,翘曲双力矩曲线呈现出由峰值点向两侧衰减的规律。3种工况下,在中支点位置处和集中荷载作用点处均出现极值,因此可以表明,集中荷载和支座约束会对翘曲双力矩产生较大的影响。
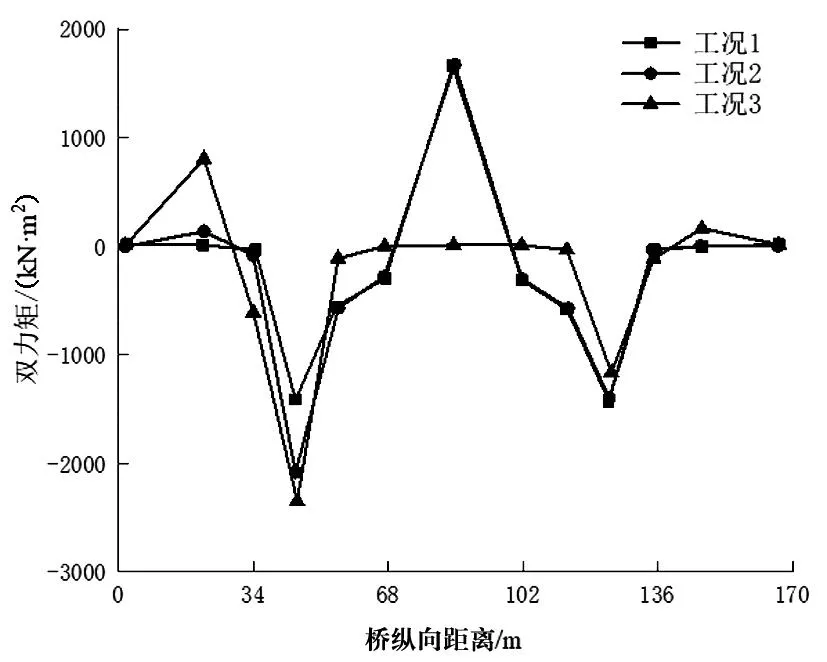
图6 双力矩曲线Fig.6 Double moment curve
对截面上各点的弯曲正应力和翘曲正应力进行了计算。由于受到篇幅限值,计算弯曲正应力时,仅考虑到了工况1;计算翘曲正应力时,仅计算了工况1和工况2。
图7展示了工况1的弯曲正应力曲线。从图中可以看出,工况1中箱梁顶板和底板的弯曲正应力均沿跨中截面对称分布。顶板方面,弯曲正应力极值出现在每一跨的跨中位置,两端弯曲正应力为正,跨中为负。与顶板相比,底板弯曲正应力符号与变化趋势恰好相反,弯曲正应力峰值为跨中截面,变化幅度更明显。这也是由于,箱梁主要承受上部荷载,下部受弯程度更甚,导致下部承受的弯曲应力更大,因此,应采取必要的加固设计。
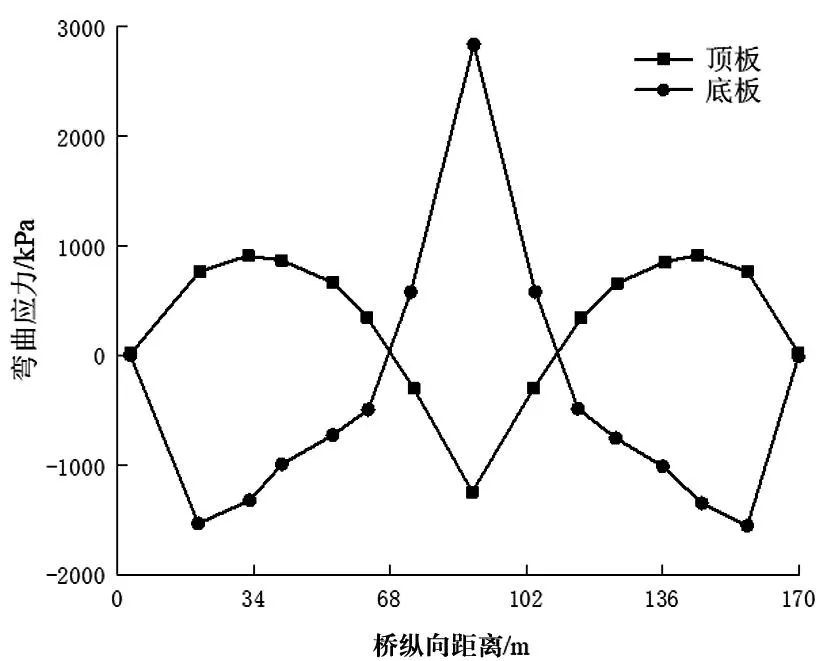
图7 工况1弯曲正应力曲线Fig.7 Bending normal stress curve under working condition 1
图8展示了工况1和工况2的翘曲正应力曲线。从图8(a)和图8(b)中可以看出,工况1中的翘曲应力亦呈现出关于跨中截面对称的分布态势。且2种工况下翘曲正应力极值均出现在集中荷载作用的截面。最大翘曲应力正值出现在了底板与腹板交点位置处,而最大负值出现在了顶板与腹板交点位置处。

(a)工况1
在分析偏载作用下箱梁应力放大系数时,通常选取控制截面,再通过控制截面进行可变荷载内力增大系数的计算。计算了3种工况下中支点、中跨跨中、中跨1/4处和边跨跨中截面的应力放大系数,计算结果见表1。

表1 应力放大系数
从表1中可以看出,工况1荷载分布下,应力放大系数最大的为中跨1/4截面,达到了1.22,而边跨跨中应力未发生放大效应,因此应力放大系数为1.0。工况2荷载分布下,应力放大系数最大的为中支点截面,达到了1.14,中跨跨中截面和中跨1/4截面与中支点截面均较为接近,为1.13,最低的为边跨跨中,应力放大效应甚微,为1.01。工况3荷载分布下,应力放大系数分布较为突出,中支点截面应力放大系数为1.41,而在其他控制截面处,应力放大效应不明显,放大系数均接近1.0。3种工况下,应力放大系数在1.0~1.41之间,与前人的研究也较为相符,体现出了计算结果的可靠性。
5 结论
文中基于箱梁约束扭转微分方程,考虑到了箱梁截面几何特征值,对变截面箱梁单元刚度矩阵进行了推导。依托跨四港联动大道项目进行实例分析,设置了3种荷载分布工况,计算出了不同工况下变截面箱梁的弯矩和翘曲位移,并对应力放大效应进行了探究。得出主要结论如下:
1)工况1和工况2中弯矩随纵向距离变化曲线数值和趋势均较为类似,呈现出“W”型。工况3变化趋势恰好相反,近视呈现出“M”型,且数值和变化幅度方面均偏小。
2)翘曲位移主要集中在边跨端部和跨中位置处,以跨中截面为界表现出反对称分布。工况1工况2中广义翘曲位移在箱梁桥左跨存在一定差异,在中跨及右跨数值和变化趋势基本一致。
3)翘曲双力矩曲线呈现出由峰值点向两侧衰减的规律,在中支点位置处和集中荷载作用点处均出现极值,说明集中荷载和支座约束会对翘曲双力矩产生较大的影响。翘曲正应力极值均出现在集中荷载作用的截面。最大翘曲应力正值出现在了底板与腹板交点位置处,而最大负值出现在了顶板与腹板交点位置处。
