不同部件变形对转管机枪枪口扰动的影响分析

王晓峰,薛百文,杨 臻,秦叔敏,刘朋展,张光祥

(1.中北大学 机电工程学院, 太原 030051;2.中国北方车辆研究所, 北京 100072)

0 引言

枪口扰动是影响武器射击精度的重要因素[1],与武器的作战威力密切相关。转管机枪武器系统处于工作状态时,身管因高速旋转而产生变形;支架、摇架和托架因射弹过程中产生的后坐力而产生变形,二者均会造成枪口扰动,进而影响武器系统的射击精度[2]。

转管机枪在射击过程中受力部件及身管的变形和机构振动等是影响枪口参数的主要影响因素。其中文献[4-8]对转管机枪在不同射频、不同路面条件、不同车速条件等方面分析了车载转管机枪的发射动力学仿真;文献[9-11]从转管机枪的架体优化、不同射角下对架体的影响、射击密集度等方面进行了分析。以上文献均采用了虚拟样机刚柔耦合模型,研究了多部件柔性化分析,但不同的受力部件在射弹过程中均会产生变形,且受力部件的变形量不同,鲜有人分析不同的单一受力部件对枪口的影响。

本文中以某外能源转管机枪武器系统为研究对象,转管机枪武器站为平台,通过建立刚柔耦合虚拟样机模型,对转管机枪不同单一受力部件作为柔性体进行仿真,并与多部件作为柔性体的仿真工况进行比对,分析了转管机枪射弹过程中的不同部件对枪口扰动的影响程度及规律,为该转管机枪武器系统的进一步改进优化提供了理论基础。

1 多体系统动力学理论

多体系统动力学是研究多体系统(一般由若干个柔性和刚性物体相互连接所组成)运动规律的科学。通过相对坐标系方法和绝对坐标系方法建立数学模型。

多体系统的建模方法虽然各异,但最后形成的系统方程主要为2类,一类为纯微分方程如式(1)所示。一类为微分代数方程(differential algebraic equations,DAEs)如式(2)所示[3]。

(1)

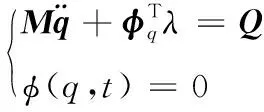
(2)

式(1)—式(2)中:q为广义坐标列向量;M为广义质量矩阵;Q为广义力向量;φ为约束代数方程;φq为约束方程对应的雅克比矩阵。

微分—代数方程的求解方法主要分为缩并法和增广法两大类。缩并法,就是釆用适当的算法将系统中的独立变量和非独立变量分开,将系统方程转化为纯微分方程。

增广法是把拉格朗日乘子和广义坐标加速度作为未知量同时求解,然后根据加速度积分求解广义坐标和广义速度,主要有直接积分法和约束稳定法。

刚柔耦合系统方程一个突出的特点就是大范围刚体运动与小弹性变形之间的耦合导致系统动力学方程为刚性方程,求解刚性方程主要的方法有向后差分法(BDF)为代表的线性多步法和隐式龙格-库塔方法。线性多步法充分利用前步的计算结果,比龙格库塔法计算量小很多,计算速度快。在求解多体系统动力学过程中,一般需要求解非线性方程组,主要釆用牛顿-拉夫逊迭代求解。

2 转管机枪刚柔耦合模型的建立

通过ug建立三维实体模型,为减小计算量,进行模型简化,保留其主要特征,将简化后的x_t模型导入Adams建立虚拟样机模型。文中转管机枪在射弹过程中支架、摇架、托架和身管均会产生变形,但身管变形主要影响因素是身管组的高速旋转,受力架体主要影响因素为射弹过程产生的后坐力,因此将身管作为柔性体,分别将支架、摇架和托架依次作为柔性体进行仿真计算。建立5种工况进行仿真,仿真工况如表1所示。

表1 5种仿真工况

2.1 基本假设

1) 以武器站体为平台进行仿真,假设武器站体—地面为刚性连接。

2) 弹丸击发产生的后坐力通过直接添加膛底合力来代替。

3) 忽略机心组中机头、击针等部件运动,仅使行星体做旋转运动。

4) 忽略安装间隙以及加工误差带来的影响,零部件均以名义尺寸建立模型。

5) 不考虑击发时枪口的切向速度与击发延迟时间。

6) 以枪口处卡箍端面中心代替枪口中心,下文中枪口均指此枪口中心[12]。

2.2 边界条件

转管机枪武器系统的主要运动为外能源驱动电机带动传动齿和身管组旋转,进而带动自动机旋转完成自动循环过程。虚拟样机中,坐标系采用右手坐标系,以枪口轴向方向为y轴正向,竖直向下为x轴正向。虚拟样机示意图如图1所示。

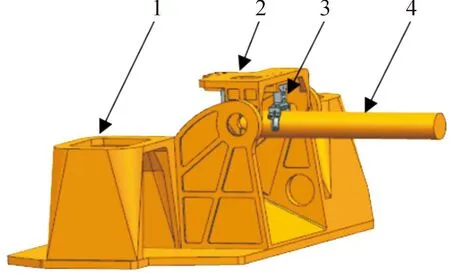
1.托架;2.摇架;3.支架;4.身管组

仿真模型根据转管机枪的物理约束关系,添加约束副进行仿真,主要部件约束副如表2所示。

所有仿真工况均以射频2 000发/min进行仿真计算。

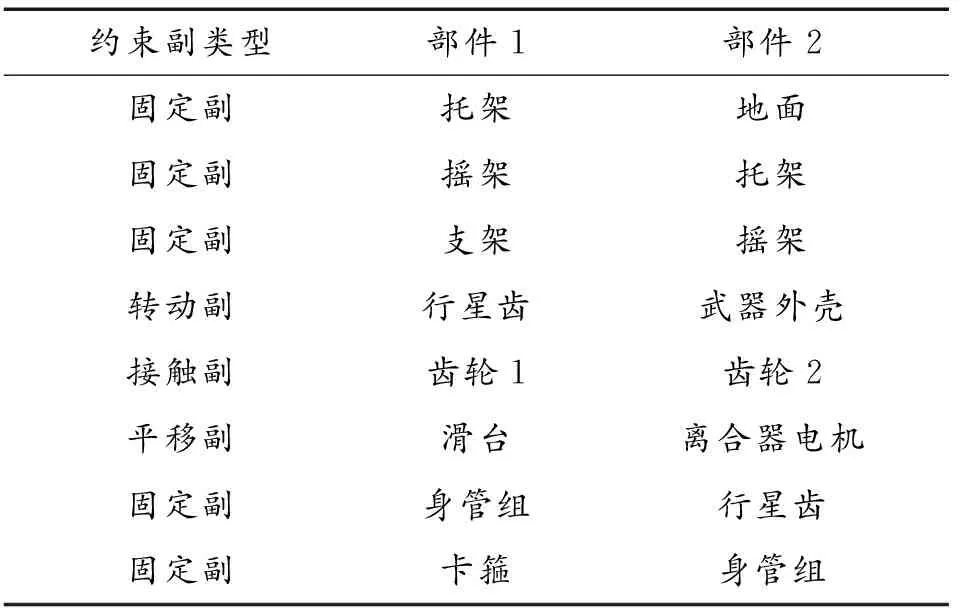
表2 主要部件约束副关系

2.3 柔性体表示及建立

柔性模块采用模态来表示物体弹性,它基于物体的弹性变形是相对于连接物体坐标系的弹性小变形,同时物体坐标系又是经历大的非线性整体移动和转动这个假设建立的,其基本思想是赋予柔性体一个模态集,采用模态展开法,用模态向量和模态坐标的线性组合来表示弹性位移,通过计算每一时刻物体的弹性位移来描述其变形运动[8]。

柔性体动能可表示为

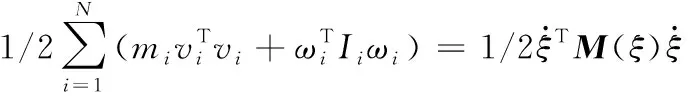
(3)

式(3)中:mi为节点的模态质量;Ii为节点的模态惯量;M(ξ)为质量矩阵;ξ为柔性体广义坐标表达。

柔性体运动微分方程运用拉格朗日乘子法建立如下式:

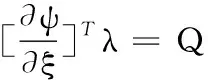
(4)

式(4)中:D、K分别为模态刚性矩阵和模态阻尼矩阵;Kξ、Dξ分别代表物体内部由于弹性变形和阻尼引起的广义力;Q为对应与外力的广义力。

柔性模块中的柔性体是用离散化的若干个单元的有限个节点自由度来表示物体的无限多个自由度。这些单元节点的弹性变形可近似地用少量模态的线性组合来表示。

各部件通过有限元软件ABAQUS进行柔性化。首先将需要柔性化的部件(x_t格式)导入ABAQUS中,对其进行材料属性设置和网格划分,材料属性设置,网格单元采用四面体单元,并确定外部连接节点,完成柔性体的创建。然后将生成的模态中性文件(MNF文件)导入ADAMS中替换原模型中对应的刚性体[13]。对自由状态下的模型进行模态分析,前六阶模态是刚性位移,一般为零,所以提取的模态阶数要大于6,但是模态提取的太多,会给计算带来很大的困难,故也没必要提取的太多,因此提取身管、支架、摇架和托架的15阶模态阶数[7]。图2为身管、支架、摇架及托架柔性化的有限元模型。

图2 各部件柔性化有限元模型

2.4 载荷定义

武器系统工作过程中,弹丸击发时会产生的后坐力,因内弹道过程较为复杂,所以不考虑弹丸在身管内的运动影响,直接利用已知机枪的膛压变化曲线P-t,并将膛底合力添加在与身管连接的行星齿上,替代击发产生的后坐力。由式(5)计算得出弹丸出枪口前的膛底合力变化曲线Fp-t[14]。

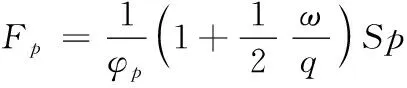
(5)

式(5)中:φp为次要功系数;ω为装药质量;q为弹丸质量;S为弹膛断面积;p为火药气体平均压力,可通过内弹道计算得到。

膛底合力[15]如图3所示。

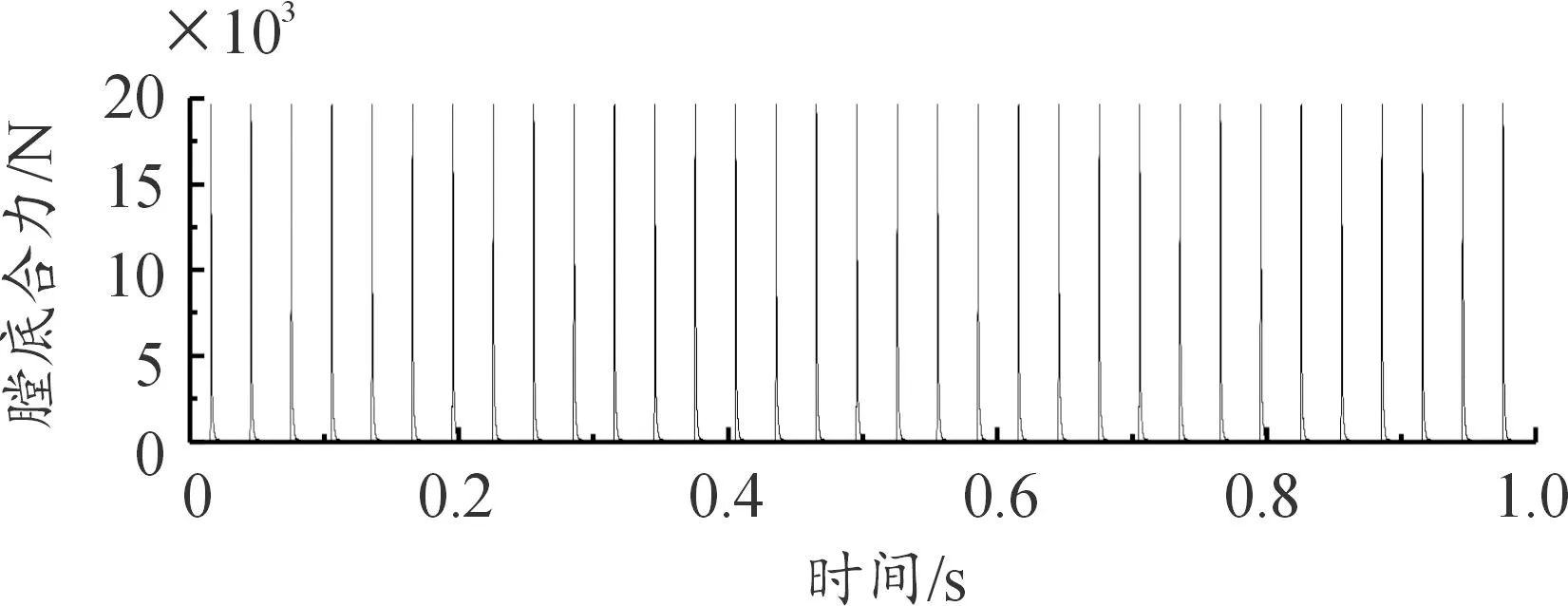
图3 膛底合力图

3 仿真结果分析

通过对5种工况进行仿真计算,其中,工况5为多部件柔性化仿真,与实际射弹过程更相似,但其仿真时长最长。以工况5作为标准,分别与其余工况进行比对,分析了转管机枪射击状态下各仿真工况枪口的振动情况及仿真时长,仿真曲线如图4、图5所示。由图(a)—(h)可知,枪口在各方向为周期性振动,因此以枪口位移的最大值、平均值作为各工况的比对值,枪口响应参数结果如表3所示。表中H1为枪口高低方向位移最大值(上负下正);H2为枪口左右方向位移最大值(右正左负);H′1为枪口高低方向振动位移平均值;H′2为枪口左右方向振动位移平均值(数值正负表示方向)。

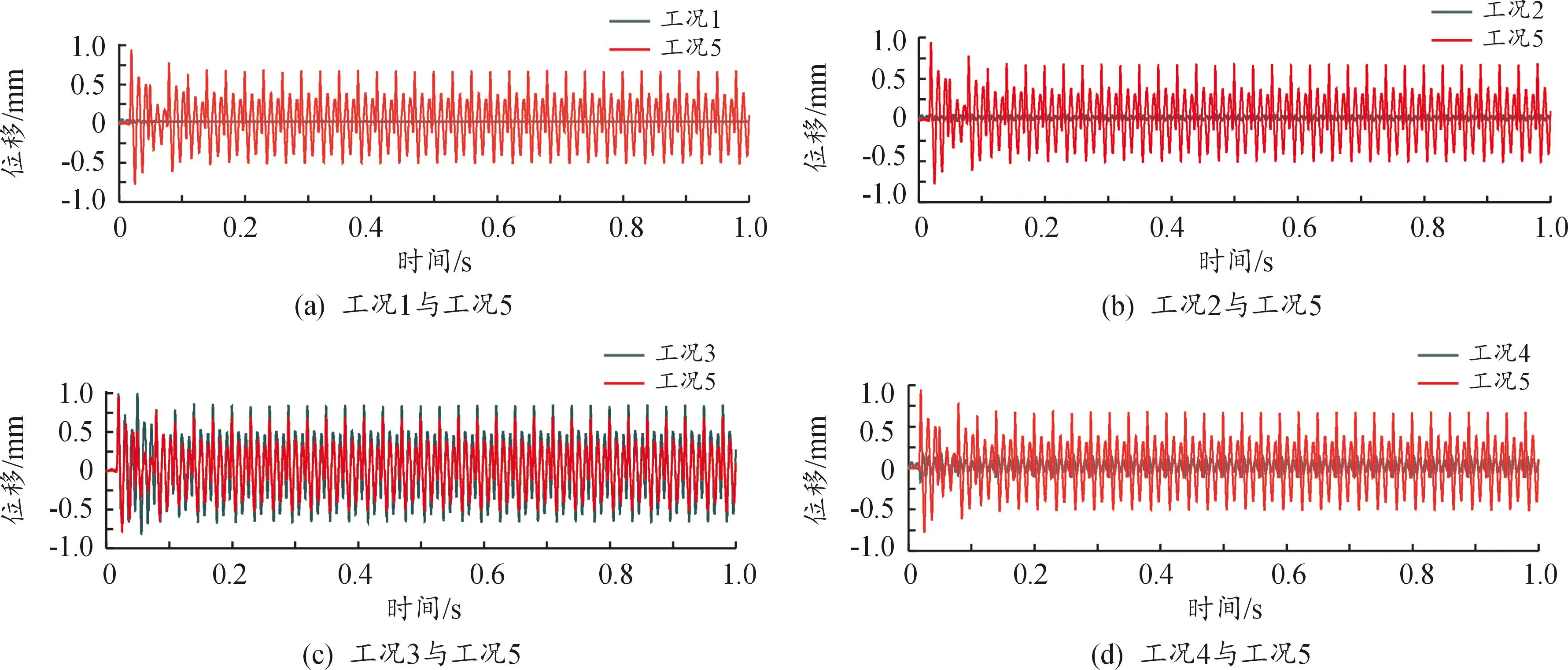
图4 枪口x轴方向(高低方向)位移图

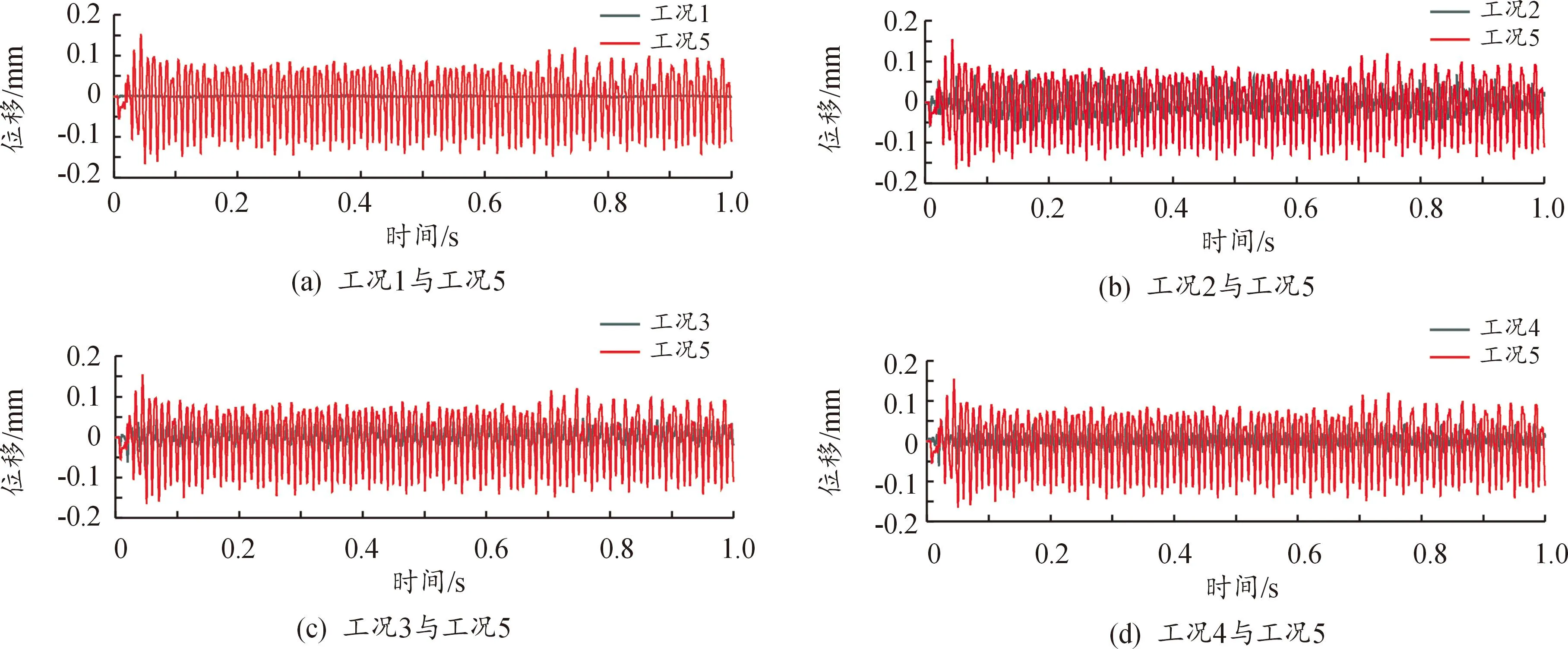
图5 枪口z轴方向(左右方向)位移图

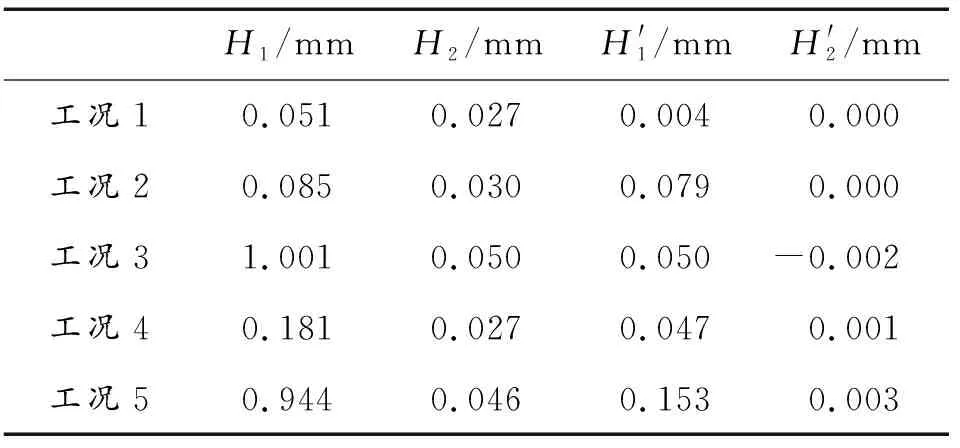
表3 枪口位移响应表

分析表3中各工况枪口位移响应可以得出:在同一工况下,枪口位移在各方向均为周期性振动,高低(x轴)方向枪口位移均大于左右(z轴)方向枪口位移。由工况5枪口位移可知,高低方向枪口位移远大于左右方向枪口位移,因此,忽略枪口左右方向的位移。在高低方向上,工况1—4中,工况3的枪口位移最大,工况1的枪口位移最小,即在射弹过程中,该武器摇架变形对枪口扰动影响最大,依次是托架、支架,架体无柔性体时对枪口扰动影响最小。

图6中h为枪口高低方向位移,枪口与转管机枪支架固定位置之间距离为685 mm,当转管武器进行射击后,各部件在后坐影响下产生弹性变形,枪管会在弹丸燃气高压作用下产生弹性变形,相应地枪口处会与水平方向产生一个夹角θ。枪口角位移θ如式(6)所示。

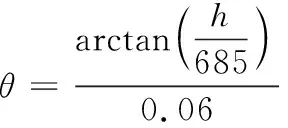
(6)

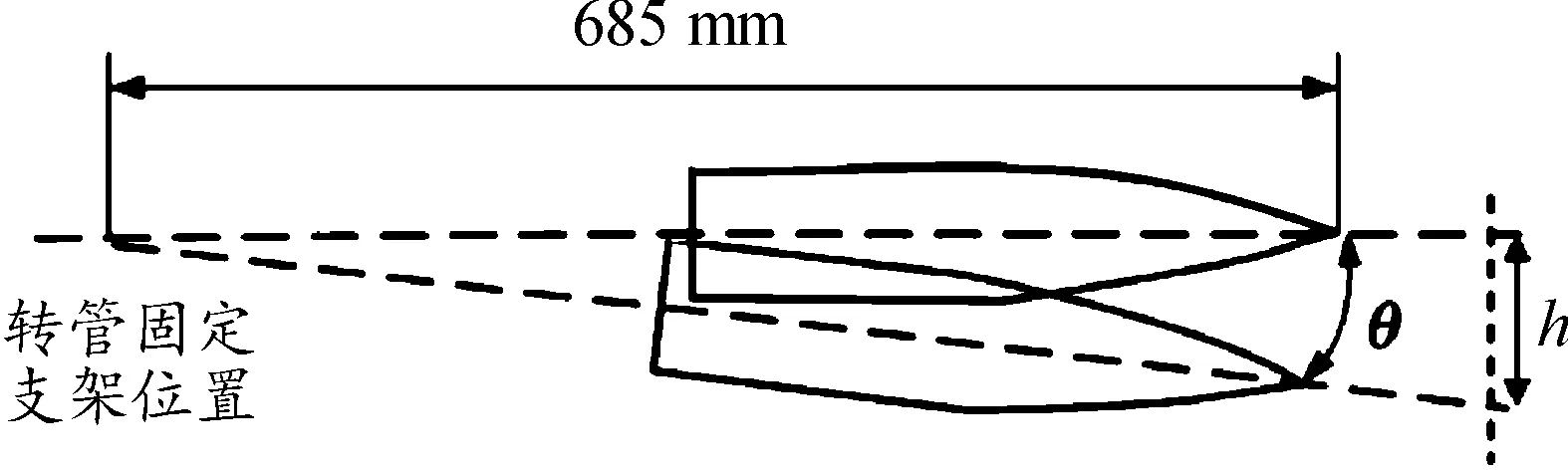
图6 枪口偏移示意图

通过比对各工况在高低方向的枪口位移可知,工况3与工况5在高低方向上枪口位移相近,其余工况对枪口位移的影响较小,说明工况3为该武器系统射弹过程中的主要变形部件。由表3计算得出工况3枪口高低角位移为1.395 mrad,工况5枪口高低角位移为1.316 mrad,其工况3比工况5的枪口高低角位移大6%,由此可知武器系统的单一变形部件作为柔性体可能比多个部件同时作为柔性体时引起的枪口位移更大。

4 结论

通过分析得出以下结论:

1) 该武器在射弹过程中摇架变形对枪口扰动的影响最大,枪口最大位移为1.001 mm,依次是托架、支架、身管,身管作为柔性体时对枪口扰动影响最小,枪口最大位移为0.051 mm。

2) 该武器仅摇架作为柔性体时引起的枪口位移比摇架、托架、支架和身管同时作为柔性体时引起的枪口高低角位移大6%,说明多个部件同时柔性化会降低该武器的枪口扰动影响。

3) 通过分析得出该武器各部件在射弹过程中变形引起的枪口扰动程度,可以为该武器后续的结构优化提供理论基础。

本文中只对该武器在射弹过程中各部件的变形进行了分析,但各装配件之间的间隙也对枪口振动的有较大影响;而且弹头在枪管内运动本身就存在扰动,后续将分析弹丸在枪管内的变形及间隙对枪口影响进行研究。