转化糖浆中蔗糖饱和浓度的推算

谭文兴，曾练强，钟志才，吴兆鹏，郑剑辉，杨虎泉，梅 二，李朝明*

(1 广东省科学院生物与医学工程研究所，广东广州 510316；2 云南西双版纳英茂糖业有限公司，云南景洪 666100；3云南西双版纳英茂糖业有限公司景真糖厂，云南勐海 666300)

0 前言

蔗糖转化糖浆[1]是用稀酸或酶对蔗糖水溶液作用后所得的蔗糖、葡萄糖和果糖的混合物。根据转化程度不同，蔗糖含量不等。由于转化糖的存在，相同温度下蔗糖在水中的溶解度会变小。生产过程水溶解蔗糖时一般要加热升温，此时蔗糖溶解度增加，为确保生产的蔗糖转化糖浆产品在降温后或保存时蔗糖不会结晶，必须知道在转化糖存在时蔗糖在不同温度下水中的溶解度。但目前没有现成的任意温度、任意转化糖浓度下的蔗糖溶解度[2]表，也没有简明的推算方法。

本文根据现有的不完整数据表，通过Excel 软件，结合图表，对不同温度下蔗糖饱和浓度时总糖浓度-转化糖浓度坐标点分布进行最小二乘法曲线拟合[3]，并进行外推，得到蔗糖饱和浓度时总糖浓度-转化糖浓度二次方程。再分别对上述不同温度下的二次方程各系数-温度坐标点分布进行最小二乘法曲线拟合，并进行外推，得到各系数-温度的二次方程。由此可推算得到任意温度、任意转化糖浓度下的蔗糖饱和浓度时的总糖浓度。

1 推算方法

1.1 推算依据

《甘蔗制糖工业手册》(上册)[4]表5-1-5“转化糖存在下蔗糖在水中的溶解度”给出了温度40～65℃下，1.00、1.10、1.20、1.40、1.60、1.80、2.00、2.20、2.40、2.60、2.80 g 转化糖/g 水的蔗糖溶解度。

1.2 数据转换

为了更直观地反映各温度下转化糖含量与蔗糖饱和时总糖(转化糖+蔗糖)浓度的变化，把《甘蔗制糖工业手册》(上册)表5-1-5 在Excel 表格中，用以下公式进行转换：

转化糖含量(g/g 糖浆)=转化糖量/(转化糖量+蔗糖量+水量)

总糖含量(g/g 糖浆)=(转化糖量+蔗糖量)/(转化糖量+蔗糖量+水量)

通过计算得到40～65℃下转化糖含量与蔗糖饱和时总糖浓度的关系，结果见表1。

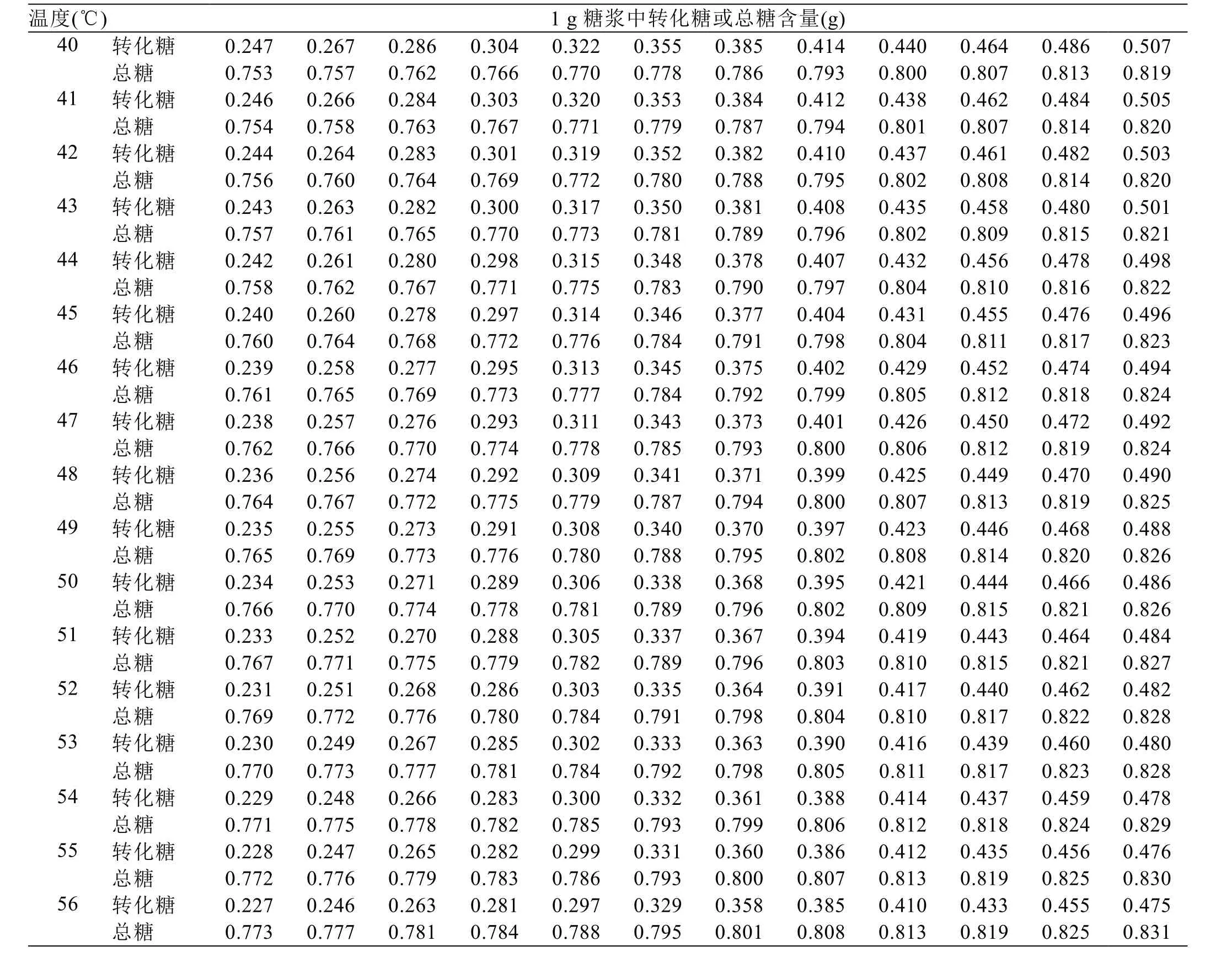
表1 转化糖含量与蔗糖饱和时总糖浓度的关系

1.3 曲线拟合

结果如图1 所示，在Excel 表格中对表1 进行操作，先选择40℃的数据，采用“插入”“散点图”，再“添加趋势线”，并设定为二次曲线，即完成了40℃时转化糖含量为横坐标，蔗糖饱和时总糖含量为纵坐标的曲线拟合；依次在上图中增加41、42、∙∙∙∙∙∙65℃的曲线拟合，得到一系列的曲线拟合图。

图1 蔗糖饱和时转化糖含量与总糖含量关系的二次拟合曲线图

每条曲线代表一个温度下转化糖含量与总糖含量关系的二次曲线y=ax2+bx+c(其中y为总糖浓度，a、b、c为对应的拟合曲线系数，x为转化糖浓度)，同时可得到各曲线的系数，结果见表2。

表2 对应各温度下转化糖含量与总糖含量关系的二次曲线系数

在Excel 表格中，以温度为横坐标，分别以系数a、b、c为纵坐标，得到3 个系列的散点图。再分别对3 个系列进行数据拟合，同样得到二次曲线拟合图，并且得到拟合曲线的方程如下，其中t为温度。

即a1=-0.000004 ，a2=0.0014 ，a3=0.0980 ；b1=0.00001，b2=-0.0028，b3=0.2340；c1=-0.00001，c2=0.0030，c3=0.6086。

1.4 计算公式

把上述(1)(2)(3)式代入公式y=ax2+bx+c中，可得到：

用此公式即可计算任意转化糖浓度和任意温度下蔗糖饱和时的总糖浓度。

2 验算

依上述1.4 推导的公式，对《甘蔗制糖工业手册》(上册)给出的关于蔗糖溶解度的数据进行验算，结果见表3。

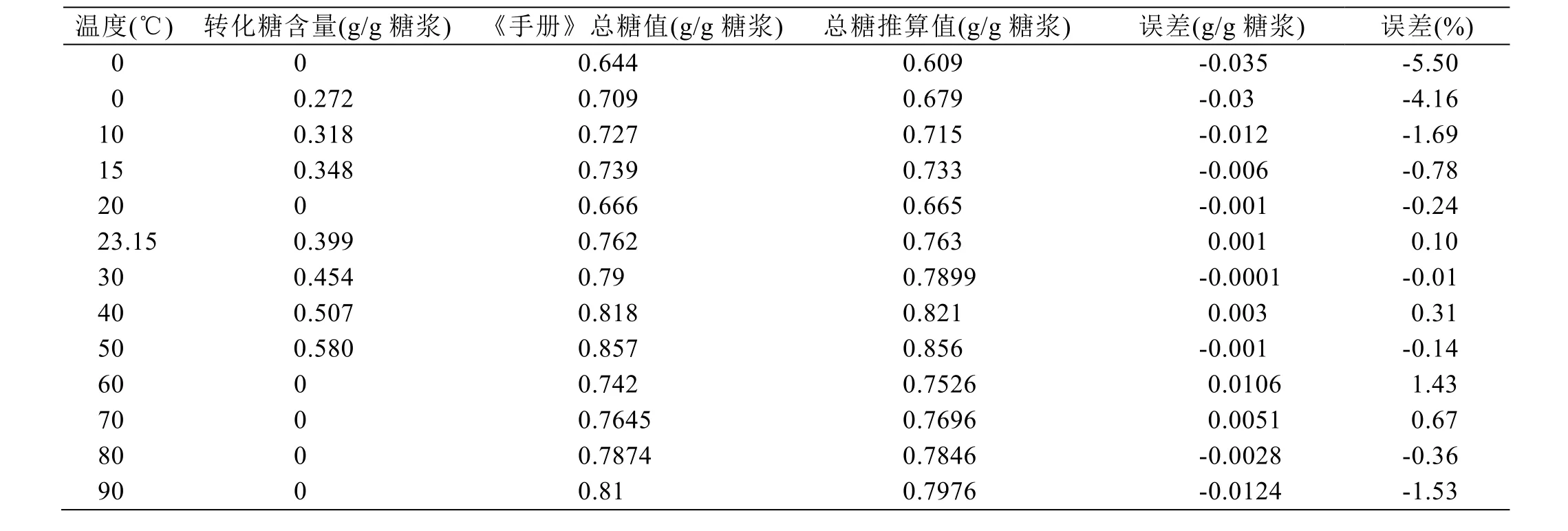
表3 验算结果(一)

依上述1.4 推导的公式，对表1 的部分数据进行验算，结果见表4。

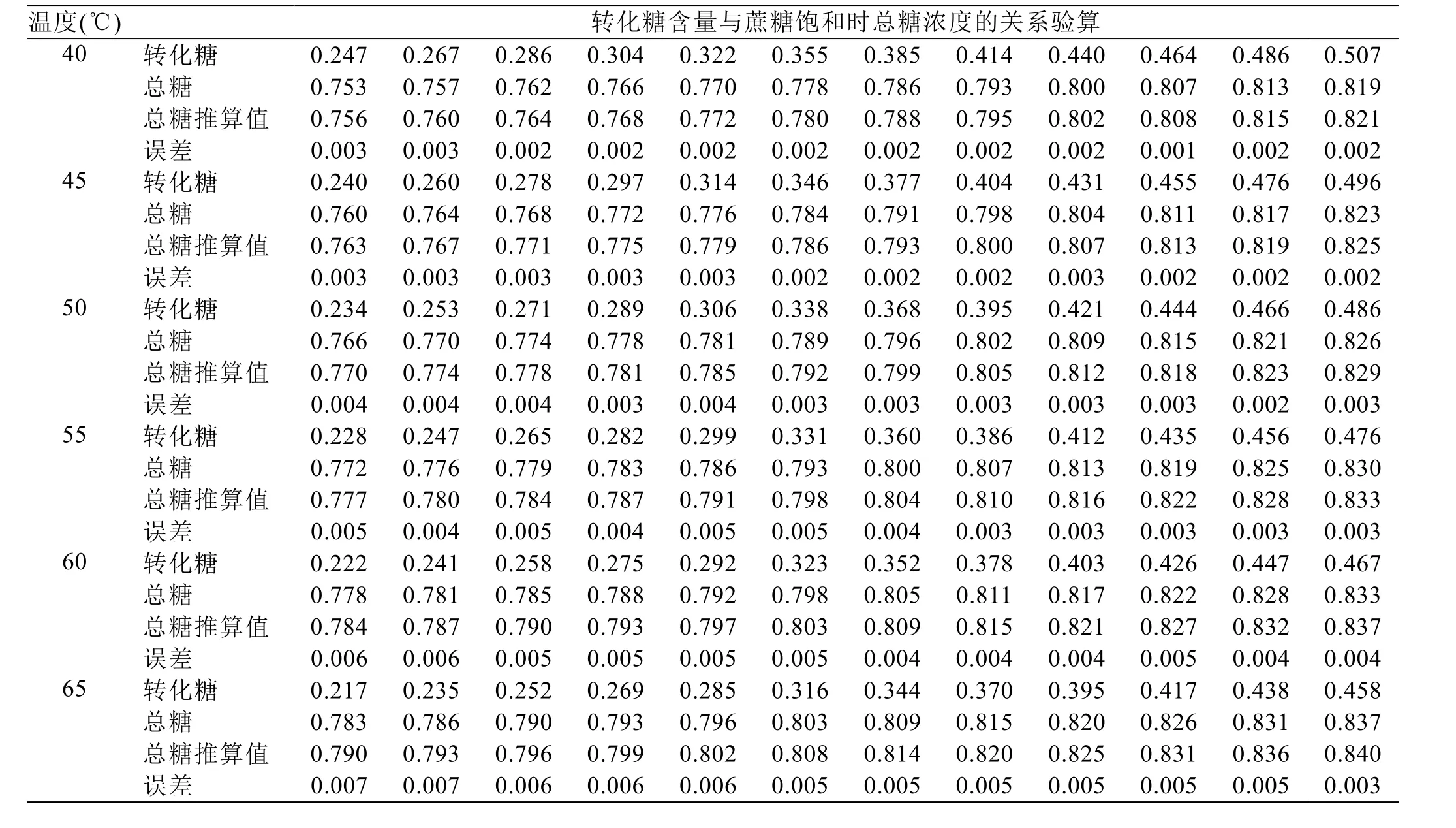
表4 验算结果(二) 单位：g/g 糖浆

3 结果与讨论

3.1 拟合曲线

在对表1 进行曲线拟合时，相关系数R2均大于0.9999，说明40～65℃各温度下蔗糖饱和时总糖浓度能用转化糖浓度的二次曲线完美拟合。

但对表2 各系数对进行曲线拟合时，a、b、c三条曲线的相关系数R2分别为0.5551、0.8752、0.9975，相关系数偏离1 较远的主要原因可能有以下2 方面：

(1)原数据表5-1-5 的数据均为3 位有效数位，转换后也保留3 位有效数位，4 舍5 入的方式可能造成误差的传递，放大了误差。以40℃的数据为例，表5-1-5 的原数据见表5。转换为本文的数据后，结果见表6。

表5 40℃转化糖含量与饱和蔗糖浓度的关系

表6 40℃转化糖含量与蔗糖饱和时总糖浓度的关系

此时，拟合曲线为y=0.138x2+0.1488x+0.7079。

如果把原数据饱和蔗糖的2.02 合理地修改为2.025，则转换后表中总糖变为0.758，而拟合曲线变为y=0.1424x2+0.1451x+0.7087，与原式有明显差别。

(2)由于c是常数，代表了总糖的主要组成部分，而b、a分别为一级纠偏和二级纠编系数，因此，c的拟合曲线系数为0.9975，说明本文推算的结果总体应该不会差太多；纠偏系数的误差可能是因为数据只有40～65℃的部分，偏离这一温度范围的推算值可能误差稍大些。

3.2 验算结果

从表3 和表4 可以看出，用本文推导的公式推算的总糖结果与《甘蔗制糖工业手册》给出的结果相比，误差有正有负，最大的为-0.0035(相对误差-5.50%)，出现在0℃的纯蔗糖溶液；而大多数情况下，误差小于1%。只有在极端温度条件下(如大于90℃或小于10℃)，本文推导的公式推算的结果才会与实际情况偏差较大，其他情况下推算的结果可作为生产应用时参考。

4 结论

本文从《甘蔗制糖工业手册》(上册)表5-1-5(40～65℃转化糖存在下蔗糖在水中的溶解度)数据出发，通过最小二乘法拟合曲线，得知同一温度下蔗糖饱和时的总糖浓度是转化糖浓度的二次函数，即y=ax2+bx+c；进一步分析得知a、b、c分别是温度t的二次函数，即a=a1t2+a2t+a3、b=b1t2+b2t+b3、c=c1t2+c2t+c3，并求解得到a1、a2、a3，b1、b2、b3，c1、c2、c3。

用此公式计算任意转化糖浓度和任意温度下蔗糖饱和时的总糖浓度，其误差在生产应用许可范围。