基于多面体和靶标的转台运动精度测量方法研究

林修文,罗道江,冯刚英

(中国电子科技集团有限公司第十研究所,四川 成都 610036)

0 引言

伺服转台可为环扫天线提供精确的方位和速率等输入信号,通过转台旋转带动环扫天线实现天线波束指向有规律的改变,转台的运动精度直接影响环扫天线指向精度。随着空天电子装备的迅速发展,天线性能指标要求不断提高,对天线转台运动精度的测量成了必需的工作。

目前,国内外对于精密转台运动精度测量尚未形成统一的标准,也没有成熟的商用设备[1]。通常根据转台结构特点、使用性能要求以及具备的测量仪器情况,设计并搭建测量平台[2]。由于测量环境和测量仪器的限制,大多采用间接测量的方法,再进行推导计算得到结果,难以保证测试精度的可信性[3]。本文结合多面体法和靶标法直接对天线转台运动精度进行测量,减少了过程转换误差,并对测量方法展开了误差分析。

1 运动精度测量方案

1.1 测量装置的设计

本测量方法中用到的仪器主要有电子经纬仪、正多面棱体、平面度检测仪、千分表。

测量前,设备及仪器按如图1所示放置,其中电子经纬仪通过转接夹具固定在输出主轴的安装法兰上。装配过程中将千分表通过磁力吸附固定在转台上,测量电子经纬仪和主轴的同轴度,配合调整转接夹具的安装位置使同轴度达到千分表的最小分度值。然后在距离电子经纬仪h处放置平面靶标,转动电子经纬仪使得观测镜和靶标中心重合并置零电子经纬仪的读数。最后将正多面棱体装配在与旋转变压器轴回转中心同轴的位置上,平面度检测仪放置在正多面棱体附近,调整平面度检测仪观测镜中的光管与正多面棱镜中任一镜面刻线重合[4]。此时测量仪器的设置作为测量初始状态。

图1 多面体法和靶标法组合的测量系统

1.2 测量原理及过程

将电机输入轴顺时针转动,带动正多面棱镜转动,使平面度检测仪观测镜中的光管与正多面棱镜中相邻镜面刻线重合,此时旋转变压器轴转动角度为α。将电子经纬仪逆时针旋转,使观测镜和靶标中心重合,记录此时主轴转动角度的读数β1,可以得到旋转变压器轴位置在α时,运动精度误差值φ1=β1-α[6]。

然后通过同样的方法将旋转变压器轴再次转动α,操作电子经纬仪使观测镜和靶标中心重合,记录第二次主轴转动角度的读数β2,可以得到旋转变压器轴位置在2α时,运动精度误差值φ2=β2-2α。

对于其他位置,都通过上述方法依次进行测量和计算,可以得到n-1组正向误差值数据φ1,φ2,φ3,…,φn-1,其中φn=βn-n×α。

2 不确定度分析

本测量方法的不确定度主要来自传动变压器轴和转动主轴两端的测量装置,即多面体法和靶标法测量系统带来的不确定度。

2.1 多面体法不确定度分析

多面体法测量系统中的不确定度来源主要是平面度检测仪精度γ1、多面棱镜的精度γ2及观测误差γ3。其中,观测不确定度主要来自人自身的视觉误差,人眼的分辨力为30″～60″,观测观测镜的放大率为V,可以得到观测不确定度γ3:

(1)

2.2 靶标法不确定度分析

靶标法测量系统中不确定度来源主要有电子经纬仪与输出主轴的偏心误差引起的不确定度和电子经纬仪对靶标过程中引起的不确定度。

电子经纬仪与输出主轴的偏心误差来源于装配过程中使用的千分表的最小分度值。如图2所示,实线圆代表输出主轴,A点为其轴心,虚线代表电子经纬仪,B点为其旋转中心,A点与B点的距离m代表偏心的距离,r代表使用千分表调整安装同轴度时接触点(C点)与旋转中心(B点)的距离,B点到C点的方向代表与靶标对准的方向,直线AC与BC之间的夹角c即是偏心引起的不确定度γ4。

图2 偏心误差来源示意图

由余弦定理,可以通过式(2)得到不确定度γ4:

(2)

由均值不等式原理,通过式(3)得

(3)

电子经纬仪对靶标过程中引起的角度误差来源于仪器误差和观测误差γ5[8]。

仪器误差主要来源设备内部物理特性和加工装配引起的误差,如图3所示,O为观测镜观测点,D为靶标中心,p为仪器测量误差,因此∠DOD′即为仪器误差引起的测量误差γ5。

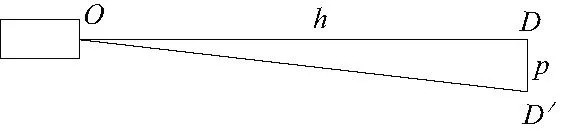
图3 仪器误差引起测量误差示意图

由三角定理,可以通过式(4)得到γ5:

(4)

2.3 运动精度测量方法总不确定度

根据引起运动精度测量方法不确定度的来源,可以得到方法总不确定度γ:

(5)

3 验证与分析

3.1 验证案例

以工程项目中某环扫天线转台作为验证案例,按照本文论述的方法进行运动精度测量,搭建的测量系统如图4所示。

图4 某转台运动精度测量系统

本测量平台采用12面棱体,不确定度γ1=2.9″;平面度检测仪不确定度γ2=1.2″[4];取人眼的分辨力为60″,观测观测镜的放大倍率V为20,通过式(1)可以得到观测不确定度γ3=3″;千分表最小分度值0.001mm, 千分表距离主轴旋转中心距离r为100mm,通过式(2)、式(3)可以得到γ4=2.1″;经纬仪精度p为0.002mm,靶标设置在距离经纬仪5m的地方,通过式(4)可以得到γ5=0.1″。

由式(5)计算可知测量方法的总不确定度γ=5.7″。

对转台正向和反向分别每间隔30°依次进行测量,得到的数据如表1和表2所示。由表1得正向运动精度误差最大值为2′29″;由表2得反向运动精度误差最大值为2′03″。

表1 正向运动精度测试数据

表2 反向运动精度测试数据

3.2 案例分析

本案例以12面棱体作为旋变轴输入基准,按测量步骤读取电子经纬仪数值,得到正向和反向各12组运动精度误差值数据,对测量数据采用极差原理计算可以得到正向运动精度ω=2′29″,反向运动精度ω′=2′03″,满足转台的使用运动精度小于6′的指标要求。

本案例中搭建的运动精度测量系统均采用常规检测仪器,测量系统的总不确定度达到5.7″,满足工程项目中绝大部分的高精度测量需求。

4 结语

本文针对工程实际中环扫天线转台的运动精度测量问题,设计了基于“电子经纬仪+靶标”和“平面度检测仪+正多面棱体”组合搭建的测量系统,实现直接对转台输入端和输出端的角位移测量。相较于间接测量法,本方法可以简化测量数据处理步骤并减少中间推导过程中引入的误差,其结果具有计算方便和精度高的特点。本文详细论述了测量方法的步骤和不确定度的算法,最后采用常规检测仪器按照该方法搭建的运动精度测量平台对工程中某环扫天线转台进行检测。由测量结果可以得出,本测量平台检测误差满足工程项目中的高精度测量要求。