基于认知不确定可靠性的产品功能优化算法研究

钟维宇,戴俨炯,蔡敢为,柳林燕

(1. 空军航空维修技术学院 航空电子设备维修学院,湖南 长沙 410129;2. 广西大学 机械工程学院,广西 南宁 530004; 3. 南京理工大学 机械工程学院,江苏 南京 210094)

0 引言

随着智能制造飞速发展,产品功能趋向多样化、复杂化和专业化,产品设计过程以系统可靠性、功能性、确定性为设计基准,大力倡导模块化、系列化、通用化设计理念,以实现产品多功能及专业性全覆盖。

可靠性作为产品的重要设计属性之一,在不确定因素下产品可靠性的高低直接决定了产品能否高品质、无故障地工作运行。影响可靠度评估的不确定因素太多,且涉及的问题较多。方永锋等[1]将可靠性指标转化为随机可靠性指标,得到区间参数串联、并联的表决系统可靠度计算方法;欧阳惠卿等[2]将串-并联系统和优化后并-串联系统的可靠性进行了推导计算。但以上研究对于不确定可靠度理论与分析方法尚存在不足。

产品设计的方案阶段,以产品的功能分析为主,进行产品的总功能、子功能分解,功能优化设计过程中存在多个复杂的、相互冲突的优化目标,故传统的方法在处理时受到很大的约束。因此,建立不确定可靠性产品功能算法模型,对多个优化目标进行分析求解,寻找最佳的目标方案组合,以实现产品方案设计与功能优化设计并行[3]。

1 认知不确定可靠性方法

产品功能优化分析中不确定可靠性主要分为两类:随机不确定性、认知不确定性。认知不确定可靠性即通过概率理论反映产品功能优化过程中认知不确定性的主观因素及客观因素。

认知不确定方法将产品总功能、子功能、细分功能等分别转化为认知集合,形成由可信度和似真度组成的认知不确定概率区间。

认知集合定义为影响产品功能的一切不确定性因素的集合,其子元素两两互斥通常用Λ表示。

(1)

式中:u1为认知集合Λ的子元素;n是子元素个数,i=1,2,3,…,n。

设计者对不同功能子集进行分析阐述,确保认知不确定性的真实、可靠、牢固。此过程等同于对认知集合进行积分运算,又称为基本可信度分配,需满足以下公式:

(2)

式中:m为基本可信度分配函数;x为认知集合所对应的2Λ的任意子集;m(x)为事件x的可信概率。

基本可信度分配反映了命题x为真实的信任程度。目前,针对基本可信度分配函数,常用的构型有贝叶斯型构型、概率型构型及辅助型构型,任何子集在区间范围内,可信度概率位于[0,1]区间内。

产品不同功能需求来源及实现方式不同,处理不确定信息的多元化程度,合成认知集合中命题的总信任程度至关重要。目前,常见的合成法则有Dempster、Yager、Inagaki等[4-6]。

认知集合Λ中子集G,对于可信度和似真度可以采用区间集合[B(G),P(G)],两个指标集合组成Λ的信任程度:

(3)

(4)

式中:B(G)是子集命题G中的命题x完全包含于认知集合G基本可信度之和;P(G)是子集命题G中的命题x与子集命题G交集不为空的基本可信度之和。当P(G)与B(G)所形成的区间敞口越大,说明信息的不确定性加大。真实的可靠度一定介于可信度和似真度之间,B(G)和P(G)满足以下公式:

(5)

Bel(G1∪G2)≥B(G1)+Bel(G2)-B(G1∩G2)

(6)

P(G1∩G2)≤P(G1)+P(G2)-P(G1∩G2)

(7)

2 认知不确定可靠性算法模型

基于认知不确定可靠性产品功能设计优化是一个繁复和庞大的计算过程,在给定设计输入不确定性的情况下,设计者无法判别功能需求不确定性等因素,根据不同需求认知不确定性基本可信度,考虑实际产品设计过程中时效性,低值不确定性功能的问题可以选择近似替代初始模型并通过样本策略构建高效的模型[3,5]。

综合考虑多种不确定因素条件下选定目标可靠度,寻找最优不确定设计变量的表达式:

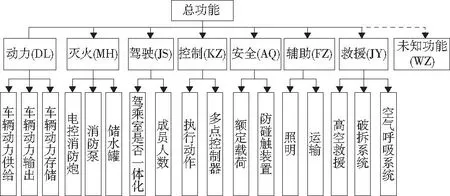
F={g:g(Xi)

(8)

(存在:vart、x;最小边界minf(t,x);

s.t. Prob(Gj(t,x)≥0)≥1-Φ(-βj);

tb≤t≤tp;j=1,2,…,p

式中:g0为目标产品可靠性失效值;Xi为相互独立的不确定性变量识别集合;F为失效域;x是不确定功能变量,即认知集合所对应的2Λ的任意子集。

认知不确定可靠性模型采取区间集合[B,P],集合中左边界(下限)为B和右边界(上限)为P,β是约束目标参考可靠度;t=[t1,t2…,tn]T是产品设计变量向量;tb表示其下限值,tp表示其上限值。

概率约束是计算极限状态函数在随机变量输入积分区域gi(x)<0的概率。考虑到极限状态函数与联合概率密度函数求解的复杂性,工程计算一般采用空间转换再积分的方法进行简化。首先,设均值和方差分别为ux和σx,通过标准化转换后的现有空间成为u空间,则有

(9)

相应的u空间可靠性积分公式展示为

(10)

(11)

相应得出u空间中独立变量的联合概率密度函数可表示为

(12)

采用功能度量法进行逆可靠性分析,可靠度指标法的目标函数及约束相互对偶,功能度量法的数学模型可表示为:

(13)

为了找到可靠性指标β的逆可靠性分析来找到功能度量法,通过分析其灵敏性,通过获取设计灵敏度,定义如下:

(14)

从而可得u*对设计变量的灵敏度用微分式子来表达如下:

(15)

(16)

(17)

在X空间的功能评估变换矩阵T和Hessian矩阵H,如式(18)所示;X空间中功能的灵敏度以矩阵形式表示,如式(19)所示。可以获得在u空间中功能灵敏度相对于设计变量的灵敏度,从而优化获取最优解组合。

(18)

(19)

上述认知不确定可靠性数学模型作为真实系统行为决策的近似表达,不确定性功能数据来源于现实需求、理论假设和经验相关性。该方法将不确定性功能变量转换成概率变量,构建等效的概率可靠性设计优化模型,每个不确定变量在其平均值附近分配概率分布,然后通过数学模型将此不确定性传播到输出,通过计算机迭代求解,使用数值技术来产生数学模型的近似解。上述模型仅限于求解连续方程的离散近似解,执行最优解筛选Λ={uS},S为优选功能[7]。

3 认知不确定可靠性算法计算流程

根据认知可靠性模型,构建认知可靠性计算程序,其计算步骤程序既严谨又可调节,需根据实际产品的复杂程度和真实需求,对相关计算步骤进行适当裁剪[8-9],如图1所示。

图1 认知不确定可靠性计算流程

步骤一:总体功能分析

产品总体功能分析主要包含总体系统定义及产品功能原理初步分析,转变为认知集合。总体系统定义为产品功能信息梳理、归纳及定义,包括产品的主要功能、产品的构成等。根据总体功能分析的结果,梳理出各功能对应的确定性要求。每个功能对应的需求可能是一对一或一对多。

步骤二:子功能概率化及可信度分配

产品子功能概率化包括功能原理细化及关键特征,转变为识别集合。功能原理细化采用图表分析法,绘制产品功能框图,明确完成子功能的各组件可能的方案。针对识别集合中不确定因素进行变量化处理,采用Dempster合成法则,形成可信度分配。若可信度分配中可信度与似真度敞口过大,代表信息不确定性过强,返回总体功能分析层,进行优化完善;若可信度分配中可信度与似真度敞口合适,代表信息不确定性合适。

步骤三:最优不确定设计变量

选择初始样本点,将认知集合信任度中[B,P]、可靠性失效值分别作为可靠性失效方程边界及约束。可靠性失效值明确主要功能丧失时各相关的功能性能参数边界值,在分析时应当注明使用约束参数的取值。可靠性失效值一般通过查询产品相关领域产品设计或验收规范,结合产品设计功能需求,在适当加严后得到产品失效值分析方法;接下来,输入认知不确定可靠性计算最优解模型,进行函数空间变化,变换后形成联合概率模型,便于提前进行相应功能调整。

步骤四:迭代计算获取优选功能组合

采用功能度量法,获取极限状态函数,分析设计灵敏度,计算出可靠性指标,满足收敛标准,即可获得优选功能组合,以确保此过程中方法的准确性。

4 算例

本文以举高消防车为例进行产品功能优化分析。举高消防车功能复杂、作业模式及作战效率要求高。应解决产品在设计初期遇到的不确定因素干扰,从而提升产品可靠性。

4.1 举高消防车总体功能分解

总功能分解是多种技术系统的综合分析,设计者初期应直观地分辨产品具体功能、区分不同功能种类,从而形成完整的技术方案。举高消防车功能需求主要包含性能、环境、可靠性等方面,举高消防车总功能具体按动力、灭火、驾驶、控制、安全、辅助、救援及未知功能(可扩展)来描述[10],如图2所示。

图2 举高消防车总功能分解图

将举高消防车总功能定义为认知集合Λ,动力功能(DL)包含车辆动力供给u1、车辆动力输出u2,依次类推,则认知集合Λ={u1,u2,u3,…,u18}。

4.2 举高消防车子功能概率化及可信度分配

举高消防车认知集合中子元素u1,u2,u3,…,u18(即不同功能)来源于N个不同的信息源头,包含同类产品技术水平、技术数据、技术方案、试验数据等,这些信息中有确定性、不确定性、真实、虚假等类别。以举高消防车灭火功能为例进行子功能分解如表1所示。

表1 举高消防车灭火功能(MH)子功能

灭火功能(MH)模块子集分别为u4、u5、u6,u4中包含以下几种子功能:水B1、泡沫灭火剂B2、干粉灭火剂B3、卤代烷灭火剂B4及其他未知信息B5,故其识别集合为{B1,B2,B3,B4,B5}。同理,可以得出u5、u6的识别集合。

识别集合中子元素之间矛盾较小,采用Dempster合成法则,根据式(2)得到识别集合基本可信度分配m(u4)、m(u5)、m(u6)。

根据式(3)、式(4),选用标准正态分布进行随机变量化,形成认知集合基本可信度分配m(MH)。在已知可信度分配的基础上,对于采用可信度和似真度组成的区间[B(G),P(G)]产生可信度和似真度如表2所示,信息不确定性敞口区间为[0.136 4,0.591 9]。

表2 举高消防车功能可信度及似真度区间

根据不同功能模块的可信度和似真度、设计经验数据及企业参数来源,最终确定Λ的信任程度为0.263 2。

4.3 举高消防车认知可靠性优选功能组合

以认知不确定可靠性计算流程(图1)为基础,确定最优不确定变量设计(即初始样本点)方案,可靠性失效值分别作为可靠性失效方程边界及约束,结合联合概率函数及极限状态函数,进行函数空间变化,采用功能度量法,分析设计灵敏度,计算出可靠性指标,满足收敛标准,即可获得优选功能组合。

计算过程中采用SQL Server数据库系统,满足大量计算数据处理、数据库管理模块及企业级数据开发要求,系统开发主要采用Visual Studio(VS)。优选功能组合计算流程代码如图3所示。

图3 优选功能组合计算流程代码

根据客户对产品功能、性能的要求可以进行举高消防车优选功能重组。比如根据客户对驾驶室的乘员人数要求,改变驾驶室的人员参数,且系统各功能之间具有关联性、系列化、互换性[8-10]。功能度量法收敛策略如图4所示,获得城市主战消防车最优功能模块划分结果如表3所示。举高消防车优选功能分为A-D 4种组合,不同组合对应相应的灵敏度数值,A组合的灵敏度值最小,故优先选择A组合进行优化设计。

表3 举高消防车优选功能组合

图4 功能度量法收敛策略

5 结语

本文构建基于认知不确定可靠性产品功能优化算法流程,根据总体功能分析、子功能概率化、可信度分配、最优不确定设计变量及迭代计算获取优选功能组合等步骤,计算出可靠性指标,针对目标多组解决方案,求解出指定概率满足一组约束的最优解。举高消防车的研发是一个具体而复杂的过程,其中包含确定性功能需求、不确定性功能需求及未知功能需求。基于认知不确定可靠性优化模型,以举高消防车为例,进行需求分析及功能分解,建立认知集合,代入认知不确定可靠性算法流程,获取满足设计需求最优功能解,对增强企业新产品开发能力及核心竞争力、提高产品设计可靠性、避免大量冗余工作具有重要的意义。