金刚石颗粒体积分数与刺碰概率和防刺性能的关系探讨

王天增 于伟东 周 胜

1.东华大学 a.纺织面料技术教育部重点实验室,b.纺织学院,上海 201620;2.扬州市职业大学 纺织服装学院,江苏 扬州 225009

自冷兵器时代就开始的防刺装备[1-3]经过长期的研究积累和发展,防刺穿戴产品在轻质、柔软方面[4-5]及防刺功效的有效保持方面[6-7]均得以实现。近年来,较多的研究主要集中于复合树脂片与基布结合形成的半硬质防刺服材料方面[8-12],尤其是金刚石颗粒复合树脂片与高性能织物结合的防刺服材料的研制与表征方面[13]16。无机颗粒增硬的复合树脂片具有轻质、高效防刺的特点[14-15],可作为反恐防暴救援人员穿着用防护服的核心材料。在不考虑复合树脂片与片之间缝隙所产生的穿透率[10]14,仅考虑复合树脂片本身防刺功效时,影响复合树脂片防刺性能的关键在于复合树脂片中无机颗粒的均布密度和体积分数,因为这决定了刀具刺入复合树脂片后与无机颗粒的刺碰概率[13]38。

基于此,本文将金刚石颗粒均匀填充于树脂结构中,探讨该结构下刀具与金刚石颗粒的刺碰概率,并通过复合树脂片的防刺试验,验证均布填充结构下金刚石颗粒体积分数与防刺功效的关系。研究旨在为无机颗粒复合树脂片的增硬、增强和高效防刺提供可靠的数据与工艺设计参数。

1 试验部分

1.1 试验材料

粒径为300 μm(50目)的金刚石颗粒,购自郑州斯迈特实业有限公司;型号为PAA-102的聚酰胺酸(PAA)溶液,固含量为18%,购自常州福润特塑胶新材料有限公司,PAA溶液经梯度升温后,可形成链接或交联并固化成聚酰亚胺(PI)。

1.2 复合树脂片的制备

将金刚石颗粒于丙酮溶液中浸没洗涤,并超声振荡约10 min后,采用鼓风干燥箱对其进行干燥。取适量的PAA溶液在60 ℃下加热5 min,以降低其黏度。取一定质量的PAA溶液与金刚石颗粒,分层铺叠,再经加热固化制备金刚石颗粒/PI复合树脂片(后文简称“复合树脂片”),制备流程如图1所示。

图1 复合树脂片的制备流程

1.3 复合树脂片性能测试

1.3.1 外观形貌观测

观测复合树脂片的断口形貌、表观形貌以及金刚石颗粒在复合树脂片中的分布情况,并在此基础上分析复合树脂片的防刺性能。

1.3.2 防刺性能测试

使用自制的摆锤式织物防刺、割、砍功能组合测量仪,测试复合树脂片的防刺性能。按照GA 68—2019标准[16]对织物或复合树脂片进行测试,设定刺入能量为24 J。

2 复合树脂片防刺性能的理论表达与试验验证

2.1 金刚石颗粒体积分数与刺碰概率的关系

陈立富等[13]76和杨超[17]49通过试验发现,人造金刚石颗粒/PI复合树脂片抵御刀具的刺入主要依靠刀具与金刚石颗粒的刺碰。基于此,研究者提出了复合树脂片抵御刀具刺入的碰撞阻挡钝化防刺机制和反向切割粗糙化机制。刀具与金刚石颗粒的刺碰主要受金刚石颗粒体积分数(fV)、质量分数(fm)和截面积分数(fA)的影响。

2.1.1 金刚石颗粒体积分数与粒径的关系

在复合树脂片中,金刚石颗粒的体积分数影响刀具与金刚石颗粒的刺碰(击中)概率(PS),进而影响复合树脂片的防刺冲击强力(F)。以金刚石颗粒均匀分布的复合树脂片为例进行计算。

(1)

VP总=n×V0P

(2)

(3)

式中:V0P为单个金刚石颗粒的体积;de为金刚石颗粒的粒径,将金刚石颗粒等效为圆球粒;VP总为树脂片中全部金刚石颗粒的体积;n为复合树脂片中金刚石颗粒的数量;VR总为树脂的体积;V总为树脂片的体积,V总=VP总+VR总;V0为复合树脂片中基本单元的体积;树脂片平面可视为规则的长方形,a0和b0为其边长,δ0为树脂片的厚度,则V总=a0b0δ0。

因为金刚石颗粒的粒径为微米级,所以当金刚石颗粒的密度一定且分布均匀时,可视ΔV为定值,则由式(3)可知,fV与de3正相关。

对于颗粒均匀分布的单层树脂片,其基本单元中单个金刚石颗粒体积分数(f0V)的计算式如式(4)所示。

(4)

当复合树脂片中的金刚石颗粒密集排列,并且树脂片的厚度薄到等于颗粒等效粒径de的理想状态时,金刚石颗粒的体积分数等同于树脂片基本单元中单个颗粒的体积分数f0V,此时的f0V=52.36%,达最大填充体积分数。

2.1.2 金刚石颗粒的截面积分数与刺碰概率的关系

单晶体是按其晶胞的形态向外辐射生长的,尤其是在晶粒尺度较小时。同时,结合杨超[17]11采用扫描电子显微镜对不同粒径金刚石颗粒进行观测的结果,可证实金刚石颗粒的外形与其晶胞的形态基本一致,即基本上是由正方形面和正六边形面构成的正十四面体。对该正十四面体进行3D建模,模型包括8个正六边形面和6个正方形面,得金刚石颗粒各个方向的视图如图2所示。该正十四面体中2种形态平面(正六边形面和正方形面)的边长(a)相等。

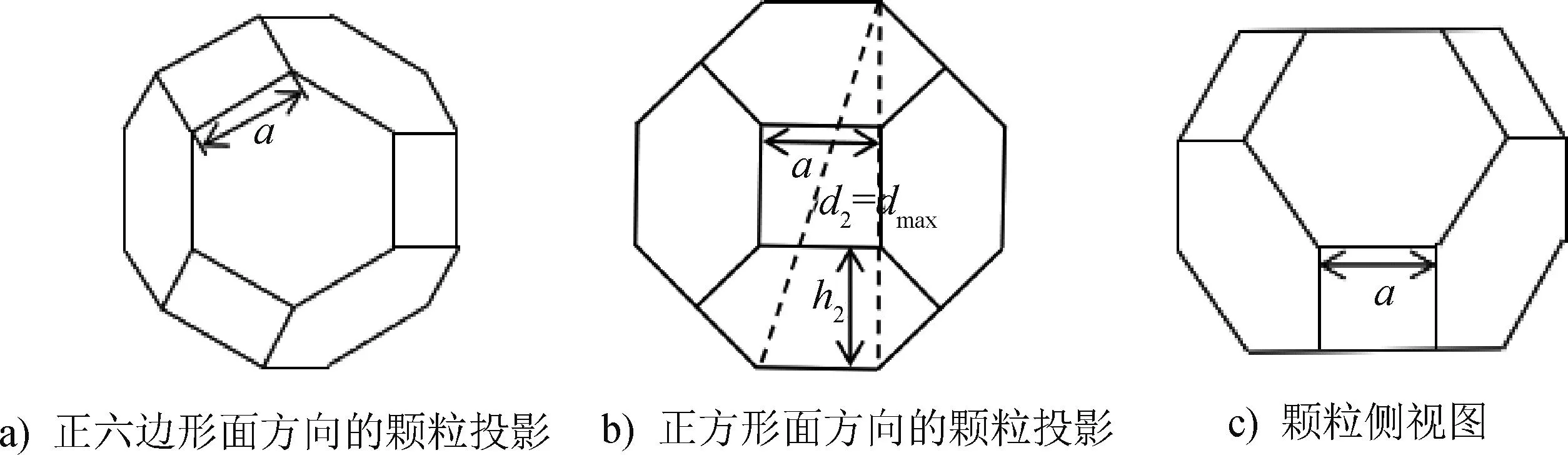
图2 金刚石颗粒各个方向的视图

设正六边形面、正方形面在上且位于水平面时,金刚石颗粒体的2种投影面积分别为A01和A02。同时设:1)颗粒体的正六边形面在上时的正六边形间夹角为γ,正六边形面与正方形面间的夹角为β1;2)颗粒体的正方形面在上时的正方形面与正六边形面间的夹角为β2。取A01和A02中的大者作为最大投影面积A0 max的计算依据;以A01和A02的外接圆直径dmax为方盒边长的计算依据。

颗粒正六边形面在上的颗粒投影面积A01与正方形面在上的颗粒投影面积A02的计算式如式(5)和式(6)所示。

A01=A正六边形+3A侧六边形+3A侧长方形

(5)

A02=A正方形+4A′侧六边形

(6)

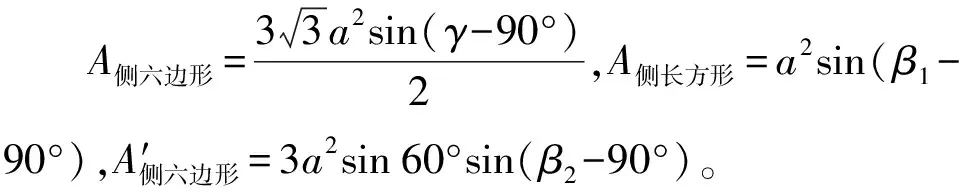
测量金刚石颗粒3D模型中的参数γ、β1和β2可得,γ=109.47°,β1=β2=125.26°。将其代入式(5)和式(6)中,结果发现A02>A01,据此,选择图2b)作为相对最大投影面积A02的计算依据:

A02=a2+12a2sin60°sin(β2-90°)

(7)

(8)

(9)

式中:h2为颗粒正方形面在上的侧边六边形面的高,h2=2asin60°sin(β2-90°)。

按A02投影面积排列时,理论上是最紧密的堆砌形式,故金刚石颗粒投影的面积和体积分数达最大,分别为理论面积分数fAmax和理论体积分数fVmax。此时的刺碰概率(PS)亦与理论刺碰概率(PSmax)趋于同步,并且其值为常数π/4,即

(10)

按A02投影面积的外接圆面积排列,是金刚石颗粒在树脂黏稠液中随机分布的最紧密的堆砌形式,故金刚石颗粒的外接圆面积和体积分数达到实际可能的最大,分别为最大截面积分数fARmax和最大体积分数fVRmax。此时的刺碰概率(PS)亦与实际最大刺碰概率(PSRmax)趋于同步,即

(11)

将等效直径de和颗粒最大投影面积的外接圆直径dmax代入式(10)和式(11),可计算得fAmax=0.785 4,fARmax=0.703 2。金刚石颗粒两种投影形状(A01和A02)的直径和刺碰概率PS的对比详见表1。本文选取由金刚石颗粒的最大投影面积作为其最为致密排列的理论填充面积(或体积)分数上限的等效直径de,进行后续计算、讨论与分析。此选择的优势在于:1)能够使无机颗粒在刀具作用下可能发生侧向挤压而产生的防刺阻力得以表征;2)可使无机颗粒的填充密度增大,尤其是在复合树脂片的表层,从而提高刺入力的横向传播速度,增大承力面积;3)因金刚石的受力变形几乎为零,则面积分数fAmax>π/4只能是颗粒直径不匀导致的。

表1 金刚石颗粒2种投影形状的直径(盒边长)和刺碰概率PS值

2.1.3 刺碰概率PS与体积分数fV和质量分数fm的关系式及结果对比

同理,在已知金刚石颗粒体积分数fV的情况下,假设复合树脂片中的金刚石颗粒为各向同性的均匀分布,则其截面积分数fA等于体积分数fV,复合树脂片的刺碰概率PS为

(12)

式中:Ares、AP总、A总分别为树脂、金刚石颗粒和复合树脂片的总面积。

若已知质量分数fm,可根据式(13)将fm转化为fV:

(13)

式中:mP总、mres、m总分别为金刚石颗粒、树脂和复合树脂片各自的总质量;ρP和ρR分别为金刚石颗粒和树脂的密度,ρP=3.5 g/cm3,ρR=1.4 g/cm3。

由式(13)可转化得到体积分数fV的通式和具体式,即

(14)

根据金刚石颗粒均布的假设,得fA=fV,结合式(12)可得刺碰概率PS,由此可计算得到不同金刚石颗粒体积分数与刀具刺碰概率及其差异倍数的关系,结果见表2。

表2 不同金刚石颗粒体积分数与刀具刺碰概率及其差异倍数的关系

由表2数据可知,复合树脂片厚度一定时,金刚石颗粒与刀具的刺碰概率随着金刚石颗粒体积分数的增大逐渐增大,且金刚石颗粒体积分数为14.63%和24.66%的树脂片与金刚石颗粒体积分数为6.59%的树脂片的刺碰概率差异倍数较大。此外,金刚石颗粒体积分数为24.66%的树脂片相对体积分数为14.63%的树脂片,刺碰概率提高了68.57%。

2.2 金刚石颗粒体积分数对复合树脂片防刺性能的影响

2.2.1 不同金刚石颗粒体积分数复合树脂片的防刺强力对比

为验证前文理论推导的正确性,制备了填充金刚石颗粒体积分数分别为6.59%、14.63%和24.66%的金刚石/PI复合树脂片及纯树脂片。对复合树脂片试样进行防刺性能测试,结果如图3所示。由图3可以看出,随着金刚石颗粒体积分数的增大,刺入复合树脂片的刀具载荷峰值即防刺强力F增大。除金刚石颗粒体积分数为24.66%时获得的曲线为单峰,其他试样在下降段均出现有刀具形态所致的肩胛峰。

图3 不同体积分数复合树脂片的刀头载荷(防刺强力)F与冲击刺入时间t的关系曲线

复合树脂片实测厚度、金刚石颗粒实测体积分数,以及由图3得到的复合树脂片防刺强力如表3所示。由表3可以看出,纯树脂片(金刚石颗粒体积分数为0%)的防刺强力为1 404 N,明显高于金刚石颗粒体积分数分别为6.59%和14.63%的2种复合树脂片的防刺强力。此不升反降的反常现象,为理论上的不可发生事件。根据对复合树脂片的观察结果可以发现,金刚石颗粒分布不均匀,厚度也不均匀,刀口附近及内壁上存在孔洞,并且金刚石颗粒与PI树脂间存在间隙及金刚石颗粒脱落产生的孔洞。因此可以认为,导致含金刚石颗粒复合树脂片强度低于纯树脂片的主要原因在于:1)金刚石颗粒分布不匀,这影响刀具与金刚石颗粒的刺碰概率,进而影响防刺性能;2)复合树脂片中存在气泡孔洞,以及颗粒与树脂间的间隙,这影响复合树脂片的强韧性;3)复合树脂片存在明显的厚度不匀,由试验测得的不匀值达15%。加之试验中同一块试样仅刺3次,其防刺强力的极差最高达568 N,而每片的平均差亦达20%。

表3 不同金刚石颗粒体积分数复合树脂片的防刺性能测试结果

图4 复合树脂片防刺强力与金刚石颗粒体积分数的关系曲线

2.2.2 复合树脂片刺扎后的刀口洞形貌对比

除了刀具载荷,还可通过刀具楔入不同体积分数复合树脂片的刀口洞面积和体积来表征复合树脂片的防刺效果。本文采用GA 68—2019《警用防刺服标准》中的A类刀具(双面刃)进行防刺试验。随着刀具刺入深度的增加,刺入刀口洞的形状也会发生变化(表4),故其亦可作为复合树脂片防刺功效的对比验证。

表4 刀具楔入不同金刚石颗粒体积分数复合树脂片的刀口形态参数

由表4数据可得刀具刺入体积(VS)与刀口洞面积(AS)随金刚石颗粒体积分数(fV)变化的关系曲线及回归方程,并对2条关系曲线进行对比,见图5。由图5可以看出,AS与fV为线性关系,而VS与fV则为非线性关系。2个曲线方程的形式基本一致,仅c值上相差0.3,其原因为前述3种作用(碰撞阻挡、反向切割和颗粒下移摩擦阻尼作用)机制所致[13]78;而且VS与fV关系曲线的c=3/2,正好符合体积与面积幂次方比值关系。因此,防刺强力(F)与金刚石颗粒体积分数(fV)的非线性关系再次得以证明,同时,对比VS和fV的关系曲线(图5)与复合树脂片防刺强力和金刚石颗粒体积分数的关系曲线(图4)可知,两者为互补关系。VS和fV的关系曲线既能提供刀具表面挤压摩擦的阻尼能耗,又能表达刀具头端截面积扩张的阻尼能耗,由此,两者呈非线性关系。

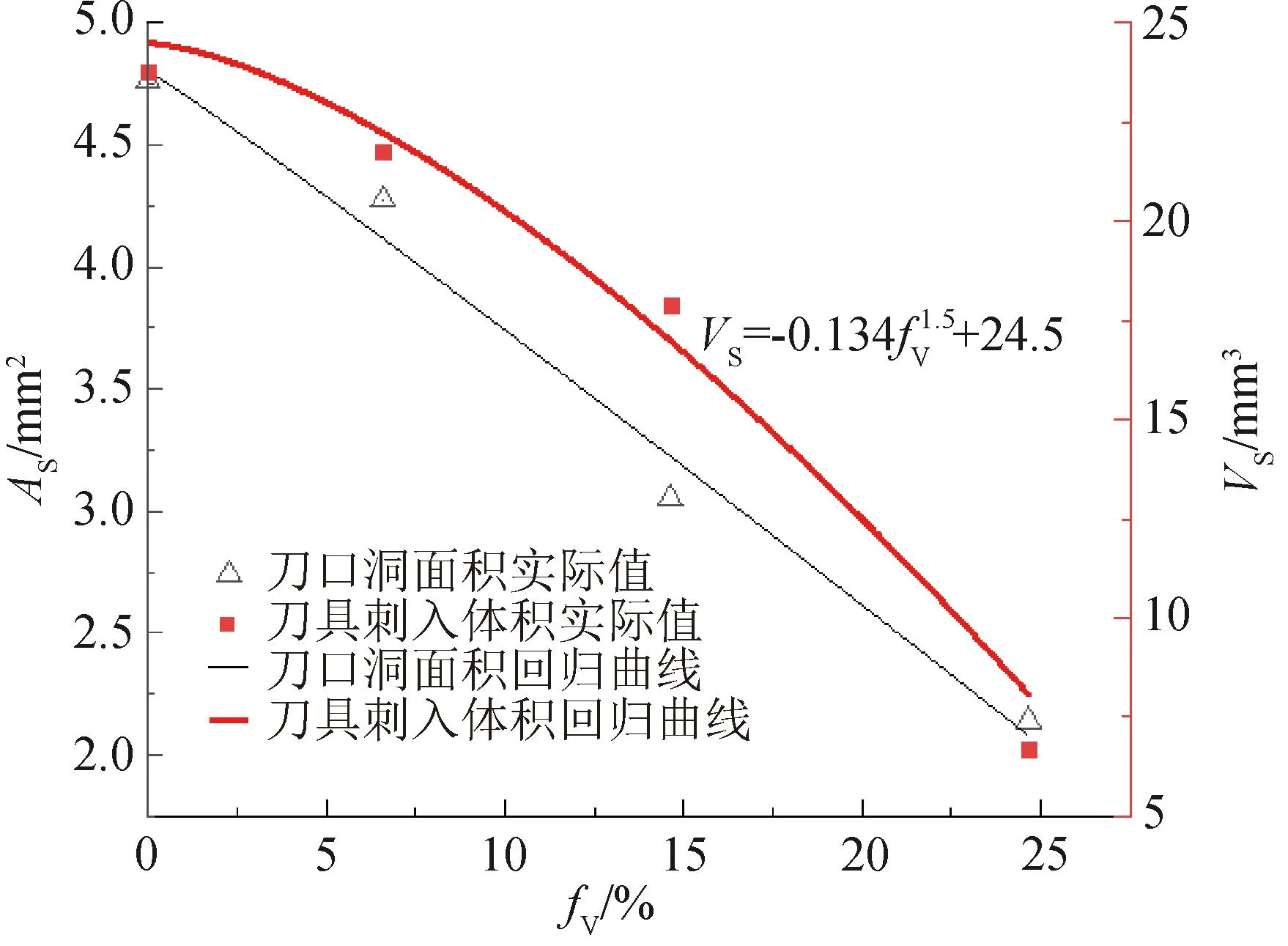
图5 刀具刺入体积与刀口洞面积随金刚石颗粒体积分数的变化关系曲线

不同金刚石颗粒体积分数复合树脂片受刀具刺扎后的刀口洞形貌如图6所示。结合表4和图6可知,随着金刚石颗粒体积分数的增大,复合树脂片的刀具刺入体积和刀口洞面积逐渐减小,形态也有所变化,这直观反映了复合树脂片的防刺性能随金刚石颗粒体积分数的增大而增加。同时由图6还可看到复合树脂片表层的颗粒分布不匀,并且刀头附近存在孔洞的现象。图6d)中,刀具刺入区域的金刚石颗粒密度高,而图6b)和图6c)中,刀具刺入区域的颗粒密度较低,且分布不匀。

图6 不同金刚石颗粒体积分数复合树脂片受刀具刺扎后的刀口洞形貌

3 结论

(1)金刚石颗粒在复合树脂片中均匀分布与否对其防刺性能的影响显著。金刚石颗粒分布不匀将直接导致刺碰概率的振荡和下降;颗粒分布均匀时,刀具和金刚石颗粒的刺碰概率与金刚石颗粒的体积分数呈正相关。此外,采用体积分数比采用质量分数能够更准确地表达防刺功效,更能反映金刚石颗粒与刀具碰撞的体积效应。

(2)复合树脂片的防刺强力与金刚石颗粒的体积分数呈非线性正相关,且有0.8个幂次方的增加;刀具刺入体积VS和fV的关系曲线与防刺强力F和fV的关系曲线基本一致且为互补函数,这不仅验证了防刺强力与金刚石颗粒体积分数的非线性正相关关系成立,而且证实了防刺强力的变化与刺碰概率的理论推导式及其幂次方数相吻合,这为高效防刺复合树脂片的制备提供了定量化的依据。