基于核系数样本选择算法的光谱模型更新

贺忠海，曹功伟，贾 琼，张晓芳

（1.东北大学秦皇岛分校 控制工程学院，河北 秦皇岛 066004；2.河北省微纳传感重点实验室，河北 秦皇岛 066004；3.北京理工大学 光电学院，北京 100081）

红外光谱测量数据必须与多元回归模型结合才能得到被测物浓度，在建立模型过程中需要采集一定数量的样本才能进行，从而提出了模型应用域（Application domain）［1］的概念，即用于预测的新样本必须位于建模过程中所用的标定旧样本的区间内才能得到正确的预测结果［2］。如果新样本超出应用域，需对模型进行更新才能适用于新样本［3］。此时，旧样本中虽有部分信息发生改变，但仍有很多信息具有利用价值，因而建立包含新的化学或仪器变化的额外标定样本的新模型即可适用于新环境，无需丢弃所有旧样本重新建模［4］。

当检测到新颖样本，通常希望尽快更新模型以使模型能适应新变化，但此时新样本的量通常占比较少，其新特性无法很快体现在模型中。为解决此问题，Stork 和Kowalski［5］提出了一种基于杠杆值的准则为新样本赋予合适的权重，以改善新旧样本间的不平衡。Capron和Walczak［6］发现选择有代表性的新样本有利于模型更新。由于模型更新的加权方法等同于对样本进行多次重复采样，导致样本中包含的噪声也被重复和放大，从而导致样本集中的噪声分布不再符合正态分布，影响建模效果。随着正则化技术的广泛应用，出现了把新样本预测误差作为正则化项进行优化的模型更新方法［7-8］，其本质等同于新样本加权。

为进一步加快模型对新环境的适应，需对旧样本进行选择以减少旧样本的数量。如无监督方法KS方法［9］、有监督选择方法SPXY［10］、基于基准值选择（YR）［11］，以及基于主动学习的样本选择方法［12］。但这种距离最大化的选择方法并不能保证所选择的样本有最大的模型贡献度。现有的对设计矩阵（自变量矩阵X）进行选择的工作通常以波长作为自变量，也诞生了很多依据自变量系数进行变量选择的方法［13］，但此类方法无法判断每个样本对建模的贡献。要判断各样本对建模的贡献度，仍 需寻找按样本分配回归权重的方法。

本文基于核函数系数，其中样本对应核函数系数的绝对值越大则样本越重要。通过在全部旧样本中选择部分系数绝对值大的样本，在选择部分旧样本基础上加入新样本。这种样本选择方法既考虑了特定分析物，又充分提取了旧样本包含的有用信息。通过将新旧样本组成混合的训练集，重新建立更新后的模型，从而快速获得所需实验结果。

1 建模方法的理论基础

现有的建模方法可以分为两大类，基于非相似性的建模（例如多元线性回归（MLR）、PLS 等）和基于相似性的建模（例如k近邻、支持向量机（SVM））。在通常的应用中，两类模型有不同的计算方法。非相似性方法（以PLS 为代表）的目的是找到每个变量对应的回归系数，相似性方法（以SVM 为代表）的目的是找到每个支持向量（部分样本）的权重。两类方法分别对应于建立以变量为基的模型和以样本为基的模型，也就是分别对设计矩阵（自变量空间X）进行针对列的变换和针对行的变换。由于根本处理对象的不同（行或列），虽然二者具有相同的优化目标函数，但两种方法并无共用的案例。

1.1 PLS

PLS中x和y之间的关系是线性关系，目标函数可表示为［14］：

1.2 核模型

核模型是以训练样本为基，基于待测样本与训练样本相似性建立的回归模型。用n个样本构成的核模型如式（3）所示：

将训练样本xi代入式（3）可得其预测值，则n个样本的预测值ŷ=Kθ，式中K为将n个训练样本代入核函数求得的核矩阵：

核模型的θ值可通过最小化求得 ，即θ=K+y，式中K+为核矩阵的伪逆，通过奇异值分解（SVD）得到，y为n个训练样本的标定值。

1.3 核模型与PLS的对等关系

PLS与核模型是从不同角度建立的回归模型，在机器学习中任何统计模型均可表示如下［15］：

PLS 和核模型的建模方法等价。从而将基于非相似性的PLS 建模方法和基于相似性的核建模方法统一，用两种方法建立的拟合函数是同一个回归模型。基于这样的统一，即可利用标定样本前的系数θi确定每个样本的重要程度，从而克服PLS 无法对样本重要性进行判断的缺点，同时保留PLS 模型易计算的优点。因此，基于相似性建模的核模型系数选择的重要样本，同样也是基于非相似性建模的PLS模型的重要样本，利用核系数选择的重要旧样本可用于PLS模型的更新。

2 利用核系数选择部分旧样本更新PLS模型

选择部分旧样本用于模型更新的方法包括两个步骤：（1）所有旧样本建立一个高斯核模型，利用每个样本对应的核函数系数确定样本的重要程度和选择部分旧样本，这种样本选择方法称为核系数选择（Kernel Coefficient Selection，KCS）；（2）在选择的部分旧样本基础上加入新样本更新PLS 模型。模型更新方法的流程图如图1所示［16-18］。

3 实 验

为验证本文选择样本方法的有效性，分别设计在模拟数据集和真实数据集上进行样本选择后更新模型。常见的数据偏移类型有协变量偏移、条件偏移和先验偏移3种［19］。本实验采用模拟光谱验证条件偏移的情况，采用实际数据验证先验偏移的情况。

3.1 模拟数据

光谱的吸收峰用正态概率密度函数代表，不同位置处的峰代表不同的成分。通过对旧样本中添加新成分产生条件偏移性质的光谱。新旧样本的模拟光谱分别表示如下：

表1 新旧样本集的参数值Table 1 Parameter values of the old and new sample sets

共模拟了200个旧样本和150个新样本，不同类型的光谱如图2所示。从图2可看出旧样本与新样本光谱有明显差异，在加入新成分后新样本的光谱多了1个特征峰。

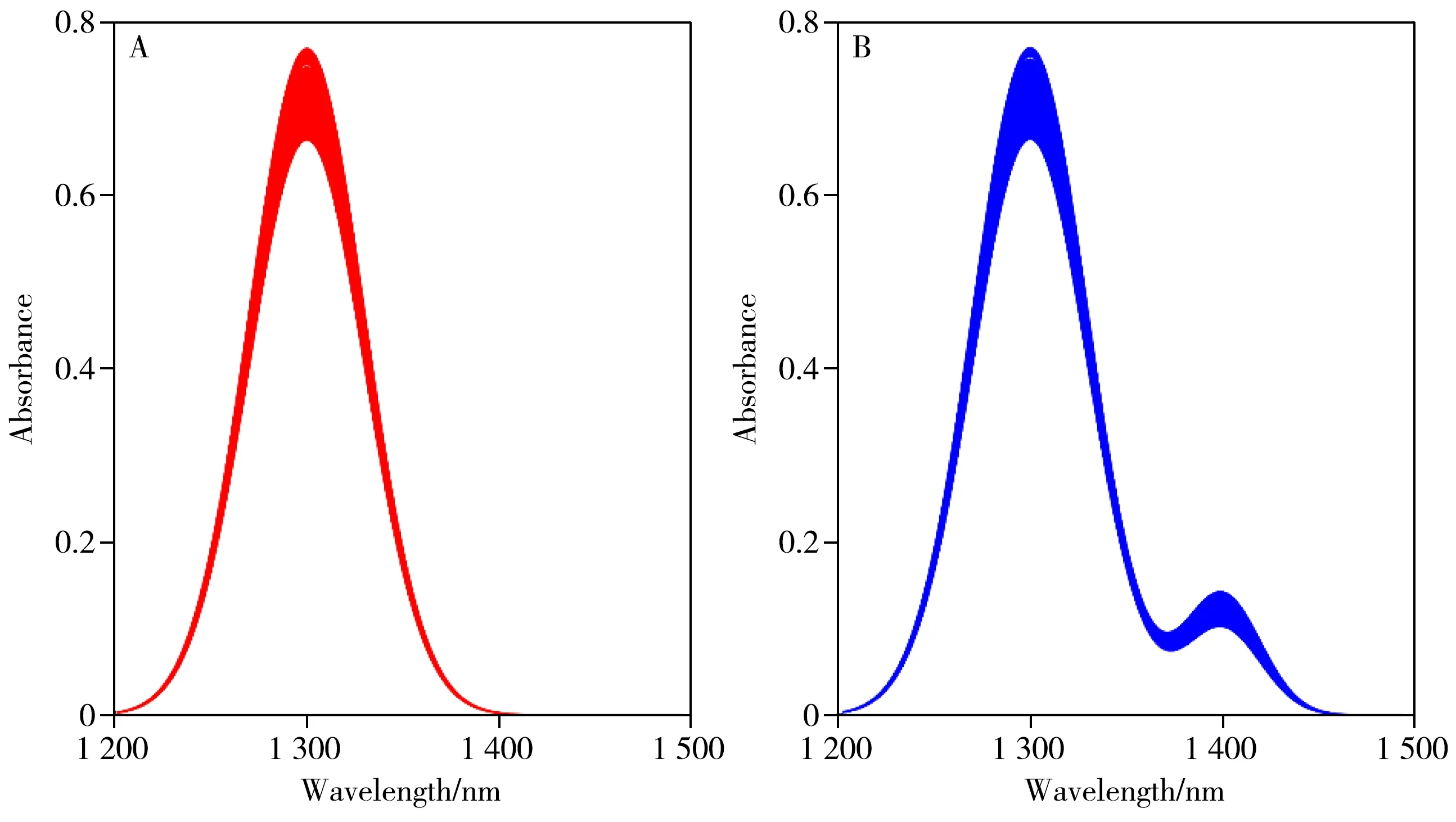
图2 不同样品数据集的光谱图Fig.2 Spectra of the simulated data with different samples

3.2 真实数据

为验证所提方法的性能，在豆粕数据集上进行实验研究。以2021年收集的200个样本作为旧样本，2 0 2 2年收集的1 5 0个样本作为新样本，总共收集了3 5 0个豆粕样本，使用二极管阵列分析仪在9 5 0 ～1 650 nm 的近红外区域以5 nm 的增量通过反射进行测量。采用蛋白质作为特定分析物建模，采用GB 5009.5-2010中规定的凯氏定氮法［20］对其含量测量，仪器为NYK6160分析仪（上海亿宏分析仪器有限公司）。豆粕数据集的可视化如图3 所示。从图3A 可以看出旧样本与新样本间的光谱差异较大，图3B 显示旧样本和新样本的蛋白质浓度（Y）分布不同。

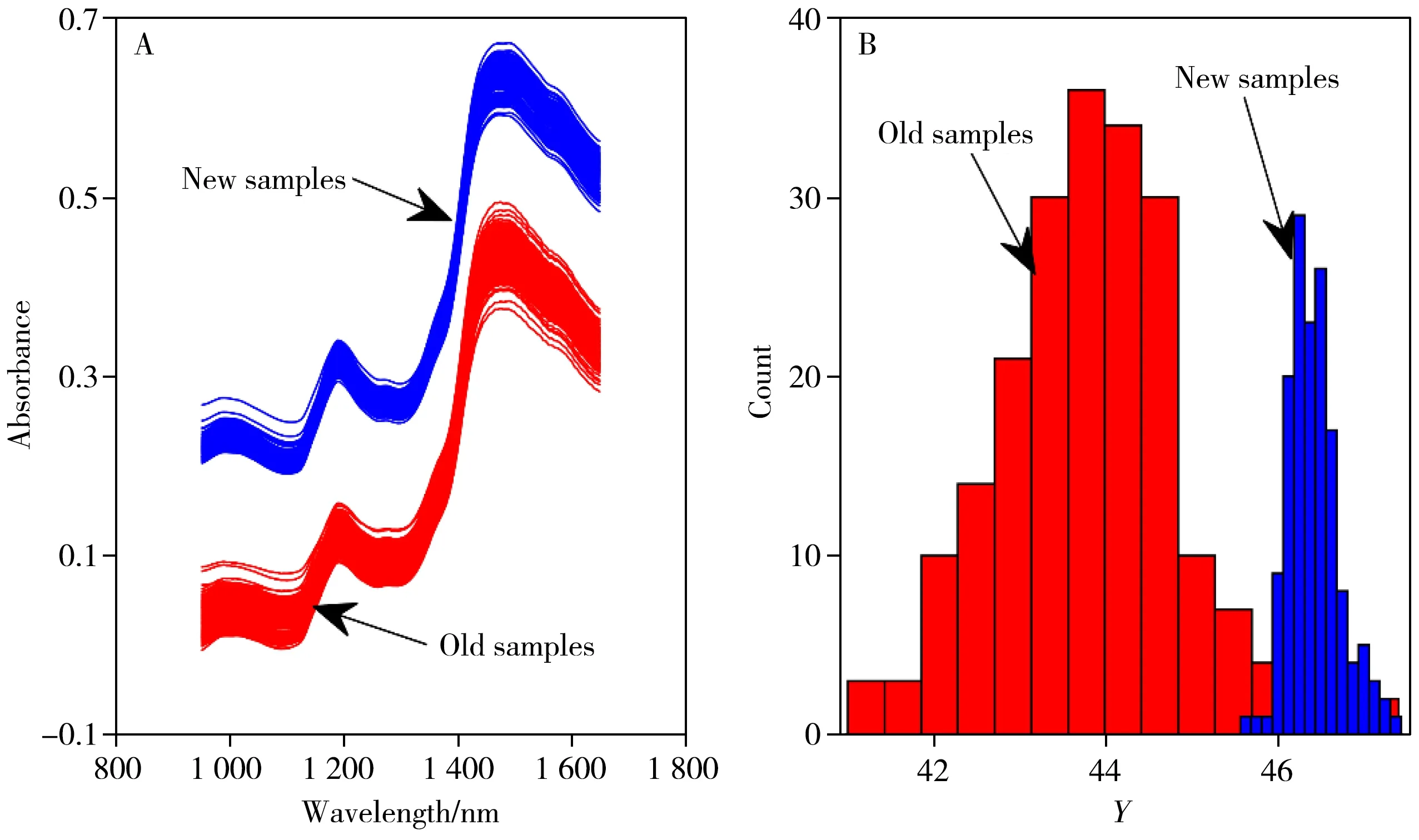
图3 真实数据集的光谱（A）和蛋白质浓度（B）分布Fig.3 Spectra（A） and protein concentration（B） distributions of the real data

3.3 评估策略

从200个旧样本中随机挑选60个样本作为旧样本的验证集，剩下140个样本作为校正集。从150个新样本中随机挑选45 个样本作为新样本的验证集，剩下105 个样本作为模型更新时新样本的候选集。分别用RS、KS、KCS在全部校正集里选出部分校正集建立模型并用全部校正集（TOTAL）建立模型，在旧样本的验证集上测试以评估RS、KS、KCS选择样本的性能。

用标准差（SD）反映不同样本集含信息量的多少，SD越大的样本集包含的信息越多。预测均方根误差（RMSEP）则作为模型的评价指标用于比较所建模型的预测效果，为进一步评价不同方法选择样本的建模效率，提出了预测均方根误差的相对偏差：

式中，I表示RS、KS、KCS样本选择方法，rI值越小表明该方法选用部分训练集建立的模型预测精度与全部训练集建立的模型预测精度越接近。

使用软件MATLAB R2018a在计算机上进行实验，实验所用的数据集和利用核系数选择部分旧样本的程序可在Github（https：//github.com/nandemihu/KCS.git）上获得。

4 结果与讨论

4.1 KCS方法选择部分旧样本的建模效果

表2列出了全部校正集和选择50个校正样本分别建立模型，用旧样本验证集进行测试的实验结果。可以看出全部校正集建立模型的预测均方根误差最小，这是由于全部校正集包含的有用信息最多。KCS 法选择部分校正集的SD 值接近全部校正集的SD 值，表明能够包含全部校正集里的大部分有用信息，KCS法选择部分校正集的RMSEP 与全部校正集的RMSEP 的相对偏差（rI)最小，表明模型的预测精度接近。因此采用KCS法选择部分校正集用于后续的模型更新。

表2 未加入新样本时部分校正集或全部校正集的建模预测结果Table 2 Modeling predictions for part or all of the correction set when no new samples are added

4.2 模型更新后对新样本的预测能力

图4 显示了KCS 选择部分校正集和全部校正集的基础上逐步添加新样本进行模型更新后，对新样本验证集的预测结果。结果显示，随着新样本的加入，新样本在校正集中的比例越来越大，RMSEP不断下降。其中TOTAL的RMSEP的下降速度慢于KCS，这是由于使用全部校正集用于模型更新可减弱新样本对模型的影响，而选择一部分校正集用于模型更新可使新样本占有更大的比重，有利于加快模型更新的速度。表3列出了模型更新前和加入20个新样本更新后对新样本验证集的RMSEP，可看出模型更新后的预测精度大幅提高，且用KCS 选择部分校正集后加入新样本更新后，模型精度提高更加显著。

表3 模型更新前后对新样本验证集的预测结果Table 3 Prediction results of the new sample validation set before and after the model update

4.3 模型更新后对旧样本的预测能力

图5 显示了在KCS 选择部分校正集和全部校正集的基础上逐步添加新样本进行模型更新后，对旧样本验证集的预测结果，可以看出随着新样本的加入，RMSEP 上升的比较平缓。表4 列出了模型更新前和加入20个新样本更新后对旧样本验证集的RMSEP，可看出模型更新后对旧样本验证集的预测精度有所下降，但仍有较强的预测能力，说明模型更新后对旧样本的预测能力影响较小。

表4 模型更新前后对旧样本验证集的预测结果Table 4 Prediction results of the old sample validation set before and after the model update

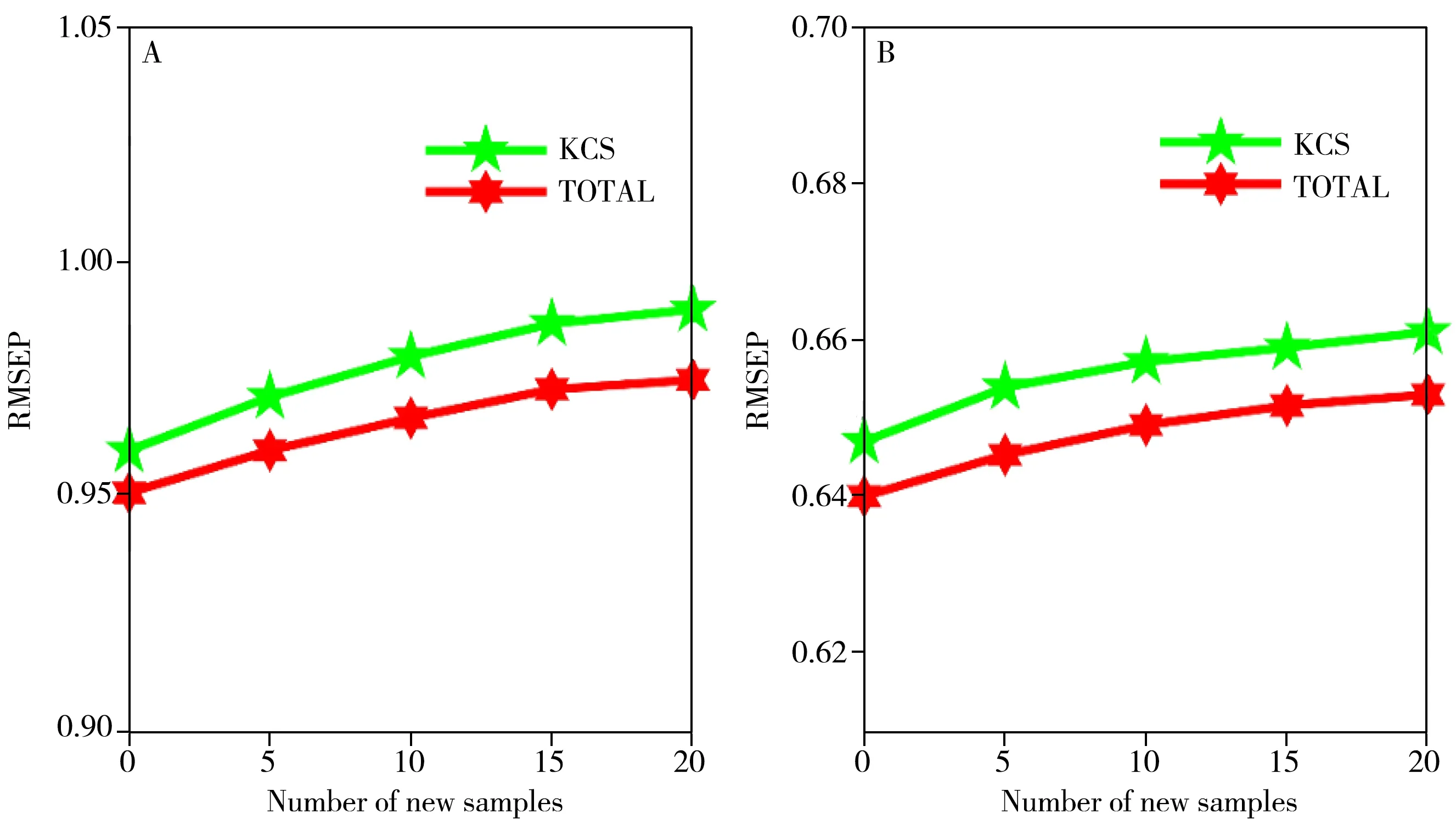
图5 逐步更新模型后对旧样本验证集的结果Fig.5 The results of the validation set on a old samples after the model is gradually updated

5 结 论

为解决模型更新中大量旧样本和少量新样本不能快速更新PLS 模型的问题，本文提出了一种基于高斯核系数的样本选择方法，用旧的校正集建立高斯核模型，再将每个样本所对应的高斯函数系数的绝对值从大到小排序，将排序靠前的部分校正集用于后续的模型更新。在部分校正集的基础上加入新样本重新训练模型，采用模拟数据集和真实数据集进行实验。用 KCS 选择部分校正集建立模型与RS、KS、TOTAL 进行对比实验，验证了KCS 选择的部分校正集的建模效果好、样本选择代表性强。再将KCS选择的部分校正集用于模型更新，结果显示，RMSEP 下降快，预测精度高。用更新后的模型预测旧样本的验证集仍可保持较好的预测精度。因此，这种基于高斯核系数的样本选择算法可用于大量的旧样本里选择部分旧样本更新，使模型快速地适应新环境。