大跨径斜拉桥索塔钢锚梁及牛腿板件受力分析
2024-01-02郑力之贺耀北
郑力之, 贺耀北, 李 瑜
(1.湖南省中南建设集团有限公司,湖南 长沙 410000; 2.湖南省交通规划勘察设计院有限公司,湖南 长沙 410200)
0 引言
斜拉桥是由承压的塔、受拉的索和承弯的梁体组合起来的一种结构体系[1-2],桥梁主梁上的荷载,通过斜拉索传导至索塔[3]。索塔锚固结构有很多种形式,对于钢索塔,常用的锚固形式有鞍座支承型、铰接锚固型、锚固梁型、支承板型等。而对于混凝土索塔,多采用塔壁锚固、钢锚梁锚固、钢锚箱锚固等[4-5]。
钢锚箱构造复杂,造价相对较高;钢锚梁锚固形式则受力清晰、施工便捷[5-6]。其中,采用钢牛腿的钢锚梁锚固结构,是形式较为新颖的索-塔锚固构件,其作为斜拉桥关键节点位置的主要传力构件,对于桥梁结构的安全极为关键,但该位置构造和受力情况均较为复杂,需要进行详细的受力分析以保证桥梁安全[7-9]。
1 依托工程概况
G59呼北高速官新段马路口资水特大桥为主跨500 m双塔双索面半漂浮体系组合梁斜拉桥,桥跨布置为(60+160+500+160+60)m,主桥长940 m,是湖南省最大跨径组合梁斜拉桥、第二大跨径斜拉桥(见图1)。塔采用H型索塔,塔柱为矩形空心截面,共设下、上两道箱形截面横梁,斜拉索为扇形布置[11]。

图1 马路口特大桥立面布置及钢锚梁编号(单位:m)
斜拉索塔端采用钢锚梁的锚固方式,钢锚梁主要承受斜拉索的平衡水平力。每套钢锚梁锚固1对斜拉索。索塔共有钢锚梁40套,单个塔柱包含20套,自下而上编号为GML1~GML20,如图1(b)所示,塔端索距布置为(3.5+2×3+3×2.75+13×2.5)m。钢锚梁总高度随钢锚梁类型及斜拉索倾角变化而变化。钢锚梁为箱形结构,由箱型拉板(顶板、底板、腹板、腹板外侧加劲板)、锚垫板、锚下承压板、锚下支撑板、横隔板及加劲板组成。钢牛腿是钢锚梁的支撑结构,由上承板、托架板、塔壁预埋钢板(含剪力钉以及与其连接的刚性预埋板)组成。钢锚梁及钢牛腿结构如图2、图3所示。

图2 钢锚梁结构示意

图3 钢牛腿结构示意
拉索锚头锚固于锚垫板之上,将索力传导至钢锚梁,钢锚梁自身承受一对拉索的反向水平分力,同时通过栓钉连接,将拉索竖向分力向下传导至钢牛腿,从而传导至索塔,钢锚梁及牛腿与塔壁的位置如图4所示。

图4 钢锚梁及牛腿与塔壁的位置示意
2 分析模型建立
对拉索塔上锚固区受力复杂的局部区域进行空间有限元应力分析,揭示塔端锚固区的实际受力特性及其应力分布规律,为索塔钢锚梁及牛腿结构设计提供依据,以保证结构的安全性与耐久性,采用Ansys大型通用有限元软件建立索塔钢锚梁及牛腿空间有限元模型。
2.1 计算参数
钢锚梁、钢牛腿钢材采用Q355D低合金钢,其技术指标均应符合《低合金高强度结构钢》(GB/T 1591-2018)的相关要求。各构件钢板厚度详见相关构造图纸,材料弹性模量E=2.06×105MPa ,容重γ=78.5 kN/ m3,泊松比ν=0.3,其抗拉、抗压和抗弯设计强度如表1所示。

表1 钢锚梁及牛腿钢材抗拉、抗压和抗弯强度设计值厚度/mm≤1616~4040~6363~8080~100设计强度/MPa283276264253249
有限元模型荷载边界条件根据主桥整体空间静力分析确定,整体空间计算模型中荷载(作用)考虑结构自重、二期恒载、预应力、汽车荷载、风荷载、温度效应(结构整体升温及降温、斜拉索与主梁及索塔温差)、混凝土收缩徐变等。具体荷载(作用)取值按照主桥整体空间静力分析计算得出,典型索力荷载工况及拉索索力如表 2所示。荷载(作用)按照《公路桥涵设计通用规范》(JTG D60-2015)第4.1节规定进行组合。

表2 典型荷载工况及拉索索力钢锚梁编号对应拉索编号拉索索力/kN边跨侧中跨侧边跨侧中跨侧GML20SB20SZ209 302.99 613.4GML5SB5SZ55 242.55 288.3GML2SB2SZ24 382.54 425.4GML1SB1SB14 380.74 342.4
2.2 有限元模型
索塔钢锚梁与牛腿空间有限元分析计算模型利用Ansys有限元软件建立,构件均采用Solid185实体单元,钢锚梁与牛腿几何模型及有限元模型分别如图5、图6所示。

图5 钢锚梁有限元模型
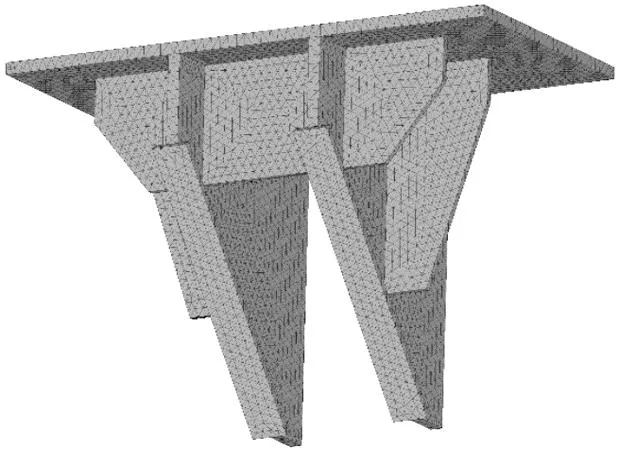
图6 钢牛腿有限元模型
2.3 边界条件模拟
位移边界条件为:①钢锚梁:对边跨侧钢锚梁底面与牛腿顶面共节点耦合;中跨侧钢锚梁底面与牛腿顶面施加不分离型面-面接触约束,允许滑移,不允许分离和穿透;②牛腿:对牛腿与塔壁交接面施加固结约束。
荷载边界条件为:①钢锚梁:将全桥整体静力分析所得拉索索力转化为分布面力施加于钢锚梁锚垫板上;②牛腿:钢锚梁响应及变形将通过公共节点以及面-面接触方程传递至牛腿。
3 计算结果与分析
3.1 钢锚梁计算结果
3.1.1GML20钢锚梁
GML20钢锚梁处于最长索位置,其倾角最小。各构件Von Mises应力计算云图如图7所示。

图7 GML20应力云图(单位:MPa)
计算分析表明,钢锚梁最大应力出现在顶板与腹板的焊接尖端,Von Mises应力峰值298.9 MPa,高于设计容许值,但该角点位置为应力集中点(见图8),且顶板绝大部分位置的应力值均远低于设计容许值,可认为顶板强度满足设计要求;腹板与底板的焊接尖端Von Mises应力峰值282.9 MPa,高于设计容许值,但该角点位置亦为应力集中点,且腹板绝大部分位置的应力值均远低于设计容许值,可认为腹板强度满足设计要求;其余钢锚梁构件应力较容许值均有一定富余,强度均满足设计要求。钢锚梁构件应力如表3中所示。

图8 GML20顶板应力分布(单位:MPa)

表3 GML20各构件应力计算结果MPa构件底板顶板腹板锚垫板锚下支承板其余构件强度设计值276276264264264276应力峰值233.4298.9282.9149.4181.7214.7
3.1.2GML5钢锚梁
GML5钢锚梁各构件Von Mises应力计算结果如表4所示,计算分析表明钢锚梁最大应力出现在锚下支撑板与腹板的焊接尖端,Von Mises应力峰值134.6 MPa,远低于设计容许值;其余钢锚梁构件应力较容许值均有一定富余,强度均满足设计要求。

表4 GML5各构件应力计算结果MPa构件底板顶板腹板锚垫板锚下支承板其余构件强度设计值276276264264264276应力峰值114.132.78129.6790.14134.689.9
3.1.3GML2钢锚梁
GML2钢锚梁各构件Von Mises应力计算结果如表5所示,计算分析表明钢锚梁最大应力出现在锚下支撑板与腹板的焊接尖端,Von Mises应力峰值214.1 MPa,远低于设计容许值;其余钢锚梁构件应力较容许值均有一定富余,强度均满足设计要求。
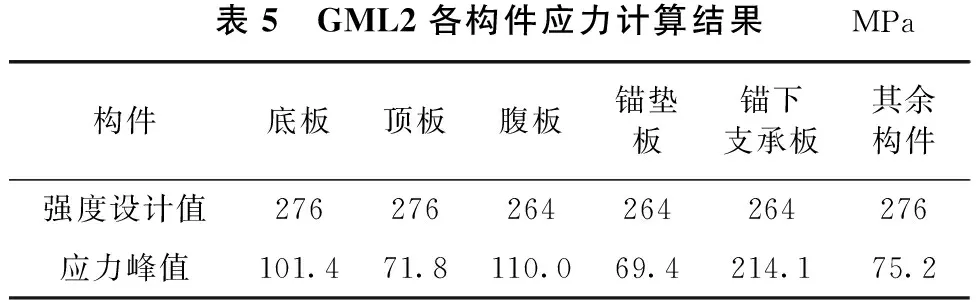
表5 GML2各构件应力计算结果 MPa构件底板顶板腹板锚垫板锚下支承板其余构件强度设计值276276264264264276应力峰值101.471.8110.069.4214.175.2
3.1.4GML1钢锚梁
GML1钢锚梁所在位置斜拉索倾角最大(见图9),其各构件Von Mises应力计算结果如表6所示,计算分析表明钢锚梁最大应力出现在锚下支撑板与腹板的焊接尖端,Von Mises应力峰值213.7 MPa,低于设计容许值;其余钢锚梁构件应力较容许值均有一定富余,强度均满足设计要求。

图9 GML1应力云图(单位:MPa)

表6 GML1各构件应力计算结果MPa构 件底板顶板腹板锚垫板锚下支承板其余构件强度设计值276276264264264276应力峰值85.852.7138.988.1213.773.8
3.1.5钢锚梁计算分析
由实体有限元模型计算结果可知,在典型索力荷载工况下,仅有部分局部位置存在应力集中现象,绝大部分钢锚梁各板件Von Mises应力小于强度设计值,满足要求。
图10为各型钢锚板件峰值应力变化,从应力响应规律可以看出,整体上,板件应力随着索力降低而降低;值得注意的是,GML20峰值应力出现在顶板角点,GML5~GML1峰值应力均出现在锚下支承板。分析可知,拉索倾角小的位置(以GML20所在位置为代表),索力大,水平拉力也大,钢锚梁主要受力为平衡一对拉索的水平拉力,因此应力峰值出现在顶板的弧形开口角点上,符合受力和构造;拉索倾角大的位置(以GML1所在位置为代表),水平拉力小,钢锚梁主要受力为承担拉索传递的主梁竖向重力,受力方向明确,受力主要为向下的压力,因此应力峰值出现在锚下支承板,符合受力和构造。

图10 各型钢锚梁板件峰值应力变化
3.2 钢牛腿计算结果
3.2.1GML20钢牛腿
GML20钢牛腿处于最长索位置,其倾角最小。其各构件Von Mises应力计算云图如图11所示。

图11 GML20钢牛腿应力云图(单位:MPa)
计算分析表明,GML20钢牛腿最大应力出现在上承板、托架板、索塔壁板,三板交界角点位置,Von Mises应力峰值181.2 MPa,低于设计容许值,且富余较大;其余牛腿构件应力均小于该应力峰值,强度满足设计要求。钢牛腿构件应力如表7中所示。
3.2.2GML5钢牛腿
GML5钢牛腿各构件Von Mises应力计算结果如表8所示,计算分析表明牛腿最大应力出现在竖向加劲板与托架板连接下端部,其Von Mises应力峰值199.7 MPa,低于设计容许值;其余牛腿构件应力均小于该应力峰值,强度满足设计要求。
3.2.3GML2钢牛腿
GML2钢锚梁下牛腿各构件Von Mises应力计算结果如表9所示,计算分析表明牛腿最大应力出现在竖向托架板与加劲板连接下端部,Von Mises应力峰值219.1 MPa ,设计容许值;其余牛腿构件应力均小于该应力峰值,强度满足设计要求。

表9 GML2各构件应力计算结果MPa构 件上承板托架板加劲板翼托架缘板强度设计值276276276276应力峰值150.7197.4219.1101.1
3.2.4GML1钢牛腿
GML1钢牛腿各构件Von Mises应力分布云图如图12所示,应力计算结果见表10。计算分析表明牛腿最大应力出现在托架加劲板与上承板连接的端部,Von Mises应力峰值210.5 MPa,托架板强度满足设计要求;竖向加劲板与托架板连接的端部,Von Mises应力峰值224.8 MPa,加劲板强度满足设计要求;其余牛腿构件应力均小于该应力峰值,强度满足设计要求。

图12 GML1钢牛腿应力分布(单位:MPa)

表10 GML1各构件应力计算结果 MPa构件上承板托架板加劲板翼托架缘板强度设计值276276276276应力峰值162.5210.5224.887.5
3.2.5钢牛腿计算分析
由实体有限元模型计算结果可知,在典型索力荷载工况下,钢牛腿各板件Von Mises应力小于强度设计值,满足要求。
各型钢牛腿板件峰值应力变化如图13所示,从应力响应规律可以看出,随着拉索倾角增大,钢牛腿的板件应力整体承增大趋势。在拉索倾角较小的位置(GML20为代表),峰值应力出现在上承板角点位置;而随着拉索倾角增大,托架板、加劲板的受力明显增加,以GML1为代表位置处拉索倾角最大,受力接近于竖向,荷载主要转为托架板及托架加劲板承受。

图13 各型钢牛腿板件峰值应力变化
值得注意的是,上承板在GML5~GML1几个位置,也有些许应力上升,分析可能原因,是由于拉索位置板件开孔,导致板件面积减小,几何角点增加的缘故。
4 结论
本文以G59呼北高速官新段马路口资水特大桥斜拉索塔端锚固系统为研究对象,探究钢锚箱及钢牛腿的受力状态与响应规律,得到如下结论:
1)从各型钢锚梁板件峰值应力响应规律可以看出,整体上,板件应力随着索力降低而降低;拉索倾角小的位置,索力大,水平拉力也大,应力峰值出现在顶板的弧形开口角点上,因此长索区对应的钢锚梁在设计上应重点考虑该区域;拉索倾角大的位置,水平拉力小,钢锚梁主要受力为承担拉索传递的主梁竖向重力,受力方向明确,应力峰值出现在锚下支承板,因此短索区对应的钢锚梁在设计上应重点考虑该区域。
2)从各型钢牛腿板件峰值应力响应规律可以看出,随着拉索倾角增大,钢牛腿的板件应力整体承增大趋势。在拉索倾角较小的位置,峰值应力出现在上承板角点位置;随着拉索倾角增大,托架板、加劲板的受力明显增加,荷载主要转为托架板及托架加劲板承受,在设计中应针对性考虑。且短索区应进一步考虑拉索位置板件开孔对板件安全性的影响。
3)计算分析表明,各个荷载工况下,各板件的应力峰值均出现在板件相交或构件角点位置,表现出明显应力集中情况,而在设计和实际情况中,焊缝也基本布置在这些区域,结构脆弱位置出现应力集中将带来安全隐患,因此钢锚梁及牛腿制作过程中,应采取圆弧倒角等有效措施,消除焊接残余应力,增加结构安全性。
4)根据分析结论,对重点构件的重点位置进行针对性施工监控,能更高效地保证施工质量,更合理地进行资源配置。
5)由实体有限元模型计算结果可知,在典型索力荷载工况下,钢锚梁仅有部分局部位置存在应力集中现象,但钢锚梁各板件Von Mises应力小于强度设计值,满足规范要求;钢牛腿各板件Von Mises应力小于强度设计值,满足要求。但由各板件应力计算结果可知,各板件应力冗余不同,在运营管养中亦应相应制订具有侧重点的管养策略。
