小区域气象要素不同方法插值的性能分析

张颖超,行鸿彦,李浩琪,吴叶丽

(1.南京信息工程大学江苏省气象灾害预报预警与评估协同创新中心,南京 210044;2.南京信息工程大学江苏省气象探测与信息处理重点实验室,南京 210044)

0 引言

在区域农业、环境、生态、GIS等研究领域,气温、相对湿度等的空间化是重要参考因素,并被引入模型研究。这就要求实测台站提供准确的监测结果,便于相关技术人员开展相应的研究[1]。但是自动气象站的实测数据属于点数据量,仅能代表该测站附近局部地区的实际气象条件,而无法精确表达附近更大区域的实际天气状况[2-4]。为了将最精确的天气数值信息及时提供给需要的部门,以保障人们日常出行不受气象原因的限制,文章通过收集监测地区的气温、相对湿度等气象要素数据,对数值进行可视化处理,使气象要素信息的展示更直观。

空间内插法可以将小区域的气象要素分布显示出来,分为确定性和地统计2种插值算法[5]。确定性插值利用对象的空间相似性,或以平滑度为基础,根据已知样本点创建表面;地统计插值不仅要考虑对象的空间相关性和依赖性,还要考虑对象的统计特性。离散显示是对某一时间点各个采集点气象要素进行数据采集并显示出来;连续显示是对同一时间点整个区域范围内的气象要素数据进行分析,将该区域的气象要素分布图显示出来。相比离散显示,连续显示有着更明显、更全面的优点,通过连续显示得到的气象要素分布图能够有效地观测当日的天气状况,大大减少了因天气原因导致的各种问题。

目前,有许多研究人员对某一区域的气象状况进行分析,如李金洁等[6]采用确定性插值方法中的IDW法与地统计插值中的OK法对西南地区的月均降雨量进行空间插值,并得出OK法的插值效果更好;周淑玲[7]对福州市城区空气中的PM10浓度进行分析,采用三种方法进行空间插值,得出OK法空间插值效果最理想;徐谢亲等[8]采用三种插值算法对江西省年平均气温进行空间插值,得到IDW法插值效果最好。不同插值方法受到不同因素的影响,得到的效果各不相同。

文章利用反距离加权内插法,以南京信息工程大学西苑老食堂及周边区域的气象观测要素为原始数据,对数据进行预处理,在ArcGIS软件平台上,通过改变幂指数的值,对气温、湿度、气压进行处理。在同一时间下,与普通克里金内插法进行比较,通过分析各气象要素的空间分布特征及对比交叉验证结果,比较两种方法的优劣,实现较高的准确性和清晰性。

1 空间插值方法

空间数据内插是指根据一组已知的离散数据或分区数据,按照某种数学关系推求出其他未知点或未知区域数据的数学过程[9]。因此,从离散显示需要采集的单个数据,到连续显示对采集数据进行可视化处理分析得到气象要素分布图这一过程,需要采用内插法。文章采用交叉验证法来验证反距离加权内插法和普通克里金内插法的优化效果,并评价两种方法的优劣[10-11]。

1.1 反距离加权内插法

反距离加权内插法(简称“IDW法”)是一种基于相近相似原理的内插算法,即距离越近,相似性越大。该算法以插值点与样本点之间的距离为权重进行加权平均,越靠近插值点的样本点权重越大,影响越小[12]。计算公式如式(1)所示:

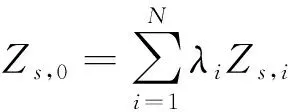
(1)

式中,Zs,0为s0处的预测值;Zs,i为si处的测量值;N为预测过程中所采用的预测点附近的采样点数目;λi为预测过程中已知样点的权重。λi的计算如式(2)所示:

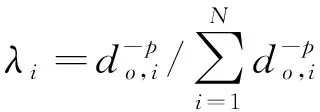
(2)

式中,do,i为预测点s0与各已知样点si之间的距离;p为幂指数。设定p指数可以对插值结果产生明显的作用,有研究发现,随着幂指数的增大,幂越高,插值结果变得更加光滑[13]。

1.2 普通克里金内插法

普通克里金内插法(简称“OK法”)是由克里金法演化而来的一种插值方法。若需对数据进行普通克里金插值,需要数据满足正态分布且应用极其广泛。基于区域化变量理论,半变异函数作为分析工具,研究具有随机性和结构性变量的空间分布具有一定的优越性。其本质是将半变异函数应用于未知样点的线性无偏优化估计。计算公式如式(3)所示:

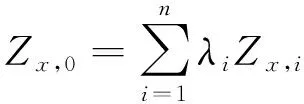
(3)

式中,Zx,0为x0处预测值;Zx,i为xi处测量值;λi为测量值对预测值的权重系数,为了使估计方差达到最小,可采用Chrikin方程组进行线性无偏估计。半变异函数γ(h)模型的选取是决定插值质量的关键因素,选取6种常用的半变异函数模型,对未知点进行预测。

1.3 检验标准

为了比较不同插值算法对插值效果的影响,可以通过交叉验证法检验。在进行插值法的对比时,必须考虑平均绝对误差(Ema)、相对误差(Emr)和均方根误差(Erms)。预测值的误差范围是通过平均绝对误差反映的,而相对误差体现了预测值的相对精确性,均方根误差反映了数据估值的敏感性和极值,分别如式(4)～(6)所示[14-15]:

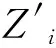
2 数据来源与预处理

此次监测范围为南京信息工程大学西苑老食堂以及文苑1栋、2栋区域。该区域位于学校的西北角,是食堂与宿舍的所在地,在学生吃饭与上课时间,人流较为密集,对该区域进行气象要素数据分析能够为学生以及其他人员的出行提供参考。除此之外,为了提高空间插值准确率,需要在插值分析前对采集点数据进行偏度和峰度分析。

2.1 数据来源

在监测区域内的不同位置安装5个气象要素采集系统,对该区域某日10:00—19:00时段的气温、湿度、气压数据进行采集,小区域范围如图1所示。5个采样点的分布较为均匀,能够预测该区域的3种气象要素数据。

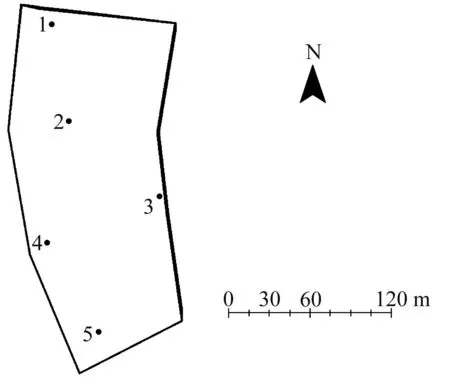
1—食堂靠北的马路;2—食堂靠南的马路;3—文苑1栋与2栋的东侧;4—文苑1栋与2栋的西侧;5—文苑1栋靠南的马路。图1 测量区域采集点分布

2.2 数据预处理

利用SPSS计算13:30采集点数据的偏度和峰度的Z评分(Z-score),描述统计如表1所示。在α=0.05的检验水平下,检验偏度Z-score和峰度Z-score是否满足假设条件所限制的变量范围(Z-score在-1.96～1.96),若都满足,则可认为服从正态分布,若有一个不满足,则认为不服从正态分布。

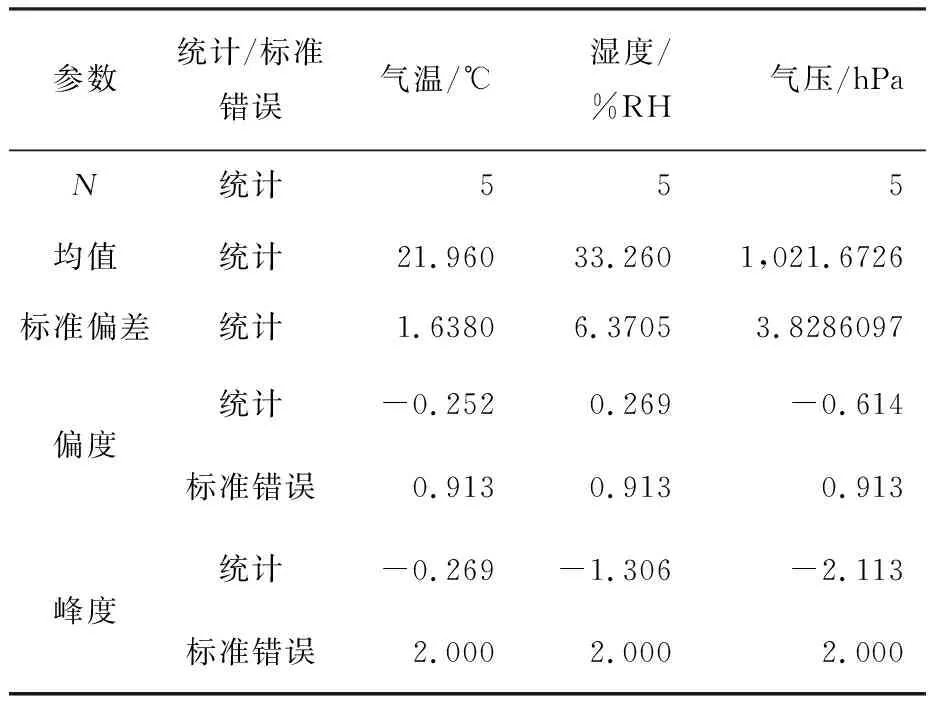
表1 偏度、峰度描述统计

偏度Z-score为偏度统计与偏度标准错误的比值,峰度Z-score为峰度统计与峰度标准错误的比值。由表1计算得出:气温、湿度、气压的偏度Z-score和峰度Z-score的值满足条件,因此气温、湿度、气压均服从正态分布,故后续在进行普通克里金插值时无需进行数据变换。

3 对小区域气象要素插值的性能分析

3.1 内插法的模型及参数优化分析

对IDW法的幂指数进行优化,对OK法的半变异函数模型进行选择后,可以得到最优参数与模型。需要借助ArcGIS软件平台,分析交叉验证结果。将采集点数据导入ArcGIS中,并转换为shapeflie数据,然后根据相关提示操作,完成相应的模型与参数优化。

3.1.1 IDW法的幂指数优化

为了得到较高的插值精度,需要选取合适的幂指数,此次采取的幂指数数值为p=1,2,3,4,5。幂指数优化结果如表2所示:1)当幂指数p=2时,气温的Ema和Emr最小;幂指数p=5时,气温的Erms最小。2)当幂指数p=4时,湿度的Ema和Emr最小;当幂指数p=5时,湿度的Erms最小。3)当幂指数p=2时,气压的Ema,Emr,Erms最小。因此,气压和气温均选取幂指数为2进行分析,湿度选择幂指数为4进行分析。

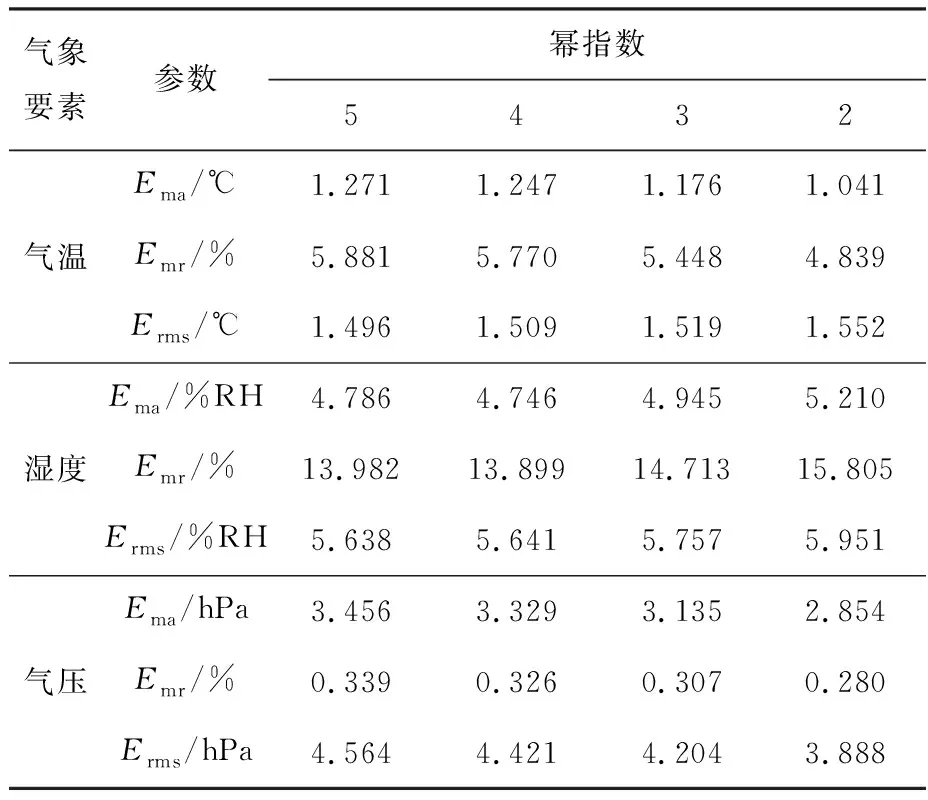
表2 IDW法幂指数优化

3.1.2 OK法的半变异函数模型选择

采用三角函数、球面模型等6种常用的半变异函数模型,完成OK法的最优模型选择。优化结果如表3所示:1)半变异函数为五球体模型时,气温的Ema,Emr,Erms的值最小;2)半变异函数为五球体模型时,湿度的Ema和Erms值为最小;3)半变异函数模型为球面函数模型时,气压的Ema,Emr的值最小,而在四球体模型下,气压的Erms值最小。因此,气温、湿度将使用五球体模型作为OK法插值分析的半变异函数模型,气压将使用球面函数模型作为OK法插值分析的半变异函数模型。

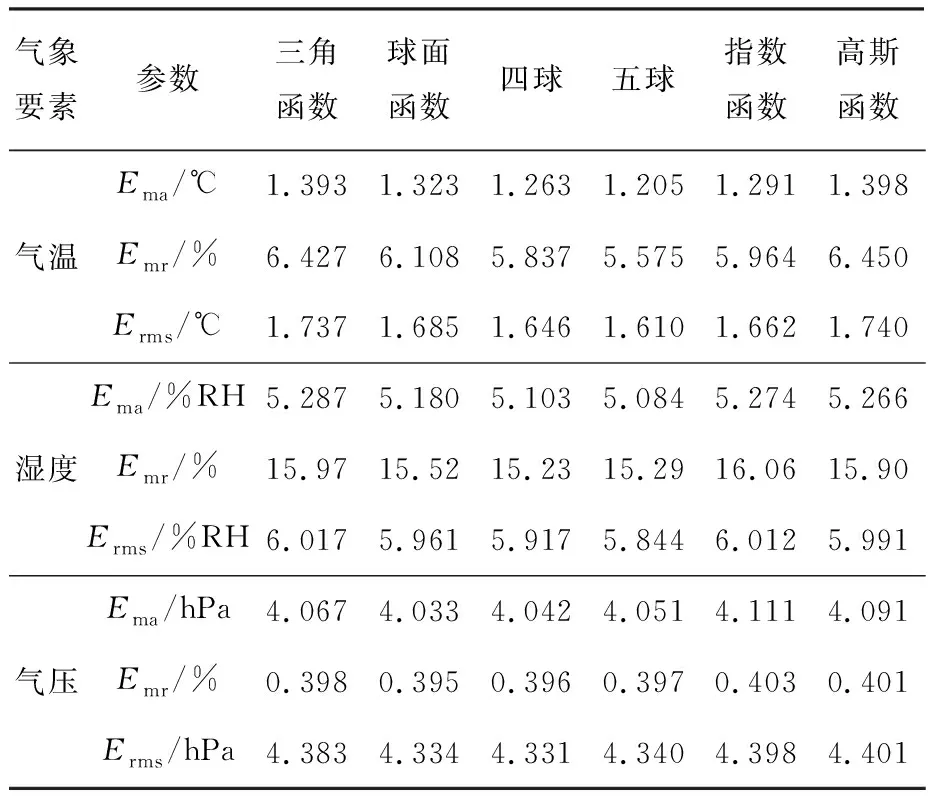
表3 OK法模型优化

3.2 空间分布特征分析与比较

根据模型选定和参数优化后的插值方法,对气温、湿度、气压进行空间分布特征分析并对交叉验证结果进行比较,得到最优插值方法[16]。

3.2.1 气温分布特征分析

气温整体的空间分布特点较为相近,只有部分空间上有差别。在测量区域内,北部温度略高,而南部温度略低,这是因为中午研究区域(老食堂)周围温度较高,小树林由于处在面向正南方的建筑物后,所以温度较低,其结果与实测点分布及实际观测结果相一致。从总体上看,OK法的结果比IDW法的结果平滑,但是OK法的预测值与实测值误差较大,如在采集点2采集到的气温数据为24 ℃,而使用OK法的预测范围在22.75～22.93 ℃,与实际不符。因此,IDW法更适用于该小区域的气温气象要素。

由表4可以看出,IDW法的Ema为1.041 ℃,Emr为4.839%,Erms为1.552 ℃;OK法的Ema为1.205 ℃,Emr为5.575%,Erms为1.610 ℃。比较2种方法的Ema,Emr和Erms,显示出相同趋势,即OK法>IDW法,因此,IDW法对该区域的气温的插值效果更好。这与气温空间分布特征分析的结果一致。

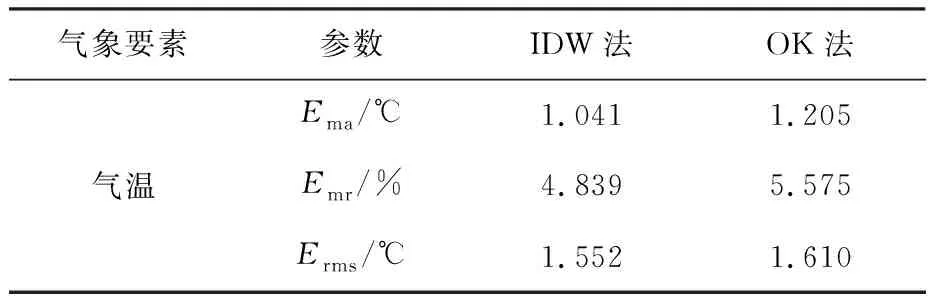
表4 气温的交叉验证结果

3.2.2 湿度分布特征分析

小区域的湿度与气温的空间分布特征总体上较为接近。在测量区域内,北部湿度略低,而南部湿度略高,这与温度分布的结果相关联[17]。经过比较可知,除了明显的采集点1与采集点3外,IDW法比OK法多1个位于采集点5的中心点,这与IDW法的原理有关,采集点离插值点越近则权重越大,影响越小。因此,对于小区域的气象状况分析,IDW法更适用于该区域的湿度气象要素。

由表5可以看出,IDW法的Ema为4.746%RH,Emr为13.899%,Erms为5.638%RH;OK法的Ema为5.084%RH,Emr为15.296%,Erms为5.844%RH。比较2种方法Ema,Emr和Erms,显示出相同趋势,即OK法>IDW法,因此,IDW法对该区域的湿度的插值效果更好。这与湿度空间分布特征分析的结果一致。

表5 湿度的交叉验证结果

3.2.3 气压分布特征分析

2种方法的气压分布有着较大区别,使用OK法得到的气压范围为1,020.33～1,022.56 hPa,但是5个采集点中无任何1个点的数据在此范围内,与实际不符。IDW法可以得到的中心点较多,并且能直观地看出5个采样点周围的预测结果,更能将小区域气压气象要素分布清晰、准确、有效地显示出来[18]。因此,IDW法更适用于该小区域的气压气象要素。

由表6可以看出,IDW法的Ema为2.854 hPa,Emr为0.28%,Erms为3.888 hPa;OK法的Ema为4.033 hPa,Emr为0.395%,Erms为4.334 hPa。比较2种方法的Ema,Emr和Erms,显示出相同趋势,即OK法>IDW法,因此,IDW法对该区域的气压的插值效果更好。这与气压空间分布特征分析的结果一致[19]。

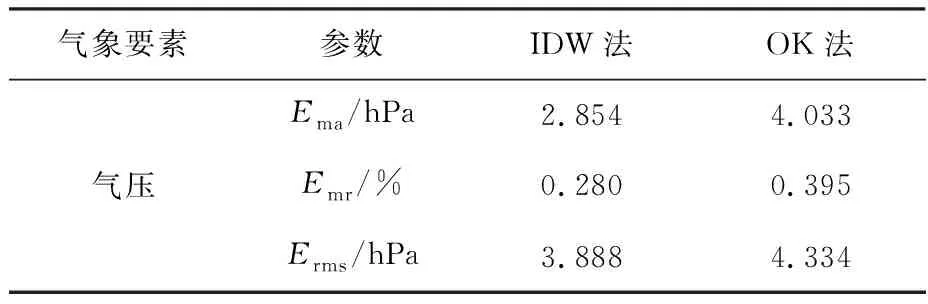
表6 气压的交叉验证结果

4 结束语

文章在不同幂指数的条件下,利用IDW法和OK法对气温、湿度、气压进行处理。在同一时间段与OK法进行比较,根据Ema,Emr,Erms的值比较插值精度。综合分析比较可知,相比OK法,IDW法的插值效果更好。幂指数分别为2,4,2时的反距离加权内插法是该小区域空间温度、湿度、气压的最优空间插值算法。

在插值过程中,采集点的气温、湿度、气压会受到周围采集点的数量、局部地区地形的影响,基于反距离加权内插法获得的气象要素分布图比普通克里金内插法获得的气象要素分布图更能准确、清晰地显示出校园气温、湿度、气压的分布。但是气象要素除了受经度与纬度的影响外,风速、风向、太阳辐射量等都会影响到监测数据。因此,随着数据密度的增加,不同插值方法的引入,有助于提高小区域的气象要素分布数据的准确性。