古代文明的数学智慧：文明古国乘法计算探析

池奕言

在各种文明的算术发展过程中，乘法计算的产生至关重要，它是人类从简单加减法的数学逻辑迈向复杂抽象计算的关键一步。整数、负数、有理数和实数的乘法都是由这个基本定义泛化而来的。（正数）乘法也可被视为在面积计算中对其边长给定的矩形区域的面积。

一个文明可以相对比较容易地发展出计数方法和加减法运算，但要想创造一套简单可行的乘法计算方法却不那么容易。中国古代计算用“算筹”不用笔，筹算可以改变形态横竖俱可，可以左至右运算。

筹算乘法分三层：上位是被乘数，中位是积，下位是乘数。先由乘数的最大一位去乘被乘数，再用第二位数去乘，两次之积对应位上的数相加，乘完为止[1]。如算49乘36的步骤，结果是1764。

使用的算筹计算看似简便，实际上这需要事先掌握九九乘法口诀表；考虑到古代文明的基础教育水平，这种计算并不完美。我国现代教育中使用的竖式乘法笔算方式也需要使用到九九乘法口诀表。

其他国家的乘法计算方式都一样吗？在数学的发展过程中，不同的文明创造出了哪些不同的乘法计算方法，其中有些计算方法甚至可以完全抛弃乘法口诀表（包括中国的计算方法）。

中国明代算书《指明算法》记载了中国的古代乘法计算方法，名字叫“铺地锦”，英文被称作“The Chinese method of multiplication”。李培业教授在《数学史研究》中认为“铺地锦”是我国自创的乘法计算方法。铺地锦歌诀为“写算铺地锦为奇，不用算盘数可知。法实相呼小九数，格行写数莫差池。记零十进于前位，逐位数数亦如之。照式画图代乘法，厘毫丝忽不须疑”[2，3]。

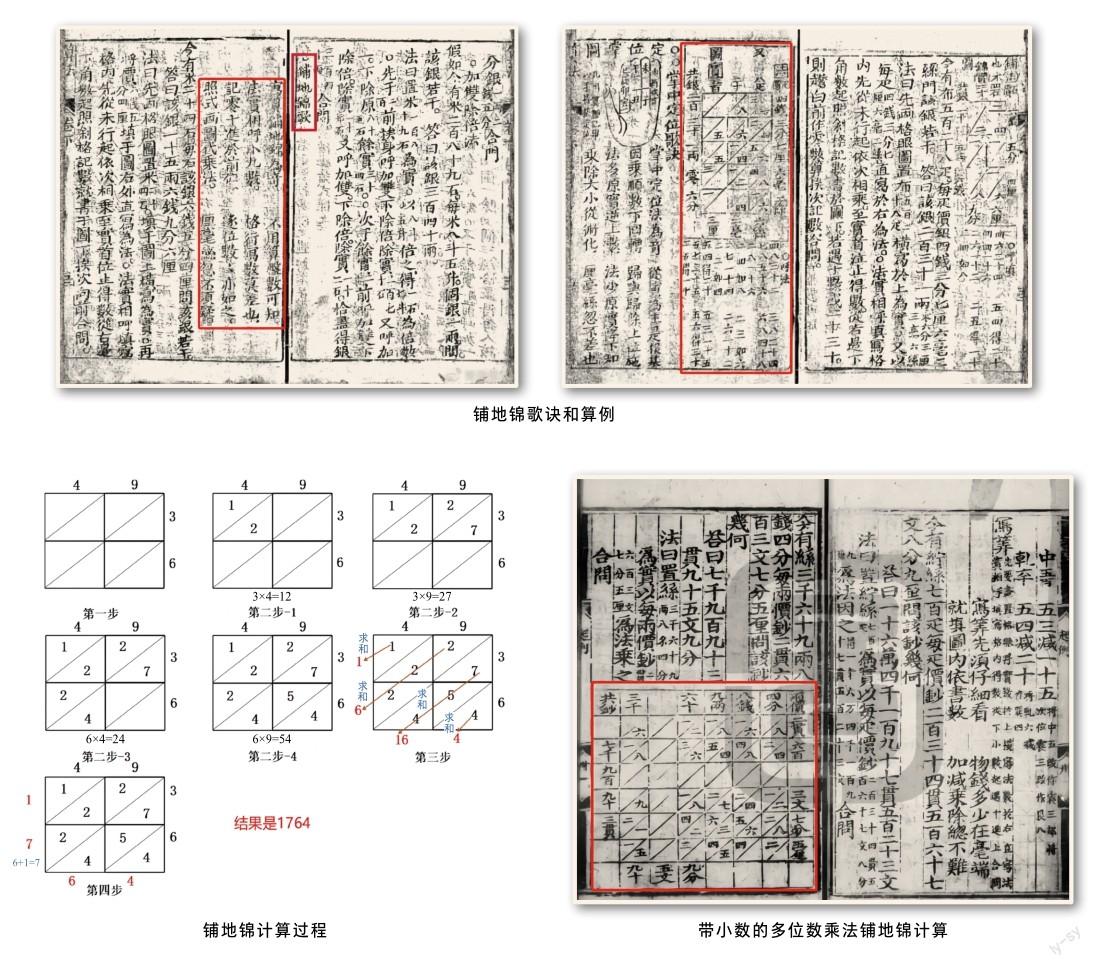
如果使用铺地锦方法计算49乘36的步骤，结果是1764。

计算步骤如下。

1.第一步：制作一个2×2的表格，使用反斜线将每个格子一分为二，把被乘数49写在格子图的上面，乘数36写在格子图的右面。

2.第二步：将上面的数字和右边的数字相乘，如左上的格子填写3×4=12（第二步-1）；同理分别填写好其他格子。

3.第三步：把表格中同一斜线里面的数全部加起来，写在格子图的左面和下面。

4.第四步：将进位的数字加到其左边或者上面的位数。

铺地锦计算方法虽然也需要掌握乘法口诀表，但是计算难度要比算筹法简单很多，而且比竖式法更加不容易出错。对于位数较多或者带小数数字的乘法计算也适用。

通过乘法分配率，“铺地锦”算法可以把复杂的多位值的乘法计算简化为个位数乘法和简单的加法计算，而乘法口诀表的普及使得个位数乘法相对容易，这种算法的思路和唐朝以来不断计算改革和简化计算，寻找和使用巧妙的计算方法思路是一脉相承的[4，5]。

众多周知，现在国际通用的阿拉伯数字是由古印度

人发明的。最早的印度数字出现在公元前2500年左右的哈拉帕文化中。公元733年，印度数字传入阿拉伯，阿拉伯人将其进行了改进，后来还将印度数字传入欧洲，当时欧洲人误认为这种数字是阿拉伯人发明的，称之为“阿拉伯数字”。

早在公元前2000年吠陀时期，印度人就对数学有很高的成就，当时希腊人能够表示最大的数字是10，而印度人可以表示到10。12世纪之后，印度人使用“格子乘法”，格子乘法的起源在哪里尚无定论，印度也许就是格子乘法的发源地[6]。

如果使用印度格子乘法计算49×36的步骤，结果是1764。

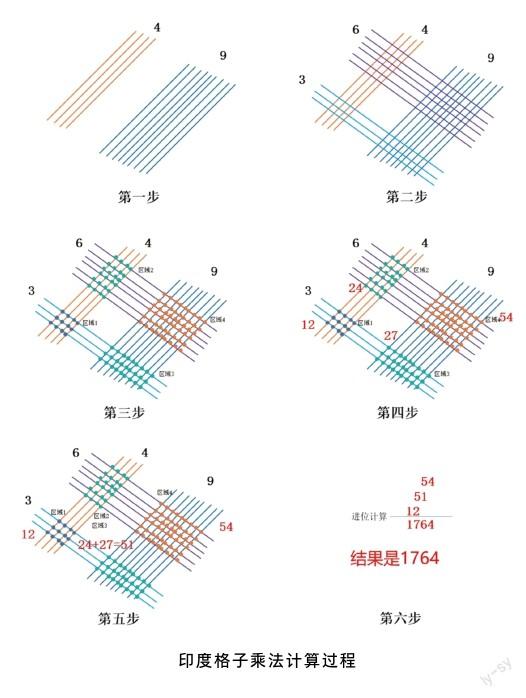
计算步骤如下。

1.第一步：把被乘数49分成两块线条；左边4条，右边9条。

2.第二步：把乘数36以垂直交叉方向分成两块线条，左边3条，右边6条。

3.第三步、第四步：計算4个区域的交叉点个数。

4.第五步：将区域2和区域3的数字相加。

5.第六步：从右往左进行进位相加。

印度格子乘法方法简单易懂，甚至不需要掌握乘法口诀表也可以使用，是一种适用文化程度较低的地区的简便方法，同时日本也在使用类似方式计算乘法。

九九乘法口诀表有着非常鲜明的递推规律：9×1=9，9×2=18，9×3=27，…，9×9=81。不难发现，随着乘数的递增，积的十位数字也依次递增，且比乘数减1，而个位数字依次递减，且积的两位数字之和都是9。举例乘数为5的乘法加以说明：9×5=（10-1）×5=50-5=45，不难看岀，积为50-5=45，其十位数字4一定比乘数减1，而个位数字5与乘数5之和为10，因此，积的两位数字之和恒为9。

印度对九九乘法口诀表进行了改进，升级为十九超级乘法表，可以大大缩减计算时间，超级乘法口诀表是从1到19[7]。

那么从11×11到19×19，印度人是怎样记忆超级乘法口诀的呢？把被乘数与乘数的个位数字加起来；将这一步的得数乘以10；把被乘数、乘数的个位数字乘起来；将前两步的得数加起来，所得的结果就是所求的积。

超级乘法口诀甚至可以将其升级为99×99的乘法口诀表，从21×21到29×29、31×31到39×39，…，91×91到99×99，也使用类似的算法。以63×65=4095加以说明：63×65=（63+5）×60+3×5=4080+15=4095。

古埃及的乘法运算不需要大量的口诀背诵，只要知道翻倍乘法就可以了，即乘2乘法。以11×16为例，对被乘数11不停乘以2（11×2，11×4，11×8，…）直至乘到数字16，得到结果176 [8]：

如果乘数不是2的幂，怎么计算呢？使用古埃及的乘法运算法计算49乘36为例。被乘数49翻倍，直到得出翻倍次数32，翻倍次数不要超过乘数，如果把32翻倍64就会超过36。同时因为36比32大，找出那些与32相加得36的翻倍次数，然后把翻倍次数相对应的数字相加（196和1568），得到结果1764。计算过程步骤如下。

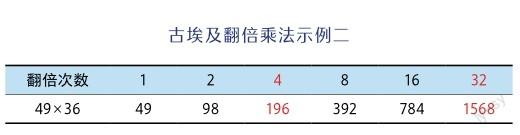
1.第一步：把被乘数49翻倍。

2.第二步：把乘数36拆分成翻倍次数之和36=32+4。

3.第三步：将对应的翻倍结果相加得196+1568=1764。

古埃及乘法不同于中国乘法计算，使用中国乘法计算的前提是必须掌握乘法口诀表，古埃及数学使用了类似二进制的乘法运算方法。古埃及人意识到任何一个数都可以表示为若干个不同的2的幂的和，这其实和计算机系统的二进制的计算是有着相同原理的[9，10]。

无独有偶，古代俄罗斯使用类似的一种乘法计算，将被乘数逐次减半，遇到奇数则减1后再减半，同时乘数依次加倍；找出所有奇数数字，其对应的数之和就是乘法结果。这个做法与古埃及的算术法相当类似，但看起来更奇特一些。使用俄罗斯的乘法运算法计算49乘36，计算过程如下表。

挑出减半后是奇数的数字（49，3和1），将其对应的数字相加即可（36+576+1152=1764）。

在古代的两河流域，人们使用粘土制成泥板，其上用楔形文字书写。现存有数以百计的两河数学文献在泥板上保存下来，这一时期已发展出成熟的数字体系。在古巴比伦的基础教育中，一个重要的组成部分是记忆大量倒数表（不是今天理解的倒数）和乘法表，同时需要依靠抄写来辅助记忆。从现有的泥板材料可以看出，学习算术有固定的次序和内容，构造倒数表是其中的一步，同样倒数表也可以用于乘法。

六十进制的使用为古巴比伦数学的乘法运算发展带来了很大的障碍，因为如果要背乘法口诀表的话，至少也得背一千多项。所以古巴比伦人利用表格代替乘法口诀表。这些计算有关的表格可能用于学习时的背诵，也可能用于实际的换算或计算，是古巴比伦人计算的重要辅助工具。

这块泥板给出了形如60/N的整数的六十进制展开，但是还未使用分数概念。其上的文字可释读为：

60的2分之一等于30；其3分之一等于20；其4分之一等于15；其5分之一等于12；其6分之一等于10；其7又1/2分之一等于 8；其8分之一等于7又30；其10減1分之一等于 6又40；其12分之一等于 5……

由于古巴比伦采用六十进制，这样的一个列表相当于倒数表。实际应用这些表格进行计算时是带计量单位的，这些六十进制数字本身没有绝对位值，也就是说乘积等于60的任何幂次的两个数就互为倒数。如第一行“60的2分之一等于30”，则2与30互为倒数，因2×30 =60。古巴比伦的倒数表里所有的数都是精确的小数，在六十进制中都是有限小数。需要计算乘法时，古巴比伦人就去查询表格从而得到结果，通过大量背诵和记录来避免乘法计算是古巴比伦的方法[10，11]。

碰到无限小数时，他们会用取近似值的方法来解决。例如，古巴比伦人会通过1/13=1×（1/13）=7×（1/91）≈7×（1/90）=7×（40/3600）=（7×40）/3600来计算1/13的值。那个40就是查倒数表查出来的。

乘法的计算方法体现了古人的数学智慧。一个乘法计算方式有如此多的方法，可见数学的魅力所在。在各种计算方法中，各国采用了不同的进制，中国、印度采用了十进制，古巴比伦采用了六十进制，古埃及采用的方式接近于二进制。

中国的“铺地锦”计算方法，虽然需要背诵乘法口诀表，但是其清晰的计算结构可以减少计算差错，同时也可以高效地用于计算多位数和小数，和我国常用的计算工具“算盘”计算方法的思路一脉相承。

印度采用的进制与我国相同，采用十进制，虽然画图较为麻烦，遇上8，9这样的大数画起来比较费时间；用于1，2这样的小数字，数起交叉点来还是比较简单的，而且因为不需要背诵乘法口诀表适用于教育程度较低的地区。同时，印度19超级乘法表能够节约大量的时间，也是一个很高效的计算方法。

古埃及采用的方式接近于二进制，古埃及人意识到任何一个数都可以表示为若干个不同的2的幂的和。这其实和计算机系统二进制的定义是如出一辙的。这个方法不用背诵也不需要画图，仅仅需要掌握乘2的简单乘法，乘2的计算方法又可以简化成加法，受到基础加减法算术教育的人民就可以进行乘法运算。

古巴比伦采用六十进制的方法，60过大很容易出错，为乘法运算发展带来了很大的障碍。但是古巴比伦对于无限小数和倒数的认知，为我们打开了数学新世界的大门。古巴比伦人把除以一个数看作是乘以它的倒数，利用查找倒数表可以很方便地实现乘除法的换算。这种方法将计算转化成查找，和现代数学中利用对数表计算异曲同工。

总之，各种算法各有优点，在那些充满聪明才智的古代文明頭脑中，总有意想不到的惊喜，为现在科技的快速发展做出了巨大的贡献。

（作者单位：温州第二高级中学）

[1]李红彦. 有趣的算筹. 数学小灵通（1-2年级版）， 2020（12）： 41-42.

[2]李林明. 古人怎样算乘法.数学小灵通（3-4年级版）， 2014（04）： 34， 35， 45.

[3]梅艳珍. 赏析古代乘法算式“铺地锦”. 教育实践与研究（A）， 2011（02）： 50-51.

[4]周全中. 铺地锦乘法的来龙去脉. 齐鲁珠坛， 2000（03）： 18-19.

[5]青華道人.举例说明西方“格子乘法”就是中国的“铺地锦”写算法. https：//weibo.com/ttarticle/p/show？id=2309404715295246778659

[6]王邵惠子. 古代印度算术理论研究. 辽宁师范大学学报， 2019.

[7]优博数学. 神奇的印度式乘法—古代数学智慧介绍. https：//baijiahao.baidu.com/s？id=1624184299783266665&wfr=spid er&for=pc

[8]裴庄. 古埃及人独创的乘法和除法. 中学生数学， 2002（06）： 40.

[9]phoenix890209. 知道古埃及人是怎么做乘法的么？https：//blog.csdn.net/phoenix890209/article/details/5272487

[10]Matrix67. 没有乘法口诀表将会怎样： 古巴比伦乘法和古埃及乘法. http：//www.matrix67.com/blog/archives/360？replytocom=6406

[11]顾森. 独特的古巴比伦数学. 中学生数理化（初中版） （中考版）， 2011（12）： 21.

关键词：乘法 古文明 计算方法 ■