水力压裂工况对活动弯头冲蚀行为的影响
2023-12-31高凯歌闫柯乐孙少光靳彦欣陈勇蒋秀
高凯歌 闫柯乐 孙少光 靳彦欣 陈勇 蒋秀
中国石化安全工程研究院有限公司
冲蚀是指含有固体颗粒的流体冲击设备而导致其表面材料损失的现象[1-4],是造成管道减薄、设备设施失效的重要原因之一[5-8]。活动弯头由于其结构简易、变换灵活的特点,广泛应用于在压裂过程中调整压裂液流动方向[9]。压裂过程中,压裂液携带固相支撑剂在高压管汇中高速流动。活动弯头作为转折结构,大量支撑剂与内壁撞击产生冲蚀效应,导致壁厚减薄,发生穿孔、爆裂的概率远高于直管、法兰、节流阀等其他高压管汇组件,故活动弯头平均寿命较低,极大地制约了压裂施工的连续性和安全性[10-11]。
活动弯头冲蚀是一个复杂的过程,与压裂液排量、流道结构、流体性质、含砂率、支撑剂尺寸等因素有关。因此,国内外学者基于流体动力学模拟对弯头冲蚀进行了大量研究[12-14],王凯等[15]提出相对冲蚀率概念,研究了特定流速下一定粒径的固相颗粒的冲蚀行为。张继信、成芳、周兰等[16-19]分别针对支撑剂尺寸、含砂率、压裂液流速、黏度等因素对弯头冲蚀的影响进行研究,并得到单因素影响规律。WANG 、涂亚东、彭文山等[20-23]分析了高压活动弯头曲率半径、通径及弯曲角度等结构参数对冲蚀规律的影响。上述研究多针对单弯弧的活动弯头进行,而在实际使用中,由于现场布局、安装条件的限制,活动弯头的弯弧数量及安装角度将发生变化[24-25]。为此,结合压裂现场工况和活动弯头的实际使用情况,利用CFD软件建立了不同安装角度的双弯弧活动弯头模型,研究了安装角度、支撑剂质量流量、压裂液流速及黏度等因素对活动弯头冲蚀的影响规律,并与现场实际失效弯头进行对比验证,为提高高压管汇的可靠性和安全寿命提供理论依据。
1 计算模型
1.1 连续相流动方程
分别选取连续方程、动量方程和标准k-ε湍流模型作为数值模拟的控制方程。
(1) 连续方程见式(1)。

(1)
式中:ρ为连续相密度,kg/m3;t为时间,s;u为连续相瞬时速度矢量,m/s。
(2) 动量方程见式(2)。
(2)
式中:p为液相内压力,Pa;μ为黏度,Pa·s;I为单位张量,无因次;g为重力加速度,m/s2;F为体积力,N。
(3) 湍流模型见式(3)。
(3)
式中:k为湍流动能,J;μi为沿切向的速度分量,m/s;μt为湍动黏度,Pa·s;Gk为由于平均速度梯度引起的湍动能k的产生项,无因次;ε为湍流耗散率,无因次;xi、xj为空间坐标,i和j取1,2,3,i≠j;σk为k方程的湍流Prandtl数,取1.0;σε为ε方程的湍流Prandtl数,取1.3;Sk、Sε为自定义参数,无因次;C1ε、C2ε、Cμ为经验常数,分别取1.44、1.92、0.09。
1.2 离散相控制方程
采用Lagrangian方程对颗粒轨迹进行求解,固体颗粒的受力方程见式(4)。
(4)
式中:up为沙粒速度,m/s;t为时间,s;FD为固相颗粒所受的拖曳力,N;u为液相速度矢量,m/s;up为固相颗粒速度矢量,m/s;FD(u-up)为颗粒单位质量上的拖曳力,N;ρp为沙粒密度,kg/m3;dp为沙粒直径,m;Rep为相对Reynolds数,无因次;gy为y方向重力加速度,m/s2;CD为曳力系数,无因次;Fy为y方向的其他作用力,N;a1、a2、a3为经验常数[26]。
1.3 冲刷腐蚀模型
活动弯头冲蚀主控因素包括固相颗粒速度、流量、尺寸、撞击角度、弯头内径等,本研究采用Huser和Kvernvold提出的颗粒碰撞角度函数模型[27]进行计算,见式(5)~式(7)。
(5)
f(θ)=2.69θ=1.61θ2-8.84θ3+7.33θ4-1.85θ5
(6)
C(dp)=1.8×10-9
(7)
式中:Rerosion为壁面冲蚀速率,kg/(m2·s);N为固相碰撞个数,无因次;mp为固相质量流量,kg/s;C(dp)为颗粒直径的函数;θ为颗粒撞击角度,(°);f(θ)为撞击角的函数;b(v)为相对速度的函数,取2.6;Aface为壁面计算单元的面积,m2。
1.4 避免碰撞恢复方程
固相颗粒撞击壁面会导致能量转移和损失,速度分量会在撞击后发生变化。通常以恢复系数(撞击前后速度分量的比值)衡量能量的损失情况。本文采用Grant和Tabakoff恢复系数进行计算,见式(8)。
(8)
式中:N和T分别代表切向和法向方向。
2 数值模拟
2.1 高压弯头计算模型
近年来,在压裂施工过程中因冲蚀导致刺漏、爆裂的位置主要集中在井口区域由地面向上的活动弯头处。选用通径为69.85 mm的“3″-1502长半径活动弯头”作为研究对象,并将模型进行简化。如图1所示,高压弯头模型主要由进口直管段(L1)、第一弯弧(R1)、弯弧连接段(L2)、第二弯弧(R2)和出口直管段(L3)5部分组成。为还原内部流动结构并使管内固液充分流动,图中L1、L2、L3的长度分别取700 mm、70 mm、1 400 mm,弯弧曲率半径为104.775 mm。
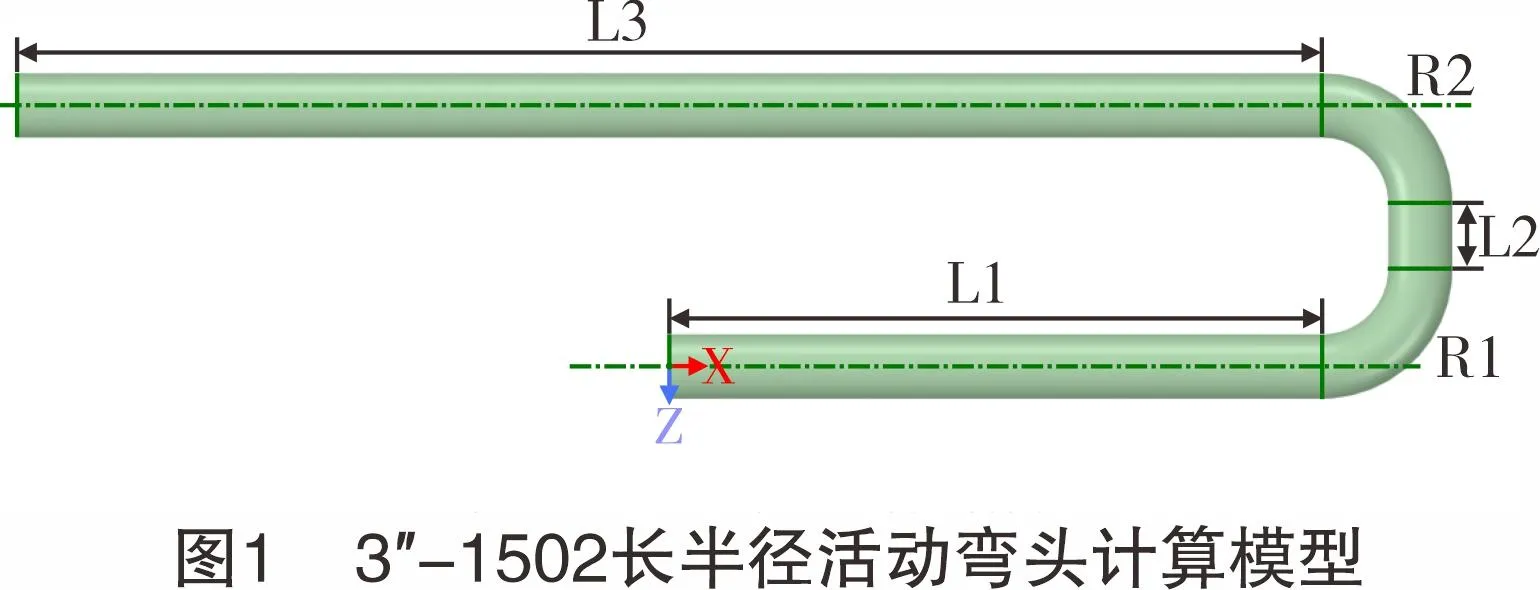
2.2 网格划分与边界条件
网格类型和尺寸决定了计算总量和精度。将计算流域按入口直管段、弯弧段、弯弧连接段、出口直管段进行六面体网格划分,并在弯弧段的壁面处将网格细化,使计算结果更加精确,网格边界层设置为20层。针对网格敏感性进行分析发现,在较少网格数目下,冲蚀速率随着网格数目的增多呈现波浪形不规则变化,当网格数超过2.6×105后,最大冲蚀磨损速率趋于稳定。
基于水力压裂井施工现场的实际工况参数,设置管段进口边界条件为速度进口,管壁为反射边界,重力方向沿y轴负方向。假设管段进口处支撑剂和携砂液的速度方向一致且初始速度相同,入口速度为8~20 m/s,出口压力为100 MPa,冲蚀介质为压裂液加支撑剂,离散相(支撑剂)粒径为270 μm,表观密度为3.5 g/cm3,压裂液中支撑剂质量流量为4.2~33.6 kg/s,压裂液的动力黏度为10~150 mPa·s。
3 结果与分析
根据现场实际,选取安装角度为75°的高压活动弯头作为计算对象,设定压裂液黏度为20 mPa·s,流量为12.2 m/s,支撑剂质量流量为12.6 kg/s,出口压力为100 MPa。高压活动弯头的冲蚀形态如图2所示,压裂液对活动弯头的冲蚀行为主要集中在第一弯弧外拱侧、第二弯弧外拱侧以及出口直管段,其中,以第二弯弧外拱侧出口位置的冲蚀磨损最为严重。
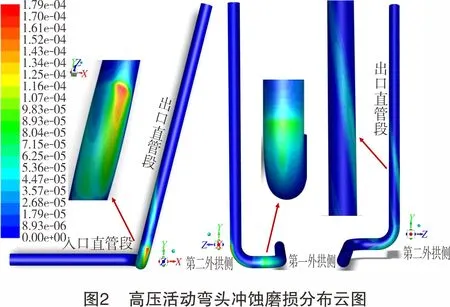
入口直管中,支撑剂在携砂液中具有较强的跟随性,流动轨迹与直管段轴向基本保持平行,几乎不与管壁发生碰撞。因此,管壁几乎不存在冲蚀现象。在第一弯弧处,由于离心力和惯性的共同作用,部分支撑剂偏离原有轨迹与外拱侧壁面发生碰撞,在第一弯弧外拱侧造成“T”字形冲蚀形态,最大冲蚀速率约为9.53×10-5kg/(m2·s)。第二弯弧段由于流道方向和纵向偏移角度(安装角度)同时发生变化,大量支撑剂在紊流、离心力、重力和惯性的共同作用下以较小冲击角撞击第二弯弧段的外拱侧内壁面,在整个第二外拱侧区域造成了严重的冲蚀磨损,冲蚀磨损最严重的区域为第二弯弧段出口处右颊,最大冲蚀速率约为1.79×10-4kg/(m2·s)。由于两相流体在双弯弧段形成了二次对称流,且连续流道变换加剧了二次流的紊乱程度,与轴向主流发生叠加作用后,弯弧出口直管段内的流体呈现出较为剧烈的“螺旋”流态,撞击直管内壁并造成直管段的“螺旋状”冲蚀形态。
3.1 安装角度对活动弯头冲蚀的影响
在施工过程中,需要根据场地布置改变活动弯头的安装角度(内部流场),进而导致冲蚀规律和形态差异。为研究不同安装角度对活动弯头冲蚀行为的影响,选取安装角度分别为30°、45°、60°、70°、75°、80°和85°的活动弯头作为研究对象。设定压裂液黏度为20 mPa·s、流速为12.2 m/s、支撑剂质量流量为12.6 kg/s,计算得到各部位的冲蚀速率和最大冲蚀磨损区域,结果如图3和图4所示。
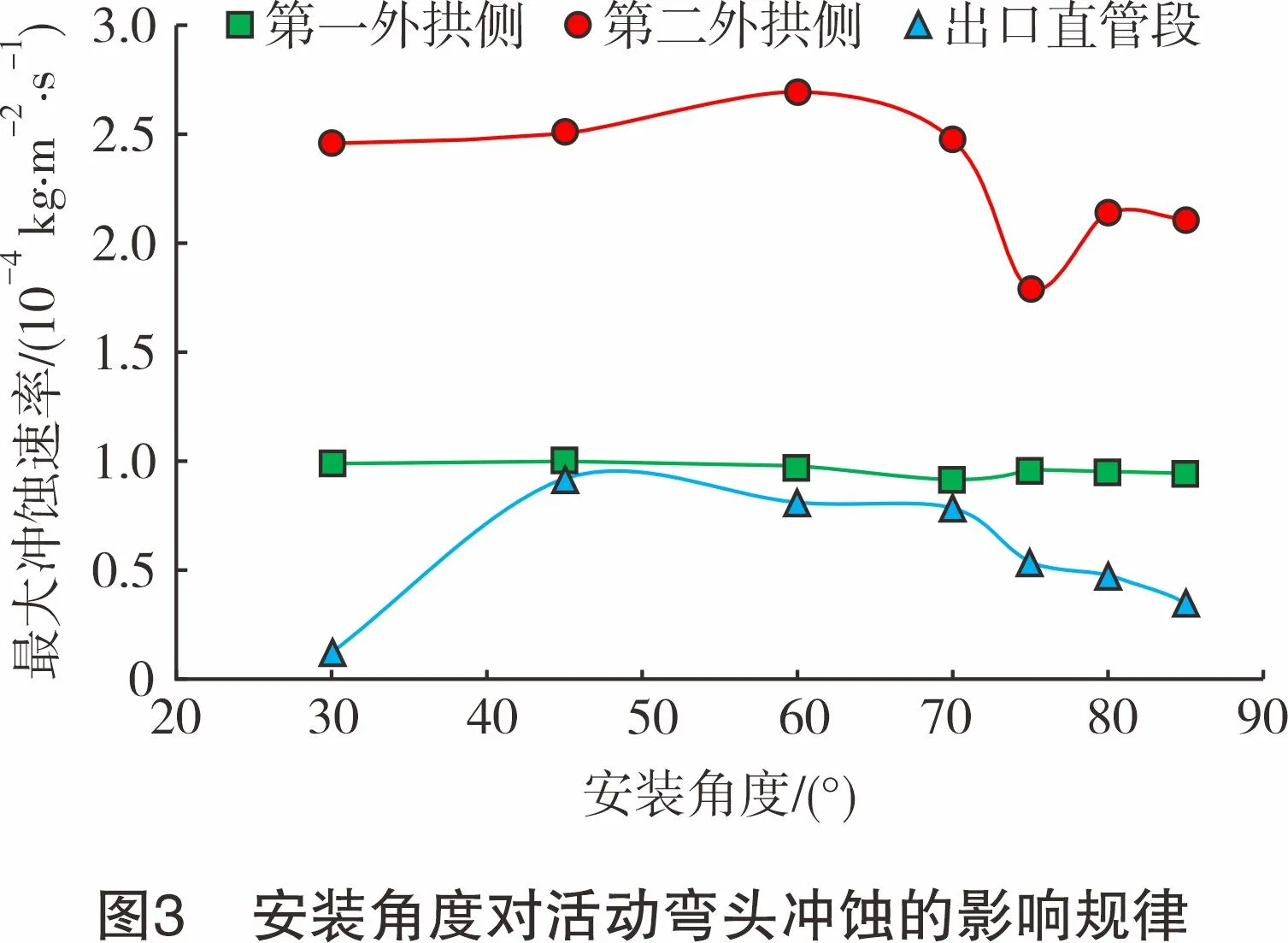

计算结果表明,不同安装角度下,活动弯头最严重的冲蚀区域均出现在第二弯弧出口位置的外拱侧,并偏向于弯弧轴向的右颊,冲蚀形态基本一致。30°~60°范围内,最大冲蚀速率呈缓慢上升趋势。当安装角度超过70°时,冲蚀速率迅速降低,在75°时出现极小值,80°和85°时的最大冲蚀速率相对于75°略有上升,但变化幅度不大。由于流道结构相同,活动弯头第一弯弧外拱侧最大冲蚀速率保持稳定。出口直管段的最大冲蚀速率先随着安装角度呈上升趋势,并在45°~50°之间达到峰值,之后随着安装角度的增大呈下降趋势。因此,在压裂施工现场应充分考虑场地布局,尽量选用安装角度超过70°的活动弯头向井口输送压裂液。
3.2 支撑剂质量流量对活动弯头冲蚀的影响
支撑剂质量流量是影响高压管汇冲蚀速率的主控因素之一。在实际压裂施工过程中,压裂液含砂量随着施工时间的延长呈阶梯式分布。选取安装角度为75°的活动弯头作为研究对象,在管流速度为12.2 m/s、出口压力为100 MPa的条件下,设定支撑剂质量流量分别为4.2 kg/s、8.4 kg/s、12.6 kg/s、16.8 kg/s、25.2 kg/s、33.6 kg/s,计算得到不同质量流量下对活动弯头的冲蚀速率,如图5所示。

由图5可知,随着活动弯头中支撑剂质量流量的增大,冲蚀区域分布未发生明显变化。但与壁面发生碰撞的支撑剂数量显著增加,导致高压管汇整体冲蚀强度随之增加,各部位最大冲蚀速率随质量流量的增大均呈线性增大。当质量流量为33.6 kg/s时,各部位冲蚀速率增速略有降低,这是因为质量流量过大导致支撑剂相互碰撞几率增加,颗粒间的相互碰撞、反弹产生“屏蔽效应”,从而降低支撑剂与内壁的撞击概率及能量。
3.3 压裂液流速对活动弯头冲蚀的影响
选取安装角度为75°的活动弯头作为研究对象,在支撑剂质量流量为12.6 kg/s、出口压力为100 MPa条件下,设定压裂液流速分别为8.0 m/s、10 .0m/s、12.2 m/s、15 .0m/s和20.0 m/s,得到不同流速对冲蚀行为的影响规律,结果如图6和图7所示。
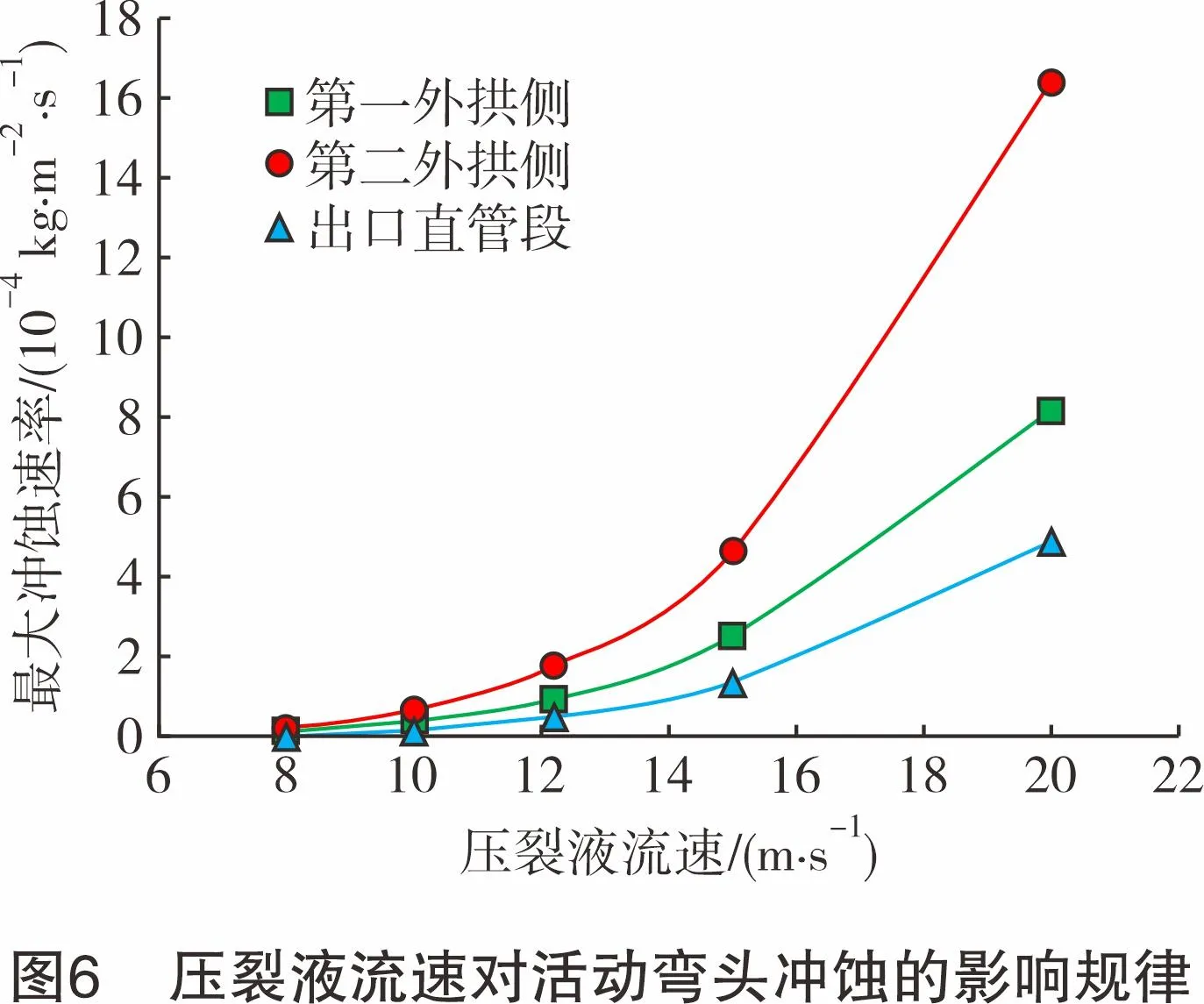

由图7可知,随着压裂液流速的增大,活动弯头冲蚀分布未发生明显变化,但冲蚀形态显著集中,且随着流速的不断增大,活动弯头各部位冲蚀速率呈现近指数级增大,最大冲蚀速率始终位于第二弯弧外拱侧的出口处。究其原因,是由于支撑剂在压裂液中有较强的跟随性,随着流速的增加,对支撑剂的携带能力显著提高,支撑剂在流体中由于重力或惯性所导致的离散现象减弱,与活动弯头内壁的撞击区域更加集中。同时,由于流体流速增大,固相支撑剂的速度也随之增大,支撑剂撞击活动弯头内壁时的切削、挤压效应及其所释放的能量也显著提高,最终导致冲蚀速率近指数级增大。
3.4 压裂液黏度对活动弯头冲蚀的影响
在压裂施工过程中,随着含砂率呈阶梯式增长,为保证压裂液的携砂能力,其黏度也逐步增大。选取安装角度为75°的活动弯头作为研究对象,在压裂液流速为12.2 m/s、支撑剂质量流量为12.6 kg/s、出口压力为100 MPa的条件下,设定压裂液黏度分别为10 mPa·s、20 mPa·s、30 mPa·s 、40 mPa·s、50 mPa·s、60 mPa·s、80 mPa·s、100 mPa·s、120 mPa·s和150 mPa·s,得到不同压裂液黏度对冲蚀行为的影响规律,结果见图8和图9。


如图8所示,在压裂液的黏度范围内,第一弯弧外拱侧的最大冲蚀速率随黏度的增加先逐渐降低,然后在约80 mPa·s后逐渐稳定,这是由于支撑剂密度高,单体质量大,在流体黏度较低的条件下,流体对支撑剂的黏附力较弱,导致颗粒在第一弯弧处受重力影响大,较多支撑剂冲破压裂液的黏附效应与管壁进行碰撞造成冲蚀。随着流体黏度的增大,对支撑剂的黏附力也逐渐增大,支撑剂的跟随性逐渐加强,离心力的作用效果降低,对管壁碰撞的概率降低,冲蚀速率相应减小。当黏度在10~40 mPa·s范围内时,第二弯弧外拱侧的最大冲蚀速率较为稳定,随着携砂液黏度的增加,冲蚀速率逐渐增加,并在120 mPa·s后趋于平稳。这是由于第二弯弧处的压裂液紊流程度远大于第一弯弧处,在低黏度条件下支撑剂由于液相黏滞力、重力、离心力等多重作用导致轨迹相对混乱,相互碰撞的概率较高,随着携砂液黏度的增加,携砂液的黏附效应增大,支撑剂的跟随性和速度均有所提高,随压裂液主流流向与管壁碰撞的数量和速度增加,冲蚀速率也随之提高,当携砂液黏度超过临界值后,第二弯弧外拱侧的冲蚀速率也保持稳定。
如图9所示,在低黏度条件下(10~30 mPa·s)第二弯弧的冲蚀严重区域主要分布于弯弧出口右颊。随着压裂液黏度的增加,冲蚀危险区域逐渐向弯弧中部和左颊的方向偏移,且高冲蚀速率区域先逐渐缩小,随后趋于稳定。这是由于随着压裂液黏度的增加,对支撑剂的黏附力提高,在流道变化位置支撑剂本身的惯性效应下降,对压裂液的跟随性提高,突破压裂液黏滞效应继续前进或发散的支撑剂数量减少,绝大部分支撑剂随携砂液主流流向对管壁进行高速碰撞,导致冲蚀速率提高,同时造成冲蚀危险区域向后、向左偏移且更加集中。
3.5 数值分析结果与现场实际对比
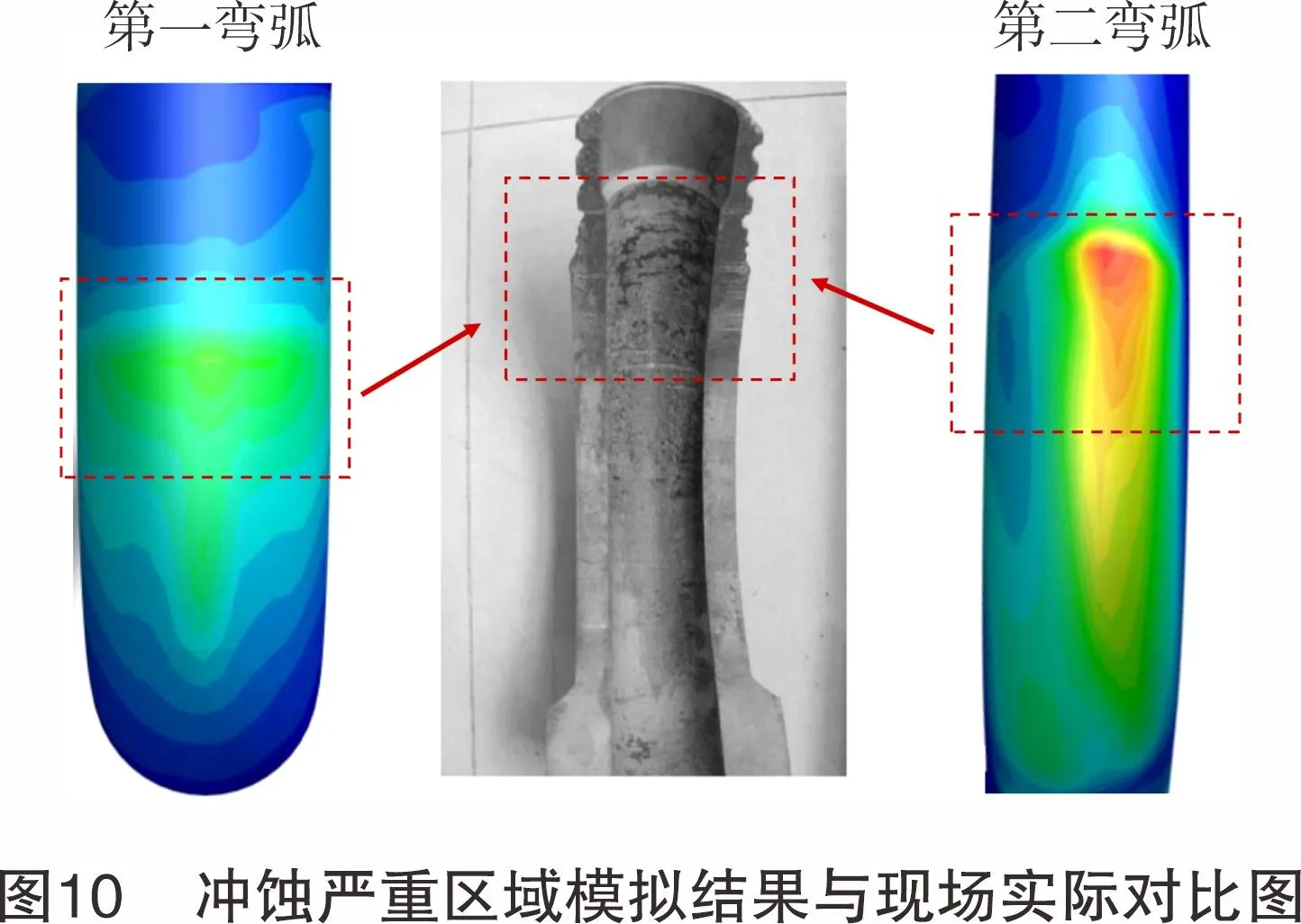
活动弯头冲蚀严重区域模拟结果与现场实际对比如图10所示[14],在压裂现场截取的失效高压活动弯头内壁面的冲蚀主要分布于弯头外拱侧,且出口处的冲蚀明显强于其他部位,在弯头入口几乎没有冲蚀发生,与模拟结果较为吻合。
4 结论
(1) 随着安装角度、携砂液流速、支撑剂质量流量的变化,双弯弧活动弯头的冲蚀形态不发生明显变化,最大冲蚀速率均出现在第二弯弧出口处外拱面;但随着压裂液黏度的增加,冲蚀危险区域逐渐由弯弧出口右颊向弯弧中部和左颊的方向偏移,且高冲蚀速率区域先逐渐缩小,随后趋于稳定。
(2) 双弯弧活动弯头安装角度在30°~60°范围内,最大冲蚀速率呈缓慢上升趋势。当安装角度超过70°时,冲蚀速率迅速降低,在75°时出现极小值,80°和85°时的最大冲蚀速率相对于75°略有上升,但变化幅度不大。压裂现场在保证施工要求的情况下,应尽量选用安装角度超过75°的活动弯头向井口输送压裂液。
(3) 当其他参数一定时,质量流量在4.2~25.2 kg/s范围内,最大冲蚀速率随着支撑剂质量流量的增大均呈线性增大;当支撑剂质量流量为33.6 kg/s时,冲蚀速率增速较之前略有降低。这是由于含砂率过大导致固相支撑剂相互碰撞几率增加,颗粒间的相互碰撞、反弹产生“屏蔽效应”。
(4) 活动弯头冲蚀速率随着压裂液流速的增大呈近似指数型增长趋势,但冲蚀分布未发生明显变化;压裂液黏度在10~40 mPa·s范围内时,活动弯头最大冲蚀速率较为平稳,随着黏度的逐渐增大,最大冲蚀速率也随之增大,并在120 mPa·s后趋于平稳。
