拟静力法地下通道抗震验算

沈中治

北京市市政工程设计研究总院有限公司 100082

引言

由于地下通道地震作用可借鉴的算例很少，工程设计人员容易产生疑惑，本文借编制标准图集的机会，对此作了探讨。主要问题有两个，一个是地下通道在地震力作用下的计算；二是通道在设防地震作用下的结构受力状态。

1 框架的内力和变形计算

1.1 计算思路

（1）根据力独立作用原理，将结构荷载分为水平荷载和竖直荷载两大类，对每种荷载分别作用计算结果进行叠加，即可得到结构总的内力和变形。

（2）水平荷载作用包括框架地震力、填土地震力、土压力、动土压力、土弹性抗力，共分三步：

第一步是求出框架整体内力，先将全部水平荷载化成框架节点力。由于水平荷载不对称，而框架是对称的，故产生的内力和变形都不对称。用“修正侧移刚度法”［1］计算出框架的整体位移和内力，具体步骤是：节点荷载——侧移刚度——侧墙水平位移——侧墙剪力——侧墙、顶板、底板的整体弯矩。

第二步是求框架的单体内力，由于结构已经完成侧向变形，每个单体构件（侧墙、顶板、底板）都按固端梁考虑。在固端节点处，相邻构件单体内力是平衡的，所以不管构件上是否有水平荷载，固端弯矩都是可以求取的。

第三步是将整体和单体内力叠加，即得到水平荷载作用下的内力。

（3）竖直荷载作用包括框架重力、填土重、铺装重，由于荷载对称、结构对称，故框架内力和变形都对称。节点无侧向位移，框架顶板、侧墙按闭合框架计算内力［3］，底板按弹性地基固端梁计算内力和变形［4］。

（4）将水平荷载和竖直荷载作用计算结果叠加，即得到框架的总内力和总变形。

（5）按各构件的配筋量进行强度验算。

1.2 内力和变形计算

通道尺寸如图1 所示。

本图集涉及的通道抗震设防类别为B类，设防烈度Ⅷ度地区，故只考虑水平向地震作用，不考虑竖向地震作用。

通道按纵向1m宽的框架计算。

1.水平荷载作用用“修正刚度位移法”，求框架整体位移和内力。（1）水平节点力由水平力求取（图2），框架侧移是顶板相对底板而言，故只需求取顶板A、C的节点力QA、QC。

图2 框架节点力Fig.2 Frame node forces

左侧墙地震力及土压力、动土压力，根据规范［2］可得：

左右侧墙顶板地震力和填土地震力。框架顶板上填土，地震力作用力小于土和顶板之间的摩阻力，所以填土的地震作用力传达到顶板上，加上顶板地震力总和T为：

右侧墙墙背土抗力：在地震作用下，框架顶板相对于底板发生变位，因侧墙后的被动土压力较大，大于土的抗力（安全系数2），所以墙后产生侧向水平抗力，抗力大小和位移有关，和深度呈正比，抗力系数。侧墙变形曲线按上下端固结梁考虑，水平位移为侧墙顶水平位移（m）（此值根据节点力和侧墙修正刚度求取）。水平抗力

当墙顶取单位位移时，侧墙顶刚度为：

框架总节点力：

式中：h、h1、d1、d2、L、b见图1 所示；Ci、Cs、A、γ、ϕ见规范［2］；m为填土水平抗力比例系数（kN／m4）；γδ为框架钢筋混凝土重度（kN／m3）。

（2）水平位移和水平剪力。顶底板和侧墙的刚度为i板＝EδI板／h，i墙＝EδI墙／L（I为惯性矩），由于节点产生转动，降低墙的抗侧移性能，故应予修正，根据顶底板和侧墙的线刚度比i墙，则刚度修正系数

侧墙顶的水平力，按刚度大小分配：

（3）框架整体构件的弯矩M′。侧墙反弯点高度位置和板墙线刚度比有关，可按从表1 查得反弯矩点系数y0。

表1 反弯矩点系数Tab.1 Coefficient of inflection point

（4）框架单体构件的弯矩M″。由于框架在总体节点力下完成节点的位移和转角，于是单体构件作为一固端梁，作用在上面的水平荷载产生局部弯矩，称之单体构件弯矩。

左侧墙弯矩：水平荷载为梯形，qA、qB作用。

右侧墙弯矩：水平荷载为矩形qC，和高次方程曲线作用。梁上弯矩先根据固端弯矩M″墙C和M″墙D的内插值，再叠加以按简支梁的弯矩M″简支x，可得：

式中：M″简支x为简支梁弯矩，可用简支梁上均布荷载qC的弯矩和集中力弯矩Mf公式积分后相加可得，如图3 所示。

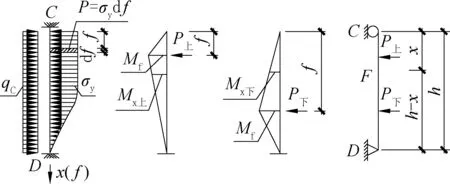
图3 右侧墙水平荷载按简支梁力系Fig.3 Horizontal load on the right wall according to the simply supported beam force system

当P在x以上时；

顶板、底板弯矩：

2.竖直荷载作用

框架结构图式为弹性地基上的闭合框架（图4）。

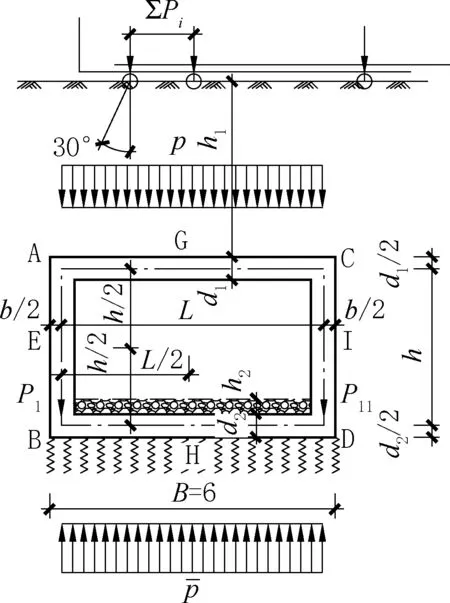
图4 框架竖直荷载Fig.4 Vertical load on frame

（1）顶板、侧墙及底板的荷载

顶面均布荷载（顶板、填土、车辆）：

底面均布荷载（底板、铺装）：

侧墙集中荷载：

式中：∑Pi为不利车辆位置轮重之和（kN）；∑S纵、∑S横为车辆纵横向距离之和（m）；γ铺装为铺装容重（kN／m3）。

（2）顶板、侧墙弯矩［3］

（3）底板按弹性地基梁

根据文克尔假定，地基反力和沉降成正比，由材料力学推算出梁受弯微分方程式：

解此微分方程，分别得到梁的内力和变形，即：挠度y，转角θ ＝y′，弯矩剪力Q＝反框架底板为两端固结的弹性地基梁，图集中梁长为：L＝5.5m～8.8m，因L＜3／β，故为短梁。由于没有短梁的计算公式，故选取了半无限长梁公式近似计算，半无限长梁远端边界条件和短梁不同，利用结构对称与荷载对称等条件，将公式中远端内力和变形进行局部修正。短梁左右两端承受上面传来的荷载，可分别用左右端为原点的两根反方向的半无限长梁替代在左右端点原点上作用此荷载来计算内力和变形，再将各种荷载计算结果叠加，得到总的内力和变形（图5）。

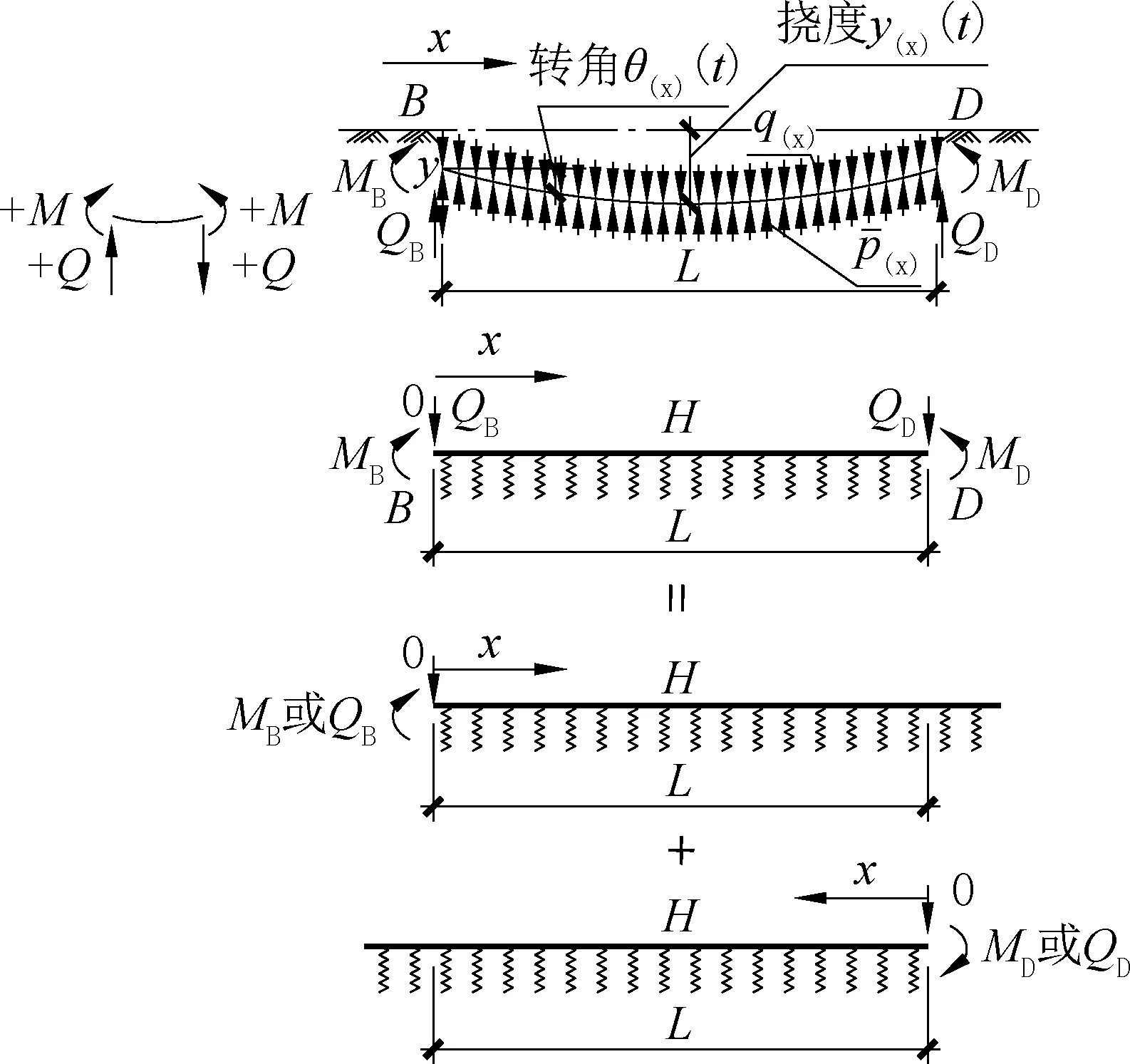
图5 弹性地基短梁化为半无限长梁作用Fig.5 Effect of transforming short beams on elastic foundation into semi-infinite beams

（4）底板内力和变形计算

框架底板在弹性地基上受到水平荷载和竖直荷载的作用，归纳起来，一共有四种承载型式，即：

Ⅰ.框架水平荷载产生的侧墙底弯矩MB、MD（图6a）；

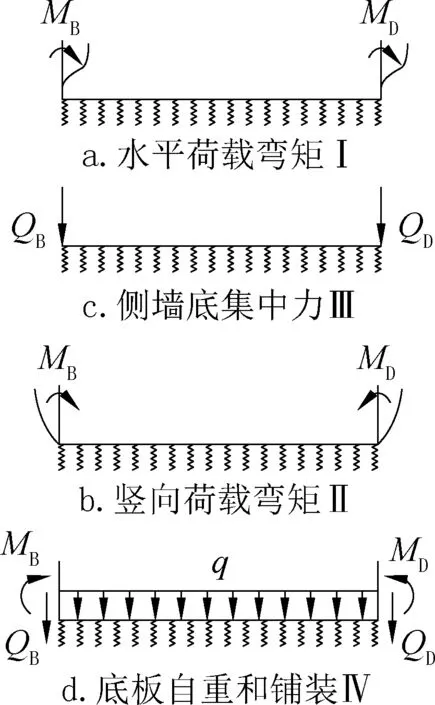
图6 底板在弹性地基上的承载型式Fig.6 Bearing type of bottom plate on elastic foundation

Ⅱ.框架顶板竖直荷载产生的侧墙底弯矩MB、MD（图6b）；

Ⅲ.侧墙底集中反力产生的剪力-QB＝QD＝（图6c）；

Ⅳ.底板自重及铺装均布荷载产生的梁端弯矩和剪力（图6d）：

式中：L为梁的长度（m）；x为梁的计算截面离原点的坐标值（m）；βx为梁的计算截面离原点的计算距离，β0、βL／2、βL分别表示梁的左端B、中点H和右端D的位置。

1.3 承载力计算

（1）材料：混凝土强度等级，钢筋种类，配筋量，地基物理力学性能。

（2）内力组合：根据JTG／T 2231-01 3.6 取地震作用E2、E1组合设计值。

（3）承载力验算：对框架顶板、侧墙、底板各控制截面及底面应力进行验算，按照公路桥梁设计规范JTG 3362—2018、地基基础规范JTG D63—2017 规定，采用钢筋混凝土偏心受压，斜截面抗剪，基础底面偏心受压等公式计算（或查阅计算图表［5］）满足且符合公路（城市）桥梁抗震规范JTG／T 2231-01—2020（CJJ 166）的要求。

2 计算实例

从图集中选取常规的断面，覆土较厚，设计条件有代表性的通道进行验算。

2.1 基本资料

（1）断面尺寸：净空5.0m ×2.50m（图1），d1＝d2＝b＝0.50m，h1＝2.50m，h2＝0.30m，h＝3.30m，L＝5.50m，B＝6.00m。

（2）材料参数：C30 混凝土，钢筋HRB400，钢筋混凝土弹性模量E＝0.8Ec＝2.4 ×107kN／m2，容重γδ＝25kN／m3，铺装容重γ铺装＝20kN／m3。

（3）地基：粉细砂土，场地类别Ⅱ类；场地基床系数κ ＝3.0 ×104kN／m3，承载力基本容许值［fA0］＝150kN／m2，填土水平弹性抗力系数m＝2.0 ×104kN／m4，容重γ ＝18kN／m3，内摩擦角ϕ ＝35°。

（4）抗震基本要求［1］

设防列度：8 度（A＝0.20g），设防分类：C类，设防目标：按两水准设防E1和E2，重要性系数：E1作用Ci＝0.34，E2作用Ci＝1.0。

2.2 内力和变形计算

地震作用E1、E2，为简明阅读，本算例中均采用E2表达（E1将最后补充结果）。

1.水平荷载作用（图2）

（1）框架节点力QA、QC

左侧墙地震力和地震土压力由式（1）～式（5）中代入Ci、Cs、A、γδ、b、ϕ等数据得：

qA＝19.82kN／m，qB＝46.14kN／m，QA1＝47.18kN

右侧墙地震力：

顶板地震力和填土地震力：

右侧墙土抗力：

总节点力：

（2）墙顶水平位移Δ和水平剪力VA、VC

在式（6）～式（7）中求得：

顶底板和侧墙的刚度：

顶底板和侧墙线刚度比：

左右侧墙侧移刚度：

水平位移：

水平剪力：

（3）框架整体构件的弯矩M′

（4）框架单体构件的弯矩M″

将前面已知的系数代入式（9）～式（11）中，计算出侧墙和顶底板的单体弯矩：

2.竖直荷载作用（图4）

由式（12）～式（14）中代入∑Pi＝2 ×2 ×140kN，∑S纵＝1.40m，∑S横＝1.3 ＋2 ×1.8m及前面已知的其他系数后，可得：顶面均布荷载p＝74.4kN／m，底面均布荷载q＝14.5kN／m，侧墙集中荷载P1＝35.0kN，继而再求出顶板、侧墙、底板的内力变形等。

（1）顶板、侧墙弯矩

（2）底板内力和变形

底板是弹性地基梁，共有四种承载型式（图6），本算例仅显示第Ⅰ种承载型式（其他承载型式后面补充结果）。

如图7 所示：

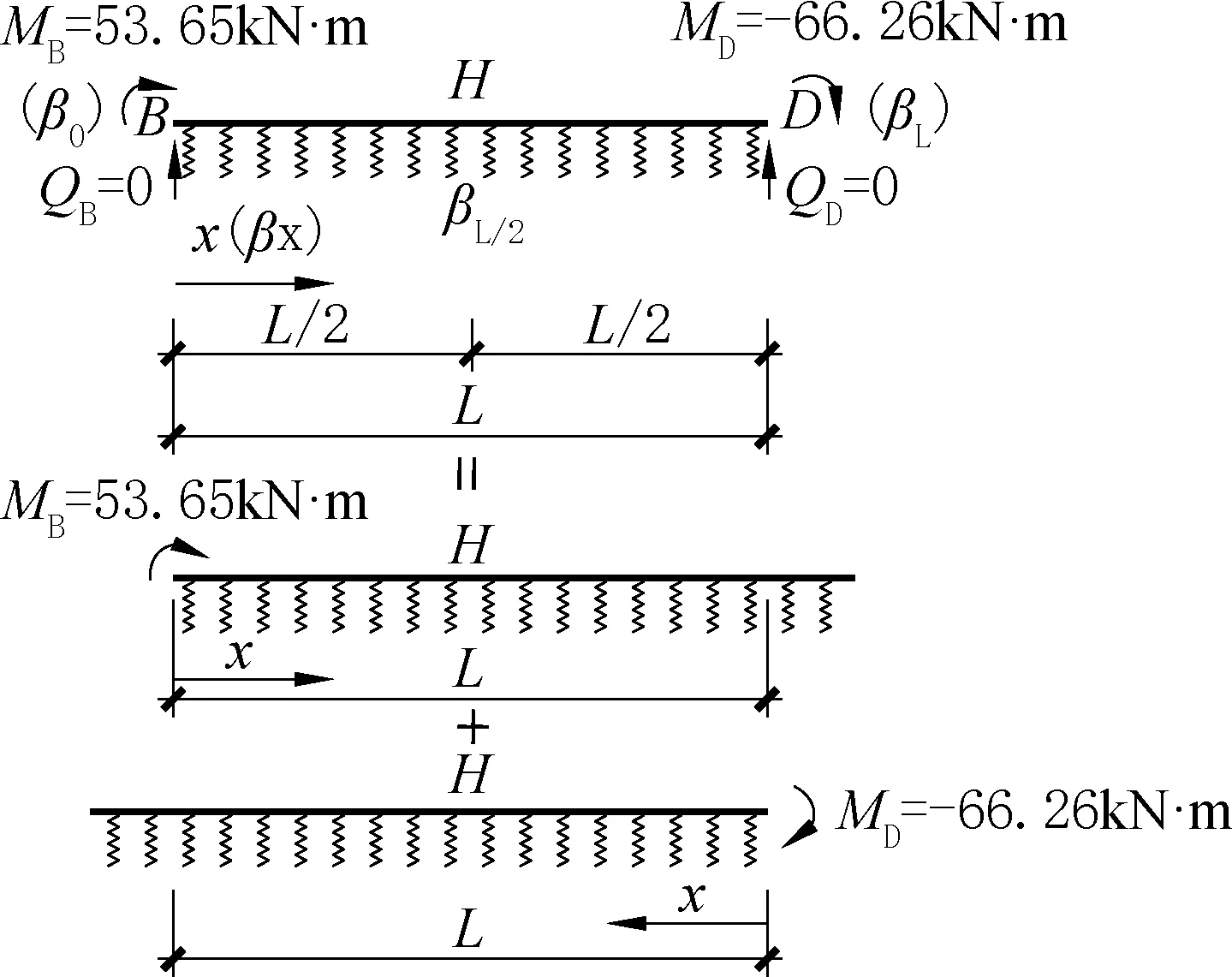
图7 底板在弹性地基上化为半无限长梁后按Ⅰ类承载作用Fig.7 The bottom plate is transformed into a semi-infinite beam on an elastic foundation and subjected to class Ⅰbearing action

图8 框架弯矩（单位：kN·m）Fig.8 Frame bending moment（unit：kN·m）

现分别对底板左端B、中点H和右端D截面所在位置β0、βL／2、βL，根据式（14）计算内力和变形。

挠度：

在计算了四种承载型式荷载后，底板的内力和变形如表2 所示。

表2 底板内力和变形Tab.2 Internal force and deformation of bottom plate

3.框架弯矩图

2.3 承载力验算

根据1.3（3）节的要求，框架承载力验算都能满足，如表3 所示。

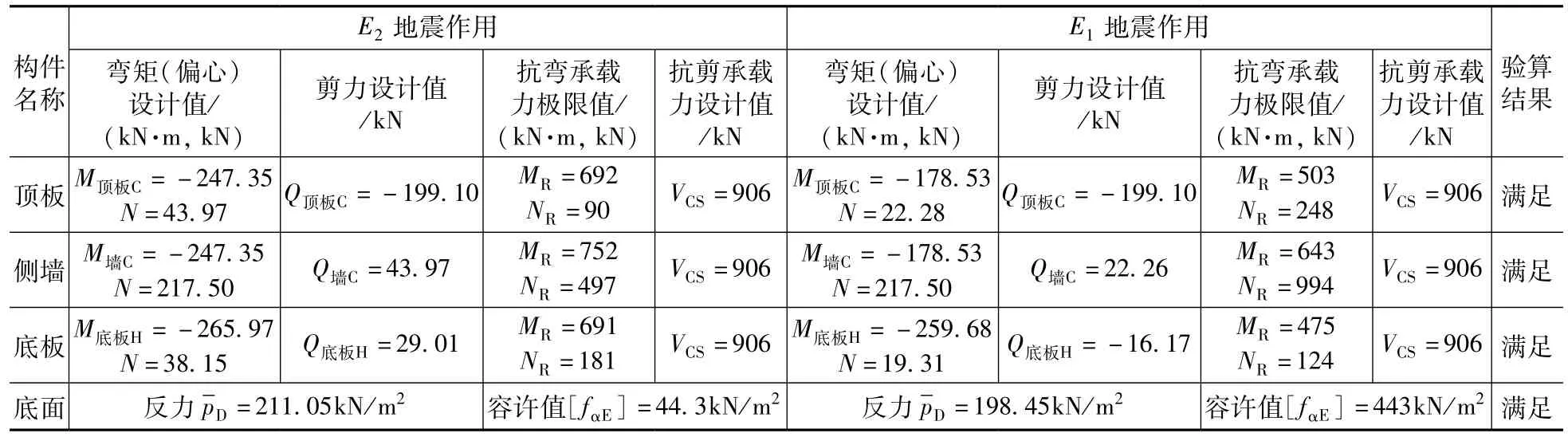
表3 框架地震承载力验算Tab.3 Checking calculation of seismic bearing capacity of frames

3 结论

1.按照上述思路，在选取了计算图式并在荷载取值及荷载作用方式确定之后，宜采用计算机软件（平面杆系程序）进行具体计算，这样可以快捷地得到满意的结果，本文采用解析方法，根据现有理论公式［2-5］，并经推导补充后完成，其优点是思路清晰，概念明确，且能满足工程精度要求，但是过于累赘。

2.框架地震荷载计算中，应该考虑顶板面填土的作用，以及墙背面水平弹性土抗力的作用，其作用方式前者为顶板上的均布静力，后者为沿侧墙高度呈高次方程的曲线分布。

3.对于常规的通道设计（材料：C30 混凝土，HRB400 钢筋，μ ＝0.7%配筋率）可以满足8 度地震作用，以此表明国标图集适用范围为基本烈度8 度的地震区。

4.通过计算，可以给设计提供如下资料：1）框架内力控制截面位置在顶板的端支点和底板中点，按常规的配筋，8 度地震时还有较富余的承载能力（本算例为40%）；2）框架变形量，在地震作用下，在土体不发生震陷、液化、弱化的条件下，其弹性变形量数值也不大（本算例水平为0.16cm，竖直为0.7cm）；3）框架顶板和底板在支点角隅处加腋是有利于抗震的。

5.通道是一个闭合框架结构，本文按静力法计算，鉴于框架顶板上集中了较大的静载，相对于侧墙，可视为单质点体系，根据反应谱理论，也可以采用伪静力法计算，即：等效单质点体系水平地震作用和底面总剪力相等且沿高度呈倒三角形分布，求出内力和变形，提出此方法，可供讨论。

编制“通道抗震”算例，前无可参仿之作，今笔者构思此文，乃是抛砖引玉之举，内中不妥之处，望同行批评指正！