基于BP神经网络和遗传算法的平面钢闸门优化设计

白凤玲,施文伟,包振东*

(1.南京市水利规划设计院股份有限公司,南京 210014;2.青阳县农田水利规划建设服务中心,安徽 池州 242800)

0 引言

金属结构闸门是水利工程中控制过流的重要设备,闸门在工程建设资金中占比较大,可达20%～50%[1]。在实际工程设计中,平面钢闸门的设计参数繁多,设计人员通常凭借设计经验进行判断,寻找合理的参数组合。这样设计结果的优劣往往取决于设计人员经验的丰富程度,也很难在兼顾结构强度的同时使闸门门重达到最优[2]。闸门结构优化一直以来都是困扰设计人员的一大问题。张淑琴等[3]采用APDL对叉梯式景观闸门进行了门叶结构的优化,实现与ANSYS软件的交互优化结构;章昕等[4]对弧形闸门的结构进行优化,采用VB语言完成退火遗传算法功能实现,并以此为基础进行了系统开发;宿爱香等[5]采用BP神经网络与遗传算法结合的形式对门式起重机主梁结构进行优化研究;郑圣义等[6]基于有限元算法对钢闸门主梁结构型式进行优化研究;冯锐[7]基于Inventor平台进行了平面钢闸门参数化建模的实用性研究,将BIM技术与闸门参数化优化进行结合应用;王军等[8]基于遗传算法对水工钢闸门参数化优化设计进行研究,采用12种参数表达闸门构造;董现等[9]应用遗传算法对神经网络结构进行优化,分析锈蚀削弱对闸门结构的影响。结合设计优化理论和计算机技术,对闸门进行结构优化,降低门重减少造价,开发针对平面钢闸门的辅助设计系统,将繁杂重复的工作交予计算机处理。提高设计工作中的“自动化”程度,减少设计人员重复劳动,对提高设计效率,减少工程造价具有一定意义。

1 平面钢闸门优化设计数学模型

平面钢闸门是由可以平动(或旋转)的闸门总成、水工建筑物中的预埋构件和控制闸门位置的动力设备等三个主要部分所组成。而闸门总成由门叶结构、行走支撑、止水等三部分组成。其中门叶结构是最主要的承力结构,又可分面板、梁格、空间联结系、吊具等构件。

设计中水位条件决定了闸门受到的水压力总和,是闸门设计中的最重要的影响因素。根据规范要求需保证材料强度符合要求,并保证整体及局部的结构稳定。为保证材料强度满足要求需要验算面板正应力、主梁翼缘正应力、主梁切应力、主梁最大挠度、边梁折算应力;为保证结构稳定需验算主梁、边梁板件厚度,截面稳定等。

1.1 数学模型的确定

设计中闸门门重G是影响闸门造价的主要因素[8],可以表示为密度、体积与重力加速度的乘积即G=ρgV。其中体积V又是由闸门设计参数构成的函数,设计中影响到闸门门重,以及与约束条件相关的主要设计参数,包括面板各参数XM、主横梁各参数XH、纵梁各参数XZ、次梁各参数XC、边梁各参数XB、滚轮位置参数XG。

根据闸门设计过程及设计优化理论思想,将闸门设计优化过程抽象为目标函数、设计变量、约束条件三个部分,其间关系可表示为:

(1)

1.2 设计变量

设计变量分为环境变量和待优化变量,环境变量为水工建筑物提供的结构需求包括水位条件以及孔口设计尺寸;待优化变量涉及闸门各部位近百项设计参数,可分为结构布置和截面尺寸两类。分析影响闸门设计的关键性参数对待优化变量进行简化,简化后闸门设计变量参数如表1所示。

表1 简化后闸门设计变量参数

1.3 目标函数

闸门自重G是影响闸门造价的重要因素,与闸门体积V正相关。因此可将闸门体积V最小定义为闸门目标函数,根据简化后设计变量具体可以表示为:

V=K高K宽Mt+5K宽[(Ht-Mt-Hyt)Hft+HybHyt]+2K高[(Ht-Mt-Hyt)Bft+BybByt]+3K高[(Ht-Mt-Hyt)Hft+0.8HybHyt]+V′

(2)

式中,V′为次梁及空间连接系总重,根据主梁间距确认次梁数n及槽钢截面积A后计算:

(3)

1.4 约束条件

闸门约束条件,一类是设计规范[10-11]中的强制性结构约束,如最小底缘角,面板最小厚度等;另一类是对结构的强度,刚度,稳定,震动频率等的限制。

主梁和边梁是闸门的主要承力结构,也是应力集中区,其主要约束包括:

(1)面板正应力、主梁翼缘侧正应力:

[σ]≤255 MPa

(4)

(2)主梁切应力:

[τ]≤135 MPa

(5)

(3)主梁挠度:

[η]≤1/600K宽

(6)

(4)主梁长细比:

120Hft≤Bt

(7)

(5)边梁稳定:

3(Bt-Ht)≤X2

(8)

(6)边梁最大折算应力:

σ≤1.1[σ]≤247.5 MPa

(9)

(7)闸门整体结构稳定:

K高/3≤GL1

(10)

(8)闸门整体支撑稳定:

(11)

(9)滚轮稳定:

GL2≥0.5Ga

(12)

(10)最小底缘角:

(13)

2 基于BP神经网络的闸门受力分析

工程设计中需对强度、刚度进行计算校核,多参照规范提供的平面分析方法,计算结果偏保守。使用有限元法对闸门的受力情况进行分析可获得更精确的结果。但有限元法多基于有限元分析软件进行设计计算,操作复杂、耗时长、可复用性差,为解决这一问题,基于人工神经网络预测法进行闸门受力预测分析。人工神经网络是模拟大脑运行机理的机器学习模型,是由多对一的神经元子系统构成的拓扑网络系统[12-13]。基于BP神经网络算法,使用有限元分析数据进行训练,可得到设计参数与受力分析结果的映射关系并应用于优化分析。

2.1 数据前处理

本文采用sigmod函数作为激活函数,参数输入值的值区间为(0,1),故需对输入参数进行归一化处理。而闸门参数输入输出数据数量级差异巨大,因此需对输入数据进行前处理,先统一数量级,统一数量级后获取最大值[x]max,以此为标准进行归一化。前处理过程表示为:

Pi=xi/10Цlogxi/[x]max

(14)

2.2 BP神经网络拓扑结构

输入层:节点数目m=26,包括环境参数(5项),设计参数(21项)。

输出层:节点数目n=5,包括面板正应力,主梁翼缘正应力、主梁切应力,主梁挠度,边梁折算应力。

基于Kolmogorov定理计算隐含层节点数目:

≈11

(15)

2.3 训练数据选取

训练样本数量会对训练结果产生较大影响,训练样本数量太少,训练结果浮动较大,预测结果不准确;如果训练样本数量太大会导致学习时间过长,且权值矩阵计算结果与训练数据过拟合,导致训练结果的归纳能力下降。根据《神经网络专家系统》中观点,网络中节点数与选择样本数量有如下关系;

(16)

根据公式(16)计算,可得受力分析预测模型样本数为29组。

为保证数据选取的普适性,采用工程实例参数与随机生成参数混合的方式生成样本参数数据,随机参数组合是在各个参数的范围内随机生成一组数据。采用以上设计参数数据进行闸门有限元建模计算,获得响应位置应力、变形分析结果作为神经网络训练数据。

2.4 训练结果分析

程序训练时间约为11 min,训练次数5000次,最终均方差0.21899;基于神经网络训练结果结合样本数据进行模拟受力预测分析,分析结果如表2所示。

表2 BP神经网络预测模型模拟计算结果

对表2计算结果分析,可见模拟结果与实际计算值偏差约在2%到6%之间,模拟结果与实际结果近似,验证了使用神经网络对于闸门受力分析和重量预测的可行性。且模拟计算过程速度远远快于有限元法计算速度。

3 改进遗传算法优化闸门结构

遗传算法是一种以达尔文进化学说为基础的仿生学寻优算法,是将随机初始化参数基因集,通过随机选择、交叉、变异进行迭代产生最优解的自适应算法,具有较强的全局搜索能力[14-15]。闸门的门重作为优化目标即目标函数,上文约束条件即惩罚函数,二者共同构成适应度函数。闸门受力条件和水工建筑孔口尺寸为环境变量;闸门各个结构设计变量作为待优化的参数,即遗传算法个体的基因,编码形式采用实数编码。遗传算法过程可分为以下步骤:①基于参数取值范围初始化个体;②根据适应度函数,计算种群中个体适应度;③完成繁殖过程中的遗传操作,选择算子采用轮盘赌算子,交叉采用双亲双子法,交叉概率为0.75,变异基于初始化范围进行,变异概率设置为0.01;④判断种群中是否满足设计条件;⑤完成后输出当前种群中适应度最大个体。具体过程如图1所示。

图1 闸门优化遗传算法繁殖过程

3.1 个体基因初始化

工程中设计变量可以确定一个大致的范围,因此文中选择区间分布法作为初始化基因的方法,即已知基因分布区间或隶属函数后,在区间内随机产生基因组成个体。根据工程经验,个体基因参数限制范围如表3所示。

表3 基因参数限制范围

3.2 适应度函数

遗传算法中的适应度是决定优化结果的主要因素。适应度函数为目标函数和惩罚函数之差。目标函数如式(2)、(3),惩罚函数基于式(4)-(13)约束条件确定:

(17)

规范强制性约束惩罚函数为许用值与设计值之差,Z=1.5。

强度约束中面板正应力、主梁正应力惩罚函数表示为:

p=[[σ]-ANN1,2(Mt,Y1,Y2,…)]2

(18)

主梁切应力惩罚函数表示为:

p=[[τ]-ANN3(Mt,Y1,Y2,…)]2

(19)

主梁挠度惩罚函数表示为:

p=[[η]-ANN4(Mt,Y1,Y2,…)]2

(20)

边梁折算应力惩罚函数表示为:

p=[1.1[σ]-ANN5(Mt,Y1,Y2,…)]2

(21)

其中ANN1-5为根据BP神经网络映射关系计算得到的各受力分析结果。

3.3 选择

本文选择改进轮盘赌选择算子进行选择操作,传统轮盘赌累计概率可以表示为:

Psum=∑P(xi)

(22)

试验发现由于适应度函数个体适应度目标函数基数较大,经过数代繁殖后,惩罚函数逐渐变小,经过十余代繁殖后适应度函数计算结果差异不明显,致使收敛速度极具降低甚至不收敛。故对轮盘赌选择算子进行改进,选择累计概率采用个体与当代适应度最小值之差的总和,可以表示为:

Psum=∑P(xi)-P(xmin)

(23)

改进前后适应度曲线如图2所示,收敛曲线趋向均匀,并在130代左右完成收敛。

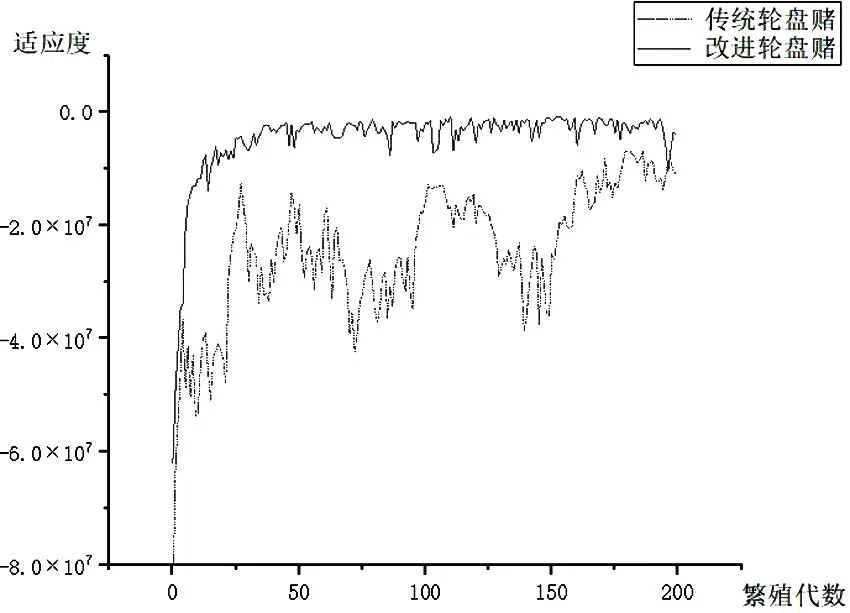
图2 轮盘赌算子改进前后平均适应度曲线

3.4 种群数量

由一定数量的个体构成的集合被称为种群,种群也是个体的一种“环境因素”。种群的数量影响到遗传算法的全局收敛性,数量过少会导致局部最优、早熟等问题;群体数量过大导致计算量激增影响到算法的性能,一般认为,种群数量的常规取值范围为50～200。为保证种群数量选取合理,对选取种群数量进行测试,分析种群在[50,200]区间的平均适应度曲线过程;经试验对比,发现最终收敛适应度在种群数小于100时不断增加,在大于130后趋于平稳,故选取略大于130种群数量150种群数作为算法实际应用种群数。

3.5 遗传算法优化结果分析与对比

本文以兴化小戚闸站工程与大庄闸站工程作为闸门优化算法的应用对比实例,实例采用传统优化法设计。将遗传算法优化结果与应用实例数据进行对比分析。

小戚闸环境变量:

H正=15.347 m,H反=10.047 m,K底=8.3 m,K宽=8.8 m,K高=8.7 m

大庄闸环境变量:

H正=10.56 m,H反=7 m,K底=3 m,K宽=14 m,K高=8.1 m

根据优化结果参数重新计算闸门承载力如表4所示,对比项目数据与优化结果力学分析结果列出的4组计算结果可以看出,各项承载力均可以达到设计要求,且比原设计方法更加贴近极限值,且相比设计方案门重得到了一定程度的优化。根据优化结果可明显看出,项目中承载力的主要控制因素是主梁挠度和边梁折算应力。

表4 项目数据与优化结果力学分析结果

综上所述该算法针对闸门关键结构参数进行优化,优化结果帮助设计人员在闸门设计过程中快速选取结构参数,对闸门设计速度有着显著的提升。

4 总结与展望

本文主要针对平面钢闸门的结构优化设计进行讨论,重点研究了BP神经网络、遗传算法在闸门设计过程中应用的可行性。根据闸门结构受力分析结果,提出基于BP神经网络非线性映射关系的特点,训练并获得闸门主要设计变量与闸门受力分析结果之间的映射关系。解决了设计过程中计算复杂、时间长的问题,但预测精度仍有提高空间。将BP神经网络训练结果与遗传算法相结合,引入适应度函数的构造过程中,解决了适应度函数构造复杂的问题。结构优化设计领域中还存在着如退火算法、蚁群算法、拓扑算法等结构优化算法。使用多种算法结合进行优化的方式是结构优化设计领域研究的主要方向之一;使用多种优化算法组合的优化方式,是否可以提高优化效率,提高优化结果的准确性,也是一个值得研究的问题。本文仅针对平面钢闸门进行研究,面对弧门、底轴翻板门、横拉门等更多门型,该方法是否可行,是否存在改进的空间仍值得讨论。应用设计优化理论,提高结构合理性,充分利用材料性能,降低造价,对于绿色环保等需求更是有着深远的意义。