基于不同抽样方法的核电厂大破口失水事故BEPU 分析

2023-12-31王洋洋孙晓晖石兴伟

科技创新与应用 2023年36期

王洋洋，孙晓晖，石兴伟

（1.电力规划设计总院，北京 100120；2.中国核电工程有限公司，北京 100840；3.生态环境部核与辐射安全中心，北京 100082）

最佳估算加不确定性（BEPU）分析方法同传统的保守性分析方法相比，可获取相对现实的分析结果和安全裕量，能在保证核电厂安全性的前提下，提高核电厂的经济性和运行灵活性。根据国际原子能机构（IAEA）的定义[1]，最佳估算加不确定性分析方法应满足3 个条件：对于选定的验收准则，事故分析中不有意引入悲观性；使用最佳估算程序；对计算结果进行不确定性分析。不确定性分析方法依据不确定性传输主体的不同可分为“输入不确定性传播”方法和“输出不确定性传播”方法[1]。典型的“输入不确定性传播”方法有美国的CSAU 和ASTRUM、德国的GRS、法国的IPSN 和西班牙的ENUSA 等。典型的“输出不确定性传播”方法为意大利的UMAE/CIAU。目前相比“输出不确定性传播”方法，“输入不确定性传播”方法被世界更多国家研究和使用。“输入不确定性传播”方法以热工水力系统程序（最佳估算程序）为不确定性传输媒介，将输入不确定性传播到输出不确定性，其具体流程如图1 所示。基于特定的抽样方法对不确定性重要输入参数进行随机抽样是不确定性评估流程的重要环节，随机抽样参数作为热工水力系统程序的输入，将直接关系到目标响应参数的不确定性量化结果。

图1 基于输入传递的不确定性评估流程

美国核管会（NRC）在1974 年发布的10CFR 50.46 轻水堆核电厂应急堆芯冷却系统（ECCS）验收准则[2]，成为轻水堆保守性失水事故（LOCA）分析的国际通用规范。失水事故验收准则为：包壳峰值温度不能超过限值（1 477 K）以防止包壳脆化；包壳总氧化率不超过氧化前包壳总厚度的17%；燃料包壳与水或蒸汽发生化学反应的产氢量不应超过堆芯所有锆产氢量的1%；堆芯保持可冷却的几何形状；保持对堆芯的长期冷却。NRC 在1988 年对10CFR 50.46 及其附录K 进行了修订，LOCA 验收准则保持不变，允许采用BEPU分析方法进行LOCA 分析，需将不确定性分析结果同验收准则进行比较，确保验收准则规定限制有很高的概率不被超过。尽管许多国家采用TRACE、CATHARE和RELAP5 等最佳估算程序对大破口失水事故（LBLOCA）进行了不确定性分析，但系统地基于不同抽样方法开展响应参数不确定性量化与敏感性分析工作尚无。

本文采用RELAP5 程序建立百万千瓦级压水堆核电厂大破口失水事故模型，并对模型进行稳态调试和瞬态分析；采用Python3.7 基于简单随机抽样（SRS）和拉丁超立方抽样（LHS）对重要不确定性输入参数进行随机抽样产生模型输入矩阵，通过模型对输入矩阵实施计算获取关键安全参数；采用Wilks 非参数统计方法对关键安全参数进行不确定性量化以获取单侧统计容忍上限，采用Spearman 秩相关系数法对关键安全参数进行敏感性分析以识别主要影响的输入参数。并评估2 种抽样方法在不确定性量化和敏感性分析中的计算结果的差异。

1 模型建立

1.1 程序介绍

RELAP5/MOD3.4 程序基于非均匀、非平衡、两流体动力学模型，采用快速半隐式数值技术求解，能够模拟反应堆在几乎各种运行瞬态或假想事故下的行为，广泛应用于事故分析、规程制定、审评计算和事故缓解措施评价等各个方面。是目前国际通用的轻水堆热工水力瞬态分析程序，可用于反应堆破口类事故分析。

1.2 模型建立

某百万千瓦级压水堆核电厂采用我国具有完整自主知识产权的第三代压水堆核电技术。核电厂主系统具有3 个环路，每个环路有1 台主泵和1 台蒸汽发生器，系统共用1 台稳压器。反应堆热功率为3 180 MW，冷却剂平均温度为310℃，系统正常运行压力为15.5MPa。

采用RELAP5/MOD3.4 程序针对百万千瓦级压水堆核电厂的设计特点，对大破口失水事故建立最佳估算分析模型，系统节点划分如图2 所示。建模对象主要包括反应堆压力容器、稳压器、蒸汽发生器、主泵、主蒸汽系统、安注系统、主给水系统、辅给水系统、主管道和破口等。其中，压力容器针对入口、下降环腔、下封头、下腔室、堆芯通道、堆芯旁通通道、上腔室和上封头等进行了模拟。安全壳采用时间相关控制体进行模拟，大破口失水事故的发生通过触发阀打开进行模拟。

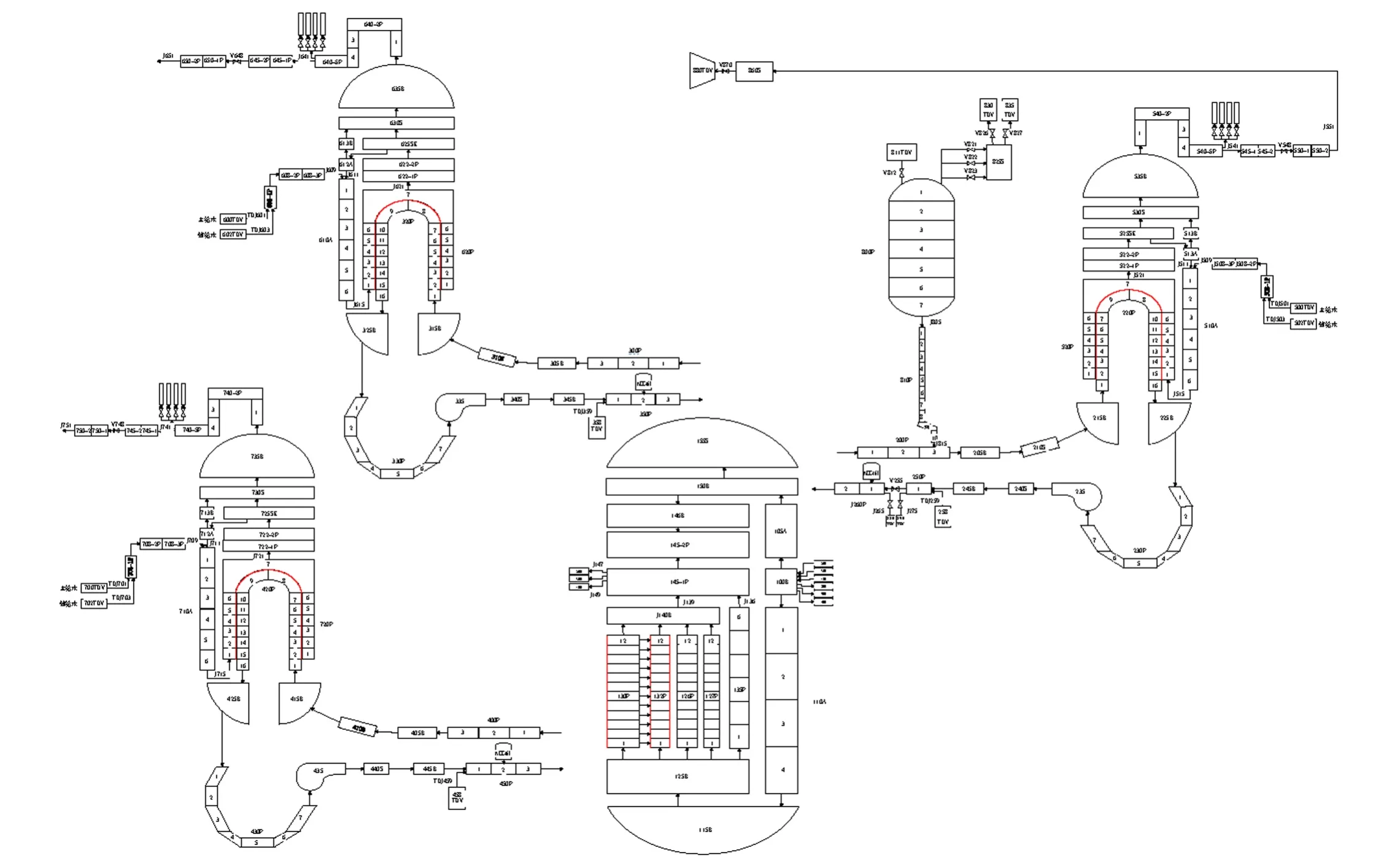
图2 RELAP5 系统节点

1.3 稳态调试

在进行大破口失水事故瞬态计算之前，需要对建立的模型进行稳态调试，以确保各主要参数同电厂名义值一致。表1 为模型的稳态计算值和电厂名义值的相对偏差，从模型稳态计算结果可见，主要参数模型稳态计算值和名义值符合较好。

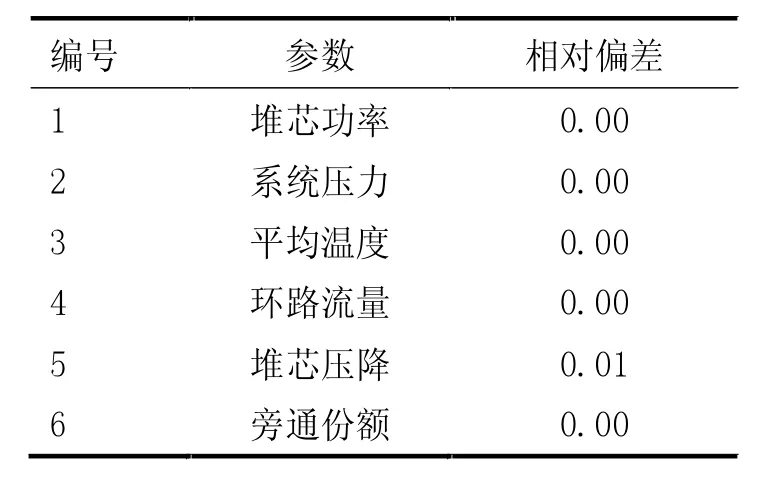
表1 模型稳态计算值相对偏差%

1.4 瞬态计算

模型在稳态运行1 000 s 后发生冷管段双端剪切断裂大破口失水事故，事故瞬态计算时间为300 s，大破口失水事故事件序列见表2。图3—5 分别为大破口失水事故下归一化堆芯功率、稳压器压力、破口总流量的模型计算曲线和参考曲线。从瞬态计算结果可见，计算曲线与参考曲线大小趋势基本一致。

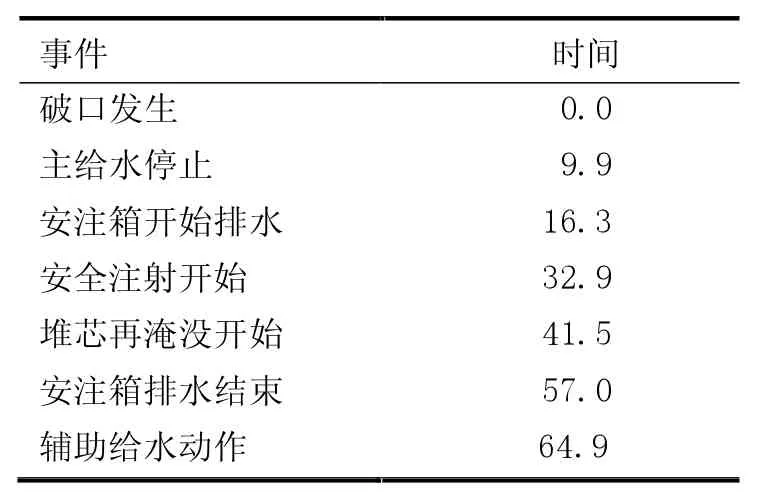
表2 大破口失水事故事件序列s

图3 堆芯功率

图4 稳压器压力

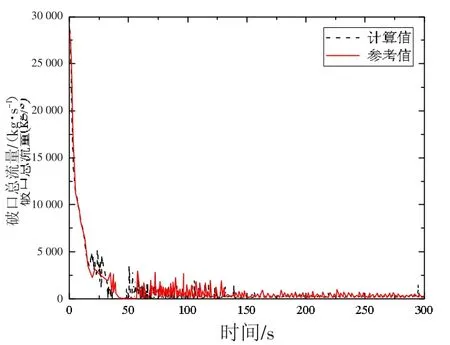
图5 破口流量

2 理论方法

2.1 简单随机抽样

2.1.1 均匀分布参数的简单随机抽样

对于均匀分布参数，简单随机抽样实现步骤如下。

1）通过公式（1）采用Python3.7 程序中的random 模块调用random（）方法生成0 到1 之间的随机浮点数u。

式中：random 为Python3.7 程序中的模块，random（）为模块中的方法。

2）通过公式（2）将随机浮点数u映射为参数分布范围内的随机数。

式中：a为均匀分布参数的下限，b为均匀分布参数的上限。

2.1.2 正态分布参数的简单随机抽样

对于正态分布参数，简单随机抽样实现步骤如下。

1）通过公式（1）采用Python3.7 程序中的random 模块调用random（）方法生成0 到1 之间的随机浮点数u；

2）将u视为标准正态分布的分布函数值，采用公式（3）借助标准正态分布反函数映射到上1-u分位点z；

式中：z为标准正态分布的上1-u分位点，ϕ-1为标准正态分布的反函数。

3）采用线性变换公式（4）将z映射为正态分布抽样散点。

式中：σ 为正态分布的标准差，μ 为正态分布的期望值。

2.2 拉丁超立方抽样

2.2.1 均匀分布参数的拉丁超立方抽样

对于均匀分布参数，拉丁超立方抽样[3]实现步骤如下。

1）将均匀分布参数的取值范围等概率分割为满足公式（5）的N个子区间；

式中：X为随机变量，Ii为等概率区间坐标值。

2）采用公式（6）将0 到1 之间的随机浮点数u映射为归一化区间的各子区间的随机数；

3）通过公式（7）将随机数zi映射为参数分布范围内的随机数；

2.2.2 正态分布参数的拉丁超立方抽样[3]

对于正态分布参数，拉丁超立方抽样实现步骤如下。

1）依据公式（8）将正态分布参数区间进行等概率划分

2）通过公式（9）将0 到1 之间的随机浮点数u映射为归一化区间的各子区间的随机数；

3）将νi视为标准正态分布的分布函数值，采用公式（10）借助标准正态分布反函数映射到上1-νi分位点wi；

4）采用线性变换公式（11）将wi映射为正态分布抽样散点。

2.3 Wilks 非参数统计

Wilks 非参数统计方法[4]广泛应用于BEPU 统计分析中。基本思想是通过Wilks 公式根据选定的置信水平和概率水平获取最小的计算次数，通过对响应参数的有序统计理论来获取统计容忍区间。

对于概率密度分布函数g（y），确定一统计容忍区间（L，U），此区间对y的覆盖率至少为γ 的概率为β，通过式（12）表示为

式中：β 为置信水平，γ 为概率水平，L为容忍下限，U为容忍上限，P为概率。

依据有序统计理论和多项式分布定律可推导出单侧统计容忍区间Wilks 公式为

式中：N为计算次数。

Wilks 非参数统计方法具有黑箱统计模型的特点，由公式（13）可知：计算次数仅与置信水平和概率水平有关，与输入变量的数量及其概率密度分布无关。Guba[5]在2003 年将单侧统计容忍区间Wilks 公式推广到下式

式中：p为输出变量数量。

依据Wilks 非参数统计方法，采取95%置信水平和95%概率水平（简记为95/95），若只有一个输出变量，确定95/95 单侧统计容忍上限至少需进行59 次运算，取59 次运算最大值；若计算次数为93 次，取次大值作为95/95 单侧统计容忍上限；若计算次数为124次，取第三大值作为95/95 单侧统计容忍上限。

3 不确定性量化与敏感性分析

3.1 输入参数抽样

主要依据大破口失水事故PIRT 表[6]，综合考虑大破口失水事故过程中燃料棒、反应堆堆芯、换料水箱和安注箱等重要部件重要现象，识别大破口失水事故下对关键安全参数PCT 有重要影响的模型参数、电厂参数（电厂初始条件和电厂边界条件），并结合相关资料等多种方式综合确定不确定性输入参数。选用的不确定性输入参数见表3。对各种不确定性输入参数的范围和概率密度分布，结合核电站设计文件、已有的相关文献资料及工程经验判断加以判定。在信息不足的情况下，不确定性输入参数通常假设为均匀分布。

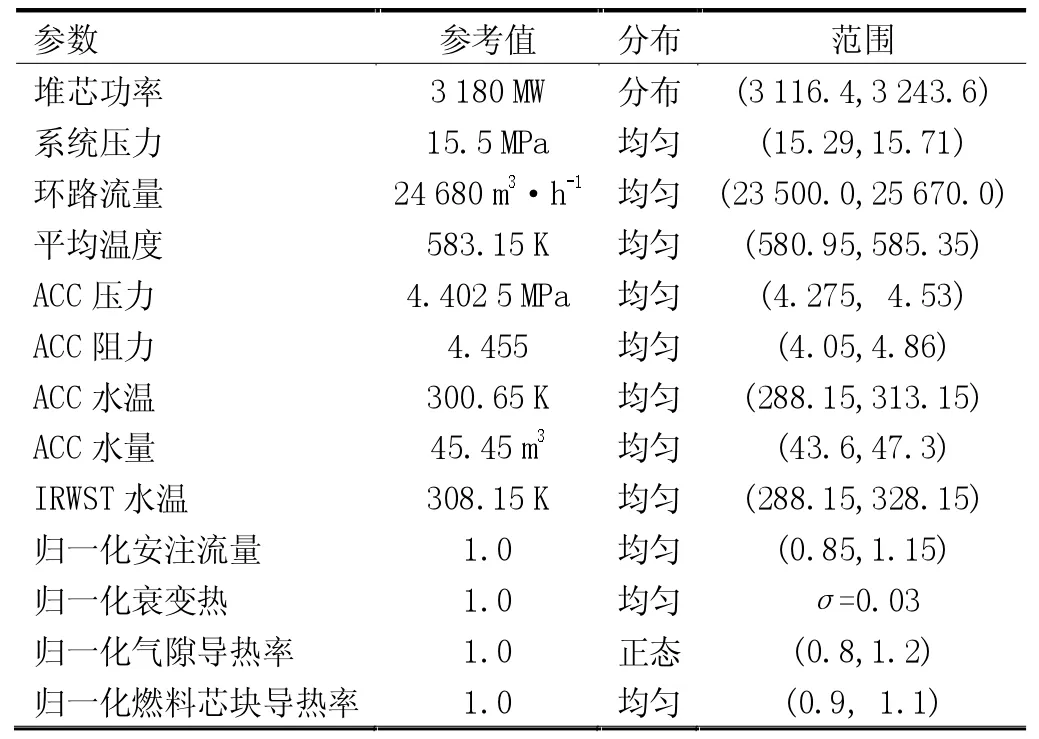
表3 不确定性输入参数

采用Python3.7 程序调用Mersenne Twister 随机数产生器。对不确定性输入参数分别进行124 次简单随机抽样和拉丁超立方抽样。

可见抽样散点反映了输入参数的分布特征，对于均匀分布的输入参数，散点在取值范围内分布均匀。对于正态分布参数，散点分布呈现出中间聚集效应。拉丁超立方抽样比简单随机抽样散点分布更加均匀。以堆芯功率散点分布为例，简单随机抽样相邻散点距离的标准差为0.517 7，而拉丁超立方抽样相邻散点距离的标准差仅为0.252 6。

3.2 不确定性量化

将简单随机抽样和拉丁超立方抽样结果组合作为RELAP5/MOD3.4 程序输入并执行计算，得到基于2 种抽样的124 组热点处燃料包壳温度瞬态曲线。通过AptPlot 程序提取热点处包壳峰值温度数据。相应的包壳峰值温度散点分布如图6 和图7 所示。

图6 基于SRS 的124 组PCT 散点

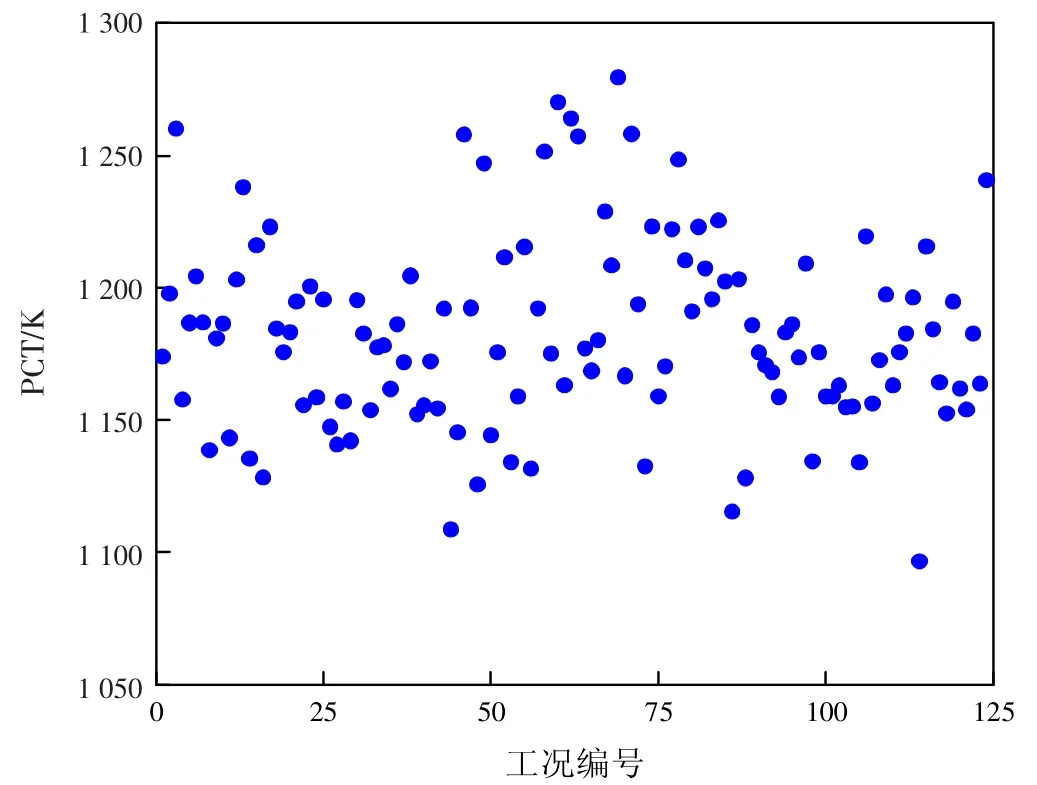
图7 基于LHS 的124 组PCT 散点图

将124 组包壳峰值温度由大到小进行排序，根据Wilks 非参数统计理论可知，排序第3 位的值即为包壳峰值温度, 在95%置信水平上具有95%概率水平的单侧统计容忍上限。基于简单随机抽样计算得到包壳峰值温度单侧统计容忍上限95/95PCT 为1 264.057 K，基于拉丁超立方抽样计算得到包壳峰值温度单侧统计容忍上限95/95PCT 为1 267.617 K。基于2 种抽样方法得到的包壳峰值温度，单侧统计容忍上限均低于验收准则规定的限值1 477 K。基于2 种抽样方法得到的包壳峰值温度单侧统计容忍上限较为接近，仅相差3.56K。

3.3 敏感性分析

Spearman 秩相关系数法作为全局敏感性分析方法[7]，可检验多个输入参数对响应参数的全局影响。采用Spearman 秩相关系数作为输入参数对包壳峰值温度敏感性的度量。Spearman 秩相关系数的绝对值大小表示敏感性强弱，其计算公式为

式中：RXi为Xi在X中的大小排序，RYi为Yi在Y中的大小排序。

基于简单随机抽样和拉丁超立方抽样的不确定性输入参数与包壳峰值温度间的Spearman 秩相关系数如图8 和图9 所示。

图8 基于SRS 输入参数的Spearman 秩相关系数

图9 基于LHS 输入参数的Spearman 秩相关系数

基于简单随机抽样的敏感性分析结果表明包壳峰值温度对衰变热、换料水箱水温、安注箱水温和气隙导热率较为敏感；基于拉丁超立方抽样的敏感性分析结果表明，包壳峰值温度对衰变热、换料水箱水温、安注箱水温和气隙导热率较为敏感。因此采用Spearman 秩相关系数法基于2 种不同的抽样方法识别出的包壳峰值温度四大主要影响参数相一致。