基于模式匹配法的矩形波导感性膜片不连续性分析

邓 迪

(贵州省机械电子产品质量检验检测院,贵州 贵阳 550001)

0 引言

利用MEMS技术加工制造的THz矩形波导滤波器,因其优越的性能在微波毫米波电路领域得到了越来越多的关注[1-5]。传统的等效电路分析法仅考虑波导以主模传输,忽略了金属膜片实际厚度,且由于THz矩形波导滤波器结构尺寸微小,在实际加工制造时极易引起表面粗糙和结构不连续,所以得到的理论分析结果与实际测试结果往往存在较大误差,不能满足精度要求[6]。

模式匹配法是一种基于场理论的高精度数值分析方法[7],因其考虑到了矩形波导内由于不连续性引起的高次模及其相互影响,进而考虑到了凋落的TE、TM模对于电磁场的贡献,最终能够对矩形波导感性膜片不连续结构进行精确分析。

本文利用模式匹配法首先对矩形波导感性膜片不连续性进行分析,然后对THz矩形波导滤波器进行整体仿真,并与高频电磁场仿真软件HFSS的仿真结果进行比较,两者吻合良好。

1 理论分析

利用模式匹配法分析时所需的电磁场分量由激励波导的主模和波导内不连续性所激发的高次模场分量共同决定[8]。图1为具有H面双边不连续性的矩形波导不连续性结构,假设由主模TE10模激励,入射波场分量除了(Ey,Hx,Hz)外没有其他场分量,所以不连续性处的场分量可以只由TEm0模来描述。

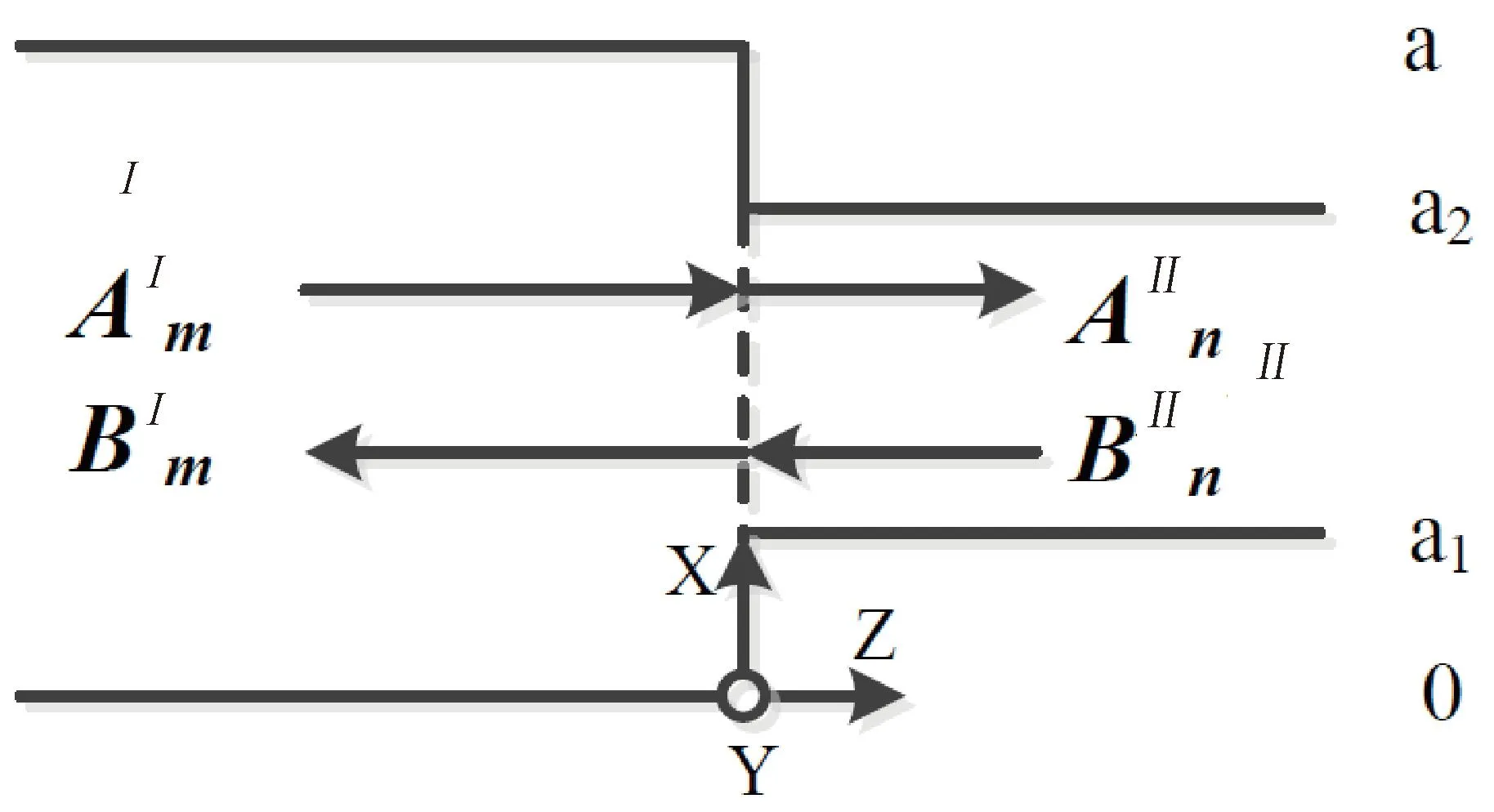
图1 矩形波导H面双边不连续结构

Ⅰ区和Ⅱ区在不连续平面的切向场分量为:

(1a)

(1b)

其中:

(2)

(3)

(4)

(5)

(6)

(7)

Ⅰ区和Ⅱ区不连续平面交界(Z=0)处所满足匹配场分量的边界条件为:

(8a)

(8b)

(8c)

将式(1)代入式(8),可以得到:

(9a)

(9b)

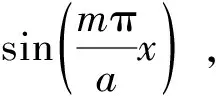
(10a)

(10b)

其中:

(11)

将(10a)(10b)表示为入射波和散射波的形式:

(12)

其中:

S11=[LELH+I]-1[LELH-I]

S12=2[LELH+I]-1LE

S21=LH{I-[LELH+I]-1[LELH-I]}=LH{I-S11}

S22=I-2LH[LELH+I]-1LE=I-LHS12

(13)

因为S11、S12、S21、S22是矩阵而不是某一个具体的数值,所以式(12)中的矩阵称为广义散射矩阵。

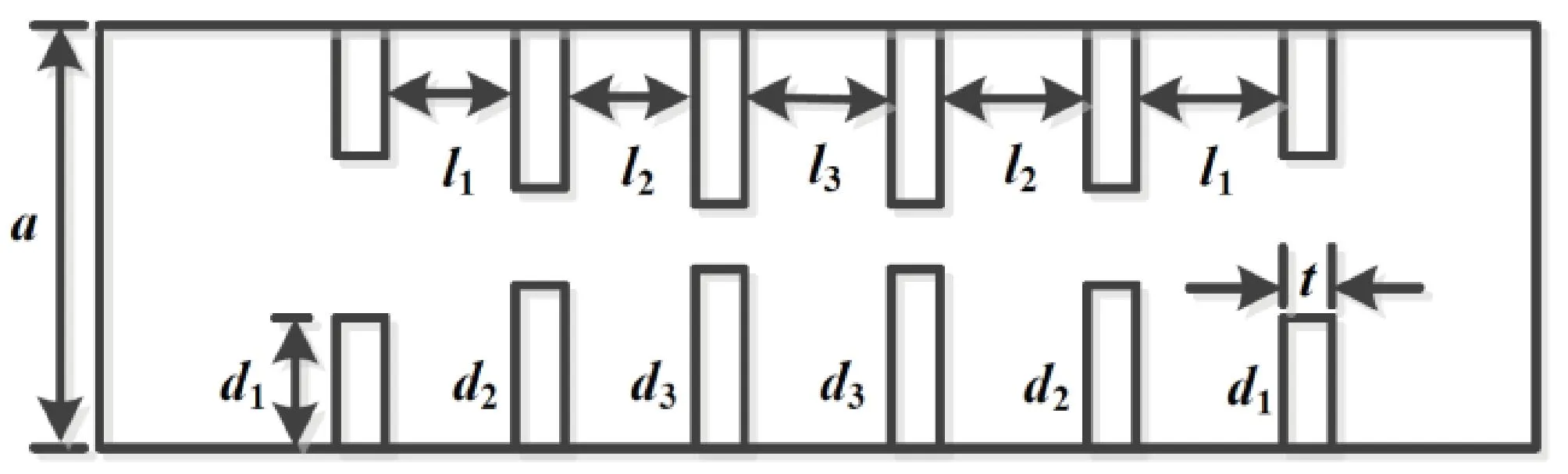
图2 矩形波导感性膜片滤波器结构

(14)

其中,D为对角矩阵:

(15)

根据上面的分析结果,将Z=0,Z=t以及感性膜片散射矩阵级联可以得到感性膜片基本单元的散射矩阵,基本单元的散射矩阵为:

Sk11=S11+S12DW1S22DS21

Sk12=S12DW1S21

Sk21=Sk12

Sk22=Sk11

(16)

其中:

W1=I/(I-S22DS22D)

(17)

其中,I为单位矩阵,最后将所有感性膜片基本单元按照式(18)级联就可以得到整个感性膜片矩形波导滤波器的散射矩阵。两个散射矩阵级联的公式为:

Sc11=Sa11+Sa12Sb11W2Sa12

Sc12=Sa12(I+Sb11W2Sa22)Sb12

Sc21=Sb21W2Sa21

Sc22=Sb22+Sb21W2Sa22Sb12

(18)

其中:

W2=I/(I-Sa22Sb11)

(19)

2 仿真结果

在利用上述模式匹配法对矩形波导感性膜片进行不连续性分析的基础上,本文对Zhao等[9]中的感性膜片矩形波导滤波器编写了MATLAB仿真程序。滤波器为5腔滤波器,共有6对膜片,尺寸参数如表1所示。中心频率f0为140 GHz,带宽Δf为14.5 GHz,带内插入损耗小于1 dB。

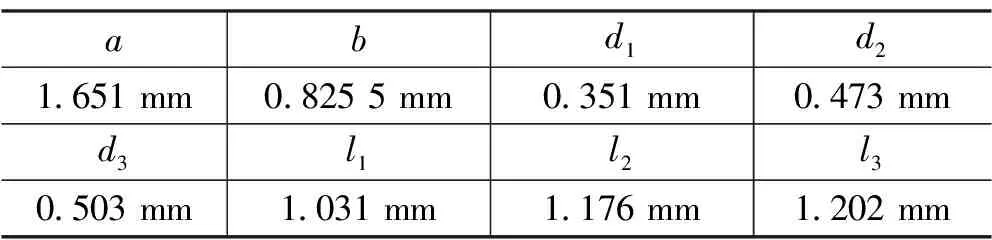
表1 滤波器设计尺寸

图3是模式数N分别取5、15和25时滤波器的S参数曲线,可以看出N=15时已经得到很好的收敛。图4是相同尺寸矩形波导滤波器在三维电磁仿真软件HFSS中仿真结果与模式匹配法理论分析结果的对比图,可以看出两者吻合良好。

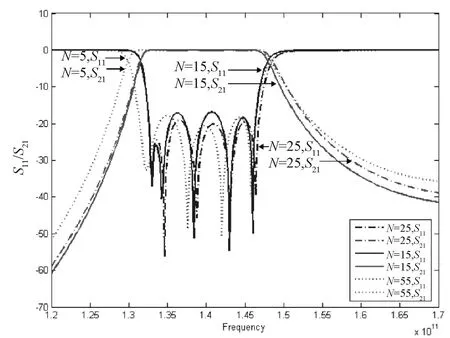
图3 不同模式数下滤波器的S参数曲线

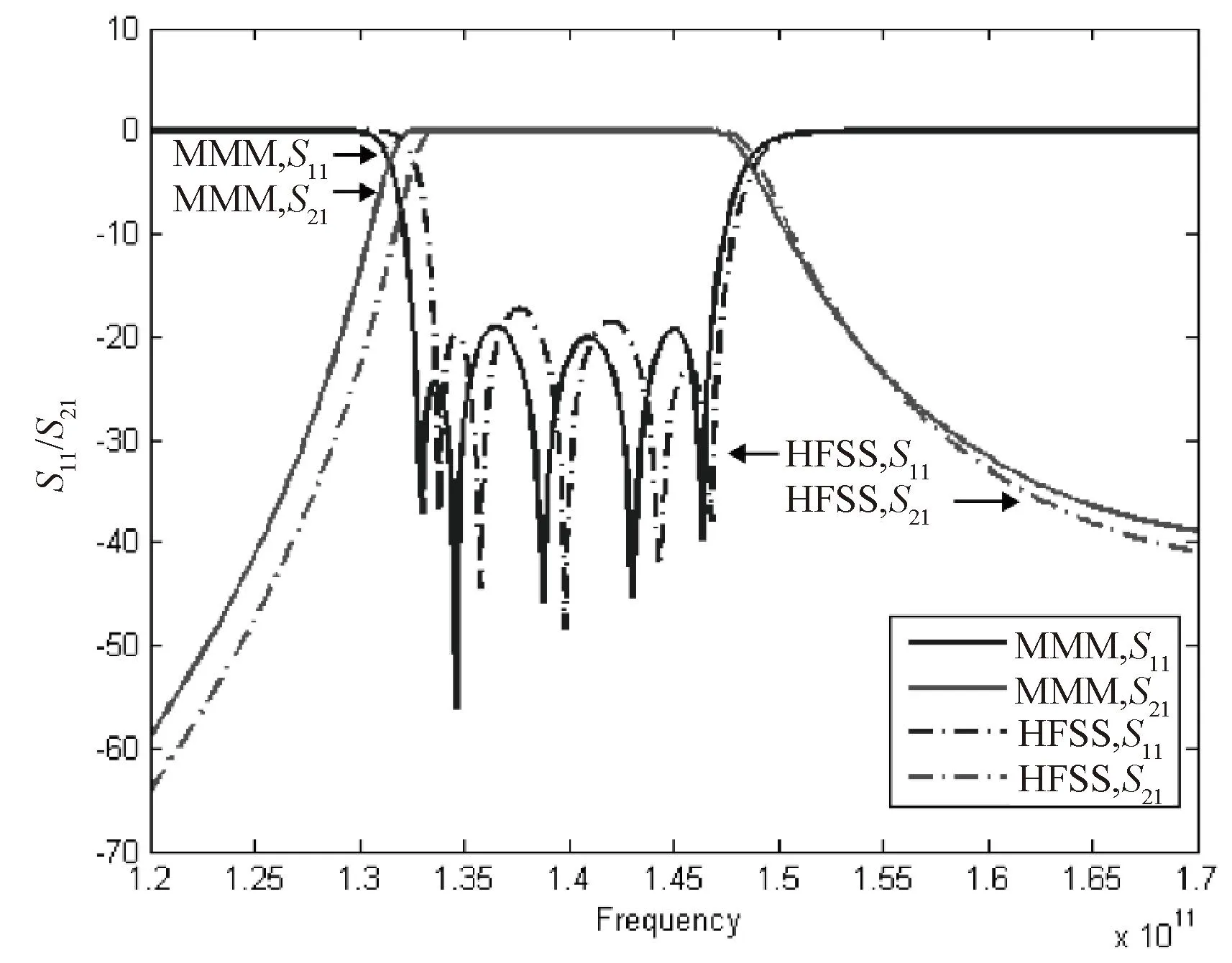
图4 模式匹配法理论分析结果与HFSS仿真结果

3 结语

本文采用模式匹配法对矩形波导感性膜片不连续性进行了分析,并对THz矩形波导感性膜片滤波器S参数特性进行了仿真,由于该方法考虑了高次模及感性膜片厚度的影响,所以数值计算结果与HFSS仿真结果吻合良好。