从操作到思考，从个数到思路

[一、回忆旧知，唤醒经验]

1.回忆长方形和正方形的面积。

师：今天我们来研究平面图形的面积，谁来说说我们已经学过哪些平面图形的面积？

生：长方形和正方形的面积。

师：它们的面积是怎样计算的？

生：长方形的面积=长×宽，正方形的面积=边长×边长。

师：回顾一下，我们在研究长方形和正方形的面积时是怎么做的？

生：用单位面积的小正方形拼摆，看看一行有几个，一共有几行，得出长方形和正方形的面积计算公式。

2.猜想平行四边形的面积。

师：（出示图形，图略）你觉得我们可以怎样研究这个平行四边形的面积呢？

生：继续用单位面积的小正方形拼摆。

生：可以用单位小菱形铺满整个平行四边形，数一数有多少个小菱形。

生：用形状完全一样的小菱形作为面积单位，如果知道一个小菱形的面积，拼摆后就可以得出平行四边形的面积。

师：这位同学会迁移旧知，尝试用菱形作为面积单位拼摆，整个小菱形看起来像“打了折扣”的小正方形面积，给我们很好的启发。还有不同的思路吗？

生：用底和高相乘得出平行四边形的面积。

师：还有不同的想法吗？

生：用两条邻边相乘得出平行四边形的面积。

师：这条边是平行四边形的底，这条边和底边相邻，我们就叫它邻边。老师把你的猜想记下来，那就是底×邻边。

思考：回顾旧知，利用已有知识迁移引出平行四边形面积的探究方法，借助已有学具和基本经验促进对平行四边形面积的理解。

[二、猜想探究，经历过程 ]

1.小组合作，猜想验证。

师：到底哪一种猜想是正确的呢？下面我们来验证一下，请拿出学具，利用学具验证你们的猜想。根据你的计算方法，测量出相关数据，在纸上写出算式和结果。

生：我用的是数格子的方法，先数整格，然后把不够整格的拼起来，凑成整格，这样最后数得28个。

师：这种方法面积有变化吗？

生：面积没有变化，数完后还是28个面积单位，也就是28cm2。

师：还有不同的数的方法吗？

生：我只是数了一行，我把最上面一行左边的半个小格移动到右边，凑成一个整格，一共是7个小方格，因为有4行，都重复了，所以我觉得数出一行，再乘4，就得出面积。

师：根据刚才数的过程，你觉得应该用哪种猜想来计算？

生：数了一行，再数有几行，一行是平行四边形的底，有几行是平行四边形的高，得出平行四边形面积可以用底乘高来表示。

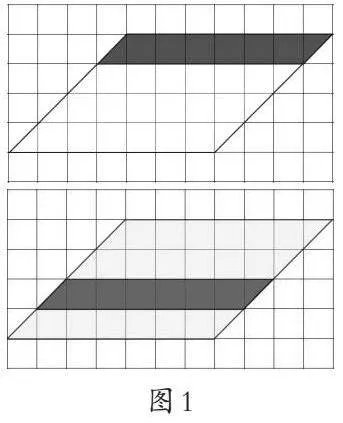
师：经过同学们的验证，我们利用数格子的方法发现，用一行的个数×行数的确能求出平行四边形的面积。（如图1，单位：cm）

思考：在数格子的过程中探寻平行四边形的面积。“通过左右拼移的方法”来解决问题，为后面进一步使用“剪拼割补法”探究新知做了铺垫。这种数是一个从低阶思维到高阶思维的过程，从简易的机械操作到动脑思考，将逐行数变成只数一行，运用乘法进行计算，在实证探究过程中经历了从猜想到验证，从数到计算的动态生成过程，对于培养学生理性精神起着重要的作用。

2.转化图形，推导公式。

师：刚才几个小组的同学都用数的办法，我还发现有的小组用的是剪拼的方法，你们是怎么想到这种方法的呢？

生：一个一个数还是有点麻烦，通过观察，发现如果沿着高剪下来整体平移到右边，就能很容易数出面积。

师：这是一种不错的方法，接下来我们以小组为单位继续深入研究，仔细观察、思考转化后的图形与原来平行四边形有什么联系，能不能根据转化后的图形推导平行四边形的面积计算公式？

生：沿着平行四边形的高剪下左边的直角三角形，然后把这个三角形向右平移，两条斜边重合后拼成一个长方形，长方形的面积是长乘宽，也就是平行四边形的面积。

师：同学们注意到刚才他是沿着什么来剪的吗？

生：沿着平行四边形的高。

师：为什么要沿着高剪呢？

生：因为沿着高剪能保证拼成的新图形是长方形。

师：拼剪后的图形与原来的图形相比，什么变了？什么没变？

生：形状变了，面积大小没有变。

……

思考：我们在此所关注的已不再是如何进行实际度量，而主要是怎么算，如何能够发现转化的方法。这一发展意味着由动手测量转向了动脑思考。

师：刚才同学们都是沿着这条高来剪的，还有其他方法吗？

生：沿着平行四边形的一条高将它剪为两个直角梯形，把其中一个梯形向另一边平移，平移到斜边重合的位置。

师：只要沿着高剪，任意一个平行四边形都可以沿高分成两部分，然后拼成一个长方形。所以平行四边形的面积都可以转化为长方形的面积来求，从而得到：平行四边形的面积=底×高。像这样将平行四边形变成长方形来研究问题的方法叫“转化”。

3.释疑解惑，刨根问底。

师：同学们很好地解决了求平行四边形面积的问题，还记得有同学猜想用底乘邻边的方法来计算平行四边形的面积，能说说你当时是怎样想的吗？

生：长方形可以拉成平行四边形。长方形的面积是相邻的两边相乘，即长×宽，所以我觉得平行四边形面积可以用底×邻边来求。

师：请同学们以小组为单位，操作学具，看看你们有什么发现。

（学生通过操作、展示，发现可以将右边多的部分补到左边，拼成的长方形的面积比原来长方形的面积小）

师：在超级画板演示下，仔细观察平行四边形框架逐步变形的过程，什么在变？什么没有变？

生：平行四边形的底和邻边的长短没有变化，所以周长是不变的。

师：还有什么发现？

生：两邻边夹角变小，会引起高变小，面积也随之变小了。

师：通过刚才的演示，你有什么发现？

生：平行四边形的面积应为底×高，而不是底×邻边，因为两条邻边的夹角会发生变化。

师：如果用“底×斜边”这种猜想算面积的话，那平行四边形的面积会变吗？

生：不会变。

师：想象一下，如果继续这样拉下去，实际面积又会有什么变化？为什么？

生：因为平行四边形的面积等于底乘高，而不是底乘斜边，所以它的面积会一直变小，最后会变成0。

思考：在动态的超级画板演示中，引导学生发现平行四边形边、角的变与不变，从变化中找到引起平行四边形的面积变化的根源。在这个“压扁”的过程中，底没有变化，高在不断变小，导致面积也随之变小，学生由此理解和掌握高的变化会引起面积的变化。

（作者单位：山东烟台高新技术产业开发区益文小学）