解构测量工具，实现深度理解

度量的本质是用计量单位与被测物体比较，从而获取数值来表示物体的属性。角的度量的本质是通过1°的角的累加获得角的两条边张开大小的程度。“赋角以数”实现了数形结合，并促进学生的空间想象由一维向二维发展。角作为二维图形有其独特的特点，不同于长方形面积的测量可以转化为先利用直尺测量再算长和宽之积，角的测量有自身的工具——量角器。量角器的构造比直尺复杂。如何实现对量角器的深刻认识呢？我们进行了多次课堂实践，形成了以下路径（如图1）。具体教学流程如下。

一、建构关联

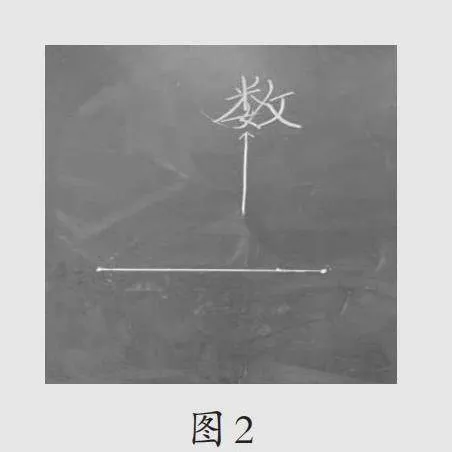
教师在黑板上呈现图2。

师：你们明白老师的意思吗？

生：想用数表示这条线段的长度。

师：用哪个数表示这条线段的长度呢？随意找一个数吗？

生：用35厘米，我估计有这么长。

师：精确吗？

生：用直尺测量一下。

教师随即让该生上来测量，该生发现教师提供的是一把断尺。该生将线段的一端对准断尺上的8cm刻度线，另一端到48cm刻度线，再计算48-8=40，得出这条线段长40cm。

师：把掌声送给他。这个过程叫“赋线以数”。

师：（把线段的一个端点擦掉）这时它还可以用40cm表示吗？

生：不能，因为它变成了射线，射线是无限长的。

师：（边演示边解说）这条射线绕着端点逆时针旋转，旋转到一个位置后悄悄地停了下来，这样就形成了另一种图形（如图3），这个图形是什么？

生：这是锐角。

师：你们能用数表示这个锐角的大小吗？

生：可以用直尺测量。

师：请试一试。

生：（测量一条边的长度）我测量这条边，是27cm。

生：（测量另一条边的长度）我测量这条边，是25cm。

师：角的两条边是射线，射线是无限长的，所以无法测量其长度。

生：我在角的两条边上分别取10cm长，再将两个点连起来测量，是29厘米。

师：这是一种方法，和大家以后要学的弧度有相通之处。谁还有其他办法？

生：我用三角板上的直角进行估测（用三角板上的直角进行比画），发现大约是45°。

师：这个学生用的是估测法。下面我们一起来看看城关小学和西城小学的同学给出的方法（如图4）。

师：为什么同一个角，却有不同的结果呢？一个是3个小角，另一个是6个小角。

生：他们使用的小角大小不一样。

师：也就是说，他们的测量标准不一样。

二、探索方法

师：那么有没有统一的标准呢？古巴比伦人将圆平均分成360份，每份对应的就是1°的角（呈现1°的角形成的过程），同学们，现在请用一个词语形容一下对1°的角的感觉！

生：超级小。

生：跟指甲的厚度差不多。

生：非常细，简直像一条线。

生：微不足道。

师：（呈现10°的角）现在请说一说对10°的角的感觉。

生：尖尖的，是个锐角，有点儿大。

生：由10个1°的角组成。

师：（出示20°的角）请仔细观察并估计一下大约是多少度。

生：20°。

师：请验证！

学生利用10°的角进行对比，发现的确是20°。

师：（呈现30°的角）请仔细观察并估计一下大约是多少度。

生：30°。

师：请验证，并介绍你的方法！

生：我把10°的角与20°的角合并，发现的确是30°。

师：好办法（随机在黑板上接着粘贴2个30°的角，如图5），猜猜这些角组成了多少度的角。

生：10+20+30+30=90（度）。

师：这是什么角？

生：直角。

师：（随机又粘贴一个90°的角，图略）此时变成了多少度？是什么角？

生：180°，平角。

师：如果再加一个半圆呢？

生：360°，周角。

师：感觉真好！

师：现在找到测量角的工具了吗？

生：找到了。

师：请测量此角（如图6）的大小。

生1：（利用刚才的10°、20°、30°的角进行测量，嘀咕“小角不够用”）50°多一点儿。

生2：可以把10°的角分小点儿再进行测量，但是有点儿麻烦。

师：是呀，确实麻烦！于是人们开始琢磨创造更加简单的工具，这时“量角器的爸爸”（如图7）出现了，请仔细观察上面的数学信息！

生：上面有清晰的刻度，而且从0°到180°逆时针排列。

教师引导学生探索用“量角器的爸爸”量角的方法，学生体会到比刚才的用小角量方便。接着，教师出示一个开口向左的角，学生在用“量角器的爸爸”测量的时候，感觉到不方便，由此逐步探索出“量角器的妈妈”（如图8）。最后，学生对比，说出它们的不同。

师：这样，我们测量角度的时候，带着“量角器的爸爸”“量角器的妈妈”就可以了。

生：带两个，有点儿麻烦。

师：于是聪明的人们将它们合二为一，制造出了你们手中的量角器（利用课件呈现量角器的结构图，并请全体学生起立将手中的量角器与结构图进行对照）。内圈遗传了谁的相貌特征？外圈遗传了谁的相貌特征？

生：内圈遗传了“爸爸”，外圈遗传了“妈妈”。

师：用这个量角器测量角，你会有什么感觉？

生：不用换来换去。

生：更简单、实用。

三、全课小结，埋下伏笔

师：你们的感觉真好！你们能给这节课起个名字吗？

生：认识量角器。

生：测量角的大小。

生：量角器的使用。

师：看来，你们对角的测量有不同的感觉。同学们都会使用量角器了吗？咱们下节课拭目以待。

本节课依托两个开口方向相反的锐角作为研究素材，把量角器的构造及人们对工具的开发有机结合起来，解剖量角器的结构。在这节课上，断尺的使用打通了“赋线以数”“赋角以数”之间的本质关联（测量就是赋形以数）；由线段的测量过渡到角的测量，实现了一维到二维空间的转换；学生采用多种方法尝试测量角，都是基于原有的思维经验和操作经验，渗透了度量的本质属性——正则性、运动不变性、有限可加性；“量角器的爸爸”“量角器的妈妈”与量角器上的内圈刻度、外圈刻度及各自功能有效对接，充满着智慧的火花。

【本文系安徽省六安市教育信息化课题“智慧课堂环境下小学数学深度学习案例研究”（立项号：LA202122）的研究成果】

（作者单位：安徽霍山县衡山镇东城中心学校）