“问题”与“探究”的最美相遇

深度学习是促成核心素养发展的关键路径，如何让“问题”与“探究”的最美相遇焕发深度学习的活力呢？笔者以人教版教材五年级上册“平行四边形的面积”一课的教学为例进行了尝试和探索。

一、问题点醒——唤醒旧知，激发内需

师：黑板上有一个长方形的框架。我们已经掌握了长方形哪些方面的知识？

（学生回答长方形的周长和面积，教师板书：S长方形=ab）

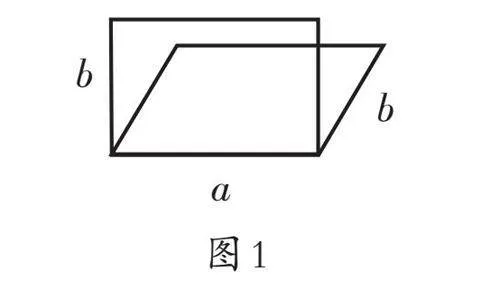
师：现在老师给大家表演个魔术，请看！变！这样一推，长方形的框架变成了一个平行四边形（原来有两个相同长方形框架重叠在一起），变成平行四边形后，（如图1）原来a这条边还在吗？它的长度变了吗？b在哪？它的长度变了吗？

（学生指出a和b的长度都没变）

师：这个平行四边形的面积是指哪一部分的大小呢？

（学生上来比画，教师用阴影表示出平行四边形的面积）

师：你会求这个平行四边形的面积吗？

（学生争相举手，有部分学生沉思或摇头）

师：在现实生活中经常需要求出平行四边形的面积。这节课我们来研究平行四边形的面积。

【思考】通过魔术引入，不仅让学生唤醒了旧知，引发了新的问题，还在学生的脑海中沟通了长方形与平行四边形之间的联系。

二、探索点燃——暴露思维，启发猜想

师：请大家先猜一猜，这个平行四边形的面积应该怎样求呢？可以独立思考，也可以同伴之间讨论一下。（学生思考讨论后）有想法的同学请举手。

生：S=ab，a和b的长度没变，我认为平行四边形的面积和长方形的面积一样，还是等于a乘b。

师：其他人还有想法吗？

生：平行四边形的面积等于底乘高。

师：这位同学的猜想真有意思，哪一条是底？哪一条是高？请你指一指，能否也用一个字母表示这条高呢？

生：可以用h表示。

师：我们的问题是如何求平行四边形的面积。（板书：问题）有人说面积等于a乘b，有人说不是a乘b，这就是猜想。（板书：猜想）猜想是否正确呢？就要进行验证，（板书：验证）验证后才能得到结论。（板书：结论）接下来我们该进入什么环节？

生：验证。

【思考】深度学习的基础在于能否直面儿童立场的问题。根据课前对学生的调查，发现学生虽然在日常生活中常常接触到平行四边形，但是对平行四边形面积计算公式的理解还处于模糊阶段，由于受长方形面积计算公式负迁移影响，有58.5%的学生认为平行四边形的面积等于“邻边相乘”，有20%的学生只是从书中了解到计算公式，但不太理解其中的道理。通过这个有趣的情境引入，学生根据已有的经验和思考大胆提出猜想，能暴露学生真正的想法；同时渗透了解决问题的一般路径——“问题—猜想—验证—结论”，让学生积累解决问题的经验。

三、“问探”点睛——思之所向，追本溯源

1.创新学具，“解”负迁移。

师：好，我们就先验证第一种猜想，S=ab。

出示活动要求：

（1）可以独立研究或者小组讨论。

（2）选择喜欢的材料和工具来验证，包括一张工作纸、一个可推拉长方形框架、剪刀、尺子和格子图等工具。

师：比比看，哪位同学或哪组最快？遇到困难的可以举手示意！

（学生利用各种工具进行研究）

师：谁来分享一下你们的想法？

生：我认为平行四边形的面积不等于a乘b，因为在拖动过程中虽然四条边的长度不变，但平行四边形的面积变小了，你看，如果把它继续往下推，它就越来越矮，面积就会变得越来越小了。（继续往下推）这样就更小了。

生：但是我把平行四边形的框架只推一点点，就像黑板上的这样，它的面积好像没有变小啊！

生：它的面积在逐渐变小，但我也说不清楚。

师：有补充吗？

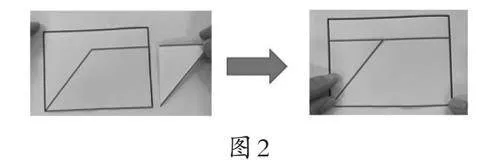
生：我知道，我们刚才不仅用了推拉的办法，还把右边的三角形剪下来补到左边的这个缺口这里，就知道它的面积少了上面一块。（学生演示，如图2）

师：了不起的方法！不仅比较出面积变小了，还发现了这个平行四边形的面积就是这么大。

师：把长方形框架推一推，推成平行四边形后，它的面积就会改变，所以平行四边形的面积不等于原来长方形的面积，不能用两条邻边的长度相乘求出平行四边形的面积，第一种猜想不正确。

【思考】好学具不仅是学习的一种道具，而且是学生思维的触发器，更是推动探索走向深入的重要支架。通过提供多种学具，给学生提供了更大的探索空间，特别是创新学具“推拉框架”和“特制卡纸”的介入，“动静学具”互相辅助，“推拉剪拼”协同探索，让学生更直观地理解面积的变化，有效消除知识负迁移的影响，促进批判思维和推理思维的发展。

2.深化验证，“探”出模型。

师：第二种猜想对吗？请在小组内继续验证，遇到困难时可以看书，也可以举手示意，开始吧！

（1）数格子验证。

生：我利用数方格的方法，先数出满格的数量，然后把这些不满格的拼成满格，这样数出格子的总数是60格，底乘高的积也等于60，所以底乘高是正确的。

师：有道理，利用了我们熟悉的数方格来证明。

（2）割补法验证。

生：我是把平行四边形沿着高（从一个顶点画出的高）剪开，把剪出来的三角形平移到另一边，拼成一个面积不变的长方形。因为拼成的长方形的面积等于平行四边形的面积，长方形的面积是10×6=60，60格，所以第二种猜想是对的。（学生展示，图略）

师：厉害！这位同学把平行四边形剪拼成长方形，这样不仅可以用数方格数出面积，也可以通过计算拼成的长方形的面积来验证。

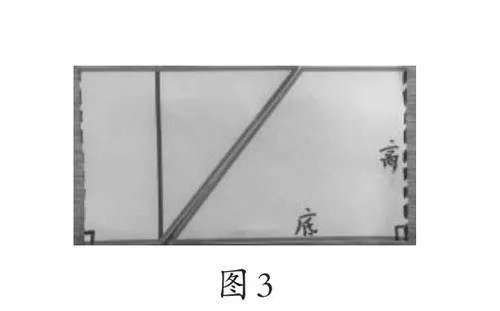
生：我也用剪拼的办法，但是我是沿着另一条高剪开，也能拼成长方形，面积也是60格。（学生展示，如图3）

【思考】建构主义学习理论认为，学生通过自己的实践和探索来构建知识。让学生开展多种方法验证的探究，从数方格到面积计算，初步建立了平行四边形面积计算的模型。

（3）深度对话，“问”出本质。

师：为什么都要沿着高来剪呢？

生：因为长方形的四个角都是直角，沿着高剪，就能剪出直角，就能拼成长方形。

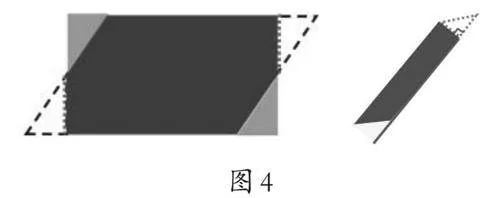
师：请看，沿着这条高行吗？这条呢？（课件出示不同的平行四边形，如图4）

生：都能拼成长方形。

师：在剪拼的过程中，什么变了，什么没变？

生：把平行四边形剪拼成长方形时，形状改变了，但是平行四边形的面积等于这个长方形的面积，面积不变。

生：把长方形框架拉成平行四边形时，形状改变了，不变的是周长，但是面积变小了，因为底的长度没变，但是高的长度变小，所以面积变小了。

师：每次都要数方格验证吗？有什么规律？

生：你看，长方形的长相当于平行四边形的底，宽相当于平行四边形的高，长方形的面积=长×宽，所以这个平行四边形的面积=底×高。（学生展示，图略）

（师生展示不同剪拼方法，也能推导出平行四边形的面积=底×高）

师：为什么要把平行四边形剪拼成长方形？

生：因为长方形的面积计算我们学过了，这样就能用旧知识来解决新问题了。

师：用旧知识来解决新问题，这就是数学中的转化思想。（板书：转化）那么，其他不同形状029eb9162ea3e1dc130c2bca4d0e867a52e3b32694234dfbe7f224f6c9065f18、不同大小的平行四边形，它的面积也是等于它的底乘高吗？（课件动态演示不同的平行四边形转化成长方形）

生：转化后，长方形的长都相当于平行四边形的底，长方形的宽都相当于平行四边形的高，再次验证了平行四边形的面积就是等于底乘高。

【思考】教之道在于导，学之道在于悟。问题与探究的最美相遇必须是思维的深度碰撞和提升。由于操作具有偶然性和模仿性，所以问题必须聚焦“为什么”开展深度对话，重点抓住学生的思考和感悟，通过观察比较，在比较中思辨，在思辨中找到“变化”中的“ 不变”，从而聚焦解决问题的本质在于转化，最后从特殊到一般推导和归纳出平行四边形的面积计算公式。

（4）整体思辨，得出结论。

师：长方形面积计算与平行四边形面积计算有什么共同点？

生：都是求面积的大小。

师：度量面积大小与度量长度有什么共同点？

生：长度是一段段地量，面积是一个方块一个方块地量。

师：所谓“万物可量”，度量长度和面积的道理是相同的，都是求含有多少个计量单位，长度是一维度量单位的累加，面积是二维度量单位的累加。面积计算公式的本质就是快速求出一共有多少个面积单位，例如把每行面积单位的数量乘行数。

【思考】笔者基于“图形的认识与测量”主题提炼出“计量单位的累加”这个大概念，明线是以此来联通整个多边形面积计算的知识结构，初步搭建长度、面积和体积计算的知识框架，暗线是解决问题策略的经验积累。

四、应用点活——回归本质，活用模型

1.基础巩固。求出这个平行四边形的面积。（图略）

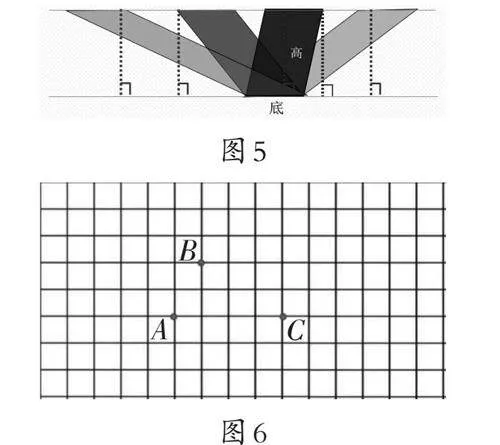
2.能力培养。比较下列平行四边形的面积大小。（如图5）

3.素养提升。平行四边形有4个顶点，点D可能在哪里？点D位置不同，平行四边形的面积会变化吗？（如图6）

学生先独立解答，再全班分享交流：第2题，为什么面积不变？第3题，点D的位置有三种情况，为什么面积都不变？

4.学习评价：（如表1）

【思考】素养习得的其中一个标准是学生在新情境中能运用已有思想和能力解决问题。四个层次的练习和评价层层递进，特别是第3题，评价重点有三点：一是结合平行四边形的特点确定点D的位置；二是发散思维找全三种情况；三是结合转化思想判断面积是否变化，同时初步渗透了三角形面积计算公式的推导。以上设计能有效评价教师的教和学生的学是否达到了以大概念为核心的单元整体教学的目标。

【本课例曾在广东省首届青年教师能力大赛中展示并获得一等奖；同时在全国青年教师能力大赛教学设计评比环节中作为10个课例之一参与评比，最终综合成绩获得一等奖】

（作者单位：广东江门市紫茶小学） J