单元统整，表征联结，由繁入简，理法融通

在竖式的教学中，我们往往直达教材中的竖式，这样的教学方式不利于算法、算理的融通。本文以“多位数乘一位数”的竖式教学为例，在梳理学生乘法竖式学习困难原因的基础上，谈谈如何通过对算理的理解、搭建学习支架促进乘法竖式的意义建构。

一、学生学习乘法竖式困难的原因分析

“多位数乘一位数”的竖式与学生已经掌握的整数加减法竖式有较大的不同，计算时，不是相同数位上的数相乘，而是要用一位数分别乘多位数中的每一位，再把乘得的积相加。这对第一次接触乘法竖式的学生来说，是一个较大的转变，所以本单元教学的重点和难点是要让学生真正理解为什么要这样算、这样算所表示的意义是什么。

在现实课堂教学中，我们总能看到教师将竖式演算的过程直接示范、学生按照制定的法则对数字符号进行机械操作的现象，出现这种现象的原因至少有三点。

第一，竖式是因满足人的某种习惯或数学自身发展的需要做出的“人为规定”，是最大程度压缩步骤和尽可能保留过程的需求中形成的平衡，所以高度简捷而规范的“竖式”算法往往不是最容易理解的形式。

第二，教材先编排口算，再编排笔算，当学生学习竖式笔算时，已经会用口算熟练算出得数，导致竖式计算时出现了先有计算结果、再有形式过程的现象，没有将竖式记录算的过程与计算的思考过程关联。这样的会用竖式计算并不是真正基于算理理解的算法掌握。

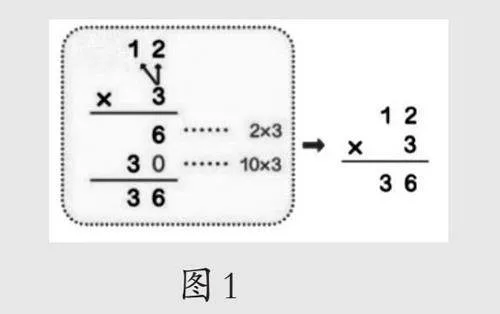
第三，教师在处理竖式教学时，为了快速求得结果而更注重算法，缺少对竖式计算合理性的思考、对运算逻辑的联系沟通。比如两位数乘一位数的竖式，教材编排了竖式详细的展开过程与压缩过程（如图1），即从长竖式到标准竖式简化的过程。但在实际教学中，教师没有理解长竖式的重要性，有的直接省略不教，有的简单呈现长竖式后就第一时间引导学生“感悟”：这个竖式是不是有点麻烦？于是迫不及待地将其改造成标准竖式，即从算理的直观立即进入了算法的抽象，忽略了长竖式的功能和长竖式到标准竖式的创造过程。

总之，竖式计算“困难”，既有知识本身、教材编排的客观原因，也有教学过程中的主观原因。

二、重组教材，设计新的教学路径

对于“多位数乘一位数”，教材上一般都是先编排口算乘法，再安排笔算乘法。这样看似衔接紧密的安排，却将算理和算法割裂在两个阶段教学。通常将算法理解为诸如竖式等标准算法，一般在笔算中教学，而算理通常理解为这个标准能够实施的理由，一般安排在口算中完成。从学科的逻辑看，算理的理解和算法的掌握是一个不可分割的整体，不管是口算乘法，还是笔算乘法，它们都是源于对数的意义与运算意义的理解，都是基于计数单位将数拆分后利用乘法口诀进行运算。所以设想以单元整体视角对教材进行有机整合、合理优化和灵活应用，将口算和笔算合并教学，算理和算法融合推进，以算理理解促进算法意义建构。为此做了如下思考：

（一）计数单位核心统领。

整数的四则运算特别强调“计数单位”，所有运算都是基于“计数单位”展开的：加（减）是相同计数单位上的数累加（减），乘法是计数单位的倍增，除法是计数单位的细分。在乘法“计数单位倍增”的算理中，主要包含了“计数单位”和“计数单位个数计数”两个维度。乘法运算的本质是同数连加，在整数乘法运算体系中，同数连加从“逐一计数”扩展到“按群计数”。如计算：2×3、20×3、200×3，就是2个一连续加了3次、2个十连续加了3次、2个百连续加了3次，它们的计数单位分别是一、十、百，口诀“二三得六”算出的是计数单位的个数。

（二）“先分后合”贯通算理。

两位数乘一位数是整数乘法运算的核心，对笔算乘法算理的理解具有“开启”的意义和迁移作用。在理解算理、探寻算法的过程中，要帮助学生从应用乘法口诀直接计算过渡到“先分后合”的一般算法。首先，学生通过对乘法的意义和数的意义的理解，完成对两位数的拆分，将两位数乘一位数转化为一位数乘一位数或整十数乘一位数，将新的运算转化成已经学过的运算。接着，引导学生在多样的拆分中体会整十数拆法具有普适性，体会十进制及位值制在运算中的价值。最后，将两位数扩展到多位数，让学生进一步应用位值原理将多位数乘一位数转化成每个数位上的计数单位与一位数相乘，再把所得的结果相加，从而指向“相同计数单位个数的累加”的运算本质。

（三）长竖式记录统整算法。

长竖式不仅体现算理，还体现竖式记录分步计算结果的功能，所以在教学中设想将长竖式记录提前至理解算理的第一节课，要求学生用长竖式将计算的过程记录下来，并通过长竖式与学生计算方法的联系，结合直观的算理理解，体会长竖式的价值。通过对教材适当重组，不区分口算与笔算，按“算理理解—长竖式记录算法—标准竖式记录算法”的流程推进教学。在设计学习材料时，选择更能体现乘法计算全过程、更具有普适性的进位乘法“14×3”作为第一次学习的材料，将不进位乘法“12×3”作为一个特例让学生自悟。教学时，先将长竖式作为一个学习乘法的支架记录完整“乘”的过程，再用长竖式记录两位数乘一位数时获得的学习经验理解多位数乘一位数、因数中间有0或末尾有0的乘法。当学生对长竖式充分感悟后自发对长竖式进行简化创造，进而形成标准的竖式。

基于以上分析，对“多位数乘一位数”的单元教学内容安排做了适度调整，形成本单元教学的整合框架，划分为7个课时（不含练习课）：（1）有关0的乘法和整十、整百数乘一位数；（2）两位数乘一位数的算理与用长竖式记录算的方法；（3）多位数乘一位数的算理与用长竖式记录算的方法；（4）（5）长竖式到标准竖式的简化，总结多位数乘一位数的算法；（6）用长竖式指导因数中间或末尾有0的乘法；（7）用长竖式指导多位数乘一位数的灵活计算（拓展）。

三、教学实践

关键课例1：表征联结，“用长竖式记录两位数乘一位数”理法统整。

乘法是依据位值原则、数的组成与分解、运算规律和性质，通过阿拉伯数字和符号书写进行的一种演算。教学中，首先，要让学生根据数的结构和算式的意义用自己的方法进行探究；然后引导学生经历对比、表达、多元表征的全过程，理解不同方法的共性，进而提炼出通法；其次，在理解算理的基础上指导学生用长竖式将算法记录下来，并通过对情境意义、计算过程、长竖式记录这三者的关联，使这个长竖式记录变得有意义；最后，通过直观表征、加法原则、乘法原则、长竖式表征将位值概念与乘法竖式每一部分的结果建立联结，既能深化学生对算理的理解，又能提高学生的运算能力。

（一）从数到算，体验从“自由拆分”到“按十进制拆分”的计算方法。

1.师：（出示点子图，图略）运动会上，301班排队入场，你能数出这个班一共有多少人吗？

学生先数出每行有14人，有3行，再列出算式：14×3。

2.师：这是两位数乘一位数的乘法（板书课题），乘法口诀表里没有这样的口诀可以直接求，你能想办法求出这道题的答案吗？把你求的过程记录下来，并在点子图上圈一圈，表示出你的思路。

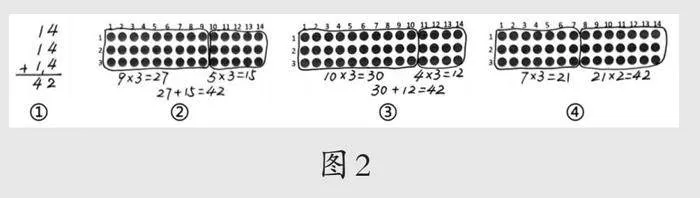
3.反馈学生作品（如图2）。

（1）针对方法①，得出可以根据乘法的意义，理解“14×3”表示3个14的和，转化成同数连加求得结果。

（2）以方法②为例，“14”去哪里了？为什么要这么拆分？拆分后每一步乘得的积表示哪一部分？最后为什么又要加起来？

从学生的回答中得出，因为14×3乘法口诀表里没有，把它变成口诀可以计算的“9×3＝27”，再求出剩余的“5×3＝15”，最后把这两部分加起来，引出“先分后合”的计算方法和“将新问题转化为旧知识”的数学思想。

（3）方法②到④你都看得懂吗？比一比这三种方法，有什么相同和不同？

（4）这三种方法都用到了“拆分—乘—加”的方法，你觉得哪一种拆分的方法可以作为两位数乘一位数普遍适用的方法？

得出：在计算两位数乘一位数时，可以将两位数按数的组成拆分成“几十加几”，比如：14里面有1个十和4个一，求3个14就是先求出3个10是30、3个4是12，再把30和12合起来，像方法③那样用三步计算，这样的记录方法叫作“横式记录”。

（二）多元表征，理解两位数乘一位数的算理。

1.用连加计算的方法其实和哪种拆分是一致的？

学生发现连加算式和方法③其实是一致的，都是分别算出3个4和3个10是多少，再求和。

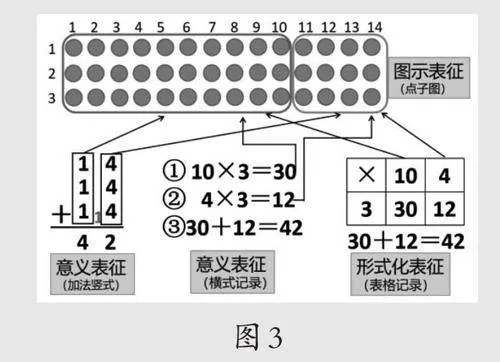
2.把乘法三步计算与连加算式联系起来，并与直观图联系（如图3），寻找每一步的具体意义，并伺机出示表格记录。

（三）搭建支架，用长竖式记录算的过程。

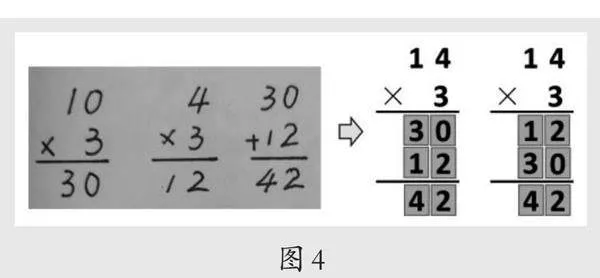
1.师：你能用竖式将计算“14×3”的过程记录下来吗？

出示学生列出的三个竖式（如图4），学生在教师引导下将三个竖式合并成一个长竖式，发现两位数乘一位数可以看成几个几十和几个几来算，可以从高位算起，也可以从低位算起，和运算的顺序无关。

2.长竖式中的每一个数在不同表征中的意义。

（1）追问：这个长竖式中的“30”是怎么得来的？口诀“一三得三”，算出来的为什么是“30”而不是“3”？下面这条横线表示什么意思？“42”又是怎么得来的？

（2）对长竖式中的“30”“12”“42”，分别在横式记录、加法竖式、表格记录、点子图中寻找意义联结。

3.比较竖式加法和竖式乘法。

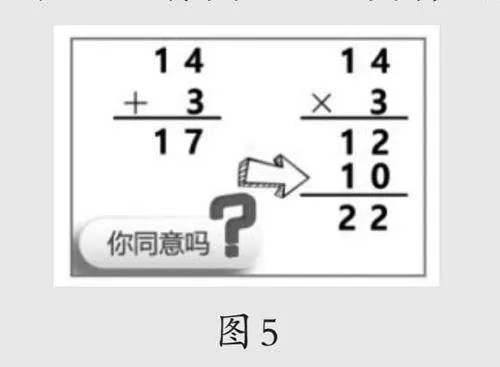
师：（出示图5）有人说计算“14＋3”时，只要把个位上的4和3相加得7，第二个加数十位上没有，所以十位上的1直接移下来，14＋3＝17；计算“14×3”时，个位上的4×3＝12，第二个乘数十位上也没有，所以只要十位上的1直接移下来再相加……你同意吗？为什么？

通过点子图直观演示，发现加法算式表示第一行有14个点子，第二行有3个点子，而乘法中的“3”表示14的个数，需要求出“3个4”和“3个10”的和，所以“要先用3乘14的每一位，再把两次乘得的积合起来”。

（四）突出位值，用长竖式统整算理与算法。

1.表征。出示算式23×4和32×4，请学生用小棒图表示这两个算式所表示的意义。

2.尝试。先想一想分别怎么算，再用长竖式记录算的过程。

3.比较。（1）计算这两道题，你们分别乘了几次？两道题都用了“二四得八”这句口诀，在这两个算式里表示的意思一样吗？你能在小棒图中分别指一指吗？（2）这两道题计算“3×4”时，为什么一道表示“12个十”，一道表示“12个一”，谁决定了这样不同的结果？

4.归纳。用长竖式记录这三道题的计算过程时，有什么相同点？从而得出两位数乘一位数“□□×□”的计算模型，并板书：用一位数乘两位数的每一位，再把得到的积相加。

关键课例2：由繁入简，“多位数乘一位数”理法融通。

长竖式记录是源于学生对算理充分理解后的记录与创造，而标准竖式是一种规定，规定的得来需要充分的理由，但教材仅仅借助学生的对话“还可以列竖式计算”规范了竖式的书写格式，显然，这样的告知掩盖了规定背后的道理。所以等学生掌握用长竖式记录计算过程后，应安排简化到标准竖式的创造活动，具体做好以下三点：

（一）明白哪里可以省略。

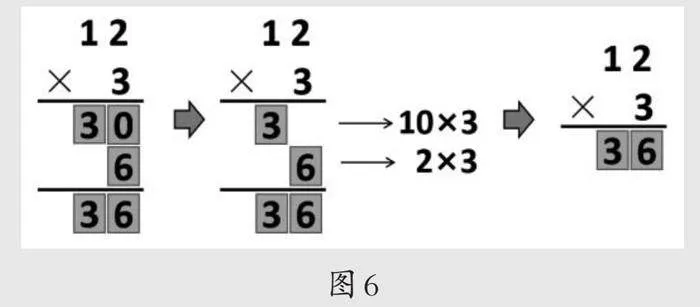
让学生用数字卡片贴出计算12×3的长竖式（如图6），教师引导：数学的记录既追求清楚，又强调简单，如果把这个长竖式写得简单些，你觉得哪些地方可以省略不写？理由是什么？学生自然能想到计算十位时，一三得三，只要把“3”写在十位就表示3个十，个位上的0可以省略，然后长竖式出现了一个“不稳定”的结构，学生就把十位上的3和个位上的6摆在一起，舍去重复的部分，标准竖式应运而生。

（二）结构化的表征促进标准竖式的建构。

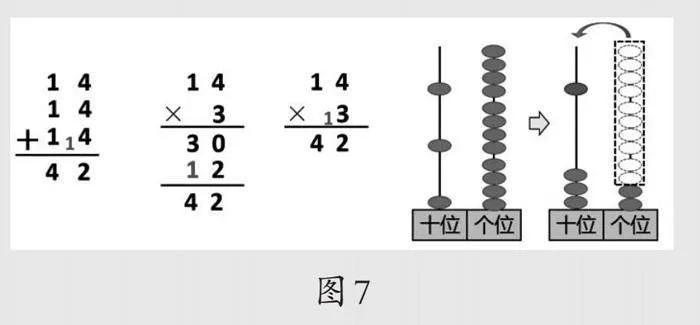
当学生理解了标准竖式计算后，及时出示14×3，引导学生先用长竖式计算，再试着用标准竖式计算，然后用计数器拨出14×3的计算过程，从而理解标准竖式的算理（如图7），最后联系标准算式、连加算式、长竖式和计数器理解积十位上“4”的由来、个位进上来的“1”在不同表征中的意义，真正理解标准竖式背后的道理。

（三）讨论从哪一位算起。

乘法的本质与运算的顺序无关，反映在长竖式上既可以从高位算起，又可以从低位算起。学习了标准竖式后，及时设计一道进位乘法题，让学生尝试、比较、讨论：从哪一位算起？学生很容易感受到在计算进位乘法时从低位算起的简洁方便。

“多位数乘一位数”实现了从表内乘法求积到基于位值的乘法竖式求积的飞跃，是培养学生运算能力的关键时期。教学中，我们应该从单元整体视角出发，以计数单位的计数为核心，在多元表征的联系中理解算理，以蕴含着抽象算理、直观算法的长竖式为学习支架记录算的过程，在长竖式的压缩过程中实现标准竖式的创造与建构，为后续整数、小数竖式学习提供理解与迁移的源泉。

参考文献：

[1]何晴，刘莹.“竖式”的知识属性[J]. 教学月刊（小学版·数学），2021（1/2）：4-7.

[2]马云鹏，吴正宪.深度学习：走向核心素养[M].北京：教育科学出版社，2019：91-94.

[3]章勤琼，杜依铭.运算教学中如何做到“法理兼顾”：略谈运算教学的三个要点[J].福建教育，2022（10）：28-31.

[4]宋煜阳.基于数和运算意义的乘法算理整体性理解[J].教育视界，2022（2）：9-11.

（作者单位：浙江杭州市临平区文正小学） H