巧设问题串 凸显“一致性”

一、创设情境，引发冲突[ ]

师：周末，乐乐到超市为家人采购面包。甲种面包他买了2个，花了13元；乙种面包他买了4个，花了25元。乐乐非常善于思考和提问，同学们猜猜，他会提什么问题呢？

生：哪种面包更贵些？

师：想知道哪种面包更贵些，应该先求出什么？

生：两种面包的单价。

师：请同学们跟老师一起列式求出两种面包的单价分别是多少。（如图1）

师：从刚才的计算中，我们发现两种面包的单价都是6元余1元，同学们说哪种面包更贵些呢？

生：一样贵。

师：大家都同意两种面包一样贵吗？

生：不一样贵。求甲种面包的单价时是平均分成2份，而求乙种面包的单价时是平均分成4份，如果将余下的1元继续分下去的话，得到的结果并不一样。

师：你非常善于观察和分析，从表面的相同看到了背后的不同！因为余下的1元没有继续分下去，目前所得的商的精确度是不够的。

【评析】从真情实境中抽象出数学问题，符合学生的认知，也有助于激发学生进一步探究的兴趣，让其感受数学源于生活，又服务于生活。创造认知冲突，就会引发学生进一步思考：以前学的有余数除法所得的商的精确度不够，应该将余下的1元继续分，从而体会小数除法产生的必要性。

二、多元表征，感悟一致

师：看来，现在问题的关键就是如何将余下的1元继续分下去。请同学们先集中精力思考：求甲种面包单价时，余下的1元该怎么分呢？可以算一算、写一写，也可以画一画、分一分。

（完成后，以小组为单位进行交流和汇报展示）

生：人民币单位换算。（如图2）

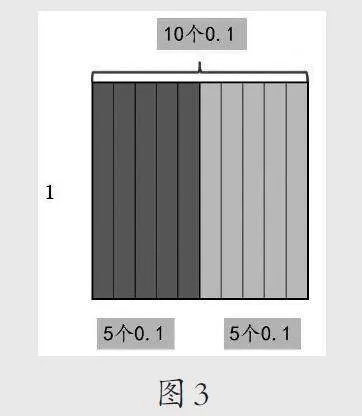
生：计数单位换算。（如图3）

师：两位同学分的方法不同，但殊途同归，都分得非常精彩！如果将这两种分法放在一起，仔细观察，大家能发现有什么相同之处呢？

生：都是从“1”到“10”。

生：都是从大单位转化成了小单位。

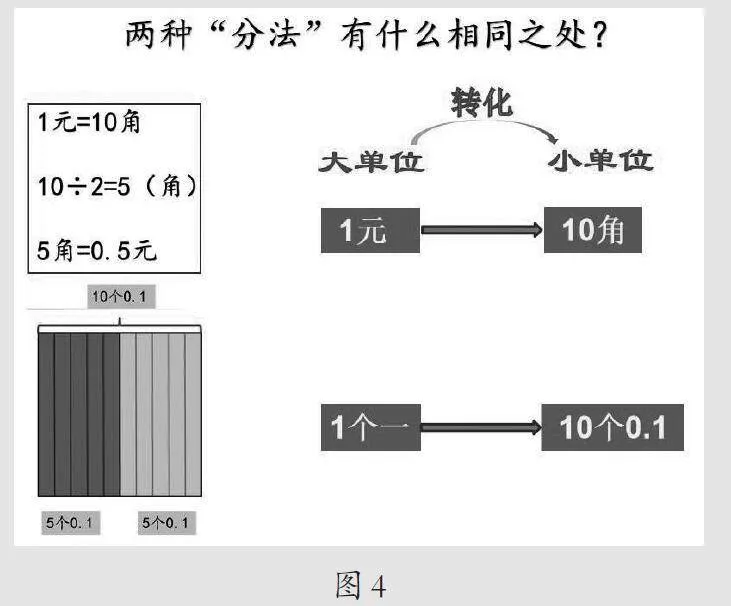
师：同学们不但有一双慧眼，还有很强的总结概括能力！人民币单位换算，是将1元转化成了10角；计数单位换算，是将1个一转化成了10个0.1。当大单位不够分时，就将大单位转化成小单位，从而继续分下去。（如图4）

【评析】教师借助“1元该怎么分呢”这一问题引发学生的思考走向深入，引导学生经历“人民币单位转化”和“计数单位转化”等多种表征。借助“两种分法有什么相同之处”这一问题，让学生在寻找共同点的过程中感悟表征方式的内在一致性：都是将不够分的大单位转化成小单位，从而继续分下去，为引出小数除法的竖式奠定基础。

三、深入探究，凸显本质

（一）沟通算理，感悟“一致”。

师：既然同学们对“分”的过程有了很深的领悟，那现在大家能把这个过程在原来竖式的基础上接着进行记录吗？请继续完成甲种面包单价的计算并讲一讲计算的道理。

生：在“1”的后面添上“0”，也就是将1元转化成10角，平均分成2份，每份是5角，即0.5元。

生：在“1”的后面添上“0”，也就是将1个一转化成10个0.1，平均分成2份，每份是5个0.1，即0.5。

师：同学们还有什么问题要问吗？

生：为什么要在“1”的后面添上“0”？

生：为什么小数点要点在“6”和“5”之间？

师：两位同学的问题都非常有研究价值。哪位同学能做出解答？

生：当大单位不够分时，将大单位转化成小单位，就可以继续分下去；10个0.1平均分成2份，每份是5个0.1，而要表示出5个0.1，“5”就应该商在十分位上，小数点也就必须点在“6”和“5”之间。

师：数学就是这样一门“讲理”的学科，在刚才的交流碰撞中，同学们将其中的道理越讲越明，越说越透！

【评析】借助学生的提问“为什么要在‘1’的后面添上‘0’”“为什么小数点要点在‘6’和‘5’之间”，教师引导学生将“分”的过程与竖式表征对应起来，理解添“0”就是为了将大单位转化为小单位才能继续分的道理。感悟除法运算就是从分计数单位“1”到分计数单位“0.1”，再到分计数单位“0.01”……这一不断细分的过程，而小数点是计数单位“1”和计数单位“0.1”的分界。

师：甲种面包的单价已经解决了，现在大家能够按照刚才的思路求出乙种面包的单价吗？请同学们独立完成并尝试从“计数单位”的角度解释每一步竖式计算的道理。

生：2个十平均分成4份，不够分，将其转化成20个一；20个一与5个一合起来是25个一，平均分成4份，每份是6个一，余下了1个一；将余下的1个一转化成10个0.1，平均分成4份，每份是2个0.1，余下了2个0.1；再将余下的2个0.1转化成20个0.01，平均分成4份，每份是5个0.01，最后求得乙种面包的单价是6.25元。

师：6.5元＞6.25元，可以判断出甲种面包更贵些。其实，刚才在计算两种面包的单价时，同学们已经不自觉地学会了小数除法。现在请大家整体观察这两个竖式计算的过程，谁能说说小数除法与整数除法有什么内在联系吗？

生：小数除法是从整数除法“生”出来的。

生：都是将计数单位不断地“分”。

师：同学们已经抓住了除法的本质。确实，小数除法是在有余数除法的基础上“生长”出来的，不论是整数除法还是小数除法，都是计数单位的细分，当大单位不够分时，就将大单位转化成相邻的小单位，再继续分。

【评析】借助“小数除法与整数除法有什么内在联系”这一问题，教师引导学生在沟通交流的过程中，明确了小数除法是在有余数除法的基础上“生长”出来的；无论是整数除法还是小数除法都是从高位到低位，一位一位地分，当遇到不够分时，就将大单位转化为相邻的小单位继续分，充分体会“计数单位的不断细分”这一本质。

（二）对比分析，总结算法。

师：求甲、乙两种面包的单价时，我们算的是整数除以整数商是小数的除法，现在有两道小数除以整数的计算（9.84÷3、6.4÷5），同学们会做吗？请大家独立完成。完成后，依然要从“计数单位”的角度解释竖式每一步计算的道理。

生：第一题，9个一平均分成3份，每份是3个一；8个0.1平均分成3份，每份是2个0.1，还余下2个0.1；将余下的2个0.1转化成20个0.01，与4个0.01合起来是24个0.01，将24个0.01平均分成3份，每份是8个0.01；最后的结果是3.28。第二题，6个一平均分成5份，每份是1个一，余下了1个一；将余下的1个一转化成10个0.1，与4个0.1合起来是14个0.1，14个0.1平均分成5份，每份是2个0.1，余下4个0.1；将余下的4个0.1转化成40个0.01，平均分成5份，每份是8个0.01，最后的结果是1.28。

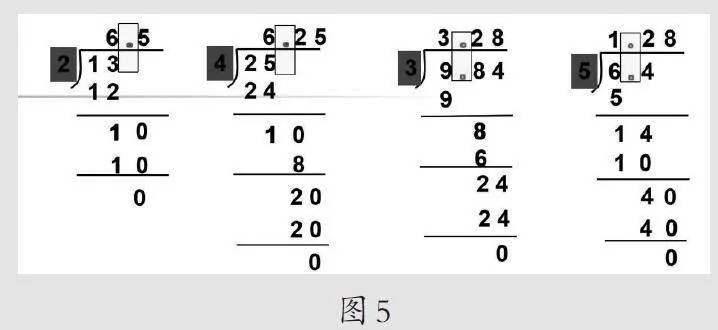
师：现在我们将刚刚完成的四道小数除法放在一起，仔细观察它们的除数都是什么数。（如图5）

生：整数。

师：这节课我们重点学习的就是“除数是整数的小数除法”。结合这四个除法算式，你能说一说“除数是整数的小数除法”的计算方法吗？

生：按照整数除法的方法来计算。

生：当大单位不够分时，转化成小单位再分。

生：商的小数点与被除数的小数点对齐。

师：同学们总结得非常好！按照整数除法的方法来计算，从高位开始，将计数单位不断细分，当遇到大单位不够分时，就将其转化成相邻的小单位继续分，商的小数点要与被除数的小数点对齐！

【评析】有了前面几个问题的铺垫，教师再抛出问题：“结合这四个除法算式，你能说一说‘除数是整数的小数除法’的计算方法吗？”因为学生对小数除法的算理有了深度理解，在此基础上总结出除数是整数的小数除法的计算方法就变得水到渠成。

四、总结梳理，拓展延伸

师：同学们，这节课已接近尾声了。学完这节课，你有哪些收获？

生：学会了除数是整数的小数除法的计算方法。

生：理解了除法的本质就是计数单位的细分。

……

师：今天学习了除数是整数的小数除法，想一想，接下来我们会研究哪一类小数除法？

生：除数是小数的除法。

师：课后，希望同学们在本课学习的基础上，继续研究除数是小数的除法。

【评析】教师引导学生回顾所学，有助于建构知识体系。另外，学习由课上延伸到了课后，学生的思维得到进一步提升，为后面的学习做好铺垫。

【总评】

1.巧妙创设情境，引发学生对除法的认知冲突。

创设生活情境：周末，乐乐到超市为家人采购面包。甲种面包他买了2个，花了13元；乙种面包他买了4个，花了25元。学生提出问题：哪种面包更贵些？大家都会先想到分别求出两种面包的单价，再做比较。

绝大部分的学生会认为甲种面包的单价=乙种面包的单价，两种面包一样贵。此时进行适当留白，有学生就会意识到因为1元没有继续分完，还不能这么早下结论。这也就会引发学生进一步思考：以前学的有余数除法所得的商的精确度不够，应该将余下的1元继续分，从而体会小数除法产生的必要性。

借助具体的生活情境，在整数除法和小数除法的连接点处（有余数的除法）制造冲突，能够让学生充分感悟计数单位进一步细分的意义——有助于提高精确度。

2.精心设计“问题串”，促进学生对除法本质的理解。

好的问题能够不断打破学生原有的认知平衡，激发学生的探究欲望。皮亚杰指出，只有学生自我发现的东西才能积极地被同化，从而让学生产生深刻理解。本节课，在紧密联系的“问题串”的驱动下，学生探究热情高涨，思维逐渐向纵深发展。

问题一：求甲种面包的单价，余下的1元该怎么分呢？

借助“1元该怎么分呢”这一问题让学生感悟继续分的必要性，引发思考和探究，引导学生经历“人民币单位转化”和“计数单位转化”等多种表征，从而加深理解。

问题二：两种“分法”有什么相同之处？

借助“两种‘分法’有什么相同之处”这一问题，让学生在寻找共同点的过程中感悟表征方式的内在一致性：都是将不够分的大单位转化成小单位，从而继续分下去，为引出小数除法的竖式奠定基础。

问题三：为什么要在“1”的后面添上“0”？为什么小数点要点在“6”和“5”之间？

引导学生将“分”的过程与竖式表征对应起来，理解添“0”就是为了将大单位转化为小单位才能继续分的道理；在单位不断细分的过程中，确定商的小数点的位置。

问题四：小数除法与之前学过的整数除法有什么内在联系？

借助这一问题，引导学生在沟通交流的过程中，明确了小数除法是在有余数除法的基础上发展而来的，打通了联系，无论是整数除法还是小数除法本质都是“计数单位的不断细分”。

问题五：如何计算除数是整数的小数除法？

有了前面几个问题的铺垫，学生对小数除法的算理就有了深度理解。在此基础上总结出除数是整数的小数除法的计算方法，让学生进一步体会整数除法与小数除法的一致性就变得水到渠成。

总之，在富有启发性的“问题串”的驱动下，学生借助多元表征直观理解计数单位细分的过程，感悟小数除法与整数除法运算的一致性。除法的本质就是计数单位的细分，当大的计数单位不够分时，就将其转化成小的计数单位，继续分；同时，在计数单位细分的过程中，学生也能体会到数意义与数运算的一致性，即数意义是数运算的基础，数运算是对数意义的再解读，最终实现对运算能力和推理意识等核心素养的培养。

【本文系2023年度青岛西海岸新区教育科学“十四五”规划课题“指向数学核心素养提升的小学‘数与运算’结构化教学实践研究”（课题编号：QXJK145D144）的阶段性研究成果之一】

（作者单位：山东青岛市西海岸新区兰亭小学，江苏无锡市通德桥教育集团）