凸显核心知识联结 指向高阶思维发展

一、激活经验，在知识连续中生成探究情意

师：同学们，这节课我们一起研究——（出示课题：3的倍数的特征）之前，我们有没有研究过这样的同类问题呢？

生：我们已经研究过2、5的倍数的特征。

师：2、5的倍数有怎样的特征呢？

（学生答略）

师：还记得是怎样探究它们的特征吗？

生：我们是先在百数表中找到2或者5的倍数进行观察，得到猜想，再举例进行验证，发现符合猜想，就得到了结论。

师：现在要研究的3的倍数又会有怎样的特征呢？先来猜一猜。

二、猜想验证，在批判理解中丰富探究经验

1.首猜得法。

生：我觉得3的倍数个位上可能是0、3、6、9。

师：能说说你是怎么想到这样猜的吗？

生：因为2的倍数和5的倍数都只要看个位就能判断，所以我感觉是看个位猜。

师：看来是受到之前2、5的倍数的特征的影响。其他同学，你们也支持这个猜想吗？

生：我反对，3的倍数有些是12、15、18这样的，它们的个位就不是3、6、9、0。

师：这位同学真有经验，看到猜想，立刻想到举例验证，而且举出了像12、15、18等这些不符合猜想的反例。（板书：举例，反例，正例）有不符合猜想的反例，那有没有符合猜想的正例呢？

生：有的，比如3、6、9、30、33、36、39，它们个位上就是3、6、9、0。

师：一下子举出了这么多正例，你们为什么还要反对这个猜想呢？

生：因为只要有一例反例，这个猜想就是错误的。

师：我们一起回头看看，之前探究2、5的倍数的特征，猜想时还伴随着——（学生回答：观察）现在探究3的倍数的特征，为了获得合理的猜想，你有什么好的建议吗？

生：我们也可以先到百数表中圈出3的倍数，观察观察再猜。

（学生在百数表中圈3的倍数，集体校对并改正圈的结果）

师：一起看百数表中3的倍数，现在还坚定地认为从个位能找到3的倍数的同学举手示意下。（没人举手）一看百数表，怎么都认为看个位找不到3的倍数的特征了呢？

生：因为这些3的倍数的个位出现了0、1、2、3、4、5、6、7、8、9，辨别不出来了。

2.再猜明理。

师：看个位找不到3的倍数的特征，那看什么呢？

生：看十位。

师：那就试试呗，带着刚刚的经验再看看十位，认为能找到3的倍数的特征的同学向老师点点头，认为不能的摆摆手。

（学生齐摆手）

师：你们瞧，仅看个位或仅看十位都找不到3的倍数的特征，那该怎么办呢？

生：（多数）可以个位、十位都看。

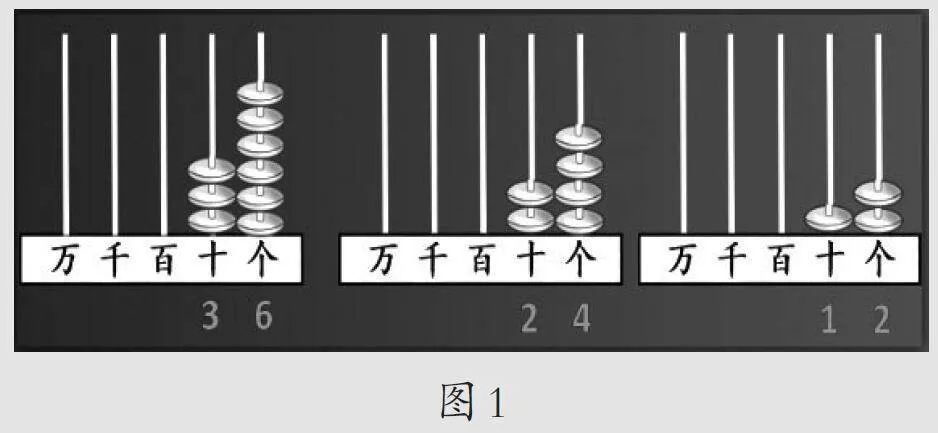
师：还是听你们的，继续观察百数表中3的倍数，个位和十位合起来看看，会不会有新发现呢？如果有困难，还可以请计数器帮忙，像这样在百数表中找一些3的倍数拨一拨（如图1），看看两个数位上的珠，会不会得到启发呢？有了发现，同桌可以先交流交流。

（学生自主探究后同桌交流，教师巡视了解情况）

师：哪位同学愿意把自己的发现和大家分享一下？

生：我通过在计数器上拨珠看到，3的倍数，个位和十位相加的和是3的倍数。

（教师记录这个猜想，学生结合电子计数器，边举例拨数边讲解）

生：我也是发现了个位和十位加起来都是3的倍数，（指百数表）比如，1和2加起来是3，是3的倍数，3和3加起来是6，是3的倍数，6和9加起来是15，也是3的倍数。

师：真得谢谢这两位小老师，都是有理有据。我们就再来看看百数表，为了让大家看得更明白，可以对它动个小手术（如图2），沿着这条线看，3的倍数个位和十位上数的和是——（生：3）这条线上3的倍数个位和十位上数的和是——（生：6）继续这样看下去，再是——（生：9、12、15、18）百数表中这些3的倍数符合你们刚刚的猜想吗？

生：都符合。

生：找不到反例。

师：这么看来，这个猜想对于百数表中的数是——（生：正确的）那对于百数表以外的数呢？想不想继续来猜猜？

生：想。

师：不过猜想还得伴随着——（生：观察）所以老师随机给你们准备了一些多位数表，3的倍数都已经圈出来了（如图3），仔细看看猜猜，有了猜想可以在四人小组里交流交流。

（学生看、猜后先小组交流，后小组汇报）

生：我们组认为3的倍数不管有多大，各位上的数加起来肯定是3的倍数。

（全班附和，教师板书“3的倍数，它各位上数的和一定是3的倍数”）

师：但这毕竟是你们观察数表获得的猜想，怎么验证呢？

生：举一些3的倍数的例子看看它们各个数位上的数加起来是不是3的倍数。

生：还要找找有没有反例。

师：大家很有经验了，老师也有个提议，大家可以同桌合作，像这样一起来验一验。

（课件出示举例验证的要求并示范，学生举例验证后，小组交流，教师巡视）

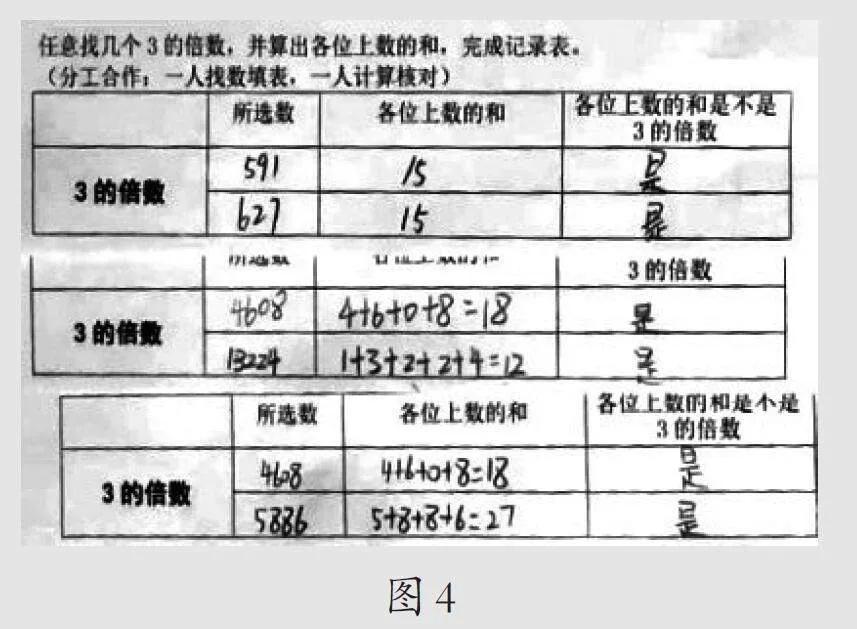
师：老师收集了一组同学的验证结果（如图4），想不想听听他们组有什么想说的？

生：（组长）我们组找的这些3的倍数，各位上的数相加起来的确是3的倍数，没有找到反例，说明猜想是对的。

师：这是他们组的验证结果，其他组呢？要不要追问一下？

生：我还要问一下其他组，有没有找到反例？

生：（齐）没有。

三、完善结论，在逻辑思考中提升思维水平

师：验证到这儿，我们初步认为这个猜想是对的，老师告诉你们吧，这的确是一条正确的结论。（移动猜想处的板书至结论处）之前百数表中的发现和这个结论比对一下，怎么样？

生：是一致的，这条讲得更全面。

（擦掉前面百数表中的发现）

师：你们看，“3的倍数，各位上数的和一定是3的倍数”，研究到这儿，还有没有其他想问的呢？

生：不是3的倍数，各位上数的和一定不是3的倍数吗？

师：那继续研究，猜想时不忘观察，还是借着数表看看猜猜吧。

（学生在小组内看、猜，获得猜想并再验证，得到结论并板书）

师：现在我们已经知道了3的倍数，各位上数的和一定是3的倍数；不是3的倍数，各位上数的和一定不是3的倍数。研究到这儿，反过来要判断一个数是否是3的倍数，你有好办法了吗？

生：我们只要看各个数位上的数加起来是不是3的倍数。

四、游戏加持，在应用内化中实现心智和谐

师引导：那就用一用你们的好办法，玩个游戏“数字翻翻乐”。

（课件出示：将分别标有数字0～9的10张卡片打乱顺序后背面朝上，请从中任意翻开3张，如果能摆出一个是3的倍数的三位数，将获得一枚幸运笑脸奖章。学生第一次翻出0、4、2这3张数字卡片，全班鼓掌）

生：我摆了402，4、0和2相加是6，是3的倍数，所以402也是3的倍数。

师：祝贺你，不仅运气好，道理讲得也好，奖励你学有所获。还想玩吗？换个要求再翻。

（课件出示：请从余下的数字卡片中任意翻开1张，如果能和前面的3张数字卡片组成一个是3的倍数的四位数，将获得一枚幸运笑脸奖章）

师：先在心里想一想，最想翻到哪个数字？

（学生第二次翻出数字8，第三次翻出数字6，全班欢呼）

师：老师刚刚看到你摆放数字6的时候犹豫了一下，最后决定放在末尾，能告诉大家为什么犹豫一下吗？

生：我觉得它还可以放在前面，应该是随便放在哪一位都可以，因为它们加起来都是12，总归会是3的倍数。

师：厉害了，对3的倍数的特征理解得这么深刻。（全班鼓掌）继续改变游戏规则，把数字卡片全打开，这10张数字卡片组成了一个十位数，它是3的倍数吗？

生：是3的倍数，10个数字和是45，45是3的倍数。

师：如果在10张数字卡片中去掉1张，使其余卡片摆成一个3的倍数，你会去掉哪张？

生：去掉0，因为去掉0剩下9个数字的和还是45。

生：去掉3、6或9也行，它们都是3的倍数，原来是3的倍数，去掉一个3的倍数，结果一定还是3的倍数。

师：你的感觉真好，一下子就把3的倍数的特征给用活了。

生：我觉得去掉1和2也行，它们加起来是3的倍数，去掉它们剩下的也是3的倍数。

师：你从去掉1个数字还讲到了去掉2个数字，不管去掉几个数字，它们背后有没有什么相同的道理呢？

生：只要去掉的数字之和也是3的倍数就可以。

师：此处该有掌声。

五、回顾反思，在结构关联中走向延伸发展

1.回顾反思，感知形式上的关联。

师：这节课我们运用之前的研究经验继续探究了3的倍数的特征，与前面探究2、5的倍数的特征相比，今天的探究过程中哪些环节给你留下了深刻印象？

生：数字翻翻乐给我留下了深刻的印象，有点烧脑。

师：嗯，带着数学思考玩游戏特别带劲。

生：举例验证让我印象深刻，要看能不能举出反例，只要有一个反例就可以推翻猜想。

师：你们的思考越来越严谨了。

生：我觉得猜想环节有点让人惊心，老是猜错，好不容易才成功。

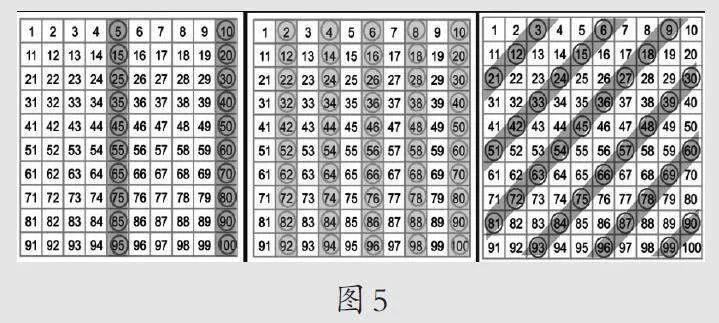
师：今天我们的猜想的确不是那么一帆风顺，让我们再回到之前的探究过程去感受感受（如图5）。百数表中5、2的倍数是——（生：竖着排的）利于我们从个位猜想它们的特征并且成功了，而3的倍数是——（生：斜着排的）看个位猜想失败了，这样的排列其实也在启发我们要换角度猜，百数表真是神奇，它是我们研究这类问题的重要工具。

2.解释说理，感悟本质上的一致性。

师：同学们，到目前为止我们已经知道判断一个数是不是2或5的倍数时只要看个位，而判断一个数是不是3的倍数时却要看——（生：各位上数的和）学到这儿，你们还有什么疑问吗？

生：为什么判断一个数是不是2或5的倍数时只要看个位，判断一个数是不是3的倍数时却要看各位上数的和呢？

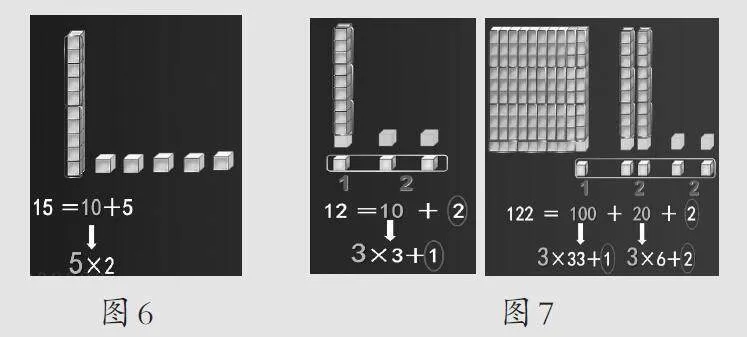
师：好问题。我们就借助图一探究竟吧。先从5的倍数开始，以15为例，这样先圈一圈（如图6），你能说一说判断时为什么只要看个位吗？

生：因为十位上的十是5的倍数，不管几个十都是5的倍数，所以只要看个位。

师：再看2的倍数，也圈一圈，道理其实是一样的。现在判断一个数是不是3的倍数，几个一圈（如图7）？

生：（齐）3个。

师：有什么发现？

生：十位上还余下1个。

生：只要把十位上余下的1个和个位上的2个合起来就是3的倍数。

师：对呀，这就是我们为什么要看这2个数位上数的和来判断的道理。再看这个三位数，继续圈圈、看看、想想，有什么想说的？

生：3个3个圈，百位上余下1个，十位上余下2个，要把百位余下的1个、十位余下的2个和个位余下的2个合起来看，不是3的倍数，所以122就不是3的倍数。

师：像这样类推到其他多位数，现在明白为什么判断一个数是不是3的倍数时要看各位上数的和了吗？（学生回答：明白）带着这些收获继续探秘数的世界吧，下课。

（作者单位：江苏宜兴市官林实验小学）