化抽象关系为可见的模型

课堂再现

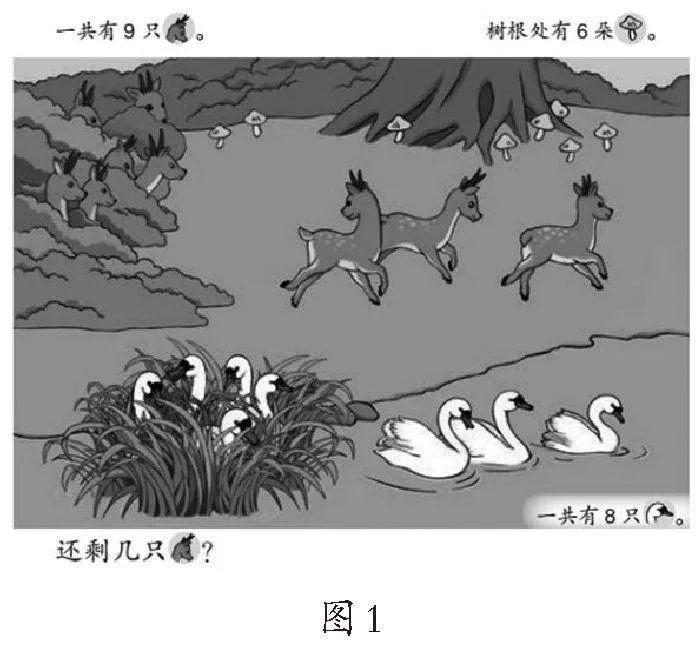
“解决问题（二）”（人教版教材一年级上册）是“认识8和9的加减法”后的一节课（如图1）。

作为教材中第二节严格意义上的有关解决问题的课，与之前有很大的不同：一是学生解决数学问题，不是从单一情境中直接利用相关信息解决问题，需要从数学元素丰富的主题图中，通过观察、分析，收集、筛选相应的数学信息；二是获取信息的方式从读图变为图文结合。

对刚入学不久的一年级学生来说，虽然通过学习已经初步知晓解决问题的步骤，即获取信息、提出问题、列式解答、检查验证，但存在这样的问题：信息获取方式单一，基本上就是看图直观地数一数；信息加工方式简单，全凭感觉或经验选择加或减的方法解决问题，因为他们还没有通过加减法的意义建立起相应的数量关系。为了解决以上问题，更好地落实教学重点、突破教学难点，笔者设计了如下教学环节。

片段一

师：（出示主题图，如图1）关于鹿，你从图中知道了什么？

生：我看到树丛中有6只鹿露出来了。

生：我看到右边有3只鹿。

生：我看到上面有个9。

师：哪里有个9？上来指一指。

（该生上台指主题图上“一共有9只鹿”中的9）

师：这句话谁看懂了？来读一读。

生：一共有9只鹿。

师：你是一个会看文字的小朋友，真了不起。除了这个信息，从图上我们还能一眼看出来的信息是什么？

生：我还看到有3只鹿。

师：我们刚刚找到了两个信息，老师把它们请到黑板上。

（板贴：一共有9只，跑走了3只）

师：信息找到了，那你能根据信息提出什么数学问题呢？

生：一共有9只，跑走了3只，还剩几只呢？

师：他用“还剩”提问题，非常好。谁能像他一样提出问题？

（教师请了3个学生重复提问题，并板贴呈现，全班齐读）

师：之前我们学过大括号，谁还记得大括号表示什么意思呢？

生：大括号表示把它们合起来。

师：真棒，还能加上动作。那现在，李老师想把我们找到的信息和问题放在大括号上，你觉得“一共有9只”该摆在什么位置？

（学生上台移动板贴，摆在了大括号的右边）

师：说说你的理由。

生：大括号表示合起来，合起来有9只，所以摆在这里。

师：有没有不同意见？

（学生上台移动板贴，摆在了大括号的左边）

师：那你觉得另外两条应该摆在哪？

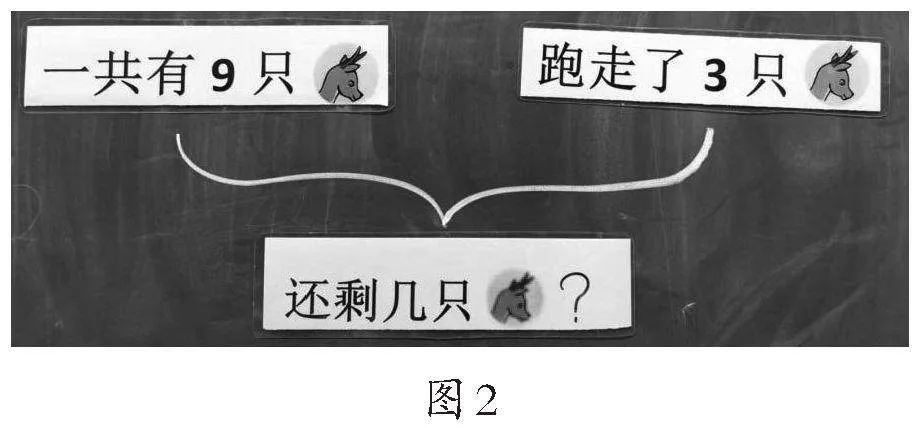
（学生把“跑走了3只”摆在了右边，把“还剩几只”摆在了大括号的下面。如图2）

师：说说看，你为什么这么摆？

生：原来一共有9只，跑走了3只，所以还剩下的就摆在了下面。

师：喔，原来你是这样想的。谁有和他不一样的想法？

（另一个学生上来，把“一共有9只”和“还剩几只”两张卡片交换了位置）

师：说说你是怎么想的。

生：因为大括号表示合起来的，所以“一共有9只”应该摆在这里。

师：大括号表示合起来一共有多少，所以“一共有9只”摆在大括号的外面。真好，你们能把题目中的信息与之前学过的数学符号结合起来。

片段二

（学生列出9-3=6的算式，教师引导学生分析算式中每个数的意思后，提问：为什么用减法）

生：因为问号在大括号的里面。

师：哦，能用问号的位置来解释。问号在大括号的里面，就表示问题求的是一部分，所以用减法来做。还有呢？

生：因为是跑走了3只，所以用减法。

师：我们说减法表示把一个整体分开，从里面拿走一部分。“跑走”也就是从里面拿走，所以用减法。

片段三

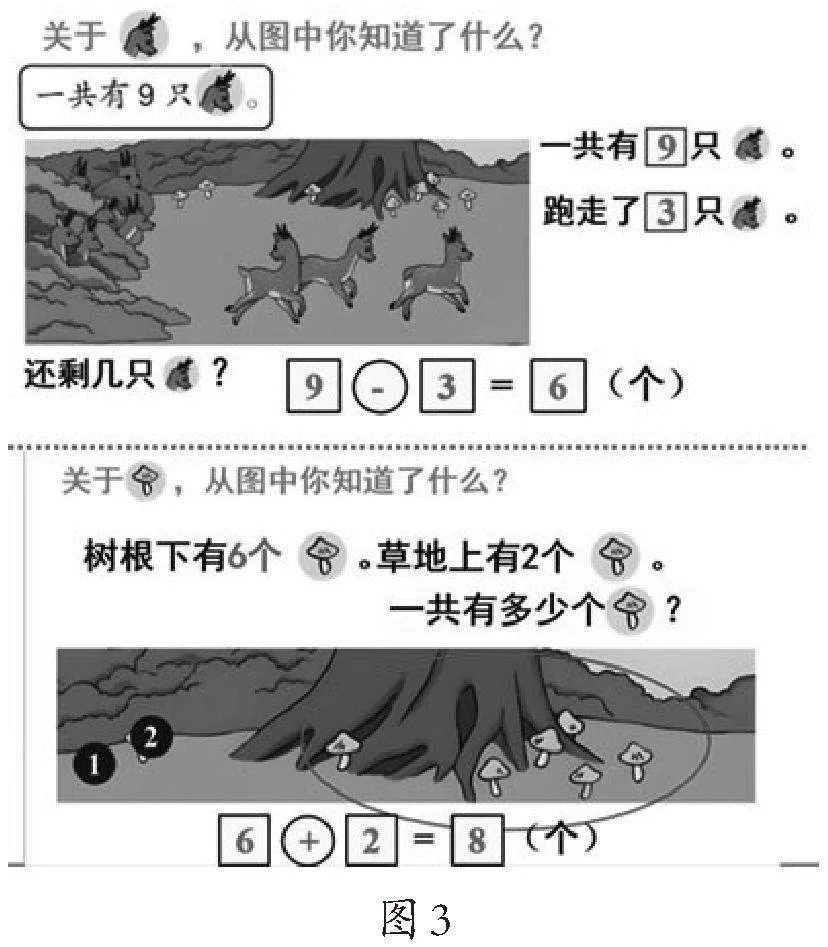
（课件出示小鹿图和蘑菇图两道题的解题过程。如图3）

师：比较一下我们刚刚解答的这两个问题，有什么不一样的地方？

生：这个算式中是9，第二个算式中是8。

生：第一个算式是用减法，第二个算式是用加法。

师：为什么第一个问题要用减法，而第二个问题却用加法呢？

生：因为第一个问题中是跑走，第二个问题中没有跑走。

师：所以，第一个问题中是从整体中去掉一个部分，而第二个问题中是把两个部分合起来。

问题分析

从以上片段可以看出，教师没有孤立地教学今天的解决问题，而是引导学生结合之前学过的大括号加工信息，将前后知识建立有机的联系，并通过数量关系解释选择加法或减法的原因，但很明显整个教学过程并不顺畅。是什么原因呢？

一、信息呈现不当，误导学生思维

教学时呈现的“小鹿图”中，藏在树丛中的小鹿只数实际上是本题想要学生解决的问题，而非已知条件。但图中6只小鹿都露出了半个脑袋，学生是可以直接通过数一数的方法解决问题的。在学生看来，通过收集信息、分析数量关系去解决问题，显得多此一举。一旦学生根据图示将6只小鹿作为已知条件数出来之后，就完全偏离了教学的目标。

二、素材过于抽象，学生难以理解

在分析数量关系时，笔者尝试借助前期学生接触过的大括号，希望通过将新知转化为旧知的方式，来帮助学生建立整体与部分之间的关系。但对学生来说，大括号本身就过于抽象，加之需要梳理的信息用文字的形式呈现，大大提高了学生理解的难度。因此，在这个环节的处理上，学生几乎是无法接受的。不仅没有落实教学任务，反而给学生带来负面的影响。

三、对比流于形式，教师和盘托出

从学生的回答中不难发现，一年级的孩子在分析异同时会更加关注直观数据的异同，如果不做适当的引导，比较难关注到解题方法的区别。如此一来，影响教学效率不说，还容易让学生抓不住问题的重点。此外，学生不能用规范的语言去描述用加法或减法的理由。在教学中，教师强行灌输整体与部分的概念，却没有解释两个概念真正的含义。对于学生理解数量关系，建立整体与部分的数学模型毫无帮助。

教学重构

基于以上反思，笔者进行了重构。

一、弱化直观图片，强调文字信息

（将主题图进行处理，将草堆里的小鹿、天鹅几乎全部遮挡）

师：从图中你知道了哪些信息？

生：有3只小鹿跑了出来。

师：你是怎么知道的？

生：我是数出来的，1、2、3。

师：哦，他是用数一数的方法，知道跑出来了3只小鹿。你还知道了什么。

生：图片的上面有个数字9。

师：图片上面的这句话你解读出来了吗？读一读。

生：一共有9只鹿。

师：这句话是什么意思？

生：表示这里一共有9只鹿。

师：这9只，也是数出来的吗？

生：不是的，是题目直接告诉我的。

师：原来看文字也可以知道数学信息，真了不起。

思考：将主题图中探出脑袋的小鹿进行处理后，学生本能地就不会去数草丛里有几只鹿，转而去发现与众不同的信息。同时，教师有意引导学生区别两个信息的获取方式，渗透了“不用数，看文字也能获取数学信息”，为后续学生学习更大的数，解决更复杂的问题提供了技术的引导。

二、借助直观图形，理解抽象概念

（学生获取信息并提出问题后，教师在黑板上画出连续的9个格子）

师：我用格子表示小鹿，看我画了几个格子？

生：9个。

师：现在我用一个大括号把它们都括起来，你知道表示什么意思吗？

生：一共有9只鹿。

（学生边说，老师边把“一共有9只鹿”的板贴取下，贴在大括号下面的位置）

师：原来这个大括号表示“一共有9只鹿”。“跑走了3只”，在图上怎么表示呢？

（学生上台板演，把右边的3个格子画掉）

师：直接从图中的9个格子里画掉3个，为什么？

生：因为跑走的3只就是从9只里面跑走的。

师：什么意思，谁听懂了？

生：是从这9只里面跑走了3只。

师：也就是说，这3只是9只里的一部分。

（教师边说边把“跑走了3只”板贴在3个格子上面）

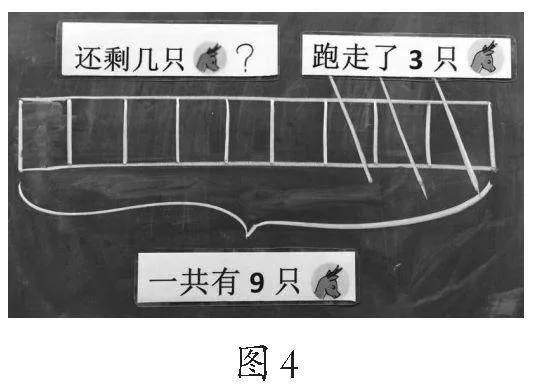
师：那这个问题该贴在哪儿呢？

（学生上台演示，如图4）

师：为什么贴在这里？

生：一共有9个格子表示有9只鹿，跑走了3只，也就是这3个格子，那剩下来的格子就表示剩下几只鹿。

师：谁听明白了？

（教师请3个学生复述一下他的意思）

师：在这里，我们说“一共有9只鹿”表示一个整体，“跑走的3只”是9只中的一部分，剩下的6只小鹿也是9只中的一部分。

（教师边说边把3个格子涂红，把剩下的6个格子涂黄，并板书“整体”“部分”）

师：看着图，你能说说“整体”是什么意思吗？

生：“整体”就是全部的鹿。

生：“整体”就是完整的、全部的。

师：“部分”表示什么意思？

生：“部分”就是一部分。

生：“部分”就是左边的和右边的。

师：如果把我们全班同学看作一个整体，第一大组的同学就是整体中的一部分，那么剩下来的部分在哪里？举手给我看看。

（第二、三、四大组的学生纷纷举手）

师：我们发现，从整体里去掉一部分，就是剩下的部分。

思考：与第一次教学相比，这次笔者借助更加具体的格子图，来帮助学生建立整体与部分之间的关系。同时格子图的渗透也为学生后续学习条形图、线段图做好铺垫。有了格子图的帮助，学生能够自然地将信息、问题匹配到图片中，并在师生的对话中进一步理解“整体”与“部分”的概念。教师借助学生熟悉的生活情境加深他们对“整体”与“部分”的理解，同时引出数量关系。虽然这里的数量关系是由教师陈述的，但从学生举手的情况来看，他们已经初步理解了“部分”与“剩下的部分”的概念。

三、对比分析异同，助力模型建构

（出示小鹿图和天鹅图，并将算式中的减号标红）

师：在解决这两个问题时有什么相同的地方？

生：都是用减法。

师：为什么都是用减法？

生：都是求剩下的部分。

生：都是从一共里面去掉的。

师：用数学的语言说，也就是从整体中去掉一部分，求剩下的部分。

（继续出示蘑菇图，并将算式中的加号标红）

师：解决这个问题时又有什么不一样呢？

生：用加法了。

生：我们要算的是合起来一共有多少蘑菇。

生：我们要算的是整体。

师：真了不起，他能马上用上今天刚学的词——整体。那我们知道的“树根处有6朵蘑菇”，在数学上称为——

生：部分。

师：还有一部分在哪里？

生：在草地上。

思考：周玉仁教授曾说过，新教材认为学生了解了生活情境，就自然而然地会列式解题，不需要去解析其中的数量关系，这样，一旦遇到两步计算问题，学生就束手无策了。在之前的教学中，笔者并没有意识到建立数量关系的重要性，甚至有意去回避“整体”与“部分”的渗透，担心对于一年级的学生来说太抽象。很明显，这样的做法是不明智的。

重构后的教学中，在小鹿图之后又安排了同类型的天鹅图作为巩固练习。通过小鹿图详细的教学过程，大部分学生都能够自主完成天鹅图完整的解题过程。在小结环节，先通过同类题的对比，让学生形成用减法解决问题的基本模型，再通过不同类型题的对比，让学生区分用加法解决问题的基本模型。从学生的回答中欣喜地发现，他们已经能够将前面环节渗透的“整体”与“部分”的概念自然地运用到说理中。

一年级的教学内容看似简单，实则非常考验教师的教学智慧。“解决问题”作为小学数学中的重点、难点，更需要引起一年级教师的重视。在低年级段教学生解决问题时，教师要立足学生的年龄特点和认知规律，借用几何直观来帮助学生建立数量关系，积累解决问题的基本活动经验，渗透数学的基本模型，为后续学习更复杂的问题打下扎实的基础。