凸显计数单位价值，感悟数概念的一致性

【课前思考】

在古埃及，将一切分数拆分为分子是1的分数（2/3是例外。古埃及人为何承认2/3至今仍是“千古之谜”），后人将分子是1的分数称为埃及分数（或单位分数、单分数）。例如，莱茵德（H.Rhind）纸草书首先用相当大的篇幅，用表格形式写出2/n型分数（分母为从5到101的奇数）分解成单位分数的结果（没有加号，从上下文可以看出加的含义）[1]，例如，2/29=1/24+1/58+1/174+1/232。利用这张表，可把7/29这样的分数表达成单位分数之和，例如，7/29=1/6+1/24+1/58+1/87+1/232。古埃及人利用单位分数就可以对分数进行四则计算，但如此之繁复导致他们未能把算术和代数发展到高水平[2]。看似繁杂、笨拙的分解方法却吸引了很多数学家进一步探究，例如，斐波那契运用贪心法（每次平均分得到最大分数，贪心法也是现代计算机科学中的一种算法）能将任意一个分数拆分为埃及分数但没有证明，直到1880年英国数学家西尔维斯特首次严格证明了贪心法的正确性。

在数学教学中也有很多老师从“如何将某些特殊分数分解为埃及分数之和”的角度设计了有趣的学习活动，初步培养学生的计算思维或探究发现能力[3-4]。事实上，如何将一个分数分解为埃及分数对很多学生来说都有难度：一方面直接分解就有困难，另一方面有的分数有不同的分解方法，再探究发现其规律更难。例如，笔者花了半天时间试图根据2/29的埃及分解式推导出7/29的如上分解式，但未能成功，但笔者利用贪心法，很容易就找到7/29=1/5+1/29+1/145。除此之外，埃及分数还有哪些现代育人价值呢？如何用好贪心法呢？

进一步查阅资料以及学习2022年版课标，我们找到了答案——利用埃及分数凸显分数单位的价值。2022年版课标的一大特点是强调数学课程的整体性与发展性。整体性主要表现为“一致性、结构性”，例如，强调“数与运算的一致性”，其核心是计数单位。利用埃及分数感悟分数单位的价值有助于落实“把握数概念的一致性”这一目标，计数单位是理解数的意义、提高运算能力的根本。

再进一步思考可知，这种不同体现在两种不同分物过程中：一曰现代分法，二曰古埃及分法。例如，将3个面包平均分给4个人，现代分法是“将1个面包平均分4份，每人获得1/4个；重复2次，每人获得3个1/4，也就是3/4个面包”（当然，“更现代”的分法是将3个面包作为整体“1”）。古埃及人的分物思路有其“更现实”的一面：每次分到“最大块”；将剩余的继续分，但每次仍得到最大块；如此继续下去。显然，古埃及人每次得到的是最大的分数（单位）。因此，虽然“单位分数”与“分数单位”的形式相同但功能不同：埃及分数虽然也具有“计量单位”的价值，但只计量一次；而后者可以“计数、计量”多次，从而能产生所有的分数。

认识到这两种分法都能在直观分物的活动中认识分数单位、感知分数单位的相对大小；初步感悟任何一个分数都可以由“分数单位累加”而成：既可以是同一个分数单位的多次累加，也可以是不同分数单位的累加；所有的分数单位可以像自然数一样“排出大小顺序”、也蕴含着规律。因此，我们决定在四年级或五年级学生学习分数的意义之前增加一节分数的拓展活动课。在“分饼活动”中让学生经历两种不同方法，积累活动经验；通过古今方法对比更有助于学生感知分数单位的大小，感悟分数的意义，发展数感。

基于以上思考，我们将本节课的学习目标设定为：

1.通过分饼活动，感悟分数产生的必要性，认识并理解埃及分数的意义，通过分数墙，沟通分数与整数之间的联系，体会数概念的一致性。

2.在分物的过程中，积累分物的经验，体会分物时分数单位越大越方便，感悟埃及分数的现实价值，直观感悟单位分数的大小及排列规律，培养数感。

3.感受古埃及人的智慧及数学文化的价值，激发学生的数学学习兴趣与探究欲望。

【教学过程】

一、第一次“分饼活动”中了解埃及分数的含义

1.问题激趣，尝试解决问题。

创设吃早餐时遇到问题的情境，教师问：你们愿意帮助我吗？请看下面的任务及活动要求。

任务一：将3张同样大的饼平均分给4人，每人得到多少张饼？

活动要求：用你喜欢的方式将分的过程简洁地记录在学习单上。分的时候可以折一折、剪一剪、画一画、写一写。

学生独立完成后小组交流，而后进行全班分享。

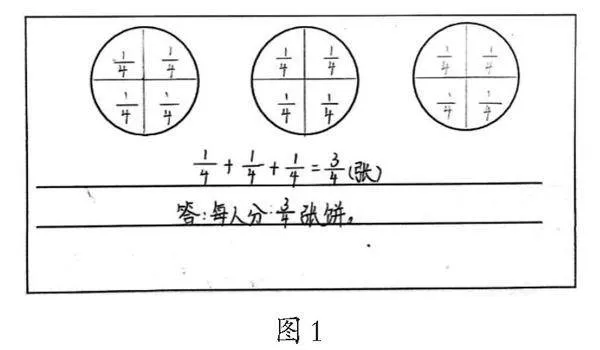
生1：我把每张饼平均分成4份，每份就是1/4张，每人取每张饼的1/4，分到了3份，就是3个1/4张饼。（如图1）

教师追问：把1张饼平均分成4份，1份是几张呢？（在示意图中涂色1份）没错，1份就是1/4张饼，1个1/4张。2个1/4张，3个1/4张，一共是几个1/4张？

学生习惯性地将分数表述为“这张饼的1/4”，教师在黑板左边适时板书“3个1/4=3/4”，强调可以用分数表述“数量”：四分之几张饼。

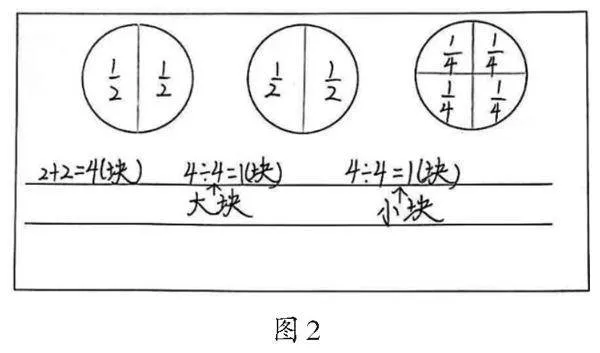
生2：我想先把其中的2张饼，每张饼平均分成2份，一共有4份，每人可以分得1/2张；再将剩下的1张饼平均分成4份，每人又可以分得1/4张。两次刚好分完，每人分得的饼是（1/2+1/4）张。（如图2）

在前面板书“3个1/4=3/4”的后面，教师继续板书：1/2+1/4。

2.对比理解，初步感悟两种分法的不同。

教师追问：两种分法，每人分到的饼有什么特点？

生：第一种分法，每人得到3小块；第二种分法，每人得到1大块1小块，是半张再加半张的一半。

师：这两种分法得到的结果一样大吗？可以怎么验证？（学生移动贴在黑板上的“饼图”）你真有办法，借助模型通过验证发现：3/4张饼等于1/2张饼加1/4张饼。如果倒过来，那（1/2+1/4）张饼是不是也等于3/4张？

教师引导学生说出两种分法各自的优势。

3.追本溯源，揭示埃及分数。

师：这两种分法，你更喜欢哪一种？

生：我更喜欢第一种，因为这种分法我比较容易想到，分给几个人，就将每张饼分成几小块。

生：我更喜欢第二种，因为分到的饼的块数比较整。

师：第二种分法分饼的结果有什么特点呢？

生：分到的饼中有更大的一块。

师：这种分法就是古埃及人最早的分物方法，他们的想法很朴素，就是想每次分到的饼都尽可能大。

师：我们一起再说一说埃及分法的过程。（课件操作演示埃及分法）有人也把这种分法称为贪心法，谁知道贪心在哪儿呢？

生：因为每次他都想分得最大。

师：贪心法出自莱茵德纸草书，书中详细记载了分数最初的样子。我们一起看看，你们能看懂这些符号是什么意思吗？（课件呈现莱茵德纸草书图片、古埃及表示分数的象形文字，图略）

生：他们是用竖线表示数，有几条竖线就表示是几。

生：我觉得它们的分子是一样的，因为它们上面都是椭圆形的。

师：正像你们所说的，古埃及人用一个椭圆形符号表示这个数是分数，在这个椭圆形符号下画几条竖线，就表示分母是几，比如这个数就表示1/2，这个就是1/3，1/4，1/8……（图略）

师：观察这些埃及分数，你们有什么发现？

生：古埃及人发明的分数，分子都是1。

师：你们知道为什么埃及分数分子都是1吗？

生：因为每次他们都是平均分。

生：因为每次他们都分到1份。

师：老师特意查阅了分数的发展史，史书上是这样说的：古埃及人在平均分猎物的时候，总是先保证每人分到1份，而且要尽可能大，这样比较公平。如果有剩余，再一轮一轮地分下去，直到分完为止，所以他们发明的分数，分子都是1。像这样分子是1的分数，就叫埃及分数。（板书题目：埃及分数）你们觉得这两个埃及分数1/2和1/4谁更大啊？

生：1/2更大，因为它是半张，1/4是半张的一半。

[评析]以“分饼”作为情境，为分数的引入提供最基础也是最重要的现实背景，激发学生的探究欲望，主动参与探究任务。通过语言表征、算式表征、图形表征解决实际问题，理解分数的“量”的含义，初步感悟分数是一个数，加深学生对于埃及分法及埃及分数的理解，同时沟通两种分法之间的联系，初步感悟分数单位。

二、巩固“贪心法”，体验“分数由不同单位分数累加得到”

1.增加饼和人的数量：5张饼平均分给6人。

教师课件出示任务二：尝试用贪心法将5张同样大的饼平均分给6人，每人分到多少张？

马上有学生回答：因为要分给6人，所以我想把每张饼都平均分成6份，每份就是1/16张，每人取每张饼中的1/16张，分到了5份，就是5/6张。

教师板书并让其他学生再说一下。

师追问：古埃及人会怎么分呢？带着刚刚的经验，用贪心法分一分。

学生独立思考并简单画示意图后，先小组交流，再全班交流。

教师收集三幅典型作品并同时呈现在黑板上。学生先独立读懂这些作品，并做比较，然后交流汇报。

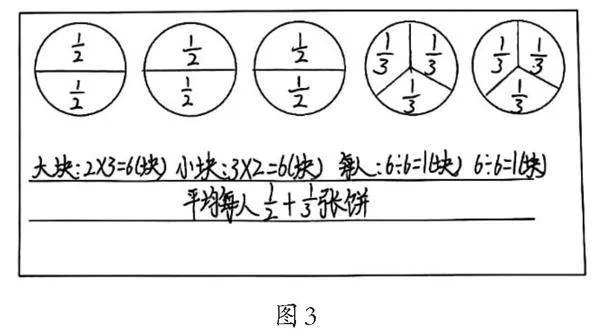
生1：我读懂了第一幅作品（如图3），先分3张饼，将每张饼平均分成2份，一共有6份，每人可以分到1/2张；再将剩下的2张饼都平均分成3份，每人又可以分到1/3张。两次刚好分完，每人分得的饼是（1/2+1/3）张。

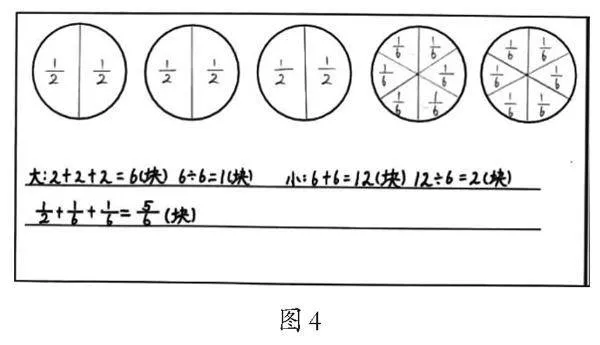
生2：第二幅作品（如图4）是先分3张饼，将每张饼平均分成2份，一共有6份，每人可以分到1/2张；再将剩下的2张饼每张平均分成6份，每人又可以分到2个1/16张。两次刚好分完，每人分得的饼是（1/2+1/16+1/16）张。

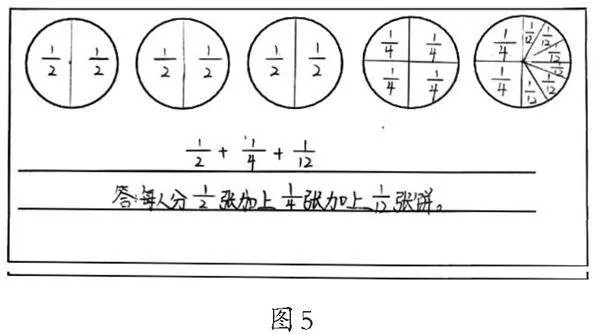
生3：第三幅作品（如图5），先分3张饼，将每张饼平均分成2份，一共有6份，每人可以分到1/2张；再将剩下的2张饼平均分成4份，每人又可以分到1/4张。还剩下半张，再将剩下的半张饼平均分成6份，这时候每人分到的是1/12张。三次分完，每人分得的饼是（1/2+1/4+1/12）张。

教师引导学生在互评的过程中，总结贪心法的原则，发现图5虽然能够解决问题，但是不够贪心。学生借助“饼模型”直观验证不同分法得到的饼的大小相等。

2.继续增加饼和人的数量：9张饼平均分给10人。

教师出示莱茵德纸草书中有关分饼问题：将9张同样大的饼平均分给10人，每人分到多少张？

学生很快想到用现代分法解决：把每张饼都平均分成10份……但马上有学生反对：每份快成“碎渣渣”了。

教师边用课件演示，边让学生说出古埃及人是如何操作的。

生：先把前面5张饼每张都平均分成2 份，每人分到1/2张，接着把后面4张饼每张平均分成3份，每人分到1/3张。

师：还剩下2/3张饼，平均分成10份，该怎么分呢？

生：可以借助图来思考，把2/3张饼，平均分成10份，就相当于把1/3张饼再平均分成5份，也就是把整张饼平均分成15份，所以每人又都分到了1份，也就是1/15张饼。

师：谁能用一个算式把分的过程说一说？到底是多少张呢？（板书：1/2+1/3+1/15）

师：你们知道吗？在莱茵德纸草书中，古埃及人真正的分法是这样的：每人分到了（2/3+1/5+1/30）张饼，这个2/3是唯一一个分子不是1的埃及分数。但为什么这么分，至今仍是个未解之谜，等待着同学们去探究。

3.对比感悟，感受“分数由单位分数累加得到”。

教师再次引导学生对比两种方法，启发学生辩证地看待现代分法与埃及分法。

师：和现代分法相比，你们觉得埃及分法怎么样？

生：我觉得埃及分法分到的饼比较大，但有点麻烦，必须动手实际操作才能得到结果。而现代分法得到的饼太小，都成碎渣了，还不方便数。

生：我喜欢现代分法，因为我比较容易想到，一下子就能得到结果。

教师总结：现代分法只产生一个单位分数，数几次分子就是几；埃及分法产生了几个单位分数，这几个单位分数合起来就是现代分数。看来单位分数太重要了。

[评析]通过增加饼和人的数量，继续研究分饼问题，借助前面的学习经验，尝试用贪心法分饼。在分物的过程中，积累分物的经验，通过多次对比分饼的不同方法，辩证地看待两种分法的优劣，体会分物时单位分数越大越方便，感受古人智慧，感悟埃及分数的现实价值，同时体会现代分法的优势。不管哪种分法，单位分数都起到重要作用。

三、借助分数墙，理解分数单位的意义，体会数概念的一致性

1.发现规律，理解分数单位。

教师引导学生观察黑板上的等式，发现规律。

3/4=1/2+1/4 5/6=1/2+1/3

5/6=1/2+1/4+1/12 9/10=1/2+1/3+1/15

学生能够发现等式中都有1/2，分数可以表示成埃及分数相加的和且存在从大到小排列的规律。

师：你们怎么知道这些埃及分数是由大到小排列的呢？

生：因为分饼的时候，每次分的尽可能大，所以后一次总比前一次小。

师：在这些埃及分数中，谁是最大的埃及分数？第二大的埃及分数呢？然后呢？

生：1/2，1/3……

2.沟通联系，深化理解。

师：单位分数的大小真是这样的吗？

教师动态呈现出分数墙：先出示第一行，再出示第二行，最终结果如图6所示，并引导学生想象可以继续“细分”下去，“没完没了”，学生再次感悟单位分数的大小，没有最小的单位分数。

同时，教师引入我国古人对特殊分数的命名：1/2叫“半”，1/3叫“少半”，1/4叫“弱半”，通过名字，就能形象地知道谁大谁小。学生初步感受到无论古埃及人还是中国古人都从各自角度认识并使用分数，感受古代劳动人民的智慧。

教师再选1/4，学生向右继续数：2/4，3/4，4/4，借助想象仍然可以继续数下去。学生说：分数也可以数出来！

3.回顾反思，提升思维。

师：没错，这和我们数整数是一样的，我们在数物体个数的时候，谁是最小的计数单位？

生：1是最小的计数单位。

师：比1大的计数单位有哪些啊？

生：十、百、千、万……

师：如果我们把这些埃及分数在数线上表示出来，它们的位置在哪里呢？1/2，1/3，1/4……

教师通过课件直观地将前面的“分数墙”压缩为“数轴”，通过数轴再次感受分数单位的大小。

师：通过今天的学习，你对埃及分数有了什么了解？

生：我觉得古埃及人非常聪明，能够发明埃及分数。

生：我觉得埃及分数写起来比较麻烦，用一个分数表示比较简便。

生：我觉得埃及分法很有用，可以用它表示其他分数。

教师从辩证的角度总结埃及分数，强调埃及分数的出现在人类历史上是一项了不起的成就，里面蕴含很多有价值的数学问题，引发学生更深层次的思考与探究。

[评析]引领学生搭建分数墙，借助分数墙验证埃及分数的大小，直观感悟单位分数的大小及排列规律，再由分数墙抽象出数轴，借助几何直观，进一步感受分数单位的大小，沟通分数单位和整数计数单位之间的联系，体悟数的概念的一致性，发展学生的数感。

参考文献：

[1]梁宗巨.世界数学通史（上册）[M].沈阳：辽宁教育出版社，2005：155.

[2]莫里斯·克莱因.古今数学思想（第一册）[M].上海：上海科学技术出版社，2002：19.

[3]陈六一.“埃及分数”教学设计[J].中小学数学，2018（7/8）：59-61.

[4]王珍，章勤琼.巧借数学文化，渗透计算思维[J].小学教学（数学版），2023（3）.

（作者单位：北京教育学院数学与科学教育学院，北京市石景山区爱乐实验小学）