重推理，有条理地讲道理

学生学习了2、5的倍数特征之后，虽然记住了知识结论并能熟练地进行判断，但仍然不能解释为什么只要看个位就可以了。学习了3的倍数特征之后更是疑惑为什么判断方法与判断2、5的倍数的方法“完全不同”。如果只是记住了事实，即使形成了熟练的操作程序，这样学习的知识也往往是不扎实的，只有互相关联且建立在概念和原理基础上的知识，才能够比较容易地被用于新的情境[1]。

教学2、5的倍数特征时，如果能充分地展开知识的发生和发展过程，以根据概念推理和计算实验获得的经验事实作为推理的出发点，引导学生有条理地讲道理，给合情推理形成的猜想打上演绎推理的补丁，不仅可以使获得结论的过程更加严谨，使数学结论更加可靠，而且能培养学生重论据、有逻辑的思维品质，发展科学态度与理性精神。

关于推理与证明，《美国学校数学教育的原则和标准》指出：3～5年级，学生应在数学推理方面进行重要的思维转变，认识到推理和证明是数学的基础。学生应该认识到只通过几个例子说明猜想正确是不够的，并认识到可以用反例来反驳一个猜想。他们应该学习通过考虑一系列例子，能够对一般性质以及他们发现的联系进行推理。

一、积累基本的经验事实

在小学，除了学习整数的运算，还要研究整数的性质。探索2、5的倍数的特征同时联系了这两个方面。从学习带余除法这一初等概念开始，学生将从一个完全不同的角度来考察自然数：它们不再只是计算的工具，而是一个具有内在意义的对象[2]。

整除是整数理论的核心，是研究整数性质的基石。对于整数a和整数b，如果存在一个整数k，使得a=b×k，那么就说a能被b整除，记作b|a。它的含义是a恰好能被b除尽，且商是整数[3]。整除的一个引理（也称整除性质定理）是：设A、B、C是整数并满足A=B+C，假设一个不等于0的整数x整除A、B、C中的两个数，那么x必定同时整除第三个数[2]。

虽然小学生并不直接学习整除性质定理，但是基于一些基本概念和运算推理，容易归纳得到一些相关的经验事实。例如，因为10=2×5，2=2×1，10与2都是2的倍数，所以20（10×2）与12（10+2）也是2的倍数。这个结论可以通过计算实验得到验证。其中，12是2的倍数推理的依据是：一个数的倍数的和与差，仍为该数的倍数。这个定理的证明过程略。

以上述基本的经验事实为出发点，可以归纳得到22（rUMJrLIL1r+YOsX+hfu0SNzwMxzWWeUzXh1EY2lGaOU=10×2+2）、32（15×2+2）、42（20×2+2）等个位上是2的数都是2的倍数。进一步，通过类比推理得到：个位上是2的倍数的数就是2的倍数。

逻辑推理是得到数学结论、构建数学体系的重要方式，是数学严谨性的基本保证，是人们在数学活动中进行交流的基本思维品质。但是，在强调推理证明的同时，也不能忽视计算实验。以下教学案例，通过计算实验与推理证明相结合的方式获得基本经验事实，并以此作为进一步推理与证明的出发点，通过归纳推理与类比推理获得数学结论，在学习数学知识的同时积累起研究数学问题的活动经验。

1.提问。

师：上节课我们学习了因数、倍数，今天学习2、5的倍数的特征。看了这个课题，有什么问题想问的？

生：为什么要研究2、5的倍数？

生：2、5的倍数有什么特征呢？

生：怎样才能一眼看出这个数是不是2、5的倍数？

生：它们有没有相同的倍数？

师：你们提出了很好的问题，其中最关键的问题是2、5的倍数有什么特征。我们先研究2的倍数有什么特征。可以怎么研究呢？从哪里起步？

生：我们可以找一些2的倍数来分析分析。

2.列举。

师：好，谁来找一些2的倍数？

生：2、4、6、8、10、12、…。

师：2的倍数有很多，你是怎么找到2的这些倍数的？

生：我是利用2的乘法口诀。

师：如果从中选择几个最简单的，你会选什么？

生：10、20，这些是整十数。

生：2、12、22，个位上都是2。

3.计算。

师：我们从最简单的开始。2是2的倍数，10是2的倍数，把这两个数加起来得到12，是2的倍数吗？

生：12除以2等于6，它是2的倍数。

生：可以把12分成10和2，10是2的倍数，2是2的倍数，12就是2的倍数。

师：用拆分的方法来解释，谁听懂了？

生：把12分成10和2，10里面有5个2，2里面有1个2，合起来12里面就有6个2，12是2的倍数。

生：10除以2是5，10是2的倍数，2除以2是1，2也是2的倍数，它们的和12就是2的倍数。

师：你们都解释得很好，现在如果在12的前面再加一个数字3，得到312，它是不是2的倍数？

生：最简单的方法，就是把312除以2，看看是不是整数，算出来商是156，是整数，所以312是2的倍数。

生：还可以把312进行拆分，分成300和12，300除以2等于150，12除以2等于6。这两个数除以2的结果都是整数，所以312是2的倍数。

师：40312还是2的倍数吗？你怎么想？

生：40312是2的倍数。我们可以把40312分成40000和312，用这两个数分别除以2，得出来都是整数，所以40312是2的倍数。

4.归类。

师：观察比较2、12、312、40312这些数，你有什么发现？

生：个位上都是2，它们都是2的倍数。

师：现在我们得到的结论是什么？个位上是2的数——

生：都是2的倍数。

通过列举、计算、归类等活动得到初步的猜想，这些活动都与具体的例子相联系。已经考察的例子分成两类：一类是作出推测之前的例子，由学生举出，它提示了推测；另一类是作出推测之后的例子，由教师设计，它印证了推测。一个猜想性的一般命题，假如在新的特例中得以证实，那么它就变得更可信了[4]。特别地，讨论2、12、312等这些有联系的例子，使得推理依据的是表征的结构，而不是随意和特例。

二、充分展开推理的过程

小学生学习数学，不可能完整地经历数学知识的产生和发展过程，也不太可能像数学家那样通过严格的证明来获得数学结论。但是，从他们已有的经验事实出发，经由一个命题到另一个命题的推理，既是他们获得数学知识与结论的途径，也是他们形成推理意识与证明能力的载体。

1.对比，归纳出初步的结论。

师：为什么个位上是2的数都是2的倍数呢？

生：我们以最大的40312为例。它可以拆成40000+300+10+2，40000、300、10都是2的倍数，2也是2的倍数，所以40312是2的倍数。

师：如果a代表0～9的数，下面哪些数是2的倍数？5a312、3a512、31a25、13a52、52a13。

生：5a312、3a512、13a52都是2的倍数，31a25、52a13不是2的倍数。

师：你是怎么想的？

生：我们以5a312为例。它可以拆成50000+a×1000+300+10+2，前面的整十数、整百数、整千数、整万数等都是2的倍数，2也是2的倍数，所以5a312是2的倍数。

师：52a13不是2的倍数，又怎么解释？

生：一样的道理，52a13可以拆成50000+2000+a×100+10+3，前面的加数都是2的倍数，关键是看最后的加数3，3不是2的倍数，所以52a13不是2的倍数。

师：综合他们两人的想法，我们可以怎么判断一个数是不是2的倍数？

生：看个位就可以了。

2.类化，概括出最终的结论。

师：5312a是2的倍数吗？

生：不一定，如果a代表的数是7，它就不是2的倍数；如果a代表的数是8，它就是2的倍数。

生：如果a是2的倍数，5312a就是2的倍数；如果a不是2的倍数，5312a就不是2的倍数。

生：我觉得一个数是2的倍数和不是2的倍数可能性是一样大的，都有5种情况。

师：这是什么意思，谁听懂了？

生：他的意思是说，如果a代表2、4、6、8、0，它就是2的倍数；如果a代表1、3、5、7、9，它就不是2的倍数。

师：现在知道2的倍数长什么样吗？有什么特征？

生：个位上是2、4、6、8、0的数是2的倍数。

生：个位上是2的倍数的数是2的倍数。

生：个位上是偶数的数是2的倍数。

3.说理，有条理地讲道理。

师：为什么判断一个数是不是2的倍数，只看个位就可以了？这个道理你能讲清楚吗？同桌一人讲一人听，讲的人要讲得有条理，听的人要听出有没有道理。

生：任何一个多位数，都可以拆分成整万、整千、整百、整十的数再加个位数，前面整万、整千、整百、整十的数一定是2的倍数，所以如果个位上的数是2的倍数，那么这个数就是2的倍数，如果个位上的数不是2的倍数，那么这个数就不是2的倍数。

生：不用那么复杂。任何一个多位数，都可以拆成前面的数乘10再加上个位上的数，一个数乘10后末位上是0，肯定是2的倍数，再看个位上是不是2的倍数就可以了。

师：这两种解释有什么相同与不同？

生：拆分的方法不一样，但思路是相同的，都是把一个多位数拆分成10的倍数加上个位数。10的倍数肯定是2的倍数，所以只要看个位上的数就知道它是不是2的倍数了。

在这个构造一般结论的过程中，学生懂得了通过简单的归纳与类比，可以猜想或发现一些初步的结论，知道从一些事实和命题出发，依据规则可以推出其他命题，初步感悟逻辑推理过程及其发现知识的意义。特别地，当他们经常有机会通过各种模式去确认一个一般结论时，推理就会成为他们判断一个结论正确与否的标准，而不是依赖权威的判断或者特殊的检验[5]。

三、形成灵活的迁移应用

在数学上，人们通过推理形成各种命题、定理和运算法则，促进了数学的发展。在学习中，学生积累了发现或得到一个数学结论的基本活动经验，既要依赖于对例子的考察，也要依赖于有逻辑的推理。通过推理获得知识的价值是显而易见的，可以发展学生的思维，帮助学生养成讲道理、有条理的思维习惯，形成实事求是的科学态度与敢于质疑的理性精神。

任何一个多位数都可以写成a×10+n的形式（a、n都是整数），其中n表示个位上的数。因为10=2×5，所以a×10既是2的倍数也是5的倍数。因此，2的倍数特征与5的倍数特征是相似的，解释说理的方法也是同构的。基于2的倍数特征的探索，5的倍数特征也就“不证自明”了。

1.类比迁移。

师：我们已经知道了2的倍数的特征，回想一下，我们经历了怎样的过程？是怎么得到数学结论的？同桌讨论一下。

生：先举了一些例子，然后猜测，接着我们进行验证，利用直接除或分解法，最后得出结论：个位上是0、2、4、6、8的数是2的倍数，你们同意吗？

（教师板书：“观察例子，形成猜想，计算验证，概括结论”）

师：5的倍数有什么样的特征呢？请在小组内讨论，完成探究学习单。我举的例子（ ），我们的猜想（ ），计算与验证（ ），我们的结论（ ）。

师：哪个小组上来交流一下？

生：个位上是2的数是2的倍数，我们猜想个位上是5的数是5的倍数。举的例子是35，一种思路是35除以5等于7，商是整数，说明35是5的倍数；另一种思路是把35拆成30加5，5是5的倍数，30也是5的倍数，所以35是5的倍数。我们的结论是个位上是5的数是5的倍数。

生：我们组的猜想是个位上是0或5的数是5的倍数。举的一个例子是720，验证的方法是把720分成700和20，700是5的倍数，20也是5的倍数，因此，720是5的倍数。还有一种验证的方法是720除以5是144，也可以证明720是5的倍数。另一个例子是685……我们得出的结论是个位上是0或5的数都是5的倍数。

师：听懂他的解释了吗？有没有疑问或补充？

生：我们也可以说个位上的数是5的倍数，这个数就是5的倍数。

生：2的倍数与5的倍数，解释的方法是一样的。前面的数都是整万、整千、整百、整十的数，它们都是2、5的倍数。关键是看个位，个位上的数是2的倍数，那么它就是2的倍数，个位上的数是5的倍数，那么它就是5的倍数。

2.联系沟通。

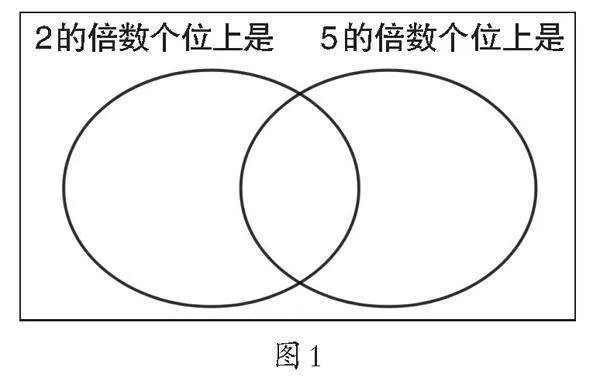
师：我们把学到的知识整理一下，填到下面的圈里。（如图1）

师：两个圈共同的部分应该填什么？

生：填0。

师：表示什么意思？

生：个位上是0的数，既是2的倍数，也是5的倍数。

师：为什么？

生：因为个位上是2、4、6、8、0的数是2的倍数，个位上是5、0的数是5的倍数，它们都有0。

生：个位上是0的数，它可以写成一个数乘10的形式，10等于2乘5，这个数一定有因数2和5，所以它既是2的倍数，也是5的倍数。

师：先用1、2、5、a四个数字组成四位数，再判断它是不是2的倍数，是不是5的倍数。

师：如果是2的倍数，个位上是几？如果是5的倍数呢？

生：2的倍数个位上是2，如15a2、1a52、51a2……5的倍数，个位上是5……

师：如果个位上是a呢？

生：当a代表2、4、6、8的时候是2的倍数；当a代表5的时候是5的倍数；当a代表0的时候，它既是2的倍数也是5的倍数；当a代表1、3、7、9的时候，既不是2的倍数也不是5的倍数。

师：当一个问题中有不确定的因素时，要分类讨论可能出现的情况，用这种方法可以把问题想得更全面，在中学的数学学习里经常用到这样的方法。

从教学知识的分类来看，2、5的倍数特征属于命题教学的范畴。数学命题的教学要注重过程，包括命题产生过程和推理证明过程。无论推理还是证明，都需要使用正确的命题、合理的推理形式和适当的表达形式。在这里，虽然推理的出发点是学生的经验事实，而不是严格的数学定理，但推理的方法和结论都是正确的，表达的形式也是他们可以理解的。

根据数的意义，把多位数写成各个数位上的数乘10n的和的形式，“数字”就成了“所有量”的占位符，学生可以通过“数字”来说明对象的数量结构，而不必具体展示这个对象。这种基于表征的推理证明，是小学阶段构造一般结论的有效途径，而且这样做可以为以后的证明思维提供基础[5]。如3750=3×1000+7×100+5×10+0×1，由于100=4×25，在这个展开式中整千、整百数一定是4和25的倍数，因此，判断一个数是不是4或25的倍数，只要看展开式中的整十数与一位数即可，即看一个多位数后两位是不是4或25的倍数。不仅如此，如果改写以上的展开式，表示为3750=（3×999+3）+（7×99+7）+（5×9+5）+（0×9+0），每个括号内的乘加算式中，乘法项都是3的倍数，因此判断3750是不是3的倍数，只要看加法项的和（即各个数位上数字之和）是不是3的倍数即可。2、3、4、5、25的倍数特征是共通的！数学的优美在于，当有趣的结果出现时，通常是意想不到的，并且是基于合理的推理。数学深处的联系，既在意料之外，也在情理之中。

数学证明是一种表达特定推理过程的严谨的方法，对于数学家的工作及他们加深对数学的理解都是不可或缺的[6]。数学家推理的步骤是从前提出发，基于已经确定的定义、事实和原理，一步一步地到达结论[5]。

人们普遍认可证明应该在所有阶段学生的数学教育中发挥作用[6]。作为教育任务的数学，重要的不是像数学家那样严格地证明一个数学结论，而是经历由已知条件出发，通过正确的推理方式得到一个数学结论的过程。小学阶段的证明，并不等于数学家眼中的证明，而是一种广义的，由一系列“可以接受”的论据组成的，旨在得到共同体认可的构造过程[5]。重推理，有条理地讲道理，是促进学生形成概念性理解，利用知识的逻辑体系探究数学命题的重要方式，也是阐释系统使用数学定义与公理的主要手段。

参考文献：

[1]全美数学教师理事会.美国学校数学教育的原则和标准[S].蔡金法，等译.北京：人民教育出版社，2004.

[2]伍鸿熙.数学家讲解小学数学[M].赵洁，林开亮，译.北京：北京大学出版社，2016.

[3]张奠宙，孔凡哲，黄建弘，等.小学数学研究[M].北京：高等教育出版社，2009.

[4]G.波利亚.数学与猜想：数学中的归纳和类比（第一卷）[M].李心灿，王日爽，李志尧，译.北京：科学出版社，2001.

[5]德斯皮娜·A.斯蒂利亚努，玛利亚·L.布兰顿，埃里克·J.克努特.证明的教学：从幼儿园到大学的视角[M].周超，鲍建生，译.上海：上海教育出版社，2015.

[6]蔡金法.数学教育研究手册（第二册）：数学内容和过程的教与学[M].北京：人民教育出版社，2020.

（作者单位：浙江省新思维教育科学研究院）