大单元整体教学视角下的小学数学教学

在当前核心素养导向的时代，帮助学生建立结构化知识体系、发展学生核心素养是教学的价值取向，基于单元又超越单元、实施大单元教学是实现教学价值取向的重要途径，改变单一课时教学视角、推进单元整体教学设计是实现教学价值取向的重要举措。那么，在当前小学数学教学过程中，如何贯彻落实2022年版课标的要求呢？下面，以“分数单位”一课为例进行阐述，期望为大单元整体教学的研究与实践提供参考。

“分数单位”是“数与运算”主题第三学段的教学内容。在这一主题教学内容中，数的认识是数的运算的基础，数的运算是数的认识的进一步发展，计数单位是数的认识与数的运算的联结枢纽，是理解算理的关键所在。因此，“分数单位”一课的教学，应该改变单一课时教学视角，通过大单元整体教学设计，沟通分数单位与分数运算之间的联系，促进学生建立数的认识与运算的结构化知识体系，发展运算能力和推理意识，形成和发展核心素养。

一、设计好教学的基准是大单元整体教学的重要基础

大单元整体教学强调知识的结构化，强调知识之间的内在联系，因此，学习新知的起点是知识结构化和系统化的重要基础。教学时，我们应该立足教学内容的知识基础，设计好教学的基准，为知识结构化和系统化奠定重要基础。比如，“分数单位”一课，分数单位本质上是分数的计数单位，分数单位决定了分数具有可数性，可数性是自然数、分数和小数的根本属性，这体现了数的本质的一致性，通过数一数计数单位，产生四则运算，这体现了数的认识与运算的整体性。因此，分数单位是分数四则运算的重要基础，教学的基准可以设计在自然数的计数单位上。

【教学片段】感悟计数单位，发现和提出问题。

师：老子在《道德经》中说“道生一，一生二，二生三，三生万物”，这句话告诉我们什么道理？

生：事物不断累积，就会越来越多。

师：在数学世界里，也是同样的道理。利用计数单位，数一数，数就会越变越大。

师：（事先在黑板上画好数线）在自然数的世界中，最小的数是几？（生：0）我们把0的家安顿在数线的起点处。

师：在自然数的世界里，最小的计数单位是——（生：一）我们把1的家安顿在0的后面（右边）。对了，这个计数单位一很了不起，有了它就会生出一个大家族，我们称它为自然数。下面，我们一起体验自然数大家族产生的过程。

师：1个一就是——（生：1）2个一就是——（生：2）3个一就是——（生：3）以此类推，10个一就是——（生：10）这时就产生了比一大的计数单位十，也就是10个一就是1个——（生：十）

师：我们用十作为计数单位接着数，1个十就是——（生：10）2个十就是——（生：20）3个十就是——（生：30）10个十就是——（生：100）这时又产生了比十大的计数单位百。比百还大的计数单位是——（生：千）比千还大的计数单位是——（生：万）接下来还有十万、百万等，这就是自然数家族的秘密。

师：（板书一、十、百、千、万等）从左到右计数单位越来越大，当我们有了计数单位的眼光后，就可以更加深刻地理解数的意义。比如，1234这个数是由什么组成的？

生：1个千、2个百、3个十和4个一。

师：真厉害，说明你们长大了，已经有了自然数计数单位的眼光。关于计数单位，你们能提出新的问题吗？

生：有没有比一更小的计数单位？

生：它们又会形成什么家族？

师：凭借你们的直觉，你觉得会是什么家族？（生：分数）今天我们就专门研究分数家族中的秘密。请你们在练习本上先任意写出几个自己熟悉的分数。

以上教学片段中，把分数单位的教学，设计在自然数计数单位的基础上，作为本节课教学的基准。通过老子《道德经》中的一句话，引出自然数的计数单位，从而使学生感悟计数单位的价值，体会自然数产生和形成的过程，学会用计数单位的眼光观察熟悉的自然数，理解自然数的意义，在此基础上，发现并提出新的问题“有没有比一更小的计数单位”，进行更为深刻的数学思考，为本课的学习奠定重要基础。

二、设计好教学的生长过程是大单元整体教学的根本保证

大单元整体教学强调知识的结构化，强调知识之间的内在联系，因此，知识的生长是知识结构化和系统化的根本保证。教学时，我们应该立足教学内容的数学本质，设计好教学的生长过程，让新知在生长中得以形成，让知识在生长中得以建构，从而促进知识的结构化和系统化，发展学生核心素养。比如，“分数单位”一课，分数单位本质上是自然数的计数单位一细分的结果，当把一平均分成2份时，就产生了新的分数单位1/2，2个1/2就是1个一；当把一平均分成3份时，就产生了新的分数单位1/3，3个1/3就是1个一；以此类推。因此，在自然数计数单位一的基础上，我们可以通过平均分，让知识得以生长，产生一系列比一小的计数单位，从而促进分数单位的形成与发展，促成知识的结构化和系统化。

【教学片段】产生分数单位，感悟内在联系。

1.体会1/2的产生及由其组成的4个一。

师：现在我们把1个圆平均分成2份，其中的1份用什么表示？

生：1/2。

师：（依次摆放）大家一起来数一数，看看今天我带来了几个1/2。

生：（齐声数）1个1/2，2个1/2，3个1/2，4个1/2，5个1/2，6个1/2，7个1/2，8个1/2。

师：（移动2个半圆卡片合成1个圆）你们发现了什么？

生：2个1/2组成1个一。

师：（移动8个半圆卡片合成4个圆）8个1/2组成几个一？（生：4个）很好，那么在数线上1/2的家在哪里？

生：（摆放对应的卡片）在0和1的中间。

2.体会1/4的产生及由其组成的2个一。

1/4的产生过程及由其组成2个一的过程与上面类似，此处省略。

师：在数线上1/4的家在哪里？

生：（摆放对应的卡片）在0和1/2的中间。

3.体会1/8的产生及由其组成的1个一。

1/8的产生过程及由其组成1个一的过程与上面类似，此处省略。

师：在数线上1/8的家在哪里？

生：（摆放对应的卡片）在0和1/4的中间。

4.形成分数单位的概念及家族。

师：（在一的左边板书1/2、1/4、1/8）像1/2、1/4、1/8这样分子是1的分数，我们称为分数单位。

师：凭借你的直觉，你觉得1/2和1/4之间还会有哪个分数单位？

生：（略加思考）1/3。

师：（补充板书1/3）1/4和1/8之间还有哪些分数单位？

生：（齐）1/5、1/6、1/7。

师：（补充板书1/5、1/6、1/7）还有没有比1/8更小的分数单位？

生：1/9、1/10、1/11……

师：（补充板书1/9、1/10、1/11……）它们越来越小，在数线上越来越靠近0，会住到0的家里去吗？

生：（信心十足地回答）不会！

师：这就是分数单位这个大家族的奥秘！

以上教学片段中，通过三次平均分，促进了知识的三次生长，逐步形成分数单位的概念，推进了教学的进程。通过数一数的方式，学生体会分数单位的可数性，感悟分数单位与自然数计数单位本质的一致性。利用数线，通过数形结合的方式，学生体会分数单位与自然数计数单位之间的关系，进一步发展数感。通过类比推理的方式，学生推断出其他的分数单位，明白自然数的计数单位一越分越细，产生的分数单位就越来越小，在数线上的位置就越来越靠近0，由此形成了分数单位的大家族。相反，自然数的计数单位越来越大，在数线上离0越来越远，由此形成自然数计数单位的大家族。这样设计，有利于学生感悟计数单位之间的关系，进一步发展数感，为理解运算的道理和形成核心素养奠定重要基础。

三、设计好教学的拓展是大单元整体教学的关键所在

大单元整体教学强调知识的结构化，强调知识之间的内在联系，因此，知识的拓展是知识结构化和系统化的根本保证。教学时，我们应该立足教学内容之间的内在联系，设计好教学的拓展，让新知在拓展中得以应用，让知识在拓展中得以关联，从而促进知识的结构化和系统化，发展学生核心素养。数的认识与运算是一个有机的整体，分数单位是分数四则运算的重要基础，是理解算理、掌握算法的关键所在。因此，对于“分数单位”一课，我们可以通过隐性的方式，将分数单位适当延伸到分数的简单四则运算中，让学生体会分数单位的作用和价值，感悟运算本质的一致性。

【教学片段】借助分数单位，感悟运算本质。

1.体会1/4在运算中的作用。

师：分数单位这个大家族还蕴含着深刻的秘密，下面我们一起来挑战几个数学问题，感受一下分数单位的无穷魅力。

教师在黑板上移动已有卡片，如图1所示。

师：请大家认真观察，这里左边有几个1/4？右边有几个1/4？

生：（异口同声）左边有2个，右边有1个。

师：你们真棒，已经拥有了分数单位的眼光。2个1/4是多少？

生：（轻易地回答）2/4。

师：回答正确，掌声鼓励。那么左边和右边合起来是几个1/4？

生：（轻易地回答）3个。

师：太棒了，你已经会数分数单位了。3个1/4是多少？

生：（异口同声）3/4。

师：看来这些问题太简单了。左边比右边多多少？（生：多1/4）右边比左边少多少？（生：少1/4）你们怎么可以这么厉害呢！把掌声送给自己。下面要来一个更难的问题，（手指着左边的2张卡片）2/4平均分成2份，1份是多少？

生：（异口同声）1/4。

师：这么难的问题你们都会，太了不起了！

2.体会1/8在运算中的作用。

师：下面换一种方式，我们请一位同学上来做小老师，在黑板上移一移，摆一摆，用1/8编几个问题来考考大家。

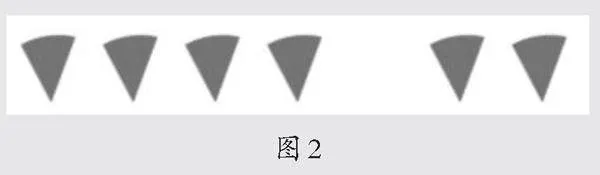
学生纷纷举手，一个学生上台移动已有图片，并摆出图2。

生（小老师）：左边和右边合起来是几个1/8？

生：（异口同声）6个。

生（小老师）：6个1/8是多少？

生：[68]。

师：这个小老师真厉害。我们再请一位小老师上来提出新的问题。

生（小老师）：左边比右边多几个1/8？

生：（异口同声）2个。

生（小老师）：2个1/8是多少？

生：2/8。

师：好棒。我们再请一位小老师上来提出更难的问题。

生（小老师）：4/8平均分成2份，1份是多少？

生：（抢答）2/8。

师：（笑着说）好玩吗？

生：（开心地说）好玩！

3.体会不同单位在运算中的作用。

师：在分数单位的世界里，更好玩的还在下面，如果你们还能说清楚，让别人听明白，我给你们一个大大的“赞”。

师：（在黑板上摆出图3）把它们合起来是多少？

学生犹豫，陷入沉思，少数人举手。

师：被难倒了吧！终于数不出来了。我们请这个举手的同学上来结合图片移一移、摆一摆，再说一说。我有个小小的要求，一定要说地球人说的话，要让别人能听得懂。

生：（边移动卡片边说）左、右两边分数单位不同，没办法数，因此，我们可以先把右边这张1/4的卡片替换成2张1/8的卡片，这样数一数就是3个1/8，合起来就是3/8。

师：如果大家听懂了，就给他热烈的掌声！

学生纷纷鼓掌。

师：太棒了！当分数单位不同时，不能直接数，这时我们需要把大的分数单位替换成小的分数单位，分数单位相同就能直接数出结果，这就是分数单位的奥秘！

师：还有信心继续挑战吗？

生：（大声喊）有！

师：（指着这两张卡片）1/4比1/8多多少？

生：（信心满满地在黑板上边操作边说）我们把这个1/4替换成2个1/8，2个1/8比1个1/8多1个1/8，也就是1/4比1/8多1/8。

师：又是一个厉害的地球人，如果你们同意他的说法，就给她掌声。

学生欣喜地鼓掌。

师：还想挑战吗？

生：（情绪高昂地说）想！

师：1/4除以2是多少？谁能上来结合图片说一说？

生：（有所领悟大声喊）我们把1个1/4替换成2个1/8，2个1/8平均分成2份，1份是1个1/8，就是1/8。

师：大家都太厉害了！我要给你们一个大大的“赞”。分数单位中还蕴含着许多深刻的奥秘，下课后，你们可以自己制作一些卡片玩一玩，摆一摆，说一说。

以上教学片段中，通过移一移、摆一摆、说一说等方式，把分数单位与分数运算有机结合起来，将分数单位隐性拓展到分数的四则运算中，表面上没有直接写出分数四则运算的算式，实质上讨论的几个问题就是分数的四则运算，“几个几”本质上是分数乘法，“多多少”“少多少”本质上是分数加、减法，“平均分成2份，1份是多少”本质上是分数除法，“把大单位替换成小单位”本质上是通分。这样通过数形结合的方式，学生直观感受分数单位在分数四则运算中的作用，体验数的认识与运算的整体性，感悟运算的一致性，学会用数学的眼光（分数单位）观察现实世界，用数学的思维（推理）思考现实世界，用数学的语言（分数单位）表达现实世界，有效促进核心素养的形成和发展。

【本文系课题“协同理论视域下UGSS合作职前职后教师职业能力整体性发展模式研究”（编号：FJJKBK22-062）的阶段性成果】

（作者单位：泉州师范学院教育科学研究所）