以大问题驱动 促进深度对话

【教学过程】

一、单元教学，直揭课题

师：同学们，今天我们将走进一个新的单元“分数”。之前我们认识了很多整数1、2、3、4……也用得很好，看到“分数”这个课题，你认为我们今天需要解决什么问题？

生：我想知道什么是分数。

生：分数与整数到底有什么区别？

师：这些问题问得太好啦！本单元，我们将分为三个部分。

生：（齐读）分数的初步认识、分数的简单计算、分数的简单应用。

师：这节课我们主要研究几分之一。（板书课题：几分之一。生齐读）课前同学们提问的问题太好啦，今天我们就主要研究“什么是分数？分数和整数有什么不同”。（板书大问题：一、什么是分数？二、分数和整数有什么不同？）

设计意图：以单元标题“分数”为主题整体建构，并揭示课题，以终为始，让学生明确本节课的学习目标。

二、话题推进，直指本质

话题一：知道半个是1/2。

师：其实认识几分之一，就是通过在生活中分东西来研究。同学们请看，（课件出示问题）老师这里有4个月饼，我们要平均分给2个同学，该怎么分？

生：每个同学分2个月饼。

师：为什么要每人分2个月饼？

生：因为要平均分，每人分得同样多，所以每人分2个月饼。（教师板书：2）

师：现在只有2个月饼，还是平均分给2个同学，怎么分呢？

生：老师，我知道，每个同学分1个月饼。（教师板书：1）

师：仔细看，现在老师只有1个月饼了，怎样平均分给2个同学呢？

生：老师，可以把月饼分成两半，一人一半。

师：这个说法很好哦，还能用整数来表示吗？

生：不能。

师：请你拿出月饼模型来折一折吧！看看这一半，我们该用一个什么样的数表示。

（学生折月饼模型表示1/2）

师：时间到，我请这个同学来说一说他是怎么折的。

生：同学们请听我说。（其他学生：我听你说）我把这个月饼分成了2份，我是从中间竖着对折这个月饼模型，2个同学吃这个月饼，就可以发现他们一人一半，吃的就同样多。

师追问：可以用一个什么样的数来表示呢？

生：1/2。

师追问：1/2你们听说过吗？到底怎么写呢？（板书：1/2）

师追问：那你能说一说这个1/2表示什么意思吗？

生：我是这样想的，有1个月饼，把它平均分成了2份，每人都得到了一半。

师追问：你的1/2是从哪里知道的呀？

生：老师，我是通过课前预习知道的。

师：哇，同学们，你们听到了吗？原来我们不仅可以通过书本学习，还可以通过课前预习。真是一个善于发现的小朋友，请把掌声送给她！

设计意图：在具体情境中，唤起学生对于“平均分”的知识。“平均分”是建立分数概念的重要因素，通过分月饼让学生经历分数的产生过程，初步感知半个就是二分之一。

话题二：说一说1/2表示的含义。

师：到底什么是1/2呢？能不能把你们分月饼的过程说出来？不用怕，老师来教你们。（师示范，边说边做手势，学生齐说）把1个月饼平均分成2份，每份是它的二分之一。（板书过程）

师：同学们想一想，我们刚刚干了什么事？与小组同学一起说一说。

生：我们刚刚把1个月饼平均分成2份，每份是它的二分之一。

师：同学们，二分之一该怎么写呢？

师：其实刚刚这个同学的分数写得正确，但是书写的顺序不对。数学上像这样的半个月饼，（书空准备）我们先写短横线，在分数当中叫分数线，表示平均分；在分数线的下面写2，叫分母，表示平均分成2份；在分数线的上面写1，叫分子，表示取其中的1份（师板书过程）。读作：1/2。（学生齐读）

师：每份是什么意思呢？

生：每份就是指这整个月饼的1/2，这1份也是整个月饼的1/2。（学生边指边说）

师：1个月饼有几个1/2？

生：（齐）有2个1/2。2个1/2合起来又是1个完整的月饼。

师：你们可太厉害了！

设计意图：通过实物操作活动，让学生尝试动手操作折一折月饼模型，进一步理解1/2的含义，加深学生对于[12]的理解。

话题三：认识1/4。

师：现在又来了2个同学，还是分这个月饼，怎么用分数来表示呢？再次折一折月饼模型，并与你的小组同学说一说吧！

（学生展示分享）

生：我是先把月饼模型竖着对折，然后横着对折，这样就可以得到[14]的月饼啦。

师追问：你能像刚刚那样完整地说一说吗？

生：把1个月饼平均分成4份，每份是它的四分之一。（教师板书过程）

师追问：这1份代表它的1/4，这1份呢？（生：也代表它的1/4）这1份呢？（生：也代表它的1/4）这1个月饼里面有几个1/4呢？（生：4个1/4）那4个1/4合起来会怎么样？

生：又是1个完整的月饼。（教师板书）

师：仔细观察这两种分法，有什么不同呢？与你的同桌说一说吧。

生：我是这样想的，它们的不同点是：一个是把月饼平均分成了2份，一个是月饼平均分成4份。它们的相同点是：都取了其中的1份，每份都是这个月饼的几分之一。

师：这个同学说得太好啦！掌声送给他！

设计意图：再次折同一个月饼模型，并完整地说出1/4的含义。在经历两次分月饼过程的对比中，再一次加强分数含义的表达，建立几分之一的分数模型。

话题四：认识1/3。

师：看，老师手里有1个圆，这个圆蕴含着什么分数呢？

生：把1个圆平均分成3份，每份是它的1/3。

师：你说得可真完整，请坐！

师追问：（边指板书）这1份呢？（生：是它的1/3）这1份呢？（生：是它的1/3）这个圆形里面到底有几个1/3呢？（生：3个1/3）3个1/3合起来又得到了什么呢？（如图1）

设计意图：通过经历实物到图形，学生建立几何直观，充分感知从整体到部分的关系。

话题五：认识1/5。

师：我要考考你们，老师这里有1个长方形，要想涂出长方形的1/5，想一想，首先要做什么呢？

生：首先要把这个大的长方形平均分成5个相同的小长方形。

师：这个同学说得真好！首先我们要把它平均分。有几种不同的涂法呢？请拿出学习单涂一涂吧！（学生拿出学习单涂）

师：这5种涂法（图略）都可以表示长方形的1/5吗？你是怎么想的呢？

生：我是这么想的，首先把这个大长方形平均分成了5个小长方形，这5种方法都是涂了其中的1份，所以每张图片的涂法都表示它的1/5。

师追问：你能像刚刚这样完整地说一说吗？

生：把1个长方形平均分成5份，每份是它的1/5。

师：这个同学说得非常好！是的，把这个长方形平均分成5份，每份是它的1/5。其实这个长方形的任意1份，都表示这个长方形的1/5。

师：我们刚刚分了月饼又分了图形，这4句话有什么相同的地方和不同的地方吗？与你的小组同学说一说吧！（小组交流）

生：我发现了它们分的数量都不同，第一个是平均分成了2份，第二个是平均分成4份，第三个是平均分成了3份，第四个是平均分成了5份。分的数量越多，每份就越小。

生：我发现它们都是平均分，都是取其中的几分之一。

设计意图：本环节通过涂一涂表示几分之一，增强对“平均分、每份、是谁的”的认识。

话题六：生活中的分数。

师：生活中也有几分之一这样的分数，与你的同桌说一说吧！

生：老师，我是把1个蛋糕平均分成7份，每份是它的1/7。

生：把1个西瓜平均分成8份，每份是它的1/8。

生：把1块饼干平均分成6份，每份是它的1/6。

师：其实生活中有很多用几分之一来表示的分数。我们一起来欣赏一下吧！（播放视频）同学们，再与你的同桌说一说生活中的几分之一吧！

三、创造分数，拓展延伸

话题一：分数和整数有什么不同？

师：我们刚刚了解了生活中的分数，分数和整数到底有什么不同呢？与你的小组同学说一说吧。

生：我发现，整数没有分数线，分数却有分数线。

生：我发现，分数是把一个东西分成很多份，但是整数不能分的时候，要用分数来表示。

师：是的，你们总结得非常好！当我们分物体或图形后不能再用整数表示时，就要用分数来表示。

设计意图：引导学生关注部分与整体的关系，意识到分数与整数最大的不同。

话题二：拓展延伸。

（1）判一判。（略）

（2）创造分数。

师：同学们，下面我们要先折一折、涂一涂，再像这样说一说。（做手势让学生知道怎么说）现在请拿出老师课前准备的图形折一折吧！（学生折完贴在黑板上，并说一说）

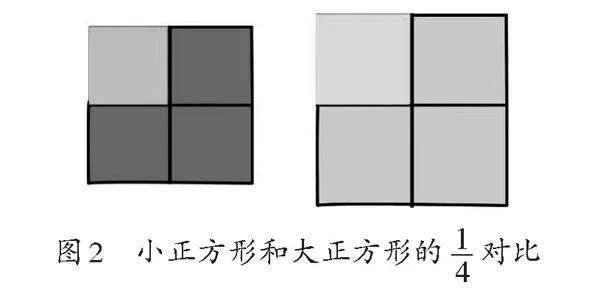
师：时间到。同学们创造的分数可真精彩呀！我要考考你们，这两个图形（如图2）表示的是几分之一呢？

b

生：老师，我发现是1/4。

师追问：为什么都可以用1/4来表示呢？

生：因为它们都是平均分成了4份。

师追问：都是平均分，但是图形的大小不一样呀？

生：虽然图形有大有小，但是它们都取了其中的1份。

师追问：是的，这个同学观察得很细心哦！（指大正方形中的1份）那这个是谁的[14]呀？

生：这个是大正方形的1/4。

师追问：那这个（指小正方形中的1份）是谁的1/4呢？

生：这个是小正方形的1/4。

师：大正方形取的1份和小正方形取的1份谁大谁小？

生：大正方形取的1份比较大，小正方形取的1份比较小。

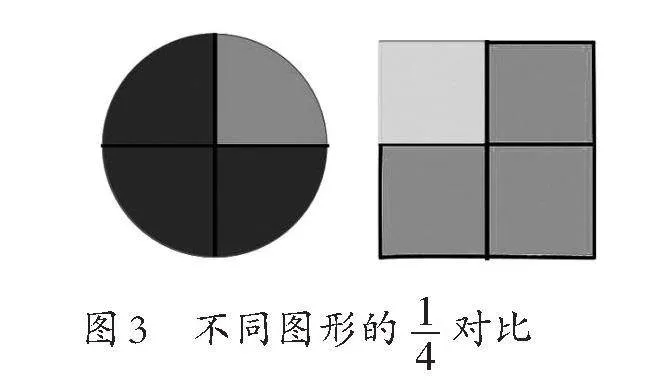
师：同学们请看这两个图形，（如图3）用什么分数来表示呢？（生：1/4）

师追问：不同的图形为什么都能用1/4来表示呢？

生：因为都是把图形平均分成了4份，取的都是1份，每份是它的1/4。

师：看来图形虽然不一样，但是我们可以用同样的分数来表示。

设计意图：本环节打破了学生对整数认知的经验，一是涂色部分形状相同、大小不同，可以用同样的分数来表示；二是涂色部分形状不同，也可以用同样的分数来表示，这就是分数的本质。

（3）猴哥和八戒分饼问题。

师：猴哥和八戒也遇到了同样的问题，我们一起来看看吧！（图略）猴哥吃了——

生：猴哥吃了剩下的1/2，我吃了我剩下的1/2，都是1/2，这下吃的可一样多了吧？

师：与你的小组同学说一说，看看八戒说的对不对。

师：我们请第六小组来分享一下他们的讨论结果。

生：同学们请听我说。（其他生：我听你说）是的，他们吃的不一样多，因为八戒的饼小一点，猴哥的饼大一点。猴哥的饼大，所以猴哥取的1份一定比八戒取的1份要多。

师：你们同意吗？这个同学说得太好啦，掌声送给他！我要考考你们，怎样让他们吃的同样多呢？与小组同学一起交流一下。

师：谁来说一说你有什么好方法？

生：把猴哥和八戒的饼都平均分成2份，猴哥的饼给八戒，八戒的饼给猴哥一半，这样猴哥和八戒吃的就同样多啦！

生：只要猴哥把他大饼的周围去掉，变成跟八戒的饼一样大小，这样就可以和八戒的饼一样多啦！

生：先不吃猴哥的饼，把八戒的饼分一半给猴哥，这样猴哥和八戒吃的就同样多啦！

师追问：这个同学说得太精彩了。他说就先吃八戒的饼。那还可以先吃谁的呢？

生：还可以先吃猴哥的饼，把猴哥的饼一人一半。

师：好办法，你们已经帮助他们解决了这个问题。

师：今天这节课你们学会了什么呢？

生：我们学会了把1个图形平均分成几份，每份是它的几分之一。

生：我们知道了什么是分数，整数和分数有什么不同。

……

师总结：今天我们主要学习的就是——（生：几分之一）接下来我们将学习几分之几，以及分数的大小比较和分数的计算。我们一起来期待下面的课吧！好，下课！

【教学反思】

本节课“分数的初步认识”以“大问题”为引领，“小话题”推进，促发课堂上的生成对话。以单元整体教学为目标，立足分数的本质，把课堂还给学生，让学生在充分的动手操作中，不断与整数对比，激发学生的学习兴趣。在教学过程中，渗透数形结合的思想，发展学生的数感和符号意识，实现数概念的扩展。

1.本节课是数学概念的一次扩展，学生在日常生活中有所了解，但是大多数学生只是部分了解，并不理解到底什么是分数。所以本节课我们设计了两个大问题：什么是分数？分数和整数有什么不同？通过两个核心问题带动学生思考，以“以问题驱动，促进深度对话”引领学生带着问题思考，带着问题交流。

2.对于三年级的孩子来说，结合实际进行分数含义的表达，“平均分、每份、是谁的”这三个关键点，是学生完整表达分数含义的难点。本节课通过折一折、涂一涂、说一说等操作活动，让学生充分表达分数的含义，通过直观操作帮助学生建立几分之一的分数模型，通过语言描述培养学生的表达能力。

3.本节课的创新点。按照课本上的编排进行教学，从分月饼到分图形，培养学生的几何直观能力，引导学生关注整体和部分的关系。但我们在创造分数这一环节中，设计一样的图形一个是大一些的，一个是小一些的，进一步通过描述分数时表达“是谁的”这一难点的突破，从而让学生明白分数与整数最大的不同。在八戒和猴哥分饼的过程中，发散学生思维，激发学生学习兴趣。

（作者单位：广东深圳市教育科学研究院，东莞市博立雅外国语学校）