经历数学化全过程，发展数学模型意识

新一轮的课程方案倡导深化学科实践，数学教学要让学生像数学家“做数学”那样参与全过程的数学化活动。在这样的过程中，学生用数学的眼光实现从现实世界到数学世界的转化和抽象；用数学的思维把复杂的问题变成相对好处理的数学关系与推导；用数学的语言（模型）建立现实与数学以及数学内部世界的结构关联，揭示普遍规律。数学课程所孕育的素养之果，正是学生经过这样的数学化活动之后所积淀和升华的产物，核心素养养成的关键是学会数学化。

下面我们以体育“比赛场次”问题开展综合实践活动，探究其数学化的路径是什么、数学化层次与表现差异如何以及如何设计和实施学生经历再创造的学习路径。

一、“比赛场次”问题的数学化本质是模型化

从数学化的角度来看，学生一般从某个具体情境的“比赛场次安排”问题出发，到探究两类赛制下的参赛队伍数与场次数的关系，最后概括出一般算法模型，其实质就是模型化的过程。所谓模型化，就是用模型把复杂的现实和理论理想化、简单化，从而更易于进行形式的数学处理的过程。在小学阶段，数学模型一般指的是：根据已有的实际问题，用字母、数字及其他数学符号建立起来的代数式、关系式、方程、函数、不等式，以及各种表格、图形等。

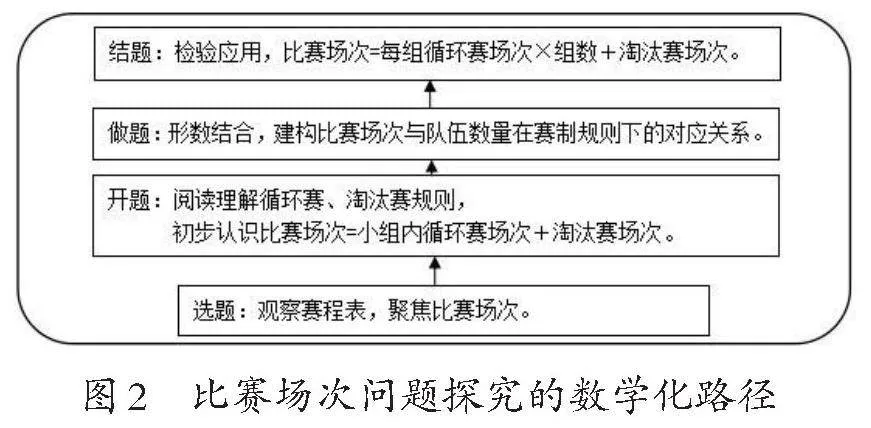
在建立模型活动中学生数学思维进阶表现可划分为四个层次：（1）情境层次。通过观察某项比赛日程表，对不同对阵场次的合理性安排产生好奇和疑问，由此提出比赛场次问题。（2）指涉层次。通过阅读材料初步理解循环赛、淘汰赛规则，运用模拟、列举、列表、画图等非正规方法，研究单循环赛、单淘汰赛赛制下比赛场次问题。（3）普遍层次。运用结构化的图表解决问题，以及在图表基础上抽象出算法和算式，以便解决同类问题。（4）形式层次。进一步形成一般的代数表达式。比如，单循环赛的场次数算法本质上是：从n队中任取2队的组合数，即场次数=[n×（n-1）÷2]。对于单淘汰赛，则是运用“二分法”，从n队中每次选一半，直至只剩1队，淘汰（[n]-1）队，场次数=[n]-1。可运用上述算式或代数式解决类似情境中的比赛场次问题，以及迁移思考新情境下的问题。其数学思维表现为由低到高的四个层次进阶（如图1）。这里的情境层次和指涉层次侧重从现实背景到数学问题的水平数学化，普遍层次和形式层次侧重在数学内部的垂直数学化。

基于探究比赛场次问题的数学化路径，学生学会运用直观图或列表建立实际情境与数学问题间的结构关系，深化理解算法的现实意义和价值，有助于发展几何直观和模型意识。

二、分析学习起点与设定学习目标

关于比赛场次，学生能否提出有价值的数学问题？为此我们对12名学生做了学前调研。其中有10人问到“比赛场次和数学知识有什么关联”，足见学生有寻求体育与数学的联系，调动已有知识经验开展研究的意识；有9人问到“场次数如何计算”或“有公式吗”，可见提供适切的现实情境，可以触发学生朴素的数学眼光，提出基本的数学问题；有7人提到研究比赛场次“有什么用”这样的价值叩问，有利于促进学生体会用数学的语言理解和表达现实世界的工具价值。还有学生提出：什么是比赛场次？比赛场次与什么有关，有什么关系或规律？怎样合理安排比赛场次？比赛场次在生活中有哪些应用？

此外，图示化、直观化是儿童数学化常用的表现方式，也是儿童数学化走向模型化的基础。在分析、解决问题过程中，学生能够调用“数线段”“枝形图”等经验通过直观图分析抽象的数量关系。

由以上分析确定本次实践活动的学习目标：（1）结合体育比赛赛程，了解赛程安排的基本结构，了解循环赛、淘汰赛规则。（2）能用列表、画图等方式探究分组循环赛、淘汰赛规则下比赛场次和参赛队之间的关系，并用适切的数学语言表达关系。（3）经历发现与提出数学问题、用数学方法分析与解决问题的全过程，感悟数学与实际的联系，发展模型意识。

三、比赛场次数学化路径——建模流程设计

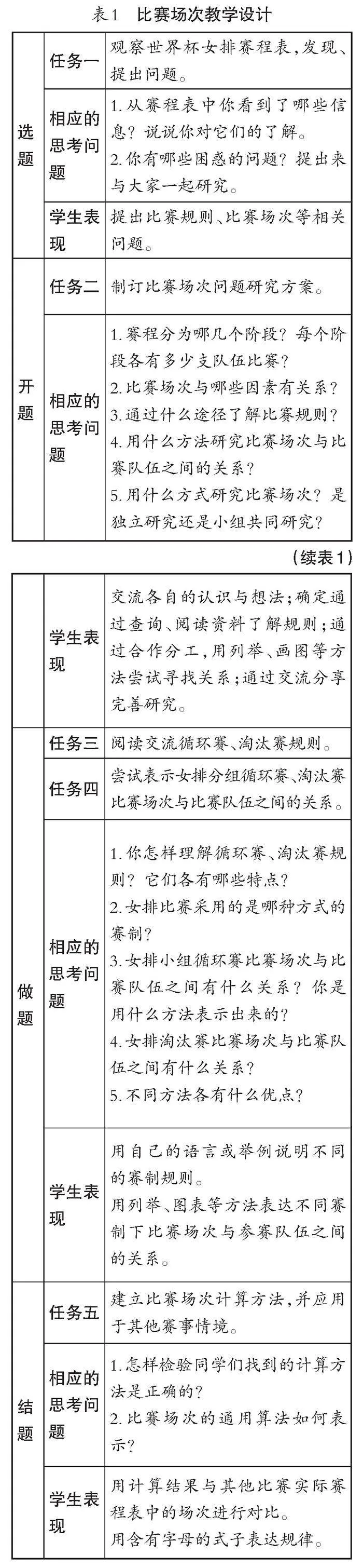
对比赛场次模型的建立与应用，是一项研究性学习活动，需要依次经历选题（提出问题）、开题（寻找问题要素并认识要素）、做题（尝试构建要素间的结构关系）、结题（检验、调整和应用规律解决问题）四个阶段。比赛场次建模的数学化路径如图2所示。

学生从对赛程表的观察到证实“比赛场次=每组内循环赛场次×组数＋淘汰赛场次”，中间需要重点探究单循环、单淘汰规则下比赛场次与参赛队伍之间的对应关系，并从图示化提升到形式化。这个过程需要教师引导和帮助学生用数学的方式方法对已有经验或认识进行再组织，实现学生的再创造。这里的引导、帮助主要体现在对任务链、问题链与学生预期表现的整体设计当中，引导学生操作材料与数学思考交融并进，促进数学化进程。本课任务链与问题链见表1。

通过对任务的操作，伴随问题的思考，学生对比赛场次的数学化建模过程拾级而上，由初步到完善、由局部到整体、由具体到概括，最终通过检验获得数学模型。

四、比赛场次数学化建模路径实施中学生资源的运用

比赛场次数学化建模路径实施中，个体的数学化进程需要与集体学习相互交融，以促进由个体认知到整体共识、由特殊到一般、由具体到抽象的转化。

例如，小组循环赛场次的理解，不同学生用不同方法探究后，需要交流讨论，促进理解。

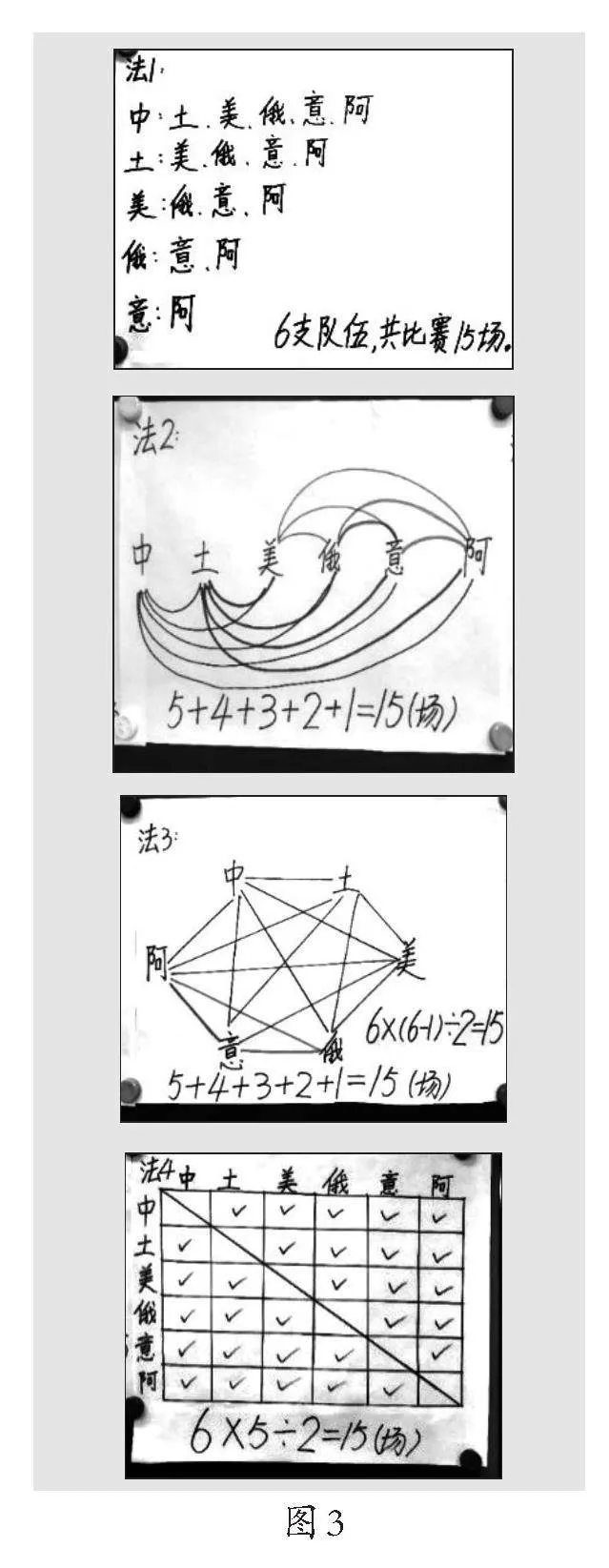
师：老师收集了4份成果，如图3。现在进入全班交流互动环节，要求看懂同学的方法、问明白你的疑惑、说出你的建议、表达对你的启发。

生1：方法4列表是我没想到的，也是比较简洁的，还能避免遗漏。

生2：我建议方法1、2、3在列举或画线过程中，把每次产生的场次数标出来，这样就更清楚了。比如中国与土、美、俄、意、阿，产生5场比赛……

生3：方法3中的算式6×（6-1）÷2=15和方法4中的6×5÷2=15我看不懂，谁能帮帮我？

生4：我来结合方法4解释，横着看，每只球队要与其他5支球队各打1场，我们看第2行（自上向下数）土耳其与中国这场比赛就重复了，因为第1行已经有中国对土耳其了。照这样，以对角线为对称轴，两侧的场次都是重复的。这样得到的是双循环的场次数，所以要除以2。

师：真好！通过交流，同学们在方法上获得启发；在交流过程中理解了单循环赛制，看到了场次与队伍数之间的关系；在讲解中厘清了算法。老师也有个疑惑，怎样确定我们找到的关系、算法是正确的呢？

生5：这好办！我们算出中国队所在小组是15场，另一个小组也是15场，共30场。这与赛程表（表略）列出的小组赛场次是一致的，所以我们（找到的关系和计算方法）是对的。

师：谢谢你！你让大家看到了严谨地思考问题和一丝不苟地做事的过程。于是，老师还想知道如果是8、9、10……支球队，怎样解决类似场次的问题呢？试着把你的方法写出来。

师：有不少同学列出了式子，写的是“队伍数×（队伍数-1）÷2”；也有些同学写的是“n×（n-1）÷2”。对这些不同的写法，你们怎么看？

在交流、欣赏、质疑、讨论中，学生对比赛场次的数学思维从感性具体（中国队要与其他每个队进行1场比赛）发展到感性一般（每队都要与其他队进行1场比赛），从理性具体（6×5÷2）发展到理性一般［n×（n-1）÷2］。

五、对比赛场次数学化建模过程的反思与迭代思考

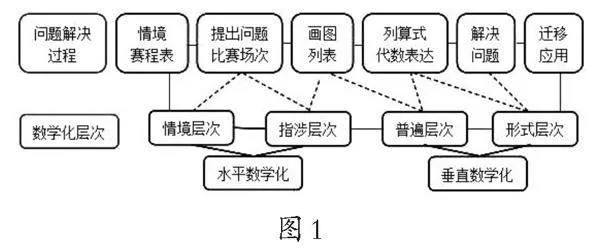
通过任务链的逐步实施，伴随问题链的推进，思维不断深入，数学模型从粗糙的猜想变成严谨的算法，在教师设计的学习路径的引导下，学生收获知识、研究方法、经验的同时，更收获了用数学思维、数学语言解释体育比赛规则的综合素养。如图4是不同学生的感悟与收获。

反思问题1：从普遍层次的算法化到代数表达的模型化过渡、从普遍层次到形式层次的发展过程中，给学生“悟”的时空不足。可以安排学生面对同一类新问题，让他们自由地选择数学化的表征形式去研究，从中感悟“队伍数”可以“任意”，在现实材料面前自然生成数学模型，向形式化进阶。

反思问题2：在归纳模型时，学生没有把循环赛、淘汰赛两阶段的算法合并的意识。这可能缘于小学生思维链较短，或者我们的路径设计还存在缺失。

如果将探究比赛场次的综合与实践活动过程拉长为2课时，让学生更从容地经历充分的数学化过程，尤其是有机会面对不同“面目”的实际情境，对于学生垂直数学化的发展会更有利，模型意识的发展会更自然。

【本文系北京教育学院2020年重点关注课题“基于数学项目学习的课程综合化实施路径研究”（编号：ZDGZ2020-20）的研究成果】

（作者单位：北京教育学院丰台分院，北京教育学院数学教育研究中心）