交通管控对新冠疫情传播的影响分析——以厦门市为例

刘博威, 刘晓佳

(1.集美大学航海学院,福建 厦门 361021; 2.集美大学海上交通安全研究所,福建 厦门 361021)

0 引 言

自2019年底以武汉市为中心的新冠疫情暴发以来,病毒传播对全国的生产生活都造成了极大的影响。为有效抑制新冠疫情,同时考虑到大规模人口的流动存在扩大疫情的风险,全国各地积极响应并采取相应的交通管控措施。为避免人口大规模流动,从停运市内客运站、火车站、飞机场以禁止人口跨市流动,到封闭市内道路以严禁非特殊车辆出行,再到封闭小区以控制小区内人口流动,都呈现出对疫情的不同阻断措施。同时,在不同时段采取不同的交通管制措施会对疫情的发展产生不同的影响[1]。因此,对新冠疫情下不同交通管制的有效性和时效性进行研究,可以为应对未来重大疫情暴发提供参考。

目前有许多学者都对新冠疫情的传播进行了深入分析。在交通管控策略及影响方面:姬杨蓓蓓等[2]通过典型相关分析和中介效应探究了不同影响因素与累计确诊人数之间的关系,发现经济水平、交通管控的强度和及时性对累计确诊人数影响较大;周继彪等[3]以宁波市疫情为研究对象,提出了基于问题驱动的非常规防疫策略,对多级组合的防疫策略进行调整,以最大限度地防止疫情传播。在传染病动力学和系统仿真方面,国内外不少学者针对新冠疫情传播的特点建立传染病模型来分析疫情传播过程:张宇等[4]建立了考虑沿公交线路传播疫情的改进易感者-潜伏者-感染者-康复者(susceptible-exposed-infected-removed,SEIR)模型,结果发现降低公交车辆上座率、加大乘客间的座位距离和加以通风消毒可有效降低乘客被感染的风险;蔡洁等[5]针对不同管控时效和不同管控强度建立了SEIR模型,结果发现各地政府应加快交通管控措施的实施来控制新冠疫情的发展;董章功等[6]将SEIR模型和自回归综合移动平均(autoregressive integrated moving average, ARIMA)时间序列模型相结合对不同时间段和不同地点的新冠疫情进行分析和预测,经对比发现SEIR-ARIMA模型拟合效果较好,对新冠疫情发展趋势的预测相对可靠;CARCIONE等[7]通过不断调整SEIR模型中潜伏者的潜伏期和感染者感染时间的上下限来分析意大利伦巴第地区的疫情传播情况;LYMPEROPOULOS[8]将易感者-感染者-康复者(susceptible-infected-recovered, SIR)模型与神经网络结合建立了Neuro-SIR模型,模拟社会网络中人与人接触中疫情传播的过程,结果发现Neuro-SIR模型对疫情的评估与预测有良好的效果,并验证了居家防控策略的有效性。

综上所述,以往学者对新冠疫情的传播特点进行了一定的研究,不仅证实了交通管控措施对阻断疫情发展的重要性,而且说明了传染病动力学模型模拟新冠疫情传播过程的有效性。然而,传统SEIR模型不能够准确表达出有交通管控措施下的疫情传播过程,并且随着时间的推移,疫情不断发展,交通管控强度及医疗措施等也会发生变化,这就导致了传统传染病动力学模型中的固定参数不符合实际情况。因此,本文对传统SEIR模型进行改进,不仅考虑到不同时间段、不同交通管控措施对疫情传播趋势的影响,而且将原来的固定参数改为时变参数。以厦门市2021年9月份出现的疫情为例,分析各种交通管控措施对疫情传播的阻断效果。

1 疫情趋势与交通管控措施

1.1 研究区域

交通方面的管理是新冠疫情防控中尤为关键的一环。全国各个城市都根据自身疫情暴发情况采取了不同程度的交通管控措施。厦门市2021年9月份出现的疫情新增病例数从有到无的起止日期为2021年9月12日—10月2日,感染者全部治愈的日期为2021年10月29日。考虑到新冠疫情具有潜伏期和传染性,设定研究时间从2021年9月5日—10月29日。累计确诊人数、日新增人数、累计治愈人数等疫情数据均来自厦门市卫健委。此次疫情防控过程中,交通管控措施实施及时,疫情经历的时间较短,有利于与无交通管控措施下的疫情传播趋势进行对比分析。

1.2 疫情传播及交通情况

厦门市自2021年9月12日起开始出现疫情,其每日新增确诊人数和现存确诊人数见图1。厦门市新增确诊人数从2021年9月12日起不断起伏,直至2021年9月20日之后才呈现稳定下降趋势。这一趋势延续到2021年9月28日,此时累计确诊人数达到高峰。2021年9月23日现存确诊人数达到高峰。随着交通管控措施和医疗措施的实施,感染人数逐渐下降,感染者也渐渐康复,直至2021年10月29日现存确诊本土病例清零。

图1 2021年9月5日—10月29日厦门市每日新增确诊和现存确诊人数变化

疫情暴发后,市内人口流动、交通出行对疫情传播存在极为负面的影响。通过百度迁移指数和百度慧眼统计的厦门市2021年9月份每日的迁移指数和出行强度指数见图2。图2中:迁移指数(包括迁入和迁出指数)反映的是城市人口迁入迁出的规模,是观测人员跨市流动的有效指标;出行强度指数是指城市有交通出行的人数与城市居民常住人口数比值的指数化结果。图2中迁出、迁入指数在2021年9月13日开始呈现下降趋势,出行强度指数从2021年9月15日起呈现下降趋势。为研究迁移指数和出行强度指数与新冠疫情传播的相关关系,将厦门市每日新增确诊人数分别与迁入指数和出行强度指数进行相关性分析,使用描述性统计进行相关系数检验,结果见表1和表2。厦门市每日新增确诊人数与10 d前的迁入指数具有较强的相关性,其相关系数为0.694(p<0.01)。厦门市每日新增确诊人数与6 d前的出行强度指数具有较强的相关性,其相关系数为0.702(p<0.01)。这说明在疫情前期迁入指数和出行强度指数的变化在一定程度上引起了一周左右之后的新增确诊人数同方向上的变化,这正好符合厦门市此波疫情大规模传播过程中感染人数变化规律。

表1 每日新增确诊人数与迁入指数的斯皮尔曼相关系数检验

表2 新增确诊人数与出行强度指数的斯皮尔曼相关系数检验

图2 厦门市2021年9月份每日的迁出、迁入指数和出行强度指数变化

1.3 交通管控措施实施情况

厦门市在此波疫情暴发初期,为避免人口大规模流动或聚集所导致的疫情传播加速,及时采取了相应的交通管控措施,其具体实施情况如下。自2021年9月14日起厦门市全市居民小区实行闭环管理,非必要不离厦,严格落实“测温亮码”措施;为预防和控制疫情,减少人员流动,降低疫情传播风险,9月15日起暂停了长途客运运营,同时停运厦门火车站部分列车和实行公交线路“跳站”运行;根据疫情防控实际情况,厦门市应对新冠疫情指挥部在9月18日又公布了第9、10、11、12号通告,封闭了所有娱乐场所、景区等公共场所,同时实施全市公交限行、快速公交系统(bus rapid transit, BRT)和地铁限流的防疫措施;为有效切断病毒传播途径,9月21日起厦门市实施全区道路封闭管理,禁止机动车通行(保障国计民生的车辆及疫情防控车辆凭证通行)。为更有效研究交通管控措施对疫情传播的阻断效果,将2021年9月15日左右的交通管控措施视为限制市内外人口迁入迁出的措施,将2021年9月21日左右的交通管控措施视为限制市内人群流动的措施。限制市内外人口迁移措施实施之后,迁出、迁入指数出现直线下降趋势,出行强度指数也逐步下降。限制市内人群流动措施实施之后,迁出、迁入指数和出行强度指数皆下滑至最低。

2 疫情传播模型构建

2.1 传统传染病动力学模型

对于大规模的传染病,弄清其传播过程,分析其传播规律和传播特征以控制和消灭传染病是非常重要的。一般可以建立微分方程模型来模拟传染病的传播过程。传统传染病模型有易感者-感染者(susceptible-infected, SI)模型、易感者-感染者-易感者(susceptible-infected-susceptible, SIS)模型、SIR模型、易感者-感染者-康复者-易感者(susceptible-infected-recovered-susceptible, SIRS)模型和SEIR模型,其中最具代表性的是具有潜伏期的SEIR模型。

SEIR模型将人群分为易感者、潜伏者、感染者、康复者等4类[9-10],其人数分别为S、E、I、R。SEIR模型对应的微分方程组为

式中:t为时间变量;N为人口总数,N=S+E+I+R;β为传染率;σ为潜伏者转换为感染者的速率[11];γ为感染者的移出率。

SEIR模型的状态转移见图3。

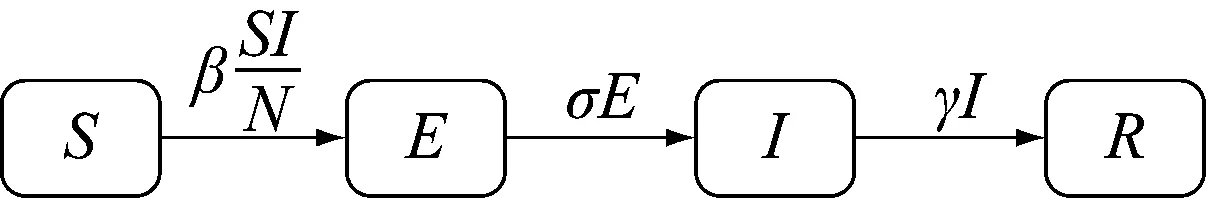
图3 SEIR模型状态转移

2.2 改进的SEIR模型

传统的SEIR模型中,潜伏者不具有传染性,但新冠病毒使潜伏者同感染者一样具有传染性。为此,将感染者的传染率记为β1,潜伏者的传染率为β2。这里的感染者包括确诊者和无症状感染者,故有I=I′+A,其中I′和A分别表示确诊者人数和无症状感染者人数。将确诊者的移出率记为γI′,无症状感染者的移出率记为γA。在新冠疫情暴发初期,由于潜伏者也具有传染性,故会对其采取相应的隔离措施。因此,将潜伏者划分为已隔离潜伏者和未隔离潜伏者,故有E=Eq+Enq,其中Eq和Enq分别表示已隔离潜伏者人数和未隔离潜伏者人数。在改进的SEIR模型中,人口总数不包含康复者,这是因为康复者不参与如图3所示的状态转移过程(由于康复者二次感染的概率微乎其微,所以不考虑康复者二次感染的情况),记改进模型中的人口总数为N′=S+Enq+Eq+I′+A。

在新冠疫情传播过程中,传染率和移出率等参数均会对模型产生影响,故参数的选取尤为重要。部分学者对模型参数的选取采用参考的方式,这种方法不够严谨,不同地区应对新冠疫情的措施存在差异,从而模型参数的选取也存在不同。本文通过粒子群(particle swarm optimization, PSO)算法拟合模型参数。PSO算法具有搜索速度快、效率高等优点,且应用于组合优化问题时能较好地找到问题最优解,其核心思想是在给定的解空间内进行搜索,找到一个解使得某个目标函数最大或最小。将拟合结果与实际数据的误差作为目标函数,通过PSO算法使误差达到最小,可以较好地拟合出模型参数。

2.2.1 参数设置

为使模型的结果更加贴合实际,结合厦门市此波疫情的实际数据,以及文献报道、专家意见、官方新闻等多方面信息对模型参数进行设置,见表3。需要外出的人口数为2021年厦门市人口数量的2%,潜伏者人数为7 d之后的新增累计确诊人数[11]。

表3 改进的SEIR模型参数设置

2.2.2 有人口迁移的SEIR模型(模型1)

在新冠疫情暴发前期,城市人口大量迁移,该迁移人群中就包含潜伏者,这极大地加强了病毒的传播风险。为更真实地模拟出无交通管控措施时疫情的传播过程,建立有人口迁移的SEIR模型(模型1),该模型的状态转移见图4。

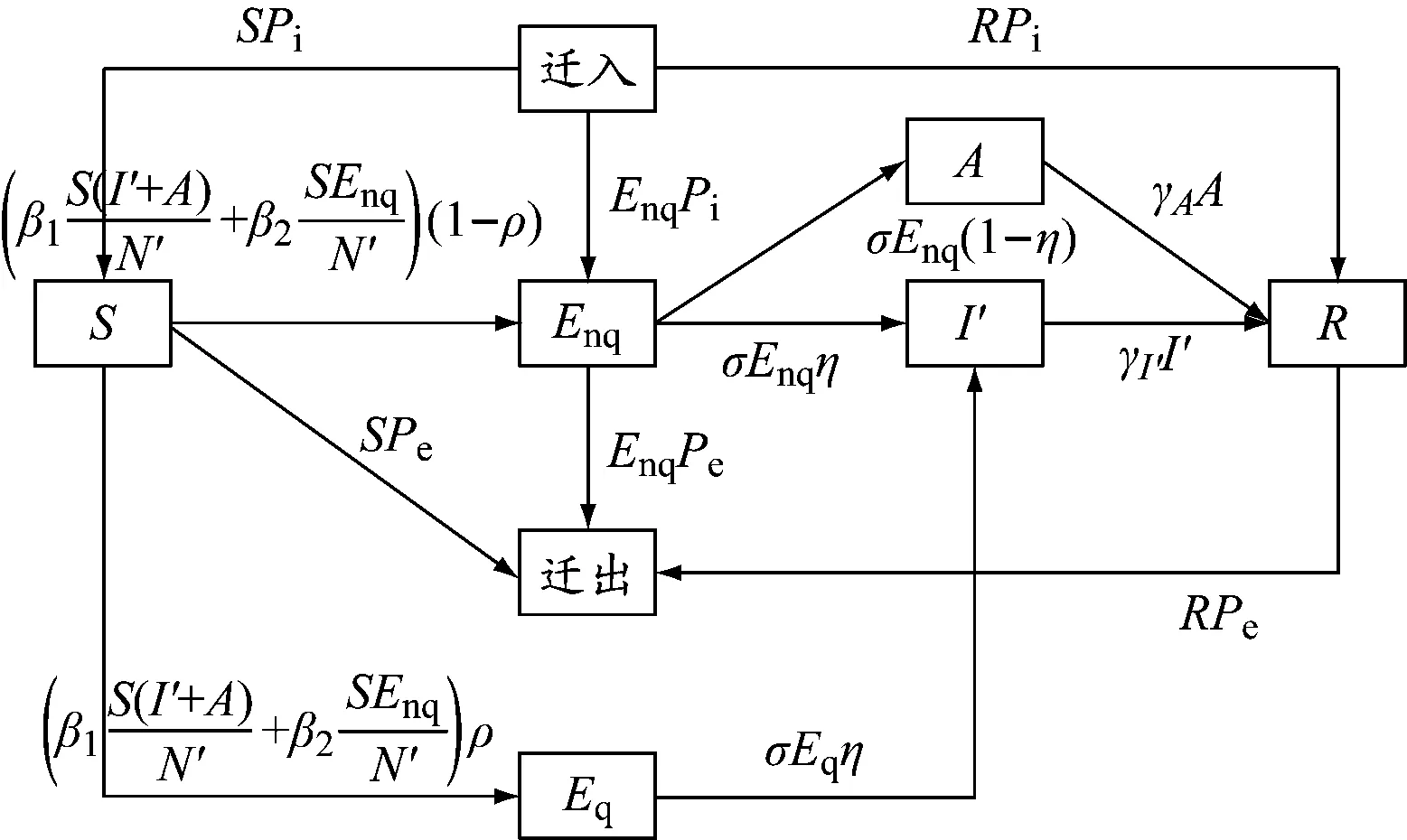
图4 有人口迁移的SEIR模型状态转移

模型1如下:

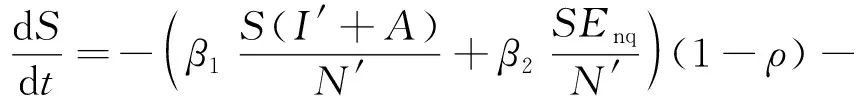
2.2.3 有交通限制的时变SEIR模型(模型2)

疫情来临时,通过实施限制市内人口流动的交通措施,可以减少人群聚集所导致的病毒传播,从根本上阻断疫情传播。通过限制易感者、潜伏者的外出范围和交通活动来减少病毒传播的可能性。建立交通限制仓室,属于该仓室的人群为因交通限制而不能外出的感染者、潜伏者,人数为L。

随着疫情的发展,在不同时间段需要采取不同的交通管控措施来阻断疫情的传播。因为传染率会随时间变化,所以根据传染率进行分段处理,在不同的时间段选用不同的传染率来建立SEIR模型。同时,感染者的移出率也不是一个固定的数值。疫情暴发后,随着时间的推移,医疗措施不断完善,外省医疗团队陆续支援,这使得移出率呈近似线性上升的趋势,故将感染者的移出率进行动态处理,使之成为一个与时间有关的函数。因此,本文建立有交通限制的时变SEIR模型,时变参数比固定参数更符合实际情况,从而可以更好地模拟疫情的传播过程。有交通限制的SEIR模型(模型2)的状态转移见图5。

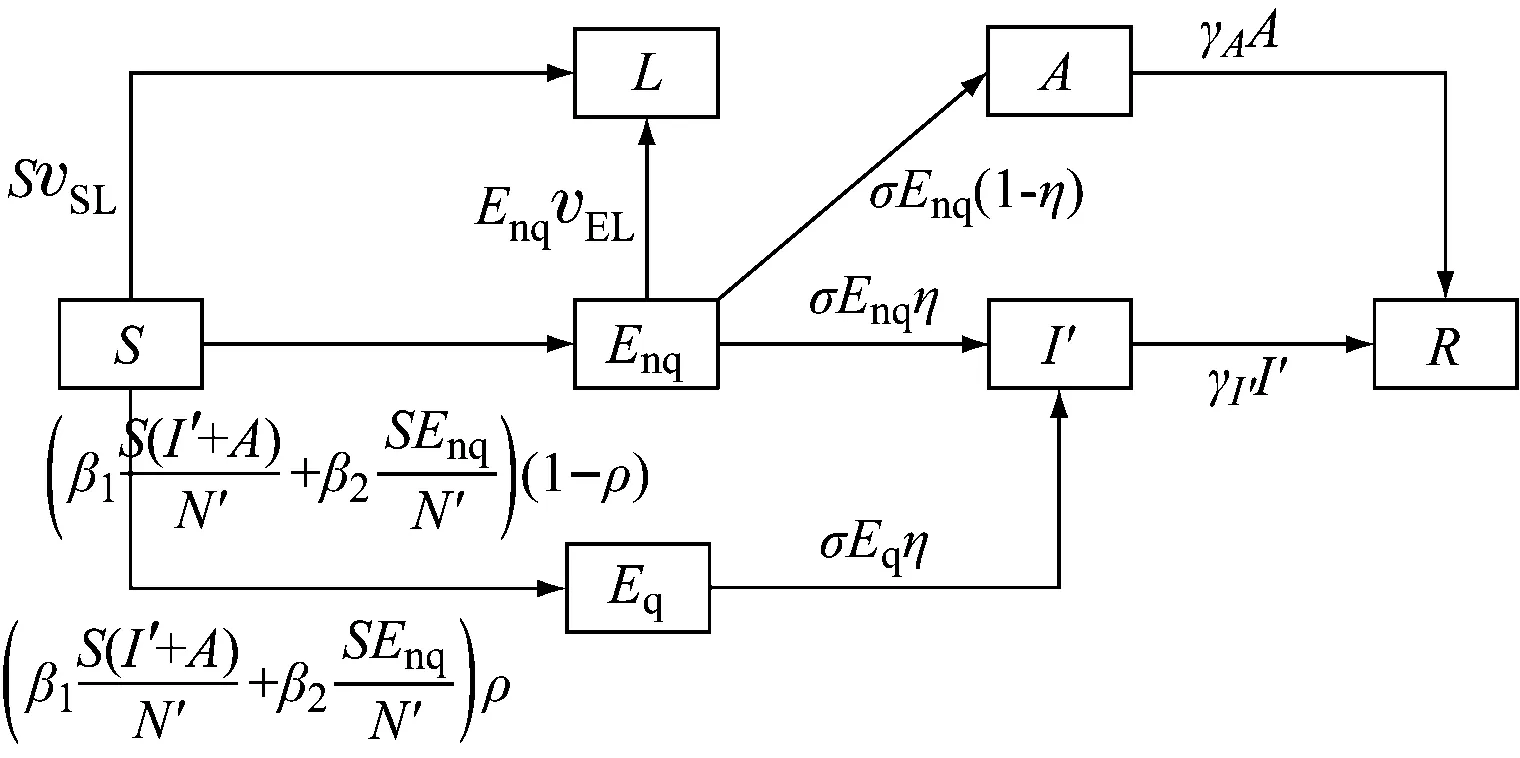
图5 有交通限制的SEIR模型状态转移

模型2如下:

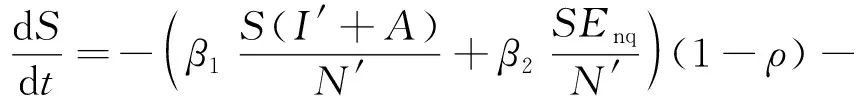
式中:β11、β12、β13分别为不同时间段内感染者的传染率;β21、β22、β23分别为不同时间段内潜伏者的传染率;t1、t2分别为采取相应交通管控措施时的时间分段点;a,b为移出率的动态参数。

2.3 模型评价

本文所搜集的数据来自厦门市卫健委,该数据均是在疫情暴发后厦门市政府在不同时间段积极采取相应交通管控措施后产生的。为验证模型的有效性,将模型2所模拟的疫情传播数据通过MATLAB拟合,由于潜伏者人数为7 d之后的新增累计确诊人数,将2021年9月5日(疫情开始7 d前的时间)作为疫情传播开始日期,第一次交通管控措施于2021年9月15日实施,第二次交通管控措施于2021年9月21日实施,所以令模型2中的t1=10 d,t2=16 d,通过PSO算法多次进行传播过程模拟,选取误差最小的一组数据,并将结果与厦门市实际疫情数据进行对比分析,结果见图6。模型2所模拟的感染者和康复者人数变化趋势、高峰时间与厦门市实际疫情大致相同,说明模型具有一定的可靠性。其中,所模拟的β11=0.585 9,β21=0.614 6,β12=0.010 1,β22=0.010 0,β13=1.090 9×10-6,β23=1.897 5×10-4,a=-0.080 0,b=0.005 2。每次模拟的结果具有随机性但变化范围不大。

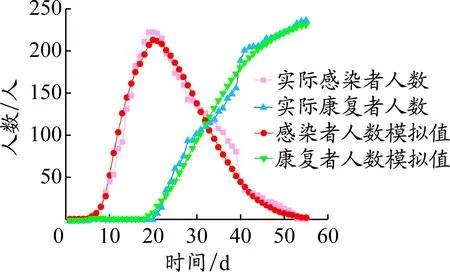
图6 厦门市采取交通管控措施后的疫情人数模拟值与实际值对比

为验证SEIR模型加入时变参数的效果,将模型2中的参数固定,即β1、β2、γI′、γA与时间无关,取消动态处理,计算后所得参数β1=0.002 7、β2=0.004 1、γA=γI′=0.102 0。将模型2和固定SEIR模型所得感染者人数、康复者人数与真实数据的残差平方和分别进行对比,结果见表4。可以看出,不论在感染者人数还是康复者人数方面,基于时变参数所得出的结果都比基于固定参数的更小,可知时变SEIR模型能更好地拟合出实际疫情传播趋势。

3 结果分析

3.1 无交通管控措施时的疫情传播趋势

疫情暴发后,厦门市对疫情在不同时间点及时地采取了相应的交通管控措施,达到了较好的防疫效果,避免了疫情的扩散。为对比分析有无交通管控措施对疫情传播的影响,根据图4和模型1模拟出疫情暴发后无交通管控措施时的疫情发展趋势,结果见图7。通过PSO算法得到β1=0.2,β2=0.507 0,γI′=γA=0.248 1。

疫情暴发前期,由于人口迁出的影响,感染者人数并没有急剧上升。随着疫情传播,且不采取任何交通管控措施,大约在疫情暴发三周之后,潜伏者和感染者人数急剧上升,历经66 d后感染者人数达到高峰,比有交通管控措施时的疫情高峰时间推迟了42 d。无交通管控措施时高峰感染人数为有交通管控措施时的将近50倍。此外,有交通管控措施时从发现首例病例到感染人数清零共经历了55 d,而在无交通管控措施时则需经历大约4个月。由此可见,在疫情暴发时,及时有效地采取交通管控措施对阻断疫情传播有明显的效果。

3.2 交通管控措施防疫效果对比分析

对此波疫情,厦门市政府在交通方面分别实施了2种措施来阻断疫情:措施1是限制市内外人口迁移;措施2是限制市内人群流动。为分析这两种交通管控措施阻断疫情的效果,推迟措施实施时间,模拟结果见图8。

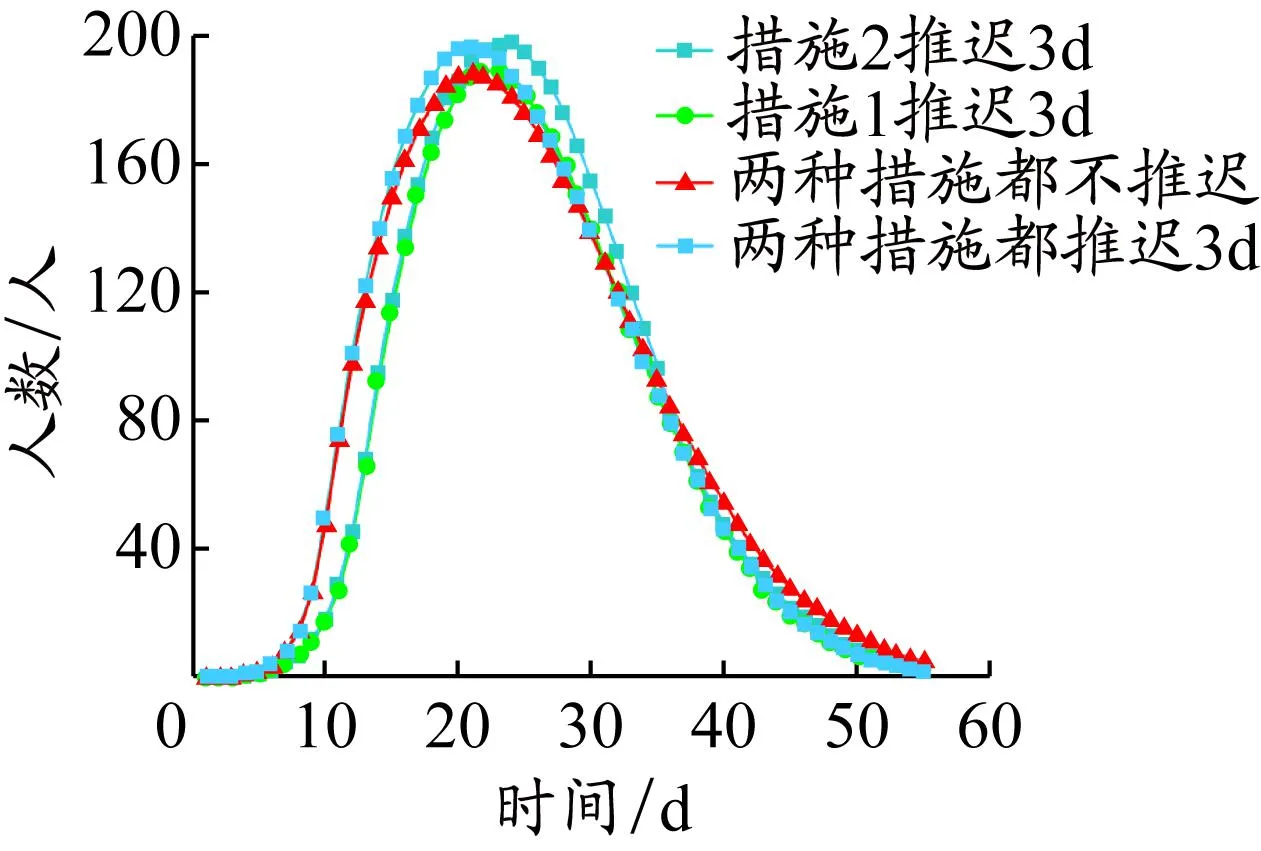
图8 推迟交通管控措施实施情况下的感染人数变化趋势

当措施1推迟3 d、措施2实施时间不变时,令模型2中的t1=13 d,t2=16 d,模拟发现感染人数到达高峰的时间滞后了2～4 d,由于人口迁出的影响,感染人数峰值并没有明显的提升。由此可见,措施1实施时间越早,感染人数到达峰值的时间越靠前。当措施1实施时间不变、措施2推迟3 d时,令模型2中的t1=10 d,t2=19 d,模拟发现感染人数峰值提高了约4.23%。由此可见,措施2实施的时间越早,感染人数的峰值就越低。若2种措施都推迟3 d,令模型2中的t1=13 d,t2=19 d,模拟发现感染人数达到峰值的时间延后,且感染人数增多。这表明在疫情来临时,越早实施交通管控措施,疫情的控制效果就越为明显,且综合实施交通管控措施对疫情的防控效果更显著。

4 结 论

将传统传染病模型改进为有交通限制的SEIR模型,模拟出不同交通管控措施下疫情的传播趋势,并以厦门市为研究对象,分析不同交通管控措施阻断疫情传播的效果,得到结论如下:(1)新冠疫情的传播与市内外人口迁移和市内交通出行强度有较强的正相关性。厦门市每日确诊新增人数与10 d前迁入指数的相关系数为0.694(p<0.01),与6 d前出行强度指数的相关系数为0.702(p<0.01),这表明交通出行强度对疫情的传播有一定的推动作用。(2)通过构建时变参数,使用PSO算法模拟出更符合实际情况的模型参数,并结合所选择的最优参数对疫情的传播过程进行建模。与传统传染病模型相比,改进的SEIR模型能够更好地模拟出不同交通管控措施下的疫情传播趋势。(3)对不同交通管控措施的疫情阻断效果进行分析,可以发现:及时实施限制人口迁移措施可使疫情达到高峰的时间提前;及时实施限制市内交通出行措施可使感染人数峰值降低;综合并及时实施各项交通管控措施对疫情阻断的效果最为明显。

新冠疫情传播是极其复杂的过程。本文仅使用了厦门市2021年9月份出现的疫情数据来构建模型,会导致结果可能存在偶然性和特殊性。综合多个地区的数据进行分析是未来研究的方向。