基于改进NSGA-Ⅱ的多式联运协同优化

尹传忠, 彭海红, 陶学宗, 张子昂*

(1.上海海事大学交通运输学院,上海 201306;2.招商局南京油运股份有限公司扬洋公司经营部,江苏 南京 210000)

0 引 言

长江是我国的“黄金”经济带,在我国经济发展过程中占据重要地位。多式联运不仅能够有效降低货物的运输成本,减少运输时间,而且能够提高运输质量,改善生态环境,助力“双碳”目标的实现。因此,在货物运输过程中要强化多式联运组织与管理能力,推进区域一体化绿色发展。目前,长江流域的运输能力持续增强,基本形成了完善的综合运输体系。长江沿线11个省市拥有180个港口和21 486个泊位(包含826个万吨级泊位),港口集疏运方式以公路运输为主,铁路、水路运输为辅。对2017—2020年长江经济带三大经济圈公路、铁路、水路3种运输方式的货运量进行统计发现,铁路运输占比较低,公路运输占比较高,运输结构不合理。随着我国长江经济带战略规划的出台,很多学者对长江经济带多式联运进行研究,如:陈宝丰[1]分析了重庆和武汉集装箱多式联运发展滞后的原因,提出促进集装箱多式联运发展的措施和建议;刘清等[2]建立综合考虑运输成本、时间、风险等因素的长江干线集装箱多式联运路径优化模型,并运用遗传算法进行求解;李敏[3]和康凯等[4]考虑多式联运运输量低、设施与设备之间连接不良等问题,建立了长江经济带集装箱多式联运优化模型,最后得出结论——铁路专用线进入港口不仅可以有效降低总物流成本,而且能够增强多式联运产品的市场竞争力。

在铁水联运模式方面:刘启钢等[5]对铁水联运系统利益相关方的关系进行博弈分析,提出了铁水联运生态模式运行机制;MOSTERT等[6]考虑经济和环保两方面的因素,将联合运输与单一公路运输进行对比,结果表明联合运输比单一公路运输更有优势;SEO等[7]采用成本模型对比了重庆到鹿特丹的7条运输路线,得出采用海铁联运可以降低运输成本、缩短转运时间;MOKHTAR等[8]设计了铁水联运的集装箱枢纽港选址模型,并利用印尼的真实数据验证模型的有效性。

在多式联运网络优化方面:黄丽霞等[9]考虑路段容量限制和货物送达时间要求,建立了以运输风险和运输成本最低为目标的多式联运路径优化模型。LUO等[10]提出了超大件货物多式联运路径规划的重构模型,并引入改进的K最短路径算法进行求解。随着“双碳”目标的提出,重点考虑碳排放成本的多式联运路径优化和网络优化问题相继被研究[11]。王清斌等[12]在多式联运网络中,建立以时间为约束、以总成本最低为目标的模型,并运用多蚁群并行算法进行求解。MARTINE等[13]提出了一种兼顾经济和环境的涉及公路、铁路、水路3种运输方式的联运网络。MENG等[14]和VAN ECK等[15]利用嵌入对角化的混合遗传算法研究多式联运网络设计问题;LEBEDEVA等[16]研究包含铁路运输和公路运输的多式联运成本优化问题,指出多式联运是代替公路长途运输的一种经济有效的运输模式;尹传忠等[17]构建了区域主枢纽港多式联运网络双目标协同优化模型,采用理想点法将双目标模型进行转化并求解,以实现长三角地区多式联运网络协同。

目前,对多式联运路径选择、运输方式选择、运输网络优化等方面的研究较多,它们从关注运输成本、运输时间拓展到运输的低碳程度、路径/网络可靠性、顾客满意度等。然而,现有研究在求解多目标模型时通常将多目标模型通过设置权重转化为单目标模型进行求解,对多目标模型直接进行求解及获得Pareto解的方法有待完善。本文在阐明长江经济带三大经济圈多式联运现状的基础上,建立以运输成本、运输时间和碳排放量最小为目标的多式联运协同优化模型。针对该多目标问题设计相应的改进算法,即:用理想点法代替带精英策略的非支配排序遗传算法(elitist non-dominated sorting genetic algorithm, NSGA-Ⅱ)中的拥挤程度算子,克服Pareto解集中个体分布不均和算法求解效率低的缺点;采用改进的NSGA-Ⅱ获得问题的Pareto解集,结合逼近理想解排序法(technique for order preference by similarity to an ideal solution, TOPSIS)从Pareto解集中选择最优的多式联运方案。

1 多式联运协同优化模型

模型假设:每个转运节点作业能力均能满足运输需求;同一批货物在运输过程中转运时不可分割;货物在整个运输过程中在每个转运节点只能转运一次,同种运输方式之间不进行转运。

模型参数及变量定义:I为运输节点集合,i∈I;K为运输方式集合,k,p∈K;ck,i,i+1为采用运输方式k从节点i到i+1的单位运输费用,元/(t·km);lk,i,i+1为采用运输方式k从节点i到i+1的运输距离,km;tk,i,i+1为采用运输方式k从节点i到i+1的运输时间,h;ek,i,i+1为采用运输方式k从节点i到i+1的单位碳排放量,kg/(t·km);e为在节点进行换装作业的单位碳排放量,kg/t;ci,k,p为在节点i运输方式由k转换为p的单位转运成本,元/t;ti,k,p为在节点i运输方式由k转换为p的单位转运时间,h/TEU;m为货物总质量,t;N为集装箱数量,TEU;cs为货物提前到达的单位存储成本,元/(h·t);tE为最早收货时间;tL为最晚收货时间;tT为实际收货时间;cP为延迟到达的单位惩罚成本,元/(h·t);Qi,j为由节点i运输到节点j的货流量,t;Qk,i为由运输方式k运输到节点i的货流量,t;Pi为节点i的货物处理能力,TEU/h;M为运输网络节点数量;xk,i,i+1为决策变量,若在节点i采取运输方式k将货物运到节点i+1,则其值为1,否则为0;yi,k,p为决策变量,若在节点i运输方式由k转换为p,则其值为1,否则为0。

假设有N个且总质量为m的集装箱需经长江经济带从出发地运到目的地,出发地和目的地确定,可以选择途经的任意城市作为中转点。模型以运输成本最低、运输时间最短、碳排放量最少为目标:

mcPmax(tT-tL,0)

(1)

(2)

(3)

s. t.

xk,i-1,i+xk,i,i+1≥2yi,k,p, ∀k,p∈K

(4)

tk,i,i+1≥0,ti,k,p≥0,m≥0

(5)

Tmin≤T≤Tmax

(6)

(7)

(8)

Qk,i=Qi,j

(9)

Qi,j≤Pj

(10)

式(1)为运输成本最低的目标函数,包括各路段的运输成本、在节点的换装作业成本、提前到达的仓储成本或延迟到达的惩罚成本;式(2)为运输时间最短的目标函数,包括节点间的运输时间和在节点进行换装作业的时间;式(3)为碳排放量最少的目标函数,碳排放主要指消耗燃油产生的CO2排放量[18],包括运输路段上的碳排放量和在节点进行换装作业的碳排放量;式(4)保证整个运输过程连续;式(5)保证运输时间、转运时间和运输量非负;式(6)表示货物运输和转运时间之和应满足运输时间窗约束,该时间窗为[Tmin,Tmax];式(7)保证在运输路线上的两个节点之间只能选择一种运输方式;式(8)表示运输过程中最大转运次数不能超过G;式(9)保证进出货物流量平衡;式(10)保证进入该节点的货流量不超过其最大处理能力。

2 算法设计

NSGA-Ⅱ是一种带精英策略和基于Pareto最优解的快速多目标优化算法,能够有效解决非客观的权重分配问题[19]。对于双目标问题,Pareto最优前沿通常是二维坐标系中的一条曲线;对于多目标问题,Pareto最优前沿通常被表示为空间中的超曲面。关于本文的多目标优化问题,Pareto最优前沿可视为由非支配解集决定的超曲面。在应用过程中,首先对所有方案进行非支配排序并淘汰那些被支配的方案。通过这种方式获得第一级非支配方案集合,再利用评价函数对该集合中的每个方案进行分析以获得最优方案。目前很多学者对NSGA-Ⅱ进行了改进,如将遗传算法与其融合[20]、设计贪婪变异算子[21]、使用均匀分布策略[22-23]等。利用理想点法[24]改进NSGA-Ⅱ的方法[25]也较多,但是将此改进算法用于求解多式联运最优路径的研究较少。本文利用理想点法对传统的NSGA-Ⅱ进行改进并用于求解多式联运最优路径,将原算法中的拥挤程度算子替换成理想点法。理想点法是一种多指标评价方法,借助于评价对象与理想化目标的接近程度来衡量其优劣。与拥挤程度算子相比,理想点法的评价功能可以克服Pareto解集中个体分布不均和算法求解效率低的缺点。该评价函数为

(11)

式中:Z*、T*、E*分别为目标Z、T、E的最优值,(Z*,T*,E*)即为理想点;y为实际值(Z,T,E)与理想点之间的距离。最优方案是实际值与理想点之间差距最小的方案,故评价函数值最小的为最优解。

算法步骤:编写模型程序和输入相关数据;计算单一目标的最优解;使用非支配排序方法对种群中的个体进行分层获得第一级非支配层,并计算每个非支配个体的3个目标值,确定各单一目标的最优值Z*、T*、E*,得到理想点;利用式(11)计算每个非支配解对应的评估函数值并进行比较,选取评价函数值最小的解作为多目标问题的最优解集;根据选出的最优解集以3个目标函数为评价指标,利用TOPSIS对各个解进行评价排序(见图1),最后得出排名前10的解。图1中,评价指标正向化处理公式中带角标的y分别表示Z、T、E。

图1 TOPSIS评估排序流程

3 案例分析

3.1 问题描述

长江经济带是我国货物运输的主通道,是“一带一路”在国内的主要交汇地带[26]。假设沿长江经济带有20个且总质量为400 t的标准集装箱需要从宜宾运往上海,运输时间窗为[36,120]h,提前到达的存储成本为40元/(h·t),延迟到达的惩罚成本为60元/(h·t)。根据多式联运网络构建原理,构建从宜宾到上海的多式联运网络,见图2。参考文献[2],设置铁路与公路的转运费用为5.5元/t,转运时间为0.2 h/TEU;铁路与水路的转运费用为7.5元/t,转运时间为0.45 h/TEU;公路与水路的转运费用为6元/t,转运时间为0.34 h/TEU。参考文献[27],设置铁路、水路、公路的运输成本分别为0.135、0.03、0.35元/(t·km)。铁路、水路、公路的运输速度分别为60、20、70 km/h[28]。

注:虚拟连接的点表示在现实世界为同一个点

3.2 案例求解

设置种群大小为200,最大迭代次数为500,交叉概率为0.8,变异概率为0.2。利用MATLAB R2018a对模型进行求解。图3和4分别为利用传统NSGA-Ⅱ和改进的NSGA-Ⅱ求解得到的最优Pareto解集,可以发现改进的NSGA-Ⅱ得到的3个目标函数值更小、更集中、更接近Pareto最优解集,故改进的NSGA-Ⅱ比传统NSGA-Ⅱ更有优势。

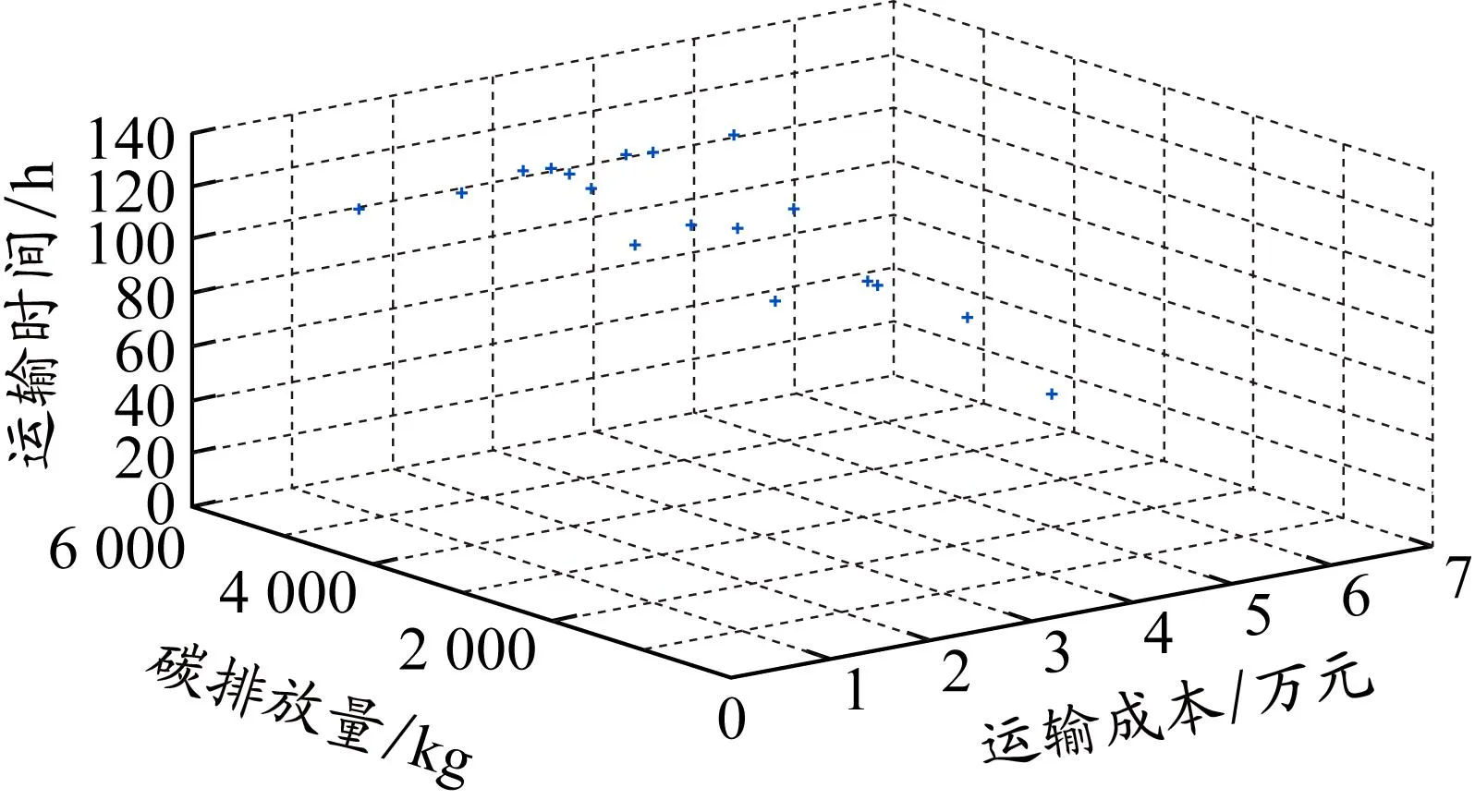
图3 传统的NSGA-Ⅱ求解得到的Pareto最优解集

图4 改进的NSGA-Ⅱ求解得到的Pareto最优解集

利用TOPSIS得到Pareto最优解集中排名前10的解,见表1。由表1可知:运输成本、碳排放量、运输时间这3个目标的最优解分别为32 962.8元、7 947.20 kg、137.35 h;重要度最高值为0.604 8,其对应方案即为最优方案(见图5),该最优方案的运输成本、碳排放量、运输时间分别为78 268.8元、8 678.38 kg、219.62 h。

表1 Pareto最优解集中排名前10的解

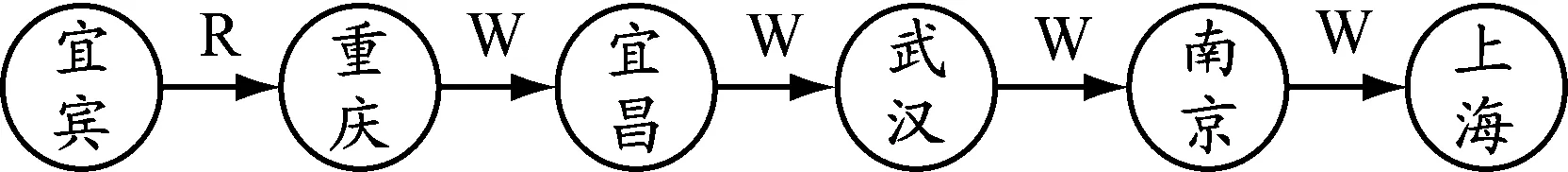
注:R、W分别表示铁路、水路运输

对排名前10的解求平均值,得到一个优化方案,将其与仅使用改进的NSGA-Ⅱ得到的初始方案进行对比,结果见表2。由表2可知,该优化方案与初始方案相比,运输成本降低16.98%,碳排放量减少2.39%,运输时间缩短5.79%,重要度增加了7.85%。

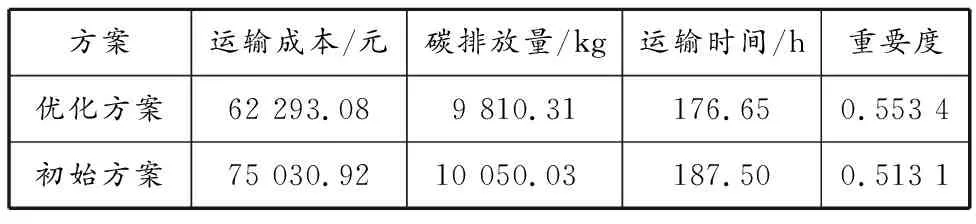
表2 优化方案与初始方案的对比

3.3 灵敏度分析

为研究转运效率对最优方案的影响,将集装箱的转运时间分为4种情景进行计算,每种情景下的最优方案见表3,每种情景下的运输成本、碳排放量和运输时间的变化见图6。

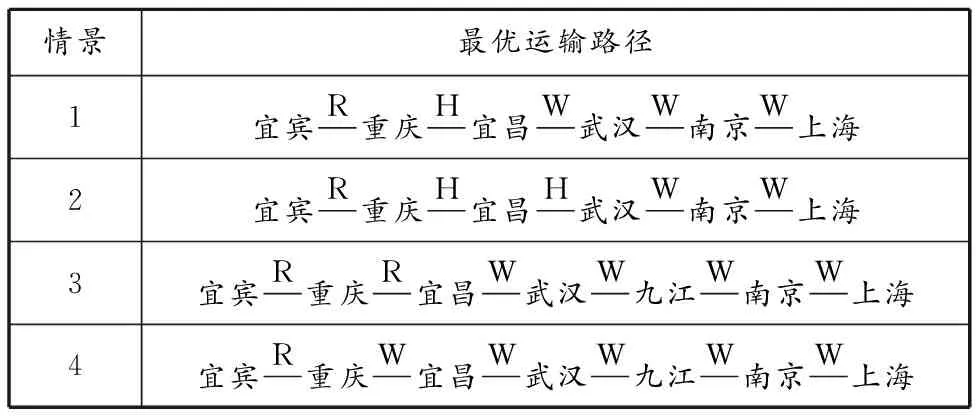
表3 不同转运时间下的最优方案

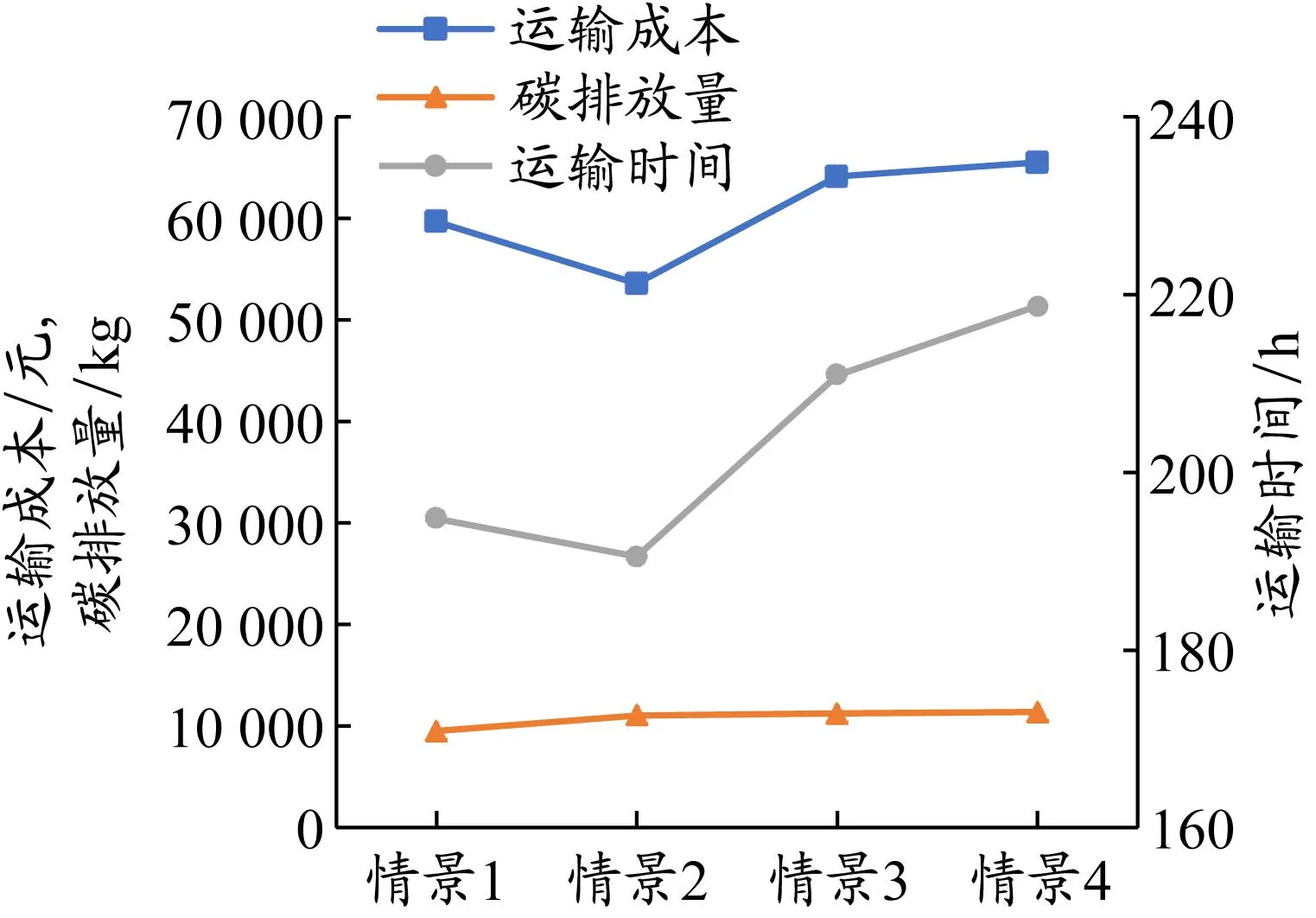
图6 不同转运时间下运输成本、碳排放量、运输时间的变化

情景1和2:转运时间分别缩短为设定的转运时间的1/5和1/2。在这2种情景下:与表1中单目标的最优解(运输成本32 962.8元,碳排放量7 947.20 kg,运输时间137.35 h)相比,平均运输成本增加了21 653元,平均运输时间减少了26.98 h,平均碳排放量减少了2 649.05 kg;与最优方案(见图5)相比,转运次数增加了1次。情景3和4:转运时间分别延长为设定的转运时间的5倍和10倍。在这2种情景下:与表1中单目标的最优解相比,平均运输成本增加了13 469元,平均运输时间增加了51.61 h,平均碳排放量增加了1 620.41 kg;与最优方案(见图5)相比,转运次数不变。结合表3和图6可知,转运效率越高,公铁联运的占比就越大,碳排放量就越少。因此,转运效率是影响多式联运的关键环节,提高转运效率及换装设备技术水平,对于促进多式联运系统节能减排十分重要。

4 结 论

从货物运输需求的实际情况出发,综合考虑联合运输中的运输时间、运输成本、碳排放量和货主时间窗,建立多目标规划模型,采用改进的NSGA-Ⅱ进行求解,优化长江经济带多式联运方案,得到如下结论:(1)提出一种NSGA-Ⅱ与理想点法结合的改进算法,解决了非支配解集包含过多解的问题,在保证算法精度较高的同时有效降低了运输成本、运输时间和碳排放量,为多目标问题求解提供新的思路。(2)在多式联运优化方案选择过程中,决策者可以根据问题的Pareto解集,选择最适合自身需求的方案,从多主体角度通过TOPSIS获得整个运输系统的最优规划方案。(3)在多式联运路径规划中,随着转运效率的提高,转运次数会增加,但总体运输时间变化幅度不明显,运输成本和碳排放量的变化较大。因此,转运效率的提升和转运设备技术更新对多式联运最优方案的选择和节能减排尤为重要。

多式联运是一个多变且复杂的运输过程,随着“双碳”目标的提出以及交通运输业对碳排放重视程度的不断提升,后续对碳交易价格不确定情形下区域多式联运网络优化,以及多式联运过程中排放的其他污染物(如氮氧化物、硫氧化物)对运输网络的影响的研究都很有必要。另外,本文并未考虑船舶在三峡大坝的待闸时间、船舶在港等待作业的时间等,造成求解所得时间与实际运输时间有差距,后续需要进行完善。