施托克豪森STUDIE II非平均律音阶模型与声音合成微探

史历伟

摘 要：作为当代著名的先锋电子音乐作曲家，施托克豪森的创作观念以及多元化的技术手段整合达到了新的维度。曲子《STUDIE II》以新的音阶模型打破了对于传统十二平均律听觉上的局限，并且尝试在新的音阶模型上对声音合成达到逻辑化的音色重塑。无论是传统的人工调式还是人工音阶，都基于十二平均律，并结合了逻辑性和随机性，而施托克豪森则在1954年模拟时代下，依靠有限的硬件设备计算出25律制，并且将其均等分，将其不同频率下的正弦波以加法合成的形式进行音色重塑，将其独有的音阶模型与声音合成进行多维度的融合，改变对固有的十二平均律听觉上的心理感受。

关键词：施托克豪森；十二平均律；非平均律音阶模型；声音合成；练习曲二（STUDIE Ⅱ）

中图分类号：J614文献标识码：A文章编号：2096-0905（2023）33-0-03

传统的调式音阶或是当代人工调式、音阶，都基于传统的听觉十二平均律，作曲家在“调性”与“无调性”作品之间相互交错，他们在传统的音阶调式上做逻辑化的音高材料组织。早期勋伯格的无调性音乐研究走向十二音的体系，同样梅西安的《我的音乐语言的技巧》中提出了有关人工调式概念的建立。再到后期德彪西、巴托克的对于人工调式的运用，横向对于人工调式内的音高动机细胞的使用，纵向音高音程和声构建都与十二平均律密不可分。

而对于平均律的概念早在古希腊时期便被提出，但当时并未合理地运算出结果，而到我国明朝时期朱载育根据数学来定制十二平均律。而在文艺复兴时期对于音准的概念还未被真正定義，早期大量的键盘乐器、乐曲调式调性层见叠出，这就导致音乐作品之间音高体系的割裂，每一首作品每一件乐器好似一个单一的系统。针对这种情况才有了新的律制，同样的旋律便可以用到其他的音高组织上，而之后的钢琴键盘乐器的出现，便是平均律最好的展现形式。十二平均律贯穿了后续古典主义、浪漫主义以及当代音乐，与我们现在的生活息息相关。这便于我们从听觉心理上对音高“准”与“不准”有了一个平衡判断的标准。同样，从纵向角度看，“和声”是由不同音高在同一时刻有组织地同时发出，从而形成可辨识的音色，当代电子音乐从声音的本质出发，一切皆以复合波中谐波和基波的组合而产生各种不同可能性的音色形态。

而作为二十世纪先锋作曲家，施托克豪森在电子音乐的创作中展现了多元化的创作观念和技术手段。从横向的音高频率组织到纵向“和声化”的音色重塑，从传统的视角到新维度平衡构建，在其不同的创作时期融合了不同风格，形成了新式思维的创作构想。施托克豪森于1954年创作的《STUDIE II》，便能够体现出音乐最基本的音高组织，音色构建的新式维度思考。

一、十二平均律与非平均律

“十二平均律”指在一个八度之内的等比音程频率，均等分12份，每个音与音之间叫一个半音，简称“平均律”，同时也叫十二等比律制。此时的均等分12份，并不是作以除法计算，而以指数函数计算。在键盘乐器上十二平均律的应用，每个八度的倍频程为2∶1，所以两个半音频率比为，因此波长比和音程比就有了以下的对照关系：

波长比例为2：1时，频率比为2∶1，此时呈现了八度的音程关系；

波长比例为3∶2时，频率比为3∶2，此时呈现纯五度的音程关系；

（以小字一组a为例，频率相差2Hz）

波长比例为5∶4时，频率比为5∶4，此时呈现大三度的音程关系。

（以小字一组a为例，频率相差108Hz）

设想，对于十二平均律以两个半音频率比为来计算的话，被开方数“2”作为每个倍频程比例为2∶1，放在国际音高频率对照表里，a1≈440HZ，那么a2≈880HZ；而“12”作为根指数意为在每个倍频程2∶1的规则下平均分成12份，那么也就有我们十二平均律最为详细的定义，在每个倍频程里以2∶1的规则，被开方12份；也就是每个八度之比为2∶1，一个八度里有12个半音。十二平均律被称以“平均律”，那从音高体系里均以“平均律”来运算，即作为所有音高的奠定基础，那么施托克豪森电子音乐作品《STUDIE II》中的“音高”定义皆“非平均律”来作为其音阶模型，作为动机细胞来发展。施托克豪森的作品对于“音高”的定义并非在我们传统的平均律乐器里，而是采用了在20世纪纯模拟时代下压控振荡器（VCO）来作为一个个的发音单元，与传统的平均律乐器不同的是，该单元发声器可以输出任意频率下的纯音（正弦波）信号，而施托克豪森在这首乐曲中采用的非平均律音阶模型，运用81个正弦波，从100Hz到17200Hz不等，以作为每个正弦波之间的恒定比，相比平均律的每个音级恒定比差10%。

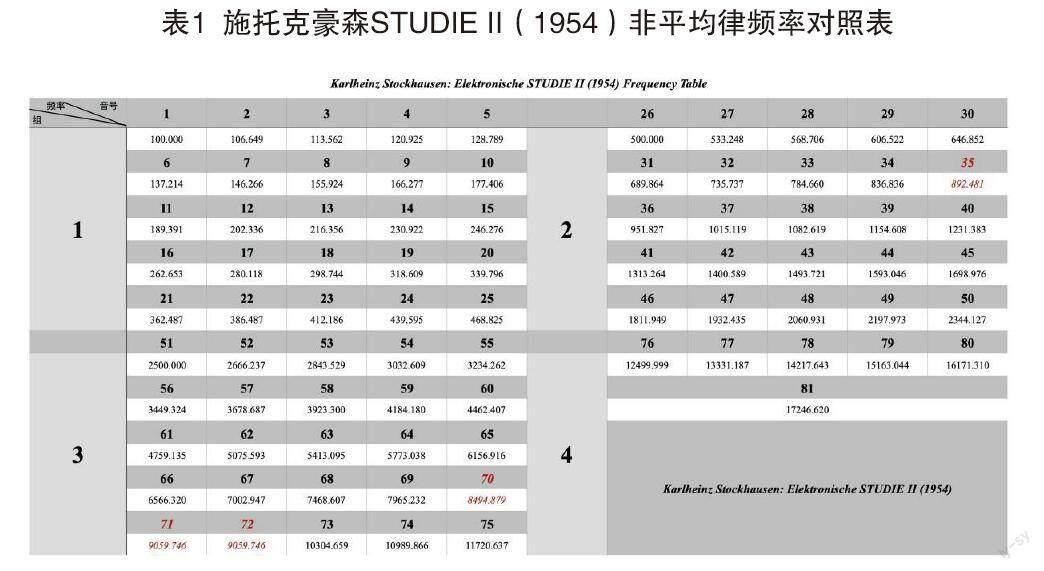
在这首乐曲中，施托克豪森将频率四舍五入到最接近的整数，但是值得注意的是，直到第35号音在893Hz出现了一些差异，第35号音或许是作曲家唯一一个计算错误或者是四舍五入到893Hz上面的，而并非到892Hz，同样在70-72号音也有缺失，这就对于施托克豪森在计算非平均律数值上略有降低偏差（见表1）。

二、非平均律音阶模型构建

施托克豪森在计算得出100Hz—17200Hz下81个非平均律音高之后，他将81个音高进行逻辑化的结构重组，使用以“5”为单位的音高组织模型，将5个不同频率的正弦波进行重叠式组合，组建一个纵向和声式的音阶框架模型，采用了偏移算法将其一一构建。

第一阶音阶模型施托克豪森使用的频率范围在100Hz到2200Hz之间，使用偏移算法，按照音阶的顺序，将五个频率进行分组，构建模型，因此得到了九组包含五个正弦波的音阶模型组合，分别以“100，107，114，121，129；138，147，157，167，178；190，203，217，231，246……”依次按照音高对照表构建五音模型。在一类音阶模型里，一共记有45组，全曲共193组。

同样按照第二类音阶模型，施托克豪森创建了一组新的音阶顺序，这一组通过逐一跳过非平均律音阶的一个频率，然后将这些跳过的频率进行偏移重组，因此在二类的音阶模型里，第一组也跳过了原非平均律里的107Hz与121Hz等，分别以“100，144，129，147，167；217，246，280，318；362，412，469，533，607……”依次类推。所以，所得到的音阶模型被不断扩充延展，一共记有45组，全曲共193组[1]。

在第三类音阶模型中，施托克豪森采用了逐一跳过两个音级，进一步扩大了纵向音阶模型的距离，同样再次从100Hz开始，第一个跳过的频率融合在下一级音阶模型中，同样在这一类的音阶模型里，跳过了107Hz，114Hz，129Hz等，分别以“100，121，147，178，217；263，318，386，469，569；690，837，1015，1231，1401……”依此类推。第三类音阶模型一共有45组，全曲共193组。

第四类音阶模型，施托克豪森继续采用偏移算法，进一步扩大纵向音级距离，逐一跳过两个音级来排列，同样是从100Hz开始，分别以“100，129，167，217，280；362，469，607，785，1015；1313，1699，2844，3679……”依此类推。从第四类音阶模型跳过两个音级来算，纵向“和声化”的听感和之前略有所区别，纵向“和声化”听感音色结构略微稀疏。第四类音阶模型一共有45组，全曲共193组。

第五类音阶模型同样运用偏移算法，不过第五类跳过的频率不再被下一组进行模型重新组建。只有被选定的频率才会进行重组，此类音阶模型类似“五度相生律”算法，将五个选定的频率进行分组，然后重复到下一组，分别以“100，138，190，263，500；690，952，1310，1810；2500，3450，4760，6570，9060……”依此类推。第五类音阶模型一共有13组，全曲第一类至第五类分别45，45，45，45，13组，共计193组。

三、非平均律音阶模型下的音色构建

（一）傅里叶分析

19世纪法国数学家约瑟夫·傅里叶（Joseph Fourier）在其著作《分析的数学原理》中首次提出了傅里叶级数的概念，然而这一概念对于模拟时代与数字时代下构建与生成声音有着重要的作用。傅里叶运算，又称傅里叶分析，是一种数学技术，用于将一个复杂的信号或函数分解成一系列简单的正弦和余弦波成分，这些成分被称为频谱。同样，声音是由不同频率的波形组成的，除去正弦波之外的任何声音波形被统称为复合波，复合波是由基波和不同若干谐波组成的。基波是谐波中最低的频率成分，通常对应于信号的最低频率。基波在复合波中具有重要地位，其通常决定了声音的音高或信号的基本频率。谐波分析是音频合成和音乐乐谱分析的重要组成部分，通过控制不同谐波的振幅和相位可以合成不同音色的声音[2]。

（二）加法合成

任何声音的构建和生成都是可以看作若干频率不同、相位不同、振幅不同的正弦波组合，加法合成是一种用于生成复杂波形的技术，它是基于将多个不同频率的正弦波相加以创建新的波形。加法合成的原理源自上述提到的傅里叶分析，有些时候加法合成也会被叫作傅里叶合成（Fourier Synthesis）。加法合成在声音合成、信号构建技术上属于较早的技术，但是在早期模拟时代，加法合成需要大量的振荡器来实现音色纵向化的构建，从技术手段的实现，到大量振荡器成本上的运用，所以较为难以实现。但是在当今数字时代下，电子管算力到晶体管算力的更新迭代，计算机的优势得以展现。所以该技术在当今数字时代才得以展现其独特的优势。

（三）STUDIE II非平均律音阶模型音色实现

施托克豪森的这首作品采用公式，算得的音阶作为每个正弦波的频率实现加法合成，将每组音阶模型纵向“和声化”音色构建。施托克豪森将5个音作为一组，以此来实现音色的重塑。虽然每个频率都来自公式运算，但是在每组模型里垂直频率范围呈现指数增长。

在数字系统中，通过对每个音阶模型实现音色重塑，将所有五个频率为基波的音阶模型按照顺序进行循环播放，并且对每个声音进行了混响处理，以数字的方式实现了这些选定的音阶模型组合，如#89、#94、#99、#104、#25，代表了不同序列下音阶模型的组合顺序。以下对#89与#25做了和声重塑与原曲声音频谱分析。

第89号音阶模型在全曲第25秒处得以实现，并且在基于Max/MSP环境下“Additive Synthesis Patch”中得以实现音阶模型音色重塑，在该组建中，设定基波为362Hz，依次输入第二号到第五号振荡器剩余89号音阶模型的频率最终得以实现，通过不同维度的声音数据可视化，最后得以还原原曲的音阶模型音色。第25号音阶模型在全曲第1分24秒处得以实现，在该组建中，设定基波为362Hz，依次输入第二号到第五号振荡器剩余25号音阶模型的频率最终得以实现，还原原曲的音阶模型音色，因此，不同的音阶模型所反映出来的频谱结构也是大有区别的[3]。

（四）STUDIE II结构分析

施托克豪森的这首曲子的纵向音阶模型与横向结构都可以数字“5”来解释，从宏观的整个曲子结构到微观的音阶模型，声音合成都离不开“5”。早在理查德·途谱（Richard Toop）对这首曲子的草图图表框架研究中，作品的每个乐段都由5个部分组成，然而每个乐段都由5个乐句组成，每个乐句都由1-5个音阶模型组成，每一个模型都由5个音组成。但在这首作品中，也会存在一些例外。在整个乐曲的宏观结构中，也并非所有的微观组成都是数字“5”，部分微观音色结构包含6个纯波，并非局限于5个，施托克豪森的这种非一致性或许与这部作品独一无二的电子乐谱呈现形式有关，通过对乐曲频谱图分析得以发现，斯托克豪森生成了总共193组非平均律音高频率并将其逻辑化音阶模型有机组合，但并不是所有193个音高频率都被使用，但在整首作品中，100Hz至17200Hz之间的所有频率都曾被播放，或者通过谐波被激发，或包含在其他音阶模型之中。例如，音阶模型第43、44和45号包含频率386Hz等。

四、结束语

《Studie II》非平均律下的音阶模型从传统的十二平均律脱离开，十二平均律可以被视为音乐的本体论表达，它基于音的存在和实体属性，将音乐看作一种客观实体。这引发了关于音乐的本质是什么以及音乐存在的形而上学问题。非平均律则挑战了这一本体论观点，因为它将音的属性视为相对的，可以随意改变，非平均律下的音阶模型是对传统音乐结构的突破，也同时引发了关于音乐实体的多元性和主观性的讨论。

音乐的平均律选择涉及审美标准。十二平均律的规则性和可预测性可能会被认为是符合传统审美标准的，而非平均律可能会引发对审美多样性和相對性的讨论。人在长期的非平均律听感下，再回头听十二平均律，也会注意到音准是否准确的问题，这牵涉到审美哲学的问题，即如何评价音乐的美和音乐审美标准是否普遍适用。

参考文献：

[1]钱仁平，马琳.中国新音乐：人工调式的理论与实践[J].音乐艺术（上海音乐学院学报），2019（01）：90-103+5.

[2]谢嘉幸，张烁.十二平均律音高探索的“终结”？——谈“音级集合”理论的贡献与局限[J].北方音乐，2023（03）：70-75.

[3]陈倩.论人工调式的运用与发展[D].天津音乐学院，2012.