线性再生散度模型的极大Lq-似然估计的渐近性质
2023-12-28胡宏昌吴乔艳
胡宏昌,吴乔艳
(湖北师范大学 数学与统计学院,湖北 黄石 435002)
0 引言
自Jorgensen[1](1997)在其专著中定义了再生散度模型(RDM),并且提出广义线性模型的理论可以推广到以RDM为随机误差的模型之后,唐年胜等[2~4]从2000年开始研究非线性再生散度模型(NRDM)的相关性质,并于2006年在Fahrmeir和Kaufmann[5]的基础上将广义线性模型的极大似然估计(MLE)结果推广到线性再生散度模型(LRDM),得到了该模型MLE的相合性和渐近正态性。Ferrari和Yang[6](2010)研究了基于非广义熵的极大Lq-似然估计(MLqE),得到了指数分布族MLqE的弱相合性和渐近正态性,并通过 Monte Carlo模拟得到:对于中小样本量来说,MLqE比MLE有更好的稳健效果。近年来,不少学者也研究各种模型的MLqE的各种性质,如:极大Lq-似然估计的稳健性[7],Gamma分布的极大Lq似然估计[8],Marshall-Olkin拓展伯尔分布的极大Lq-似然估计[9]。然而,到目前为止还没有学者研究RDLM的MLqE,本文基于Fahrmeir和Kaufmann[10]提出的条件,得到了 RDLM的MLqE的相合性和渐近正态性,通过模拟算例得到:随着n的增大,参数估计值越接近参数真值。
1 预备知识及其假设条件
记yi为响应变量的观测值,xi=(xi1,xi2,…,xim)T为第i个解释变量观测的向量,如果
1)存在一个严格可微的函数g(联系函数),使得
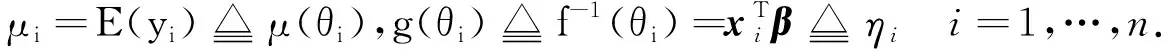
(1)
2)y1,y2,…,yn相互独立,且随机变量yi的概率密度函数为
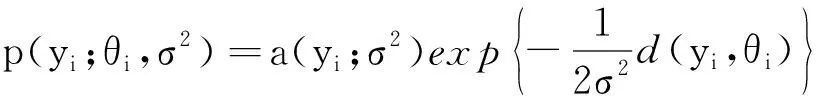
(2)
其中θi=θi(β),β=(β1,β2,…,βm)T(m 由文献[7]可知,线性再生散度模型的极大Lq似然函数为 (3) 为了研究β的相关性质,我们需要如下假设: 假设条件A: i)对∀xi∈χ⊆Rm,χ为定义在Rm上的紧子集,∀β∈B⊆Rm, B为定义在Rm上的凸紧集; iii)β为B的未知真参数,且β0为B的内点; iv)f为二次连续可微函数且f的一阶、二阶导数均有界,df/dη≠0; v)d(y;θ)关于θ是可微的,对∀θi∈Θ,i=1,2,…,n有0 0 vi)qn为一序列,且qn→1(n→∞). 假设条件B: 在证明定理之前,先不加证明地给出一些引理。 引理1[11]令Ψn是一个随机向量值函数,Ψ为一固定的向量值函数,若对∀ε>0满足 (4) 其中 因此,为了证明定理1,我们只需要去证明:对于任意的β∈B,Ψn(β)依概率收敛到Ψ(β). 显然 (5) 则 (6) 下面只需要证明 (7) 注意到 且由条件A(i)(iv)(v)得 其中C为有限常数,全文不同处的C表示不同值。 (8) 因此由式(7),式(8)可知我们只需证明如下式(9)成立即可。 由于 故若证明式(10)成立,只需要证明如下式(11)及式(12)成立即可。 由a(yi;σ2)有界知 对于r=1,2,有 (13) 由于β0为内点,当条件A(vi)成立时,由控制定理可知 于是当n→∞时,有 (14) (15) 定理2 如果假设条件A(i)~(iii)和B成立,则 (16) 其中 (17) (19) 从而由Lindeberg-Levy中心极限定理有 (20) (21) 故 (22) (23) (24) 本节采用I型极值分布来进行模拟,其密度函数为 由表1及表2可以得到以下结论: 表1 β在不同n下MLE的结果 表2 β在不同n下MLqE的结果 1)当q越趋近于1时,极大Lq-似然估计的参数估计值越接近于极大似然估计; 2)随着n的增大,参数估计值越接近于真值,均方误差也越小; 3)当q<1时,极大Lq-似然估计参数的均方误差大于极大似然估计的均方误差;当q>1时,极大Lq-似然估计参数的均方误差小于极大似然估计的均方误差。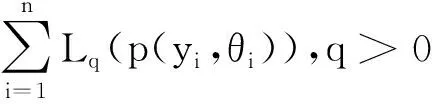
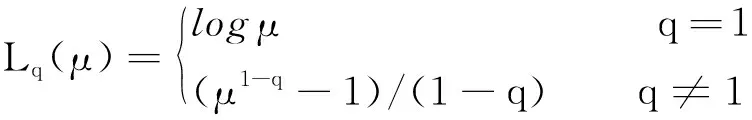
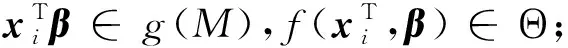


2 相合性和渐近正态性


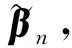
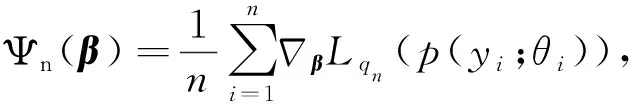

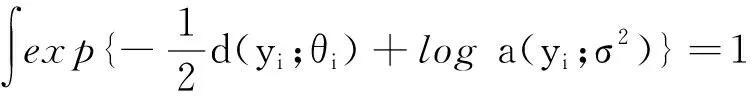

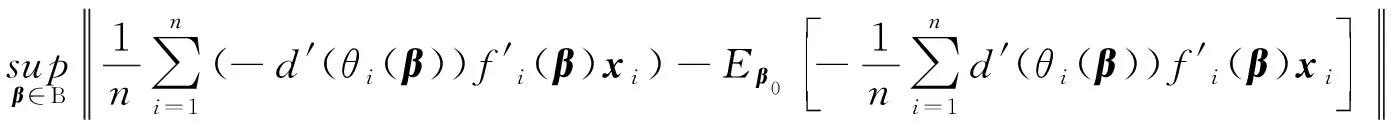
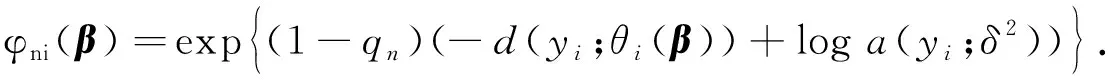
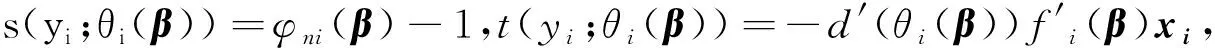
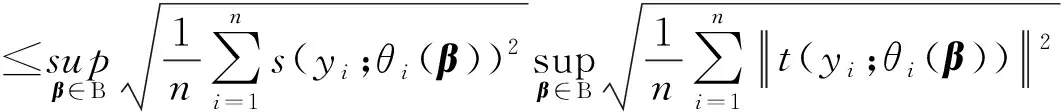

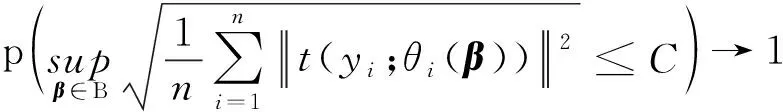
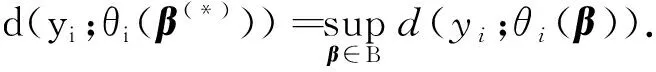

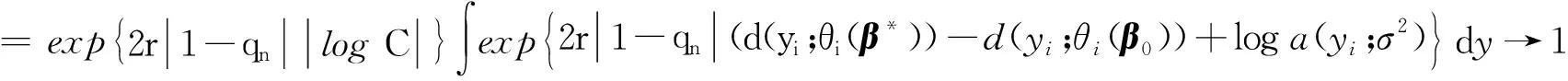
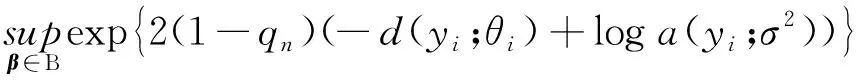
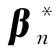

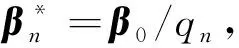
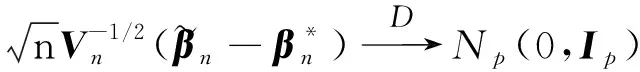
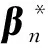
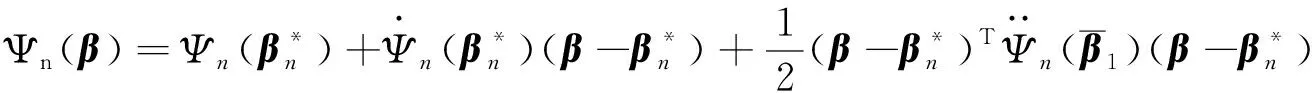
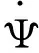
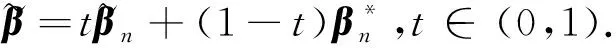

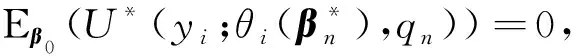

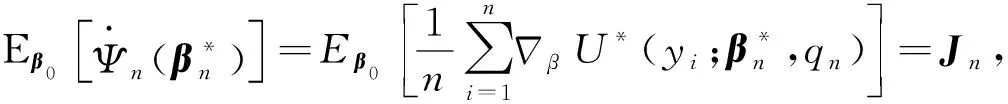
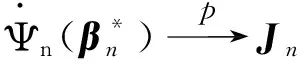


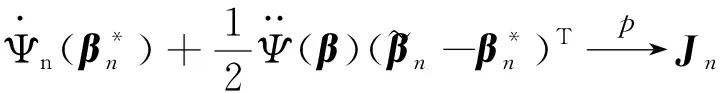

3 模拟算例