融合超像素和多属性形态学轮廓方法的高光谱图像分类

2023-12-28李雷孙希延纪元法付文涛

自然资源遥感 2023年4期

李雷, 孙希延, 纪元法 , 付文涛

(1.桂林电子科技大学精密导航技术及应用广西重点实验室,桂林 541004; 2.桂林电子科技大学信息与通信学院,桂林 541004; 3.卫星导航定位与位置服务国家地方联合工程研究中心,桂林 541004)

0 引言

高光谱传感器集成了传感技术和光谱技术,采集的图像包含几十到几百个波段,具有很高的光谱分辨率,能够从不同角度反映地物的材料特性[1],因此在资源勘探[2]、目标检测[3-5]、土地分类[6]等众多领域都有广泛应用[7],然而,由于成像光谱仪距离地面较远,加上大气传输过程中的多次散射以及表面微观物质的复杂分布,因此在高光谱图像(hyperspectral image,HSI)中经常出现混合像素,即一个图像像素可能覆盖几种不同的物质,因此其分类技术也是众多学者研究的重点。

由于HSI的丰富的光谱特性,在以往的分类方法中,产生了众多光谱信息的特征提取和分类方法,基于光谱信息的稀疏表示方法[8],寻找最优超平面的支持向量机(support vector machine,SVM)分类后处理方法[9],此外,空间信息同样不可忽视,在发现仅使用光谱信息的分类效率有限时,针对空间特征提取的HSI分类方法也被提出,例如利用扩展多属性轮廓(extended multi-attribute profile,EMAP)方法提取空间纹理信息[10-11]。Liao等[12]利用双边滤波提取HSI中的空间信息; Feng等[13]叠加了从原始图像中提取的EMAP和Gabor空间信息,构建HSI单个场景的多视图数据集。

一般来说,上述所提方法皆是从像素级层面对HSI进行信息提取,即直接对HSI进行纹理、光谱等特征提取,除此之外,HSI的另外一种表征方式是超像素分割,其考虑到了空间邻域弱假设,从超像素级层面对HSI进行表征,提高了对HSI的辨识度。Ren等[14]利用超像素改进了异常检测算法RX的自适应内窗; Sellars等[15]采用超像素生成收缩加权图表示,加速了HSI的图形分类器; Jiang等[16]通过多尺度超像素方法与传统的主成分分析(principal component analysis,PCA)方法相结合来学习HSI固有的低维特征,提出了SuperPCA方法; Zhang等[17]改进了SuperPCA方法,将全局PCA方法结合了局部PCA,重建降维HSI; Beirami等[18]采用波段分组技术改进了SuperPCA方法,总体精度比传统SuperPCA提高了8百分点; Jia等[19]建立了超像素之间的相似度矩阵,在超像素特征层面传播样本标签。

但是上述方法均建立在超像素分割方法能够完全提取信息的基础上,其他处理方案诸如波段分组、线性判别分析(linear discriminant analysis,LDA)、PCA等只是辅助,因此分类的结果极度依赖分割方法的参数设置。本文受SuperPCA方法的启发,从超像素方面来表示HSI,然而,并没有一种最佳的方式能够完整无缺地利用HSI的丰富信息,同样地,也没有任何单独的一种表达方式能够完整地表达HSI,性能较好的超像素分割方法也是比较依赖参数设置,需要进行多次重复实验才能取得令人满意的效果。因此,本文介绍了一种HSI分类方法,重点在于解决超像素分割方法依赖参数严重以及单一方法提取信息不充分的问题。该方法建立在超像素分割方法基础上,分别从超像素级和像素级层面提取HSI特征并相结合。采用熵率超像素分割方法(entropy rate superpixel segmentation,ERS)将HSI分割为一个个单独的区域,然后对每一个同质区域进行PCA分析,并重新组合,提取了HSI的低维固有的局部特征; 采用EMAP方法提取纹理特征,之后将2种信息进行融合,并采用递归滤波(recursive filtering,RF)方法去除信息融合后的冗余,最后进行分类。该方法将提高分类精度,减少对超像素数目设置的依赖性,提高单一方法对HSI的信息提取程度。

1 理论模型

本文提出的分类框架如图1所示,主要包括4个主要部分: ①超像素级特征生成; ②生成EMAP特征; ③分别融合这些特征并采用RF方法滤波; ④进行SVM分类,确定最后的分类标签。

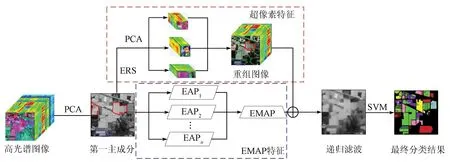
图1 分类框架示意图

1.1 超像素级特征生成

超像素分割方法基于相邻像素具有相似结构的假设,将整个图像精细划分为多个彼此不重叠的同质子区域,小尺度分割的超像素在强度上和纹理特征上都具有较高的一致性,由于其简单、高效和鲁棒性,被广泛应用于图像处理的预处理过程。由于原始的HSI波段众多,因此分割之前需要对HSI进行PCA处理,获得贡献率最大的第一主成分If,然后使用ERS对图像的第一主成分进行分割[11],描述为:

(1)

式中:Yk和Yg分别为互不重叠的同质区域;S为总的超像素数目。

传统的降维方法多是在全局层面对整个HSI进行PCA分析,忽视了HSI的局部特征。受到SuperPCA方法[16]的启发,为了提高对HSI的信息挖掘程度,本文采用一种“分而治之”的策略: 在生成同质区域后,对每一个同质区域进行单独的PCA分析,然后再将它们组合起来形成新的降维HSI,如图2所示。图2中首先将超像素分割后的图像作为目标处理图像,可见图像被划分为多个均匀区域,每个区域由矩阵表示,矩阵列为像素的谱向量,B为原始的波段数,Si,Sj和Sk是均匀区域的位置标识,将PCA应用到每个区域中,使波段数目由B减少到d,按照原来的位置重新组合Si,Sj和Sk,即可得到新的特征集合Hsp。

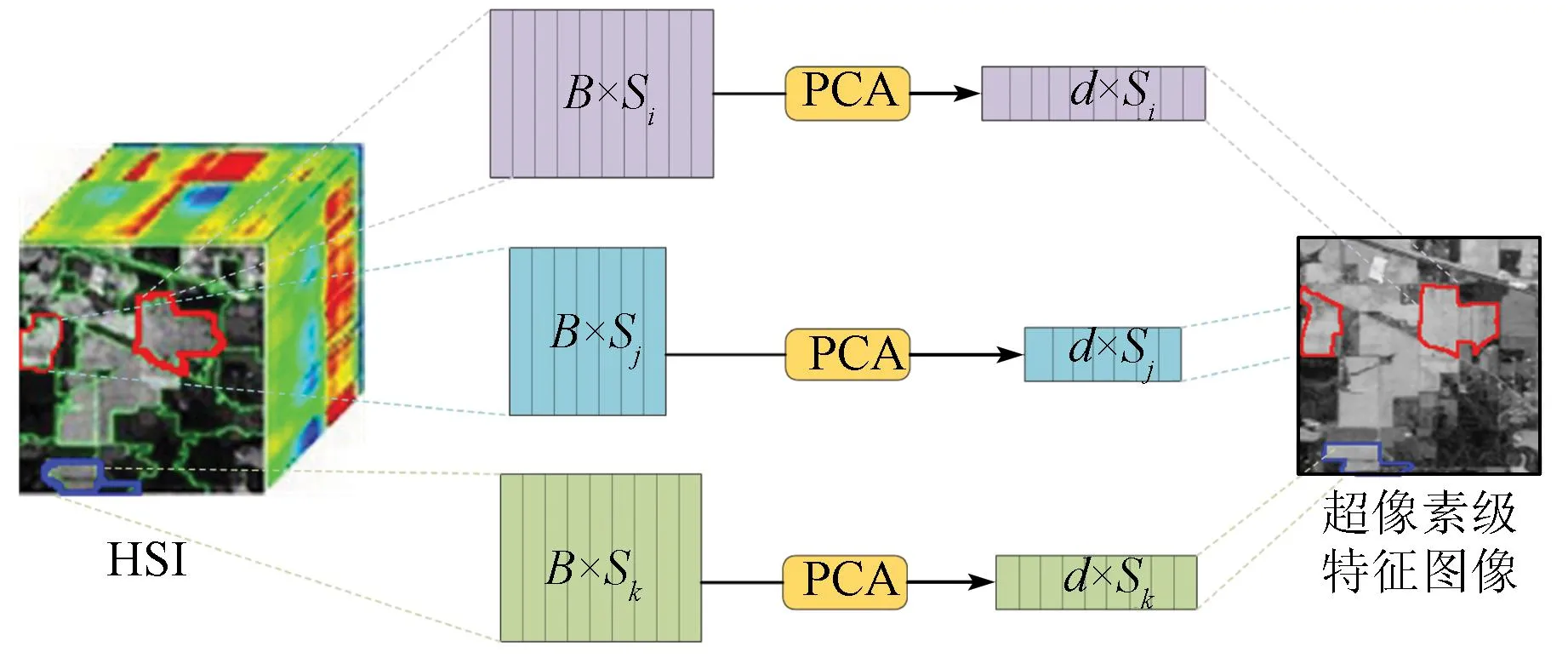
图2 获取超像素级特征

相对于全局意义上的PCA分析,针对每一个同质区域进行PCA固然是增加了计算量,但由于PCA的高效性,两者的计算量差距可以忽略不计。而带来的好处是可以显著提高第一特征向量方向的偏心率,即有效在低维空间中保存基本数据信息,经过重组后的图像Hsp视为超像素的特征图像。

1.2 像素级特征生成及融合

像素级特征的提取采用EMAP方法,作为传统形态学剖面纹理特征提取方法的改进,EMAP级联了多种属性原则的形态学滤波器[20],其做法是首先对HSI进行PCA分析,然后根据面积、标准差、形状等准则,分别生成不同的属性文件(attribute profile,AP),然后级联起来形成扩展属性文件(extended attribute profile ,EAP),公式为:

EAP={AP1,AP2,…,APn}

(2)

式中:APi(i=1,2,…,n)为对分量i的属性滤波;n为主成分个数。EMAP是将不同属性特性向量级联成单一向量(图3),公式为:

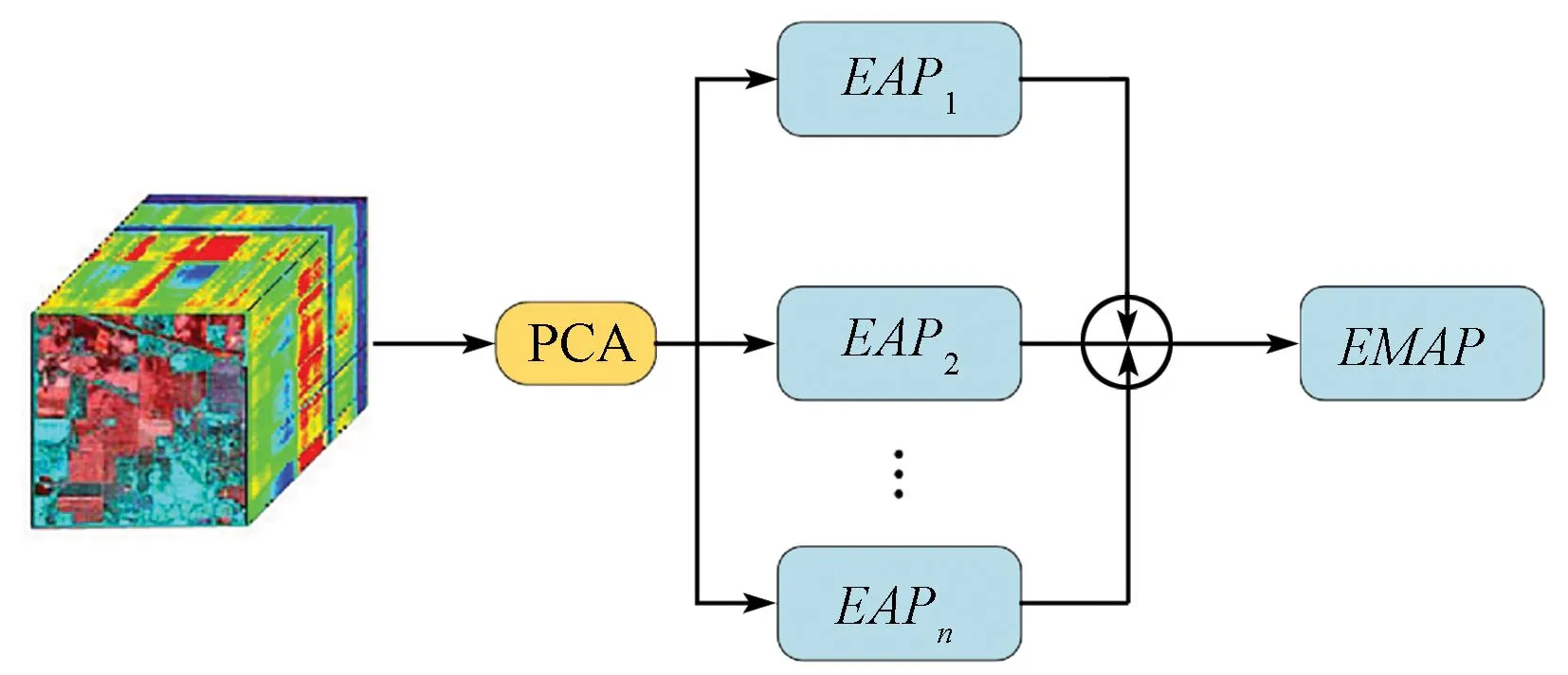
图3 获取像素级特征

(3)

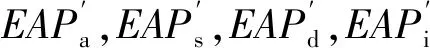
EMAP方法的像素级特征提取采用阈值参数计算,该参数相当于单个特征的平均值为2.5%～10%,标准偏差为2.5%,面积属性为200和500的阈值,由于EMAP特征生成要增加众多的维度,因此本文基于HSI的前3个主成分分量生成EMAP特征HEMAP。

1.3 融合特征及分类

EMAP方法集中考虑了图像的全局特征,基于超像素级的分割方法生成的特征Hsp是基于局部的PCA来学习固有的低维特征,这2种特征形成了信息互补,重要的是,EMAP特征弥补了分割方法提取边缘信息的不足的缺陷。因此采用一种简单的融合方法,将2种特征沿着光谱维度叠加起来,计算公式为:

H=[Hsp,HEMAP]∈R

。

(4)

在分类之前,由于融合了多个特征,新特征的维度会变大,因此需要对新的特征再次进行PCA分析,提取HSI的光谱-空间特征,方法是对融合后的图像进行域变换RF, 获得特征图像,公式为:

O=RF(H)δs,δr

(5)

式中:RF为域变换递归滤波操作;δr和δs分别为空间和范围标准差参数;O为产生的特征图像。

最后,采用SVM分类器来获得最后的分类标签图label,其中,分类器的核函数选用高斯核函数(radial basis function,RBF)。

label=SVM(O)RBF

。

(6)

2 实验及分析

为了验证所提方法的可行性和有效性,本文选择2个数据集作为试验场景,同时以SVM,PCA,LDA ,SuperPCA[16], S3-PCA[17],BG-SuperPCA[18]几种方法作为对照试验,均在一台2.5 GHz CPU和12 GB 内存的笔记本电脑上使用MATLAB进行实验,同时为了评估总体分类性能,使用3种常用的分类指标,即总体精度(overall accuracy,OA)、平均精度(average accuracy,AA)和Kappa系数。OA是正确分类的像素的比例,AA是每个类别中正确分类的特征的比例,Kappa系数则基于混淆矩阵,综合了OA和AA这2种精度指标,取值越靠近1,表明其分类效果越好,其中,Kappa系数是图像分类精度的最有价值的评价指标[21]。

2.1 实验数据集

实验选择2个经典的高光谱数据集: Indian Pines数据集和University of Pavia数据集[22]。

Indian Pines数据集是位于美国印第安纳州西北部的印第安松树试验场景。该场景尺寸为145像元×145像元,空间分辨率为20 m[22]。该图像删除了20个多余的吸水波段,共包含220个波段,并包含16种地物。真实地物图以及伪彩色图如图4所示。University of Pavia数据集为拍摄于意大利帕维亚大学周围的城区场景,尺寸为610像元×340像元,空间分辨率为1.3 m,为了消除噪声影响,将原始拍摄图像制作成数据集时,去除了被冗余的被水体吸收的波段,共115个波段[22]。图5 显示了图像的波段合成图,以及真实的特征图。

(a) 伪彩色图 (b) 地面标记样本

2.2 数据集实验

对于2个数据集,随机从样本总含量中选择10%标记样本作为训练样本,剩余的作为测试样本。RF的参数分别为δs=200,δr=0.3; SVM分类器采用RBF核,参数选择默认的参数; 超像素数目设置为S=100。每个数据均重复10次取平均值为最后结果。

2.2.1 Indian Pines 数据集测试

图6所示为几种对照算法和本文算法在Indian Pines数据集的分类结果,从图6(b)中可以看出SVM方法错分、误分类现象严重,出现了很多的噪点,说明了在本文算法中进行滤波处理的必要性,其好处是在减少数据量的同时,也降低了误分类现象出现的概率,本文算法中的分类结果(图6(h))中误分类的情况大大减少,整体分类效果优于其他同类算法。

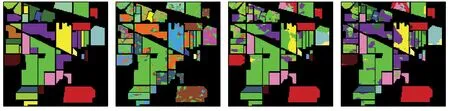
(a) 地面真值 (b) SVM (c) PCA (d) LDA

表1中给出了6种对照算法分别在3种分类精度评价指标上的数据对比,其中,PCA和LDA方法仅仅提取了光谱信息,因此在分类精度有限,S3-PCA由于是在SuperPCA方法的基础上提取了全局特征,因此精度有所提升。BG-superPCA方法是在superPCA基础上将初始图像的波段进行分组,原因是考虑到相邻波段之间拥有相似的信息,聚合波段在一定程度上减少了冗余小噪声的干扰,但其精度依赖超像素数目,随机超像素数目下表现略差。本文提出的方法在增加了纹理特征的同时,采用RF方法去除了细小的噪声,因此在3个精度评价指标上较其他算法均有明显提升。其中,Kappa系数较最高的S3-PCA方法提高了3.55百分点,AA提高了2.24百分点。

表1 Indian Pines 数据集分类精度对比

2.2.2 University of Pavia数据集测试

图7为在University of Pavia数据集中的实验分布结果,可以看到虽然该数据集包含的细节较多,本文提出算法的分类精度仍优于其他算法,这是因为与其他方法相比,本文算法综合考虑了HSI中固有的低维特征,使用EMAP方法保留了边缘地物的轮廓细节信息,对比算法中的各个分类精度也在表2中给出。由表2可见,本文方法在此数据集中在3种分类评价指标上依然保持优势,Kappa系数较SVM方法提高了14.23百分点。

表2 University of Pavia 数据集分类精度对比

(a) truth (b) SVM (c) PCA (d) LDA

2.3 参数变化对比

本节实验测试不同训练集比例对3种分类精度的影响,测试分别在2个数据集上进行,数据集比例分别设置从5%～40%,间隔5百分点,测试3个分类精度的变化。图8为在2个数据集中,3种分类精度随训练集比例增加的变化图。当训练集比例均从1%逐渐增加至40%时,3种分类精度均在提高,验证了本文方法的有效性。

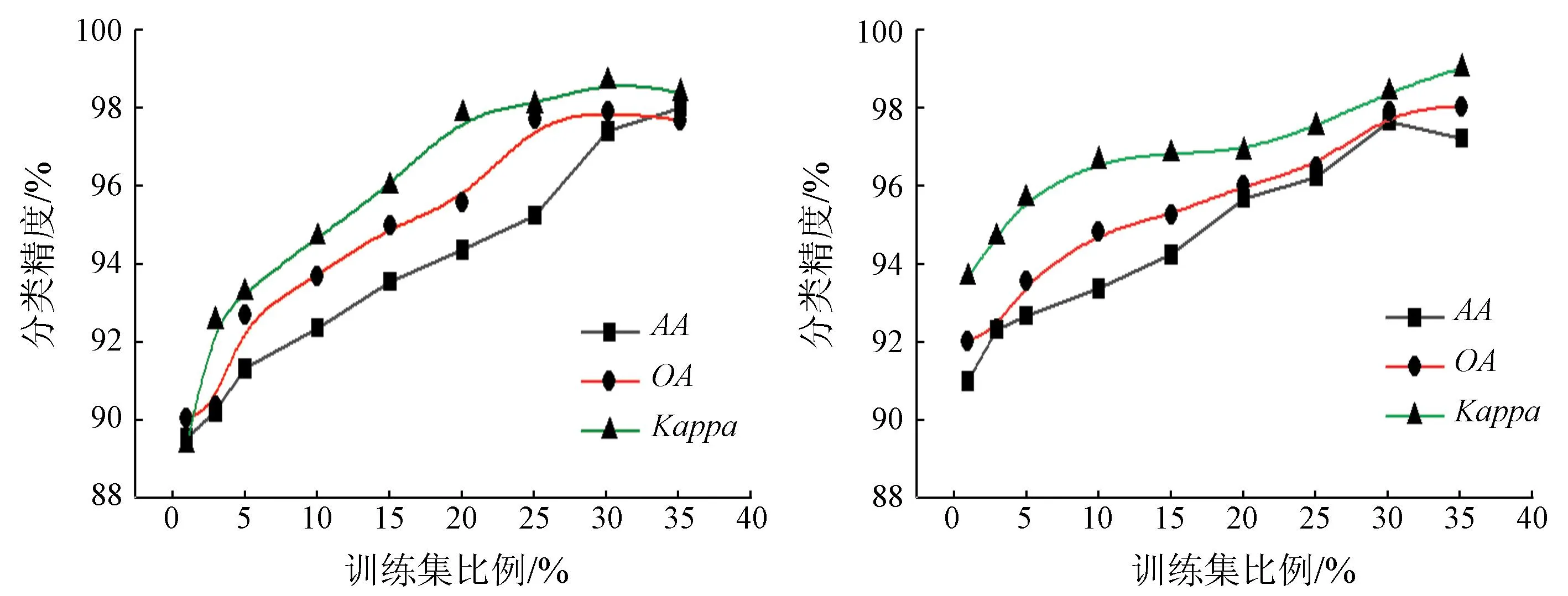
(a) Indian Pines (b) University of Pavia

图9为在2个数据集中,以10%训练集,进行测试Kappa系数随超像素的数目变化,可以看出,超像素数目的增加会对Kappa系数造成一定的影响,即有轻微的下降趋势,但总体来看,在超像素数目很高时,2个数据集中的Kappa系数依然有令人满意的表现,这是因为EMAP方法弥补了由于超像素过高导致图像过分解时的缺陷,说明了本文算法能够很好地减少对超像素参数的依赖性。

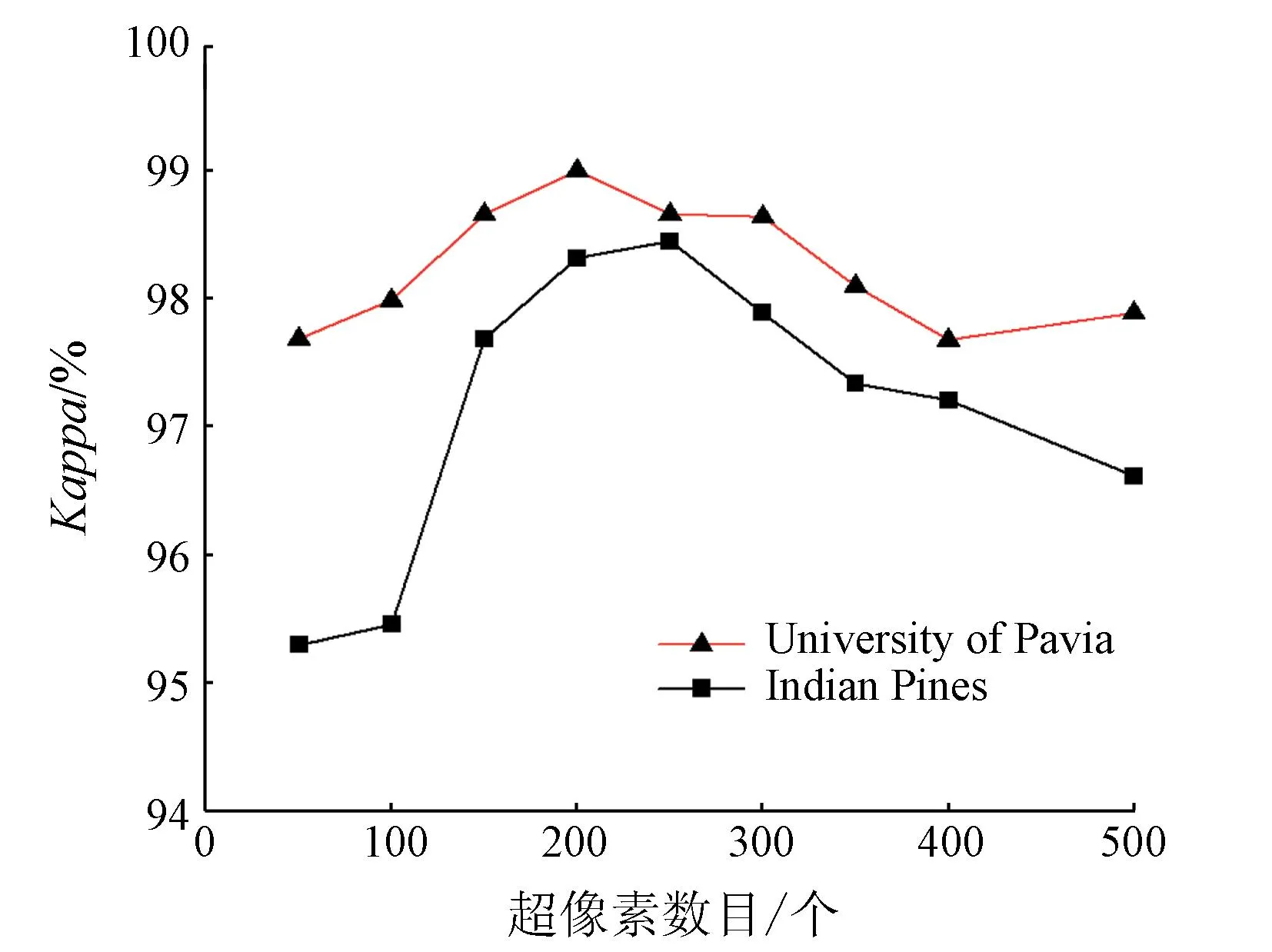
图9 Kappa系数随超像素数目变化图

2.4 消融实验分析

为了全方位验证本文方法的有效性,在本节中,分别在Indian Pines数据集中将EMAP特征、光谱学RF、超像素特征这3种步骤去除,将训练集逐渐增加至40%,观察Kappa精度的变化,来测试每一个步骤的必要性。

图10可以看出,当去掉超像素特征时获得的Kappa精度最低,精度较完整方法下降了约10百分点,可见对高光谱图像进行局部特征提取的必要性。不叠加EMAP特征时获得较高的精度,去掉RF步骤的效果次之。但是均未达到完整方法的效果,验证了叠加EMAP特征为提取纹理特征时起到了积极的效果。综合来看,去掉任何一个步骤时,都不能达到完整算法所达到的效果,本文提出算法的每一个步骤均对特征提取过程起到了积极作用,每一个步骤都缺一不可。