基于BEPS-Terrainlab V2.0模型的鄂西犟河流域NPP模拟及环境响应分析
2023-12-28陈佩佩张利华崔越陈俊宏
陈佩佩, 张利华, 崔越, 陈俊宏
(中国地质大学(武汉)地理与信息工程学院,武汉 430074)
0 引言
植被净初级生产力(net primary productivity, NPP)是指在单位时间、单位面积内,植被通过光合作用得到的全部有机物去除植物呼吸消耗能量后的剩余部分[1],NPP不仅在碳循环中发挥着无可代替的作用,同时在生态系统中也扮演着不可或缺的角色[2],很多国际研究项目,如“生物圈计划”、“世界气候研究计划”都把它列为研究的中心内容[3]。目前,在环境问题以及碳循环备受关注的同时,研究植被净初级生产力以及其影响因子对减缓全球变暖以及分析区域生态系统循环过程等研究具有重要意义。
获取NPP的方法有很多: 站点实测法、遥感数据产品以及模型模拟等。建立实测站点受研究区域条件影响较大并且只适用于小范围研究区域,人力耗费较大。MODIS 的NPP产品(MOD17A3)目前是广泛被认可和应用的数据产品,但是此产品时间分辨率为1 a,不适合研究较小时间尺度上的NPP情况,且空间分辨率为500 m×500 m,数据缺失像元较多,对于小流域尺度的NPP空间异质性分析适用性不强。随着遥感技术的不断发展,遥感资料覆盖范围广,更新速度快,遥感数据结合生态模型进行NPP的估算成为当前的研究热点之一,例如BEPS-Terrainlab模型[4]、InIEC模型[5]、BIOME-BGC[6]模型等。其中BEPS-Terrainlab模型是BEPS生态模型[7]和Terrainlab分布式水文模型[8]的耦合,是遥感驱动的生态过程模型,在实践运用的过程中形成了不同的版本[9]。BEPS-Terrainlab V2.0在模拟水文循环过程时不仅考虑了地表覆盖、植被结构、土壤特性等地理因素,同时还引入太阳辐射、降水等气候因素对结果的影响; 另外考虑到地形因素以及阴阳叶对生态水文循环的影响,输出数据的空间分辨率为30 m×30 m,以日为时间步长,对于小流域尺度生态水文参数(如NPP,ET等)的时空演变分析更具有适用性。
犟河流域是南水北调水源保护的核心区域,本文在进行模型模拟精度分析的基础上,基于BEPS-Terrainlab V2.0模型对流域1986—2017年NPP的时空分布特征进行模拟,获得流域高分辨率的NPP分布数据,并探讨NPP时空演变特征及其对地形、土地覆盖、气候变化等因子的环境响应,模拟结果对流域植被保护、生态恢复以及碳循环特征等均具有重要的借鉴意义。
1 研究区概况
犟河是堵河的一级支流,河流总长50 km,发源于张家湾区的花果街道,共有大小支流22条,于黄龙镇东湾村处与堵河进行交汇,随堵河一起流入丹江口水库。犟河流域(图1)位于湖北省十堰市城区西部,地理坐标为E110°33′50″~110°42′9″,N32°27′27″~32°42′60″,流域面积326 km2,整体地势西南高、东北低,流域海拔范围为139~1 441 m。流域位于亚热带季风区,降雨以每年6—9月为主,年降雨量800~1 000 m。植被覆盖度较高,森林覆盖范围较广,主要植被类型有暖温带落叶阔叶林、暖温带常绿针叶林、针阔混交林等。
2 数据与方法
2.1 BEPS-TerrainlabV2.0模型原理
BEPS-TerrainlabV2.0包含冠层辐射传输、碳循环、水循环、生理调节等模块[10],模型输入数据包括高程、坡度坡向、土壤质地、气象、土地覆盖类型、叶面积指数(leaf area index, LAI),空间分辨率为30 m×30 m。模型输出数据包括蒸散发、总初级生产力、净初级生产力、地表径流、地下水位、土壤温度和土壤湿度等生态水文数据,以日为时间步长,空间分辨率与输入数据一致。其在模拟植物光合作用时将植物叶片划分为阳叶和阴叶[11],分别计算阳叶和阴叶的光合过程,利用逐日积分方法在时间上进行了扩展,获得植被的总初级生产力,在扣除植物自身呼吸之后,获得植物的净初级生产力[12]。
1)将冠层分为阳叶与阴叶分别计算植被冠层叶面积指数,公式为:
(1)
,
(2)
式中:LAI为叶面积指数;LAIsun和LAIshade分别为阳叶、阴叶的植被冠层叶面积指数;θ为太阳高度角; Ω为叶片聚集度指数。
2)计算植被冠层总初级生产力GPPcanopy,公式为:
,
(3)
式中:Asun和Ashade分别为阳叶、阴叶的净同化速率( mol·m-2·s-1)。
3)计算NPP,NPP通过GPP扣除植物自养呼吸(Ra)后得到,自养呼吸由生长呼吸(Rg)和维持性呼吸(Rm)2部分组成,公式为:
,
(4)
,
(5)
,
(6)
,
(7)
式中:GPP为总初级生产力;i是指植被的不同组分(1,2,3分别代表叶、茎、根)。
2.2 数据源及其预处理
1)高程数据。数据源自地理空间数据云(http: //www.gscloud.cn/)的SRTM1 DEM数据,空间分辨率为30 m,下载影像行列号为path110/row032。使用ArcGIS软件对DEM数据进行处理,通过水文分析等工具可以获得研究流域边界,同时可以获取研究区域坡度、坡向数据以及裁剪其他数据的掩模。
2)遥感数据。数据源自美国地质调查局官网(http: //glovis.usgs.gov/)的Landsat5-8影像数据,选取生长季(5—9月)影像进行下载,空间分辨率为30 m×30 m,下载影像行列号为path125/row037,2013年前使用Landsat5数据,2013年后使用Landsat8数据。在ENVI中对下载的遥感影像数据进行预处理后使用流域边界数据进行批量裁剪,使用神经网络法进行土地覆盖类型分类,将土地覆盖类型分为阔叶林、水体、城镇、针叶林、混交林、裸地、农田7种,以5 a为间隔进行土地覆盖分类。模型需要输入时间序列LAI,建立常用植被指数(归一化植被指数、比值植被指数、差值植被指数、调整土壤亮度植被指数、大气阻抗植被指数)与野外实测LAI值的回归模型,选取了线性方程中R2最高的反演模型,即RVI与LAI的线性拟合方程,公式为:
LAI=1.073 5RVI-5.321 9
。
(8)
在ENVI中使用波段运算得到RVI,再通过此方程计算LAI 。
3)气象数据。获取到的十堰市气象数据包括1986—2017逐年间日尺度的最高温、最低温、平均气温以及降水。使用Magnus-Tentens近似法将缺少的露点温度补充完整。研究区域所属地级市无太阳辐射数据,使用反距离加权法将研究区域周围4个方向的城市气象站(安康、侯马、南阳、宜昌)的太阳辐射数据进行加权平均,得到的数据来代替研究区域的辐射数据输入模型。
4)土壤数据。野外采集土壤样品,通过马尔文3000高分辨激光粒度仪测量土壤粒度,在ArcGIS中通过克里金插值绘制研究区域内每种粒度的分布图,在ENVI中通过波段运算将砂土、壤质砂土、砂质壤土和粉砂壤土4种不同土壤质地像元分别赋值为10,20,30和40。
2.3 研究方法
2.3.1 一元线性回归分析法
本研究采用一元线性回归分析法逐像元对犟河流域植被净初级生产力在1986—2017年间变化趋势进行分析,计算公式[13]为:
,
(9)
式中:n为时间序列的年份数,应用到本研究中n值取32;i为时间变量,i=1,2,…,n;Ni指第i年的NPP均值;slope为研究因子的变化趋势,slope>0时说明在研究时间范围内NPP值呈增长趋势,slope<0时NPP值呈减少趋势,slope数值的大小表示NPP值增长或减少的幅度。
2.3.2 M-K突变检验
M-K检测可判定时间序列中有无突变,若有,则判定突变发生的时间[14]。通过定义UF,UB这2个统计量来分析样本时间序列的变化趋势,UF>0说明变化趋势持续增长,UF与UB相交于置信区间 [-1.96,1.96]内,说明该交点对应年份的相关数据在变化趋势上产生突变情况。
2.3.3 线性回归分析
线性回归的过程就是把各个自变量和因变量的值建立回归方程后,通过逐步迭代与拟合,找出回归方程式中的各个系数,构造出一个函数式,使用线性回归参数判断自变量和因变量的关系,由于本研究自变量较多,故而使用偏相关系数来进行相关性分析,能够在一定程度上减少自变量直接的相关性对分析结果的影响。
3 结果与分析
3.1 模型精度分析
3.1.1 通量站数据验证
由于研究区域范围内没有建立通量站,于是本次研究获取大九湖盆地的涡度相关系统NPP通量数据,获取的数据时间范围是2016年1月1日—2016年11月21日。大九湖盆地地理位置处于湖北省神农架林区西部,距离研究区130余km,通过临近地区通量站的数据来进行模型模拟精度的检验,绘制实测值和模拟值的变化趋势图见图2。在图2中可以看到模拟值和实测值变化趋势大致相同,且吴宗钒在大九湖区域采用BEPS-TerrainlabV2.0模型模拟NPP值与大九湖实测NPP值拟合R2=0.85[15],可以说明该模型在模拟小流域生态水文过程上具有适用性,模拟结果具有分析价值。

图2 犟河流域模拟NPP与大九湖实测NPP数据对比图
3.1.2 NPP产品数据交叉验证
MODIS的MOD17A3是NPP产品(图3),时间分辨率为1 a,空间分辨率为500 m, MODIS数据在该研究范围内存在较多空白值,且像元数量较少(共有1 471个有值像元),因而MODIS数据在小空间尺度研究上存在局限性。将模型模拟的不同覆盖类型的年总NPP与其他模型模拟的NPP值进行对比,结果如表1。从表中可以看出,模型模拟得到的值略高,但不同植被覆盖类型NPP值的大小关系基本相同。

表1 BEPS-Terrainlab V2.0模型模拟土地覆盖类型NPP数据与其他模拟或实测值对比

图3 MOD17A3数据空间分布
3.2 时间变化规律
3.2.1 时间分析
模型运行输出后得到的是1986—2017年间日尺度的NPP数据,依据不同的时间单位,可以从年尺度和日尺度上2个方面上对NPP进行时间变化的分析。以日为时间尺度,用来描述NPP在一年内的变化,将具体年份的年内变化进行汇总得到NPP年内变化的多年平均值,见图4。

图4 犟河流域NPP年内多年平均变化
可以发现NPP年内多年平均随时间变化的走向呈单峰式变化,先升后降。冬季(1—60天、330—365天)值最低,春季(60—150天)呈上升的趋势,夏季(150—240天)时达到了峰值,也是NPP数值最高的阶段,秋季(240—330天)NPP呈缓慢下降的趋势。从NPP变化的趋势可以看出,在夏季(150—240天)内有突然下降的波动,并且在秋季(240—330天)存在短暂波动较大的情况。
以年为时间尺度,统计1986—2017多年年总NPP,反映多年来研究区域NPP变化的情况,见图5。

图5 犟河流域NPP多年年总变化
由图5可知,年总NPP大体变化趋势为波动上升,最低值出现在1995年,NPP值为911.86 gC·m-2·a-1,最高值出现在2007年,值为1 482.28 gC·m-2·a-1,1986—2017年间NPP的多年平均值为1 232.70 gC·m-2·a-1。
3.2.2 突变检验
使用DSP数据处理系统对多年年总NPP进行M-K检验,结果如图6(a)所示,Uf-UB曲线在置信水平区间内相交于2004年,说明NPP时间序列在99%置信水平下突变于2004年,以2004年为分界点绘制多年年际NPP变化趋势图,如图6(b),可以看到2004年之后NPP的变化幅度明显大于2004年以前,2004年以前,NPP总体变化趋势较为平缓,2004年以后NPP变化趋势明显增大。

(a) M-K检验结果 (b) NPP变化趋势
3.3 空间变化规律
在ENVI中将模型输出的1986—2017年的年总NPP数据进行波段合成,输出研究区域多年平均NPP影像,能够得到研究区域多年平均NPP在空间上的分布,如图7(a)所示,通过一元线性回归分析对1986—2017年NPP数据进行分析,得到这32 a间NPP在空间上的变化趋势值,如图7(b)所示。

(a) 总NPP空间分布图 (b) 空间变化趋势图
多年NPP在空间上分布呈现南高北低的分布,南部最高可达到1 925 gC·m-2·a-1,在主流域附近NPP的值最低,受地势及不同土地覆盖类型的影响,NPP的分布在空间上呈现差异性,图7(b)为1986—2017年NPP值在空间上变化的趋势,在大部分区域NPP值都呈现增加的趋势,在河流区域变化不大。
3.4 环境影响因子分析
3.4.1 土地覆盖因子
研究区域土地覆盖类型分为7类,主要有针叶林、阔叶林、混交林、水体、农田、裸地和城市。由于裸地以及水体植被覆盖度较低且分布面积占比不是很大,于是就其他5类类型数据来分析NPP的分布情况。由图8(a)可见,不同植被覆盖类型的NPP不同: 阔叶>混交>针叶>农田>城市,结果与薛梅在东北地区估算的不同植被类型的NPP大小排序结果相同[19]。其中混交林NPP的值最高,其次针叶林NPP值略高于阔叶林。

(a) 土地覆盖因子 (b) 土壤因子 (c) 高程因子
3.4.2 土壤因子
将研究区NPP分布按照不同土壤质地进行划分,绘制箱线图如图8(b),犟河流域不同土壤类型平均NPP按大小排序为: 砂土(1 363.8 gC·m-2·a-1)>砂质壤土(1 177.1 gC·m-2·a-1)>壤质砂土(1 348.6 gC·m-2·a-1)>粉砂壤土(932.9 gC·m-2·a-1)。
3.4.3 地形因子
将研究区NPP分布按照不同高程进行划分如图8(c),得到年总NPP随高程每增加100 m的变化趋势,NPP随着海拔的上升而增加,在100~900 m呈上升趋势,在高程为900 m时达到最大值而后变化趋势逐渐趋于平稳,这与植被的垂直分布有关,在高程为900~1 300 m时,土地覆盖类型为针叶林和混交林,根据前文中已知混交林和针叶林的NPP值较高于其他土地覆盖类型。
3.4.4 气象因子
影响NPP的变化的气象因素有很多,诸如温度、辐射以及降水等,采用线性回归分析分析来探讨NPP与这些气象因子的相关性,可以进行较长尺度下的气象影响因素的分析。在SPSS中添加因变量年内NPP以及年际NPP数据和自变量气温、降水、辐射、风速、LAI等自变量数据,对这些数据进行线性回归分析,由于自变量间可能存在互相影响,探讨各自变量对于因变量的影响力大小时,选择以偏相关系数大小为判断依据,以标准化回归系数作为参考(表2)。
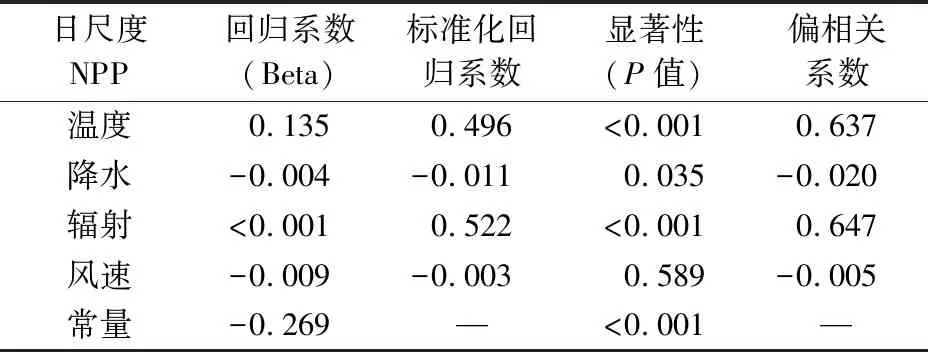
表2 日尺度NPP线性回归方程参数
由表2可以看出,影响力最高的是太阳辐射,偏相关系数为0.647,P值小于0.001,说明辐射与NPP显著性正相关; 其次温度的偏相关系数为0.637,P值小于0.001,具有显著正相关,说明温度对NPP影响也较大。降水与风速的P值较大,与NPP存在弱负相关的关系,对NPP的影响较小(表3)。

表3 年尺度NPP线性回归方程参数
由表3可知,偏相关系数最高的是LAI,P值小于0.001,属于极显著正相关,降水偏相关系数为0.305,影响力有所提升; 温度对年尺度NPP的影响显著降低,其他因素对年尺度NPP的影响都较小,偏相关系数较低且P值较大。
4 结论
本研究基于遥感以及气象等数据结合BEPS-TerrainlabV2.0模型对湖北省十堰市犟河流域1986—2017年NPP进行分析,讨论了其时空分布以及与环境因子的相关性分析,结果表明:
1)与相近地区通量站数据以及MODIS数据进行分析,验证了该模型对于较小空间尺度的适用性,同时与其他数据产品进行交叉验证,证实了模型结果的可用性。
2)犟河流域NPP的年际变化具有波动性,空间上总体分布南高北低,不同植被类型的NPP模拟值为阔叶>混交>针叶>农田>城市; 不同土壤类型NPP值为砂土>砂质壤土>壤质砂土>粉砂壤土,同时NPP值随着海拔的上升而增加,在海拔为900 m以上时,增加的趋势逐渐趋于平缓。
3)日尺度上,气象因素对NPP影响较大,太阳辐射和温度与NPP的偏相关系数达到0.6左右,较长时间尺度上NPP对LAI的反响最强。
同时由于选取区域较小,无通量站观测数据,且目前国内存在的NPP数据产品大多是500 m分辨率,在对模型结果精度验证上有一定的局限性,考虑在后续的实验中进一步改进模型结果的验证准确性。
