地震作用下危岩体倾倒破坏过程的数值模拟
2023-12-28和铁柱邱海燕王基禹孟凡豹刘康琦
和铁柱,邱海燕,王基禹,孟凡豹,刘康琦,3
(1.保利民爆哈密有限公司,新疆 哈密 839200;2.哈密市和翔工贸有限责任公司,新疆 哈密 839200;3.中国地质大学(北京)工程技术学院,北京 100083)
0 引言
在露天矿山开采中,频繁的爆破和开挖作业会对矿山边坡造成强烈的扰动作用,从而产生大量节理裂隙发育的危岩体,危岩体的存在会对矿山开采工作产生严重影响以及对工作人员的生命安全造成严重威胁,因此,矿山边坡中危岩体破坏机理的研究对于露天采矿工程具有重要意义。
地震是诱发危岩体失稳破坏的重要因素,岩质边坡的破坏形式主要受岩体结构控制[1],被垂直裂隙切割的岩体在受自身重力或外力作用下容易发生倾倒崩塌破坏[2],尤其在受到地震作用时,容易发生拉裂-倾倒破坏[3],已有学者对地震作用下危岩体的倾倒破坏进行了分析研究。薛新华等[4]利用UDEC 研究了地震作用下倾倒式危岩体的运动特征,并将落石的主要运动分为启动准备阶段,倾倒、翻滚阶段和减速滞留阶段。陈健云等[5]研究了水平地震作用下动水压力对倾倒式危岩体的稳定性影响。黄小福等[6]利用非连续变形分析法(DDA)研究了地震荷载对危岩体崩塌块体运动特性的影响。何思明等[7]基于岩石断裂力学研究了地震诱发岩体崩塌的力学机制,认为地震时崩塌本质上是地震波作用下危岩体裂缝扩展贯通的结果。唐红梅等[8]建立了考虑地震力作用方向下倾倒式危岩体最危险方向的物理力学模型,建立了倾倒式危岩体可靠度指标、失稳概率表达式及判断标准。
随着计算机技术的发展,数值模拟逐渐成为分析岩土工程、地质工程问题的重要手段,尤其是涉及到动力问题时,动力过程的复杂性使得物理试验较难进行和重复[9],然而采用数值模拟方法可以用较低的成本重复岩土体受动力作用下的破坏过程。当前确定性分析的数值模拟方法中包括连续介质分析和非连续介质分析两种,已有大量学者分别采用两种方法模拟边坡在动力作用下的响应特性和破坏过程,其中连续介质分析方法大多采用有限元法(FEM)[10]、有限差分法(FDM)[11],非连续介质分析方法大多采用块体离散元法[12-13]、颗粒离散元法[14]、非连续变形分析法(DDA)[15]等。单一的数值模拟方法往往会存在一定的缺陷,采用多种方法耦合的方式会达到扬长补短的效果。MA 等[16]采用颗粒离散元表示围岩,连续有限差分法区域表示隧道,利用FLAC3D-PFC3D耦合的方式从微观尺度上模拟了岩体的大变形破坏。TAN 等[17]采用刚性块体模拟石柱,摩尔-库伦连续体模拟周围土体,研究了软土中孤立石柱的破坏过程。BREUGNOT 等[18]利用FDM-DEM 耦合的方式研究了蜂窝防护结构受不同冲击作用下的响应。
基于前人研究,本文以新疆地区别斯库都克露天煤矿内某一危岩体为研究对象,采用FLAC-PFC 耦合的方式对强震作用下危岩体倾倒崩塌的启动机理、破坏过程进行了模拟分析。
1 连续-离散耦合方法
FLAC 采用有限差分方法将求解域划分为差分网格,利用有限个网格节点代替连续的求解域,经过多年的发展,FLAC 在计算效率、边界条件等方面都已经非常成熟。但是FLAC 在计算大变形问题时存在缺陷,由于其必须通过节点传递力和速度,因此所能模拟的变形量十分有限。颗粒流软件PFC 是一种离散元程序[19],与连续数值分析方法不同,离散元方法允许离散对象的有限位移和旋转,可以完全分离,对于大型滑坡等非连续问题的模拟具有一定的优势。PFC 基于力-位移定律和牛顿第二定律进行求解,力-位移定律是用于更新由每个接触点的相对运动造成的接触力,牛顿第二定律是用来确定每个粒子的运动力造成的接触和作用在粒子上的力。FLAC 和PFC 同是采用显式有限差分方法进行迭代求解,这为二者的耦合提供了可能。
FLAC-PFC 耦合采用wall-zone耦合方式,在连续网格与颗粒交接的地方生成与zone单元契合的wall单元,由FLAC 求解得到的速度通过耦合边界传递至PFC 模型部分,PFC 模型得到响应更新后,又通过耦合边界反作用于FLAC 模型,使FLAC 模型的力学响应得以更新(图1)。
早期研究中利用颗粒离散元方法分析动力问题时主要分为两种建模方法,其一是整体建模法,即完全利用颗粒建立边坡模型,而后在模型底部颗粒上施加速度来模拟地震波[20-21],但是这种方法生成的颗粒数量多,往往需要大量的计算时间,另外还需要利用Fish 语言在模型边界处编写动力波吸收功能,较为繁琐;其二是分开建模法,即利用wall单元建立模型的基岩部分,ball颗粒建立模型的危岩体部分,而后在wall单元上施加速度时程来模拟地震波[14,22],这种建模方法需要的颗粒少,也无需设置动力波吸收边界,但是却忽略了地震波在坡体内部的传递与反射。然而采用FLAC-PFC 耦合的数值模拟方法则可以解决上述问题,在进行动力作用数值模拟时,变形量较小的基岩部分利用FLAC 建立网格模型,将动力时程曲线输入到网格模型底部,既可以考虑动力波在模型中的传播特性,又可以利用FLAC 中自带的动力波吸收边界。变形量较大的危岩体部分采用PFC建立颗粒模型,可有效反映危岩体受动力作用时的大变形情况。
2 工程地质背景
别斯库都克露天煤矿位于新疆维吾尔自治区哈密市巴里坤哈萨克自治县,所在地区为典型的大陆性干旱和半干旱地区,其气候特征为干燥少雨,光照丰富,年温差、日温差大,降水发育不均;春季多风,冷暖多变,夏季酷热、蒸发强,秋季晴朗、降温迅速,冬季寒冷、低空气温稳定。该区域岩石颗粒间主要为泥质胶结、极少数为钙质胶结,在爆破、开采和降雨等影响下,岩石强度整体较低。区域内岩体层组可分为第四系松散岩组、风化软岩组、火烧岩破碎岩组和含煤岩组,其中第四系松散岩组覆盖最为广泛,呈散体结构,结构松散且孔隙度大。
黄润秋[2]将地震作用下边坡的破坏模式分为5大类,分别为溃滑型、溃崩型、抛射型、剥皮型和震裂型,其中溃崩型分为倾倒型、溃屈型、溃散型和溃喷型。倾倒型定义为近直立层状或似层状结构山体的浅表部,或近直立陡崖的强卸荷松弛带,强震作用下,陡立岩层顶部或中上部被折断、倾倒、摔出。残留岩层上常可见清晰张性折断面,表现为“断头”。图2 为岩体倾倒型破坏的典型示例图。通过对矿山危岩体潜在破坏类型排查,发现一危岩体与倾倒型崩塌的描述基本一致,如图3 所示,虚线框内为该直立危岩体所在位置,可以看到该危岩体为一直立结构岩体,节理裂隙发育,仅下部与周围基岩相连,在外力作用下容易沿底部发生整体倾倒破坏。
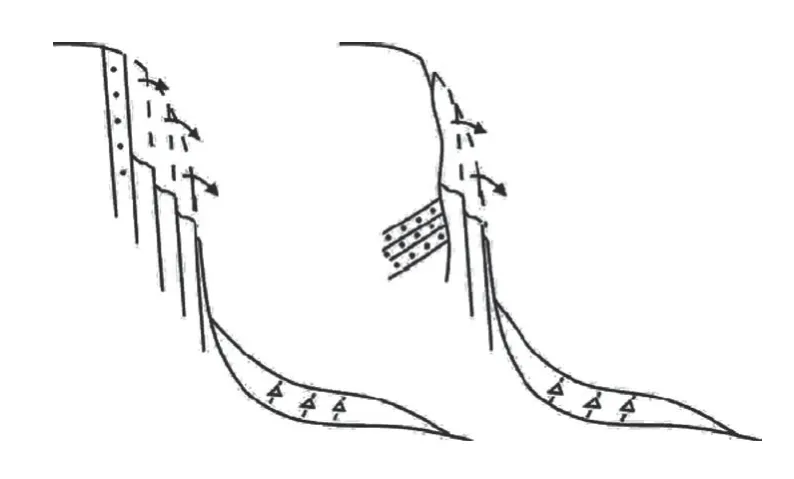
图2 倾倒型崩塌示意图Fig.2 Schematic diagram of toppling collapse
3 强震作用下危岩体倾倒崩塌破坏模拟
3.1 建立数值模型
为更好地理解该直立危岩体的破坏机理及过程,对该危岩体的倾倒崩塌破坏进行全过程模拟。为简化分析,视该直立危岩体为一整体岩块,并以此为基础建立如图4 所示的数值计算模型。数值计算模型的底部和左右两侧均采用连续区域建立,崩塌体采用离散颗粒建立,通过降低黏结强度的方法在离散颗粒中建立了一条裂隙。
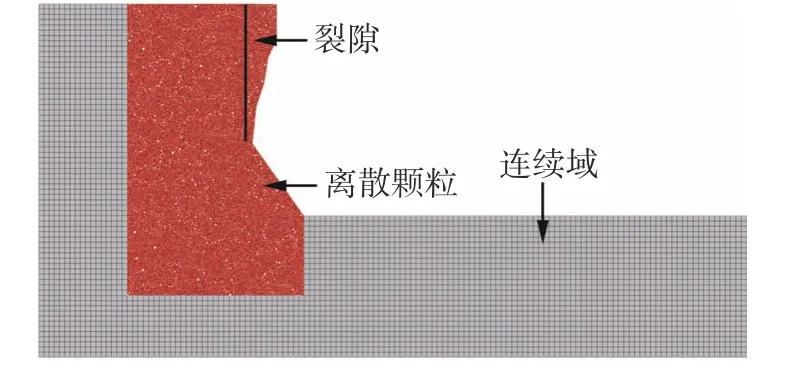
图4 数值模型Fig.4 Numerical model
3.2 微观参数标定
利用单轴压缩试验进行微观参数-宏观参数标定,宏观参数和微观参数见表1 和表2,已知试样弹性模量为20 GPa,泊松比为0.25,单轴抗压强度为12 MPa,通过试错法不断调整微观参数并进行压缩试验,得到PFC 试样弹性模量E为19.9 GPa,泊松比v为0.248,单轴抗压强度UCS为12.3 MPa(图5)。

表1 模型宏观参数表Table 1 Macroscopic mechanical parameters
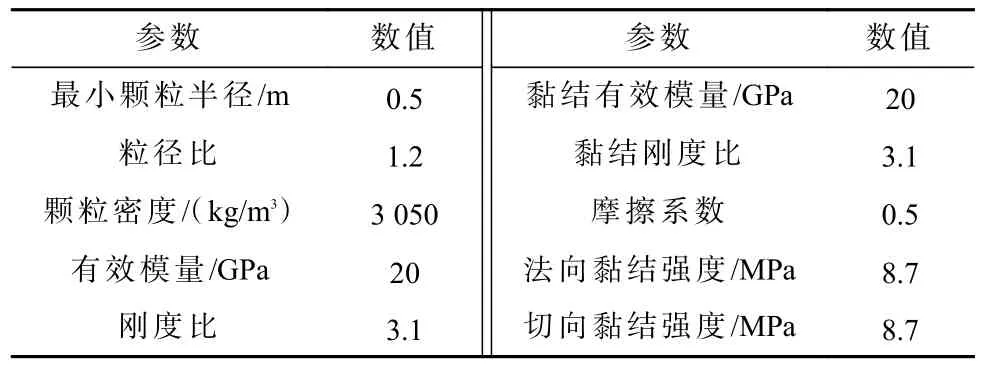
表2 模型微观参数表Table 2 Microscopic contact model parameters
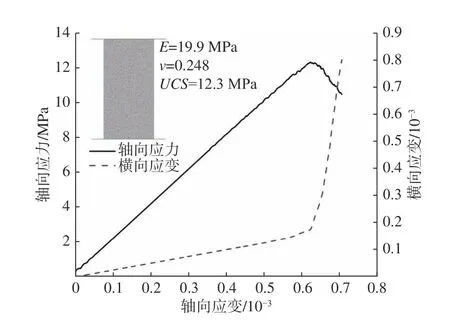
图5 单轴压缩试验Fig.5 Test of uniaxial compression
3.3 地震波的输入及验证
为保证地震波的准确输入以及模型边界对于地震波的有效吸收,模型两侧设置自由场边界,边界条件为底部全约束,两侧施加水平约束,地震波从模型底部输入,通过监测模型底部的速度时程曲线与输入速度时程曲线对比可证明地震波输入的正确性(图6)。通过在连续域与离散域耦合的交界处设置监测点以监测耦合效果,图7 为两个相近监测点的速度和位移曲线。由图7 可知,两点的速度曲线和位移曲线基本一致,因此可以证明耦合的有效性。
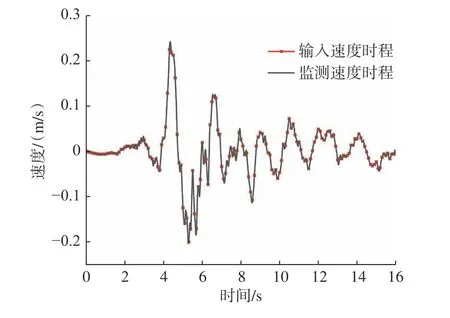
图6 地震波有效输入验证图Fig.6 Diagram of seismic wave valid input verification
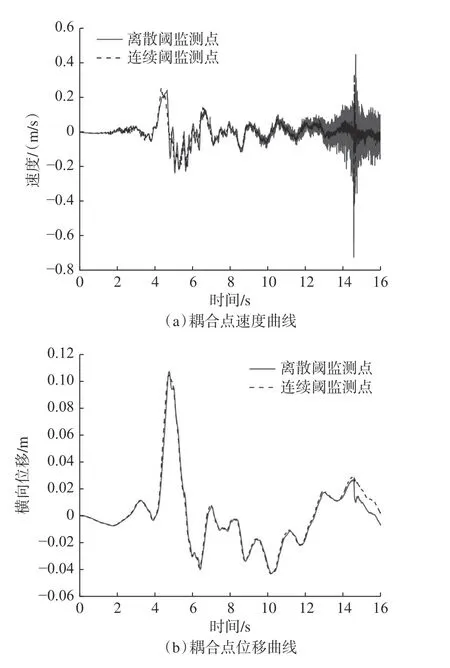
图7 耦合点监测曲线Fig.7 Monitoring curve of coupling point
3.4 数值模拟结果
图8 为崩塌破坏过程及颗粒速度图。从图8 中可以看到,在地震作用前4 s 时,崩塌体保持在相对稳定的状态,因为地震力作用在前4 s 的时候并不强烈,而当地震波作用到4 s 以后,在速度时程曲线上可以看到地震作用来到了第一个峰值点,此时在裂隙顶部产生了张拉破坏,随着地震作用的继续,破坏不断向下延伸直至产生自上而下的贯通裂隙,崩塌体开始出现倾倒破坏现象,整个倾倒破坏过程持续了10 s,崩塌体的上部速度明显大于下部速度。在第15 s 时,崩塌体撞击地面并破碎,崩塌体前缘被迅速向前抛出,平均速度达到了80~90 m/s,从颗粒轨迹跟踪图(图9)也可以看出,崩塌体上部在撞击破碎后被向前抛出。

图8 崩塌破坏过程及颗粒速度图Fig.8 Diagram of collapse process and particle velocity

图9 颗粒轨迹跟踪图Fig.9 Diagram of particle trajectory
从图10 中可以看出,崩塌体在地震作用第4.8 s开始出现破坏,张拉破裂迅速增加,崩塌体的平均速度和平均位移也开始慢慢增加,然后进入一个相对稳定的状态,平均速度和平均位移不断增大,在12 s时破坏崩塌体下部向下滑动,破坏继续增多直到14.8 s 崩塌体碰撞破碎,可以看到此时崩塌体的平均速度达到40 m/s,平均速度、平均位移和黏结破坏裂隙数量都有明显的突变。
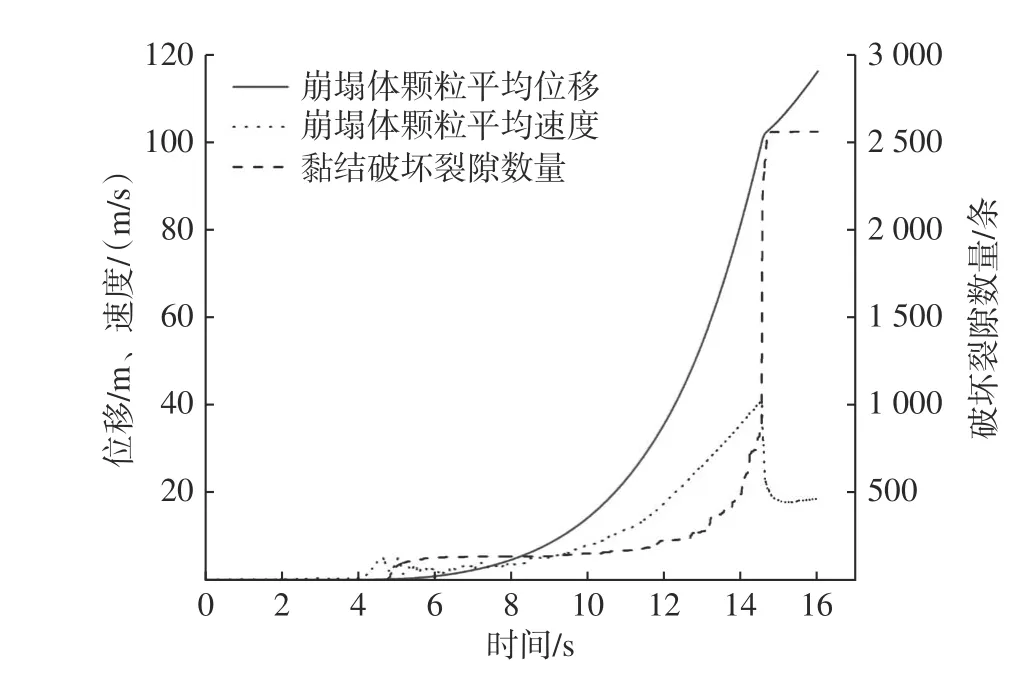
图10 崩塌体平均位移、平均速度及黏结破坏数量曲线Fig.10 Curve of average displacement,average velocity and quantity of bond failure of collapse body
根据崩塌破坏过程图以及监测曲线,将强震作用下倾倒型崩塌破坏分为以下四个阶段:相对稳定阶段,该阶段由于地震作用较弱,崩塌体整体处在一个比较稳定的状态;破裂贯通阶段,随着地震作用的加强,崩塌体进入一个拉裂破坏多发的阶段;倾倒滑动阶段,该阶段为裂隙完全破坏后,崩塌体整体向下倾倒;碰撞破碎阶段,崩塌体在倾倒碰撞地面后发生破碎。
4 讨论与结论
通过连续-离散耦合的方式模拟了动力作用下露天矿山中某一危岩体的倾倒崩塌破坏,分析了其破坏机理与破坏过程。连续-离散耦合的数值模拟方法适用于模拟地震作用下的边坡崩滑问题,一方面借助于FLAC 成熟的地震模拟方法和吸收边界条件,另一方面借助于PFC 从微观角度分析滑坡、崩塌的破坏机制及过程,研究成果可对露天矿山开采中危岩体防护提供借鉴。由于本文着重讨论连续-离散耦合方法下危岩体受地震作用的破坏机理和过程,并未对耦合模型的阻尼进行讨论,在利用耦合方法模拟地震问题时,如何合理设置阻尼条件需进一步研究,所得结论如下所述。
1)通过在连续域与离散域耦合的交界处设置监测点以监测耦合效果,可知两点的速度曲线和位移曲线基本一致,验证了FLAC-PFC 耦合方法模拟动力问题的有效性。
2)危岩体受地震作用后由上向下沿结构面产生裂隙,直到相对薄弱处,而后发生倾倒滑动破坏,崩塌体在撞击地面后发生破碎,前缘以巨大速度被向前抛出。
3)将强震作用下危岩体倾倒崩塌破坏分为四个阶段:相对稳定阶段、破裂贯通阶段、倾倒滑动阶段、碰撞破碎阶段。
