基于机器学习的电站耗水率计算及其对水位预测影响研究
2023-12-27王永强肖蕴珂
张 森,谢 帅,王永强,徐 杨,肖蕴珂
(1.长江科学院水资源综合利用研究所,湖北 武汉 430010;2.流域水资源与生态环境科学湖北省重点实验室,湖北 武汉 430010;3.三峡水利枢纽梯级调度通信中心,湖北 宜昌 443002)
0 引 言
耗水率指水电站总出力与发电流量的比值,是电站经济运行的重要参数。电站经济运行计算分为以水定电和以电定水,其运行精确程度与电站坝前水位与尾水位预测精度有重要联系。在水电站水位预测中,当前多使用耗水率经验曲线进行计算,其问题在于随着电站运行时间的延长,初期试验所测各变量以及变量间相关关系会发生较大变化,无法为水位预测等提供精确基础数据,难以匹配电网实时调控需求[1]。
近年来,机器学习与深度学习等人工智能算法在水电站应用成为热点[2],机器学习方法凭借其强大的变量拟合能力,提供了新思路来克服传统水位预测框架无法精确描述变量函数关系的缺点[3]。刘涛等[4]学者使用LassoLarsCV模型对长寿站的坝前水位做出了回归计算,将预测误差控制在1.2 m以内;徐杨等[5]学者采用BP神经网络模型构建了非弃水期的下游水位预测方法,应用于葛洲坝水位预测中,取得了高精度的预测效果;纪国良等[6]学者采用循环神经网络系统,学习入库流量和坝前水位到目标站点水位的映射关系,取得了优于水力学模型的站点水位预测结果;贾本军等[7]借助SVR算法探究了电站尾水位的关键影响变量以及计算特性。
综上所述,诸多学者的研究侧重于在研究变量响应关系的基础上,算法在预测问题中的直接应用。而使用算法进一步探究水位预测中关键变量的影响因素与拟合方法,并探究其对水位预测影响的研究却较少,且对水电站精细化运行有着重要意义。因此本文基于传统水量平衡方法的水位预测框架,构建出2 h时段三峡水位预测模型,在此基础上使用机器学习的不同算法提高耗水率,尾水位的计算精度,进而提高水位预测精度,得出该改进对上下游水位预测带来的影响。
1 基于水量平衡的三峡水库水位预测模型
1.1 水位计算模型框架分析
图1为三峡水位计算要素图与计算流程,可将其划分为上游部分、水坝部分、下游部分3个环节。上游计算环节是水位-库容的转换计算,库容的计算即水量平衡方程为
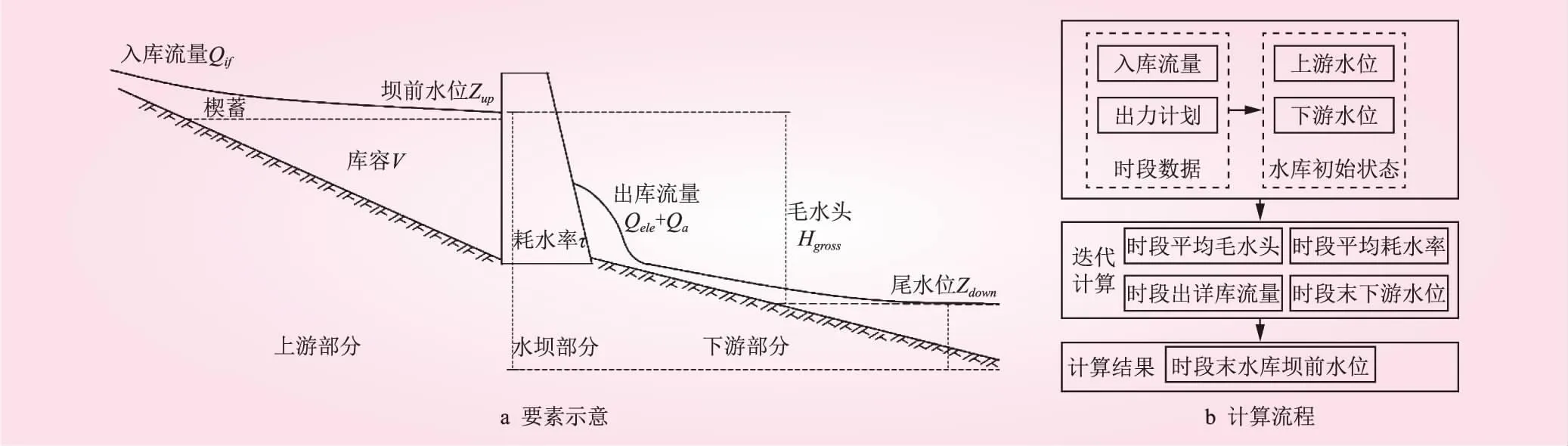
图1 三峡水位计算示意
(1)
Vt-1+(Qif-Qele-Qa)Δt=Vt
(2)
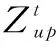
第2环节依据毛水头计算耗水率,耗水率与水电站规划出力乘积即为出库流量,反馈至第一部分水量平衡方程计算时段末库容和时段末坝前水位。第3环节下游计算通过出库流量计算尾水位。耗水率的计算精度与时段平均出库流量精度直接关联,参与到水量平衡计算之中,进而影响到时段末预测水位的精度。计算公式为
(3)
Qele=τNt
(4)
(5)
1.2 使用机器学习的模型改进思路
基于上述的计算思路和公式,可以构建出基于水量平衡的时段迭代水位计算模型,目前电站对模型中式(3)与式(5)的计算依赖于经验曲线,计算耗水率使用毛水头-耗水率经验曲线,计算下游水位使用出库流量-尾水位经验曲线,而耗水率的计算精度决定出库流量的计算精度,因此耗水率高精度计算是提高水位预测精度的基础;提高尾水位计算精度不仅是提高耗水率拟合精度的支撑,也是水位预测问题的目标之一。针对两经验曲线计算误差大的问题,本文提出,在水量平衡法模型的基础上使用机器学习算法,替换耗水率、尾水位计算使用的经验曲线法,以提高三峡水位预测的精度。
2 基于机器学习的电站耗水率和尾水位计算模型
2.1 机器学习方法的应用思路
机器学习是一种新的编程范式,根据大量特征变量与对应目标值,模型将按照自身规则框架进行学习训练,得到变量相关关系与权重参数。不同机器学习算法有着不同规则框架,需根据计算情景做出选择[8]。
电站出库流量是影响电站尾水位的关键因素。下游水库的水位和区间来水会对本水库的尾水位有顶托作用,因此需将三峡下游的葛洲坝电站上游水位也作为变量考虑在内,三者的关系可以表示为
(6)
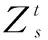
模型中耗水率拟合方法是毛水头-耗水率曲线插值。这一曲线的原理是水电站出力计算的NHQ公式,表示为
N=KQH
(7)
(8)
式中,N为时段平均出力;Q为发电流量;H是时段平均毛水头;K为系数,与机组效率有关。经验曲线认为τ与H相关关系显著,因此使用毛水头作为耗水率的查值判断条件。实际上耗水率的拟合需考虑不同工况导致K值的变化,对此类影响因素多且复杂的拟合关系,可采用SVR(支持向量回归)或KNN(K近邻分类)算法进行拟合,考虑的变量有时段调峰、时段出力、毛水头、三峡上下游时段平均水位。
2.2 构建耗水率机器学习计算模型
耗水率的拟合比较了SVR和KNN两种算法。支持向量回归(SVR)是支持向量机(SVM)的延申[9],SVM是一种二分类算法,即在高维空间的样本点集中获取一个超平面,使不同类别的样本点距离该超平面最远,目标函数为
(9)
支持向量回归正相反,其目标超平面要使得各个点距离其最近,以此认为该超平面能够描述点集分布特征规律。K近邻回归(KNN)本质则是一种多项分类[10],原理为根据给定的多个类,及其对应特征值,构建高纬数据点集,当输入某个未知类的特征值时,计算距离其欧氏距离最近k个数据点,以k个数据点中最多的类别作为未知类的类别[11]。当模型以耗水率所对应的特征变量为类的特征值,耗水率值为类本身构建高维数据点集,就可以从广泛的样本中寻找到最符合当前机组工况的耗水率值,其训练速度快,计算方便,对样本充足,变化范围小的计算目标变量有着很高的计算精确度。2种模型构建时使用相同的数据集,目标变量为耗水率,特征变量采用时段调峰、时段出力、毛水头、三峡上下游时段平均水位。
SVR模型构建主要考虑核函数、gamma参数与正则化系数[12],可在构建模型后,从数据集中随机取数,采用不同参数做交叉检验,使用最好拟合效果的参数进行建模,最终确定SVR模型核函数选为rbf,gamma参数选为scale,正则化系数为0。KNN算法训练速度快且参数简单,可以直接使用整体数据集来训练寻优,得出结论模型的K值选为3,算法选择kd_tree时具有最好效果。预测效果采用平均误差MAE与最大误差MAXE来评判,如表1所示。

表1 KNN方法、SVR方法、曲线插值法计算耗水率平均误差与最大误差
三峡的耗水率平均值为11.7,使用插值方法平均误差为1.59,KNN方法平均误差为0.063,SVR方法平均误差为0.242。本实验验证集使用了2 100组数据,训练集使用了18 900组数据,大量训练集数据保证了KNN算法的整体准确率,相对于SVR方法和曲线插值法在整体上有着很优秀的预测成果。3种方法进行整体对比后本文选取KNN算法作为耗水率的率定方法。
2.3 构建尾水位机器学习计算模型
尾水位的计算采用的是机器学习中的多元线性回归(Linear Regression)[13],这是一种较为简单的回归模型,认为所输入的特征变量关系为加权平均,数据清洗校正,去除异常值后,将训练计算经过特征化后的变量的权重以完成拟合。本次回归计算的特征变量有三峡电站出力、三峡电站出库流量,以及下游的葛洲坝水电站的上游水位,以减小因为下游顶托所带来的计算误差。考虑到3者的可能存在的相关关系可能较为复杂,在使用Polynomial Features函数对训练数据做特征转化时,分别对特征值多项式次数(degree)为1~5时做了测试,得到结果见表2。
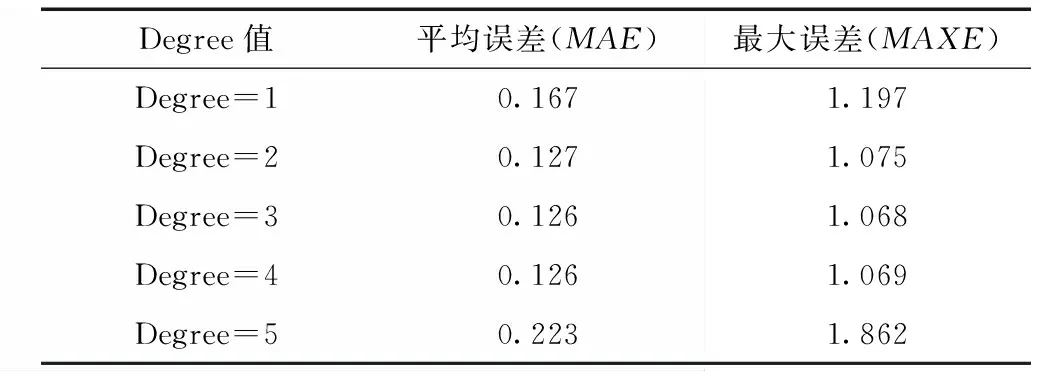
表2 机器学习多项式回归不同degree值计算尾水位平均误差与最大误差 m
当次数在2、3、4时计算精度大致相同,而次数增加到5则由于特征数由34变为35增幅过大,影响回归判断,导致误差突增。最终选取degree为3时的训练成果与预测效果来和曲线查值法的预测效果进行比较,观察其改进程度,结果如表3所示。

表3 水位平均误差与最大误差 m
相比于此前物理模型中采用的曲线插值,机器学习的计算下游水位的整体误差由0.269 m缩小到0.126 m,最大误差由1.261 m缩小到1.068 m。整体计算精度有较大提升,最大误差有一定缩减,能够为提高三峡坝前水位预测提供一定支持。
3 模型计算结果
在使用机器学习方法分别构建了耗水率和尾水位计算模型后,将二者应用于前文所述的水量平衡方法的水位预测模型中,以替换经验曲线查值方法,并对替换前后模型的计算结果进行分析。
3.1 替换前水位预测模型计算结果分析
使用基于水量平衡计算框架构建的水位计算模型,不替换耗水率和尾水位的计算方法,选取2020年~2022年这3年对三峡坝前水位进行2 h时段预测。计算所使用的数据包括三峡上下游代表站整点水位数据、时段平均出力与流量数据,以及特征曲线。特征曲线包括水库库容-坝前水位曲线、毛水头-耗水率曲线、出库流量-尾水位曲线,所有数据均取自于三峡电站历史运行数据记录。误差的评价指标采用平均绝对误差(MAE)与最大绝对误差(MAXE),公式为
(10)
MAXE=max(|ymeasure(i)-yestimate(i)|)
(11)
式中,ymeasure为测量得到的实际值;yestimate为计算值。
三峡电站汛期为6月~9月,结果显示,大幅度误差集中在这一时段。水库的入库流量较大,受调峰影响,导致耗水率、发电流量预测误差偏大,引起水位预测不准确。选取2022年误差分布图,按汛期和非汛期进行展示如图2所示。表4为坝前水位和尾水位计算的平均绝对误差(MAE)与最大绝对误差(MAXE)。图3为不同区间的误差占比分布。

表4 传统模型水位预测误差统计值 cm
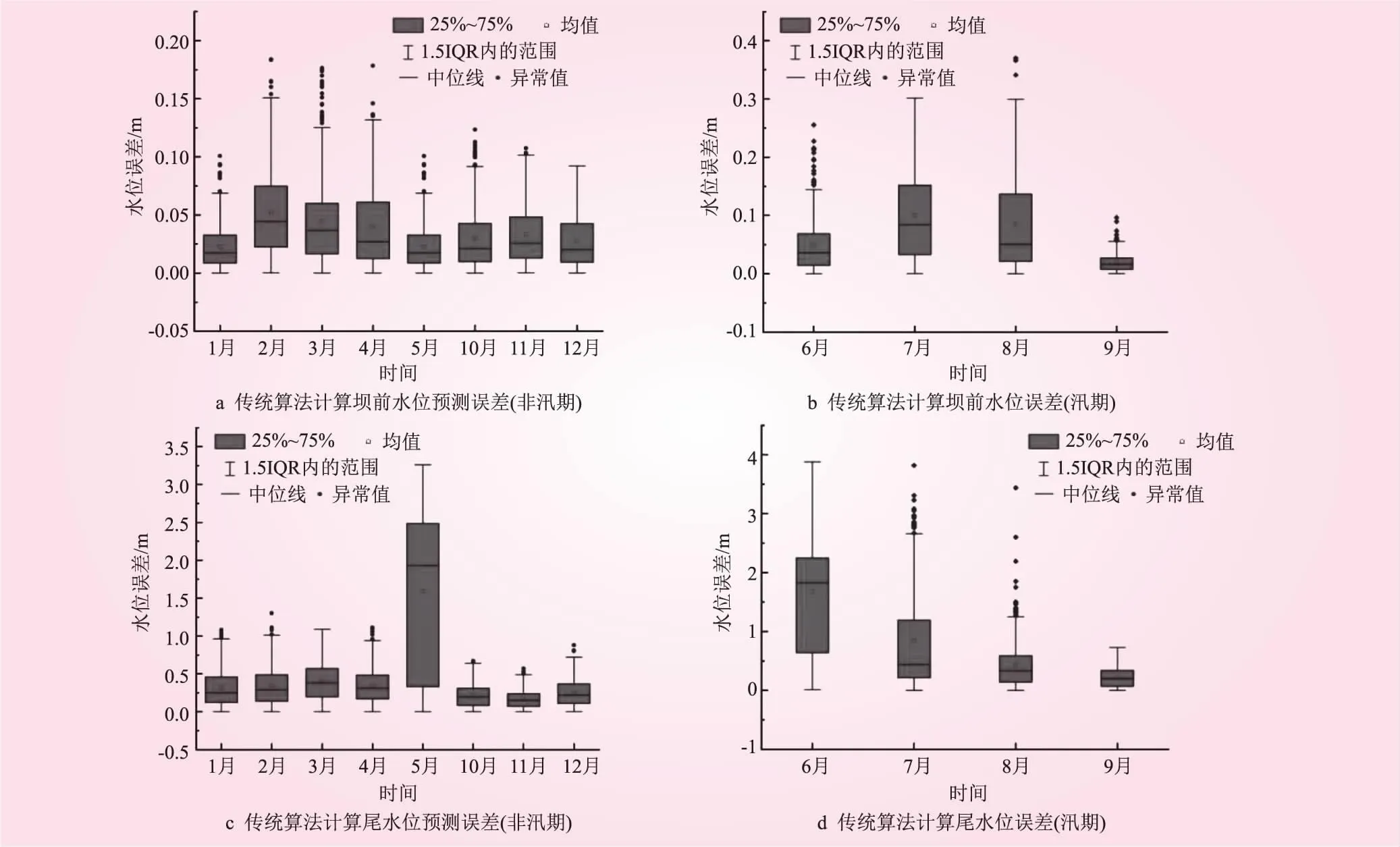
图2 传统模型预测坝前水位与尾水位误差分布
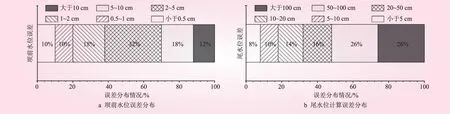
图3 2022年传统模型预测三峡水位误差分布
与真实值相比,2020年~2022年水量平衡模型耗水率平均绝对误差(MAE)为0.137,最大绝对误差(MAXE)为1.371。误差分布如图4所示。
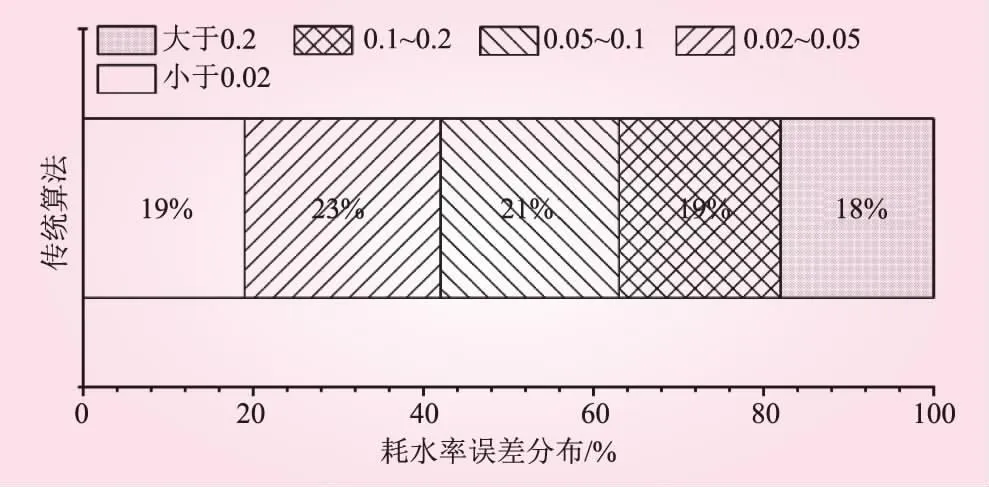
图4 传统模型拟合耗水率误差分布
三峡电站耗水率分布为10到15,计算结果表明,耗水率最大绝对误差为1.37,所对应耗水率值为13.8,误差幅度约10%,耗水率平均值为13.2,平均绝对误差幅度为平均耗水率的1%。
3.2 替换后水位预测模型计算结果分析
使用上述机器学习方法代替了模型中的经验曲线后,同样将模型应用于三峡水电站的2 h时段水位预测中,计算2020年~2022年这3个年份的数据,以2022年为代表,划分汛期与非汛期展示如图5。
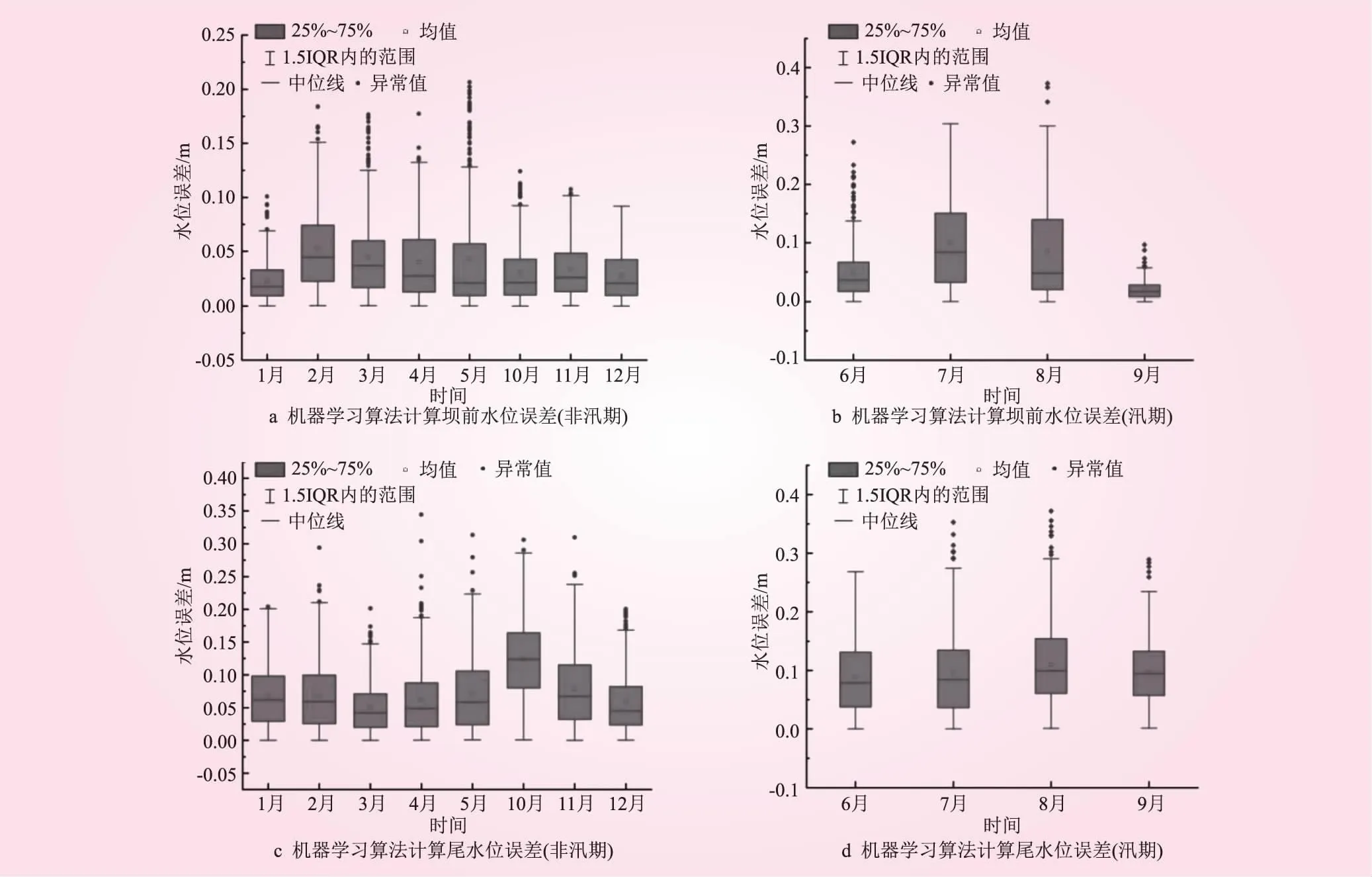
图5 机器学习改进模型计算三峡坝前水位与尾水位误差
表5为改进后模型计算三峡水位误差值统计,表6、7为三峡大坝前、尾水位改进前后年均误差对比。从表中可知,三峡坝前水位预测精度的提升较小,MAE降低幅度约为10%。尾水位的计算精度提高明显,MAE由102 cm降低至11.37 cm,MAXE由521 cm降低至101 cm,误差降低幅度约88%。
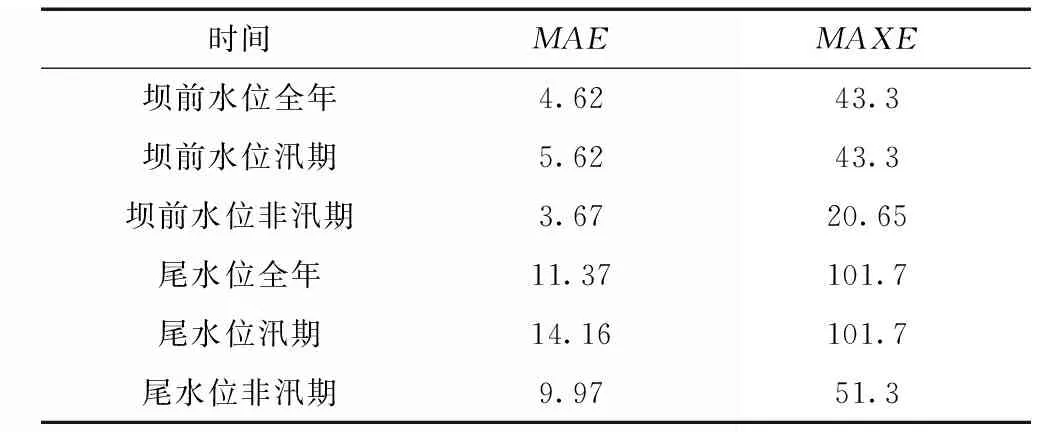
表5 机器学习改进模型预测三峡水位误差 cm

表6 模型改进前后三峡坝前水位预测误差对比 cm

表7 模型改进前后三峡尾水位预测误差对比 cm
4 误差讨论分析
计算结果表明,借助机器学习改进模型后对坝前水位和尾水位有不同幅度的提升。为了探究耗水率计算方法改进对水位预测计算带来的具体影响,以及计算误差来源,对改进前后的耗水率、出库流量这两个重要变量进行输出分析。
4.1 耗水率计算分析
对计算过程中耗水率的计算进行输出,误差分布对比如图6,误差统计如表8所示。

表8 机器学习改进前后耗水率计算误差分布对比
从表6~8、图6可知,改进后模型计算耗水率MAE降低约64%,计算年份内三峡电站平均耗水率为11.17,改进前MAE为其1.2%,改进后MAE为0.43%。出库流量误差统计分布表如表9所示。弃水为0的情况下,耗水率与出库流量为正比,出库流量的平均绝对误差也将会降低与耗水率相应的幅度。

表9 机器学习改进前后出库流量计算误差对比 m3/s
4.2 出库流量分析
输出三峡坝前水位计算过程中,三峡出库流量误差分布情况如图7所示,误差分布统计值如表9。
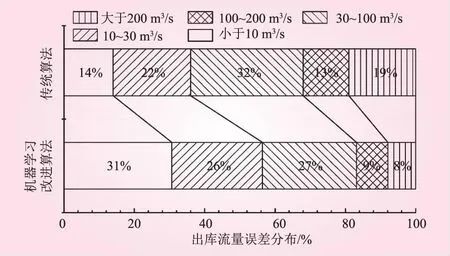
图7 传统模型与机器学习改进模型计算出库流量误差分布
改进前后的模型计算出库流量的MAE分别为205.62 m3/s与61 m3/s,最大误差分别为2 211 m3/s和1 313 m3/s。二者降低幅度都较为显著,与耗水率误差的降低幅度契合。表10反映了模型计算得到的年均出库流量与真实值的差距,改进后的模型年均出库流量计算值与平均值最大不超过4 m3/s。
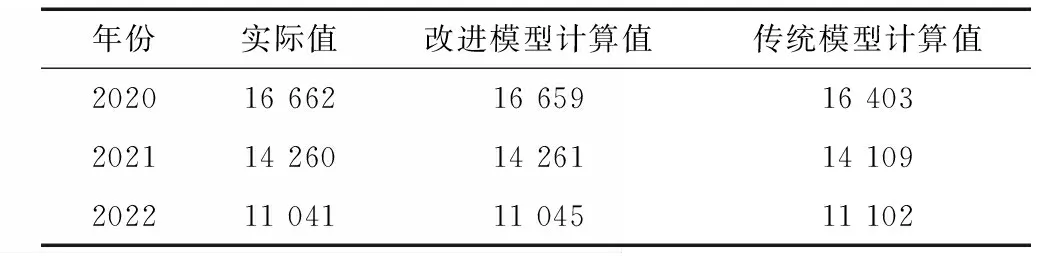
表10 年均出库流量真实值与模型改进前后计算值对照 m3/s
模型计算得到的上游水位平均值与真实上游水位平均值对比如表11所示。
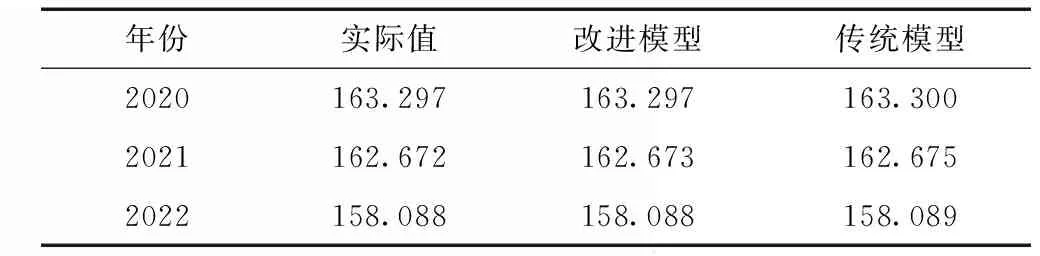
表11 年均上游水位真实与模型改进前后计算值对照 m
从表11可知,年内平均上游水位误差由2 cm左右降低到了不超过4 mm。
本文的预测时段为2 h,出库流量的平均绝对误差降低了144 m3/s,这一值在2 h时段上引发的水量误差约为103.7万m3。根据三峡的水位库容曲线,坝前水位在161 m时,提高10 cm水位库容约增大5 000万m3,103万m3的水量对水位约造成2~3 mm的影响。与上文得到的平均水位绝对误差降低幅度相符合。
4.3 分析总结
改进后模型将计算过程中的耗水率、出库流量计算误差降低60%以上,出库流量的计算精度提高以及尾水位计算方法的改进,使三峡尾水位计算绝对平均误差降低约88%。同时,以年尺度来看,计算平均水位与真实平均水位仅有最多0.4 cm误差。这表明改进模型在计算方法改进层面取得了较好的效果。坝前水位计算平均绝对误差降低10%,在耗水率、出库流量计算精确度显著提高的情况下,应进一步考虑由于动库容导致的库容-坝前水位经验曲线不准确问题所引起的误差。
5 结 论
本文以三峡电站为对象提出了基于机器学习的精细化计算方法,通过模拟对比分析,所提出的方法对二者的拟合精度有显著提升效果。在三峡2 h时段水位预测中,降低耗水率预测误差60%以上;坝前水位的误差控制在44 cm以内,平均绝对误差降低约12%;尾水位误差控制在1 m以内,平均绝对误差降低约88%以上。可为三峡电站发电计划编制和厂内经济运行提供较好的支撑。
