渠道预制块自动化铺装机械检测定位技术研究
2023-12-27吴立韬田正宏
吴立韬,孙 啸,田正宏
(河海大学水利水电学院,江苏 南京 210024)
0 引 言
渠道护坡常常采用预制块进行铺装保护。预制块主要由混凝土制成,其独特的连锁式设计[1]对于防止水浪冲刷具有良好的整体稳定性。预制块外形不规整、质量大、铺装精度要求高、间隙咬合紧密的特点导致预制块铺装施工困难。目前预制块的铺设主要由人工来完成,存在工作强度大、效率低、安全性低的问题。如何根据现场情况设计实时调整铺装动作的自动化铺装机械,是解决人工铺装弊端的有效方式。
自动化铺装机械的设计模式多样,设计限制由所处的环境决定。对于室内铺装,环境变化较小,对铺装机械的体形限制较大;对于室外铺装,环境变化大,对铺装机械的环境适应性限制就高。近年来,在自动化铺装机械领域已有学者进行相关的研究。2010年,tinger-stone自动铺路机在荷兰问世,利用砖块自身重力码放,需要工作人员协助装料。2013年程明等[2]提出一种集运砖、刷浆、铺砖、压砖等多道工序于一体的自动化铺砖解决方案。Usmanov等[3]提出了一个通用的方法来创建一个砖砌墙建筑系统,该系统提出了机器人系统在施工物体内部的最佳位置,即,使机器人的运动距离最小化,从而减少施工过程的电力消耗。Wu等[4]以实际砌砖工程为例,利用概率路径方法对六轴机器人进行运动规划。Yu等[5]对基于最优布局方式和轨迹算法的机械手集成移动系统进行研究,采用“快速算法”设计了模式生成器,并采用“重叠法”开发了机器人轨迹生成算法。但是现有的智能化铺砖机械适用于平整且相对结实的地面路基,铺装的对象以方砖为主,砖块之间卡接顺畅,基底平整无变形无坡脚。采用这类机械式自动化铺砖方法与机械,无法有效解决斜坡面松软垫层面、重型大尺寸、互相咬合砌块的精准对位和高效铺装问题。
对于砖块检测识别,Chattopadhyay等[6]设计一种基于动态视频流的实时图像分割方案,用于移动机器人中的目标定位,算法具有很高的时间效率,适用于两个移动机器人实现多智能体交互协调,如比赛、目标跟踪和砌砖等。Zandavali等[7]提出了一种基于图像到图像翻译的机器学习自动砖瓦加工框架。该框架包括创建数据集、为每个纽带训练模型以及将输出图像转换为机器人装配的矢量数据。Malakhov等人[8]提出采用数字驱动以及优化设计和算法解决方案被认为是提高移动砌砖机器人能源效率的手段。然而,在渠道预制块铺装机械领域,图像处理和定位技术尚未得到成熟的运用,针对现有对渠道预制块铺装研究的不足,本文设计渠道预制块铺装机械所需的检测定位技术,将图像处理系统、定位计算系统与机械系统相结合,实现对预制块铺装点的精准预测与顺利铺装。
本文研究内容:①使用图像预处理后的目标检测算法,结合点云计算实现对预制块检测和定位。②根据预制块模型建立数据集,实现对预制块铺装点的预测。④设计预制块铺装机械的机械系统,并进行铺装试验。
1 渠道预制块铺装机械
渠道预制块铺装机械包含图像处理系统、定位计算系统、机械系统。图像处理系统获取预制块图像,对限制待铺装位预制块的相邻预制块坐标进行计算,并将数据传输给定位计算系统。定位计算系统根据输入数据,对待铺装位置计算,再将待铺装预制块的坐标传输给机械控制系统,机械控制系统根据坐标,将预制块放置于预定位置。
1.1 图像处理系统
图像处理系统通过结构光相机采集彩色图和点云图,图像处理系统采用PDN700结构光相机,采用850 mm的光源,工作距离为300~700 mm,近端视场为265 mm×235 mm,Z轴精度在0.1 mm,对深度图的分辨率在1 280×1 024,对彩色图的分辨率在1 280×1 024,采集时间在1 s左右。
图像处理系统的总体流程如图1所示:①结构光相机采集彩色图和点云图。②目标检测算法对彩色图进行目标检测。③计算彩色图中目标区域的范围。④根据彩色图中目标区域的范围提取点云中的目标区域。⑤计算预制块的中心坐标点。
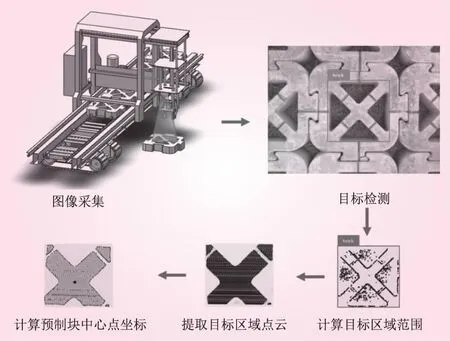
图1 图像处理系统总体流程
1.1.1 目标检测算法
(1)图像预处理。图像预处理可有效改善原始图像质量,突出检测目标。目前常用的图像预处理手段有灰度变换、滤波去噪、图像锐化等。渠道预制块铺装机械处于室外开放环境中,存在太阳直射、目标物不清晰、目标物背景复杂等问题。因此采用多种图像预处理方式,减小背景物的干扰,强化目标物体的轮廓,目标检测算法的训练精度和速度。图像预处理步骤效果如图2所示,具体流程为:①使用Canny[9]对原始图像2a处理,通过高斯滤波、非极大值像素梯度抑制等算法检测图像边缘、将非图像边缘抑制,处理效果如图2b所示。②预制块的材质、灰尘、污渍使得Canny算法对图像的处理效果未达到预期,使用Dilated[10]继续处理。通过10×10的内核对图像处理,取核中像素值的最大值代替锚点位置的像素值,将图像中的高亮区域膨胀,使得预制块边缘部分更加明显,处理效果如图2c所示。③经过Dilated处理后的图像,仍不能将目标物和背景较为清晰地区别开来,使用Thresholding[11]继续处理,设置阈值将图像分成二值图像,处理效果如图2d所示。④处理后的图像除了预制块的轮廓外,还存在较多干扰点,使用Eroded[12]继续处理。通过5×5的内核对图像处理,取核中像素值的最小值代替锚点位置的像素值,将图像中的白色部分缩减细化,得到目标物更加凸显的图像,处理效果如图2e所示。
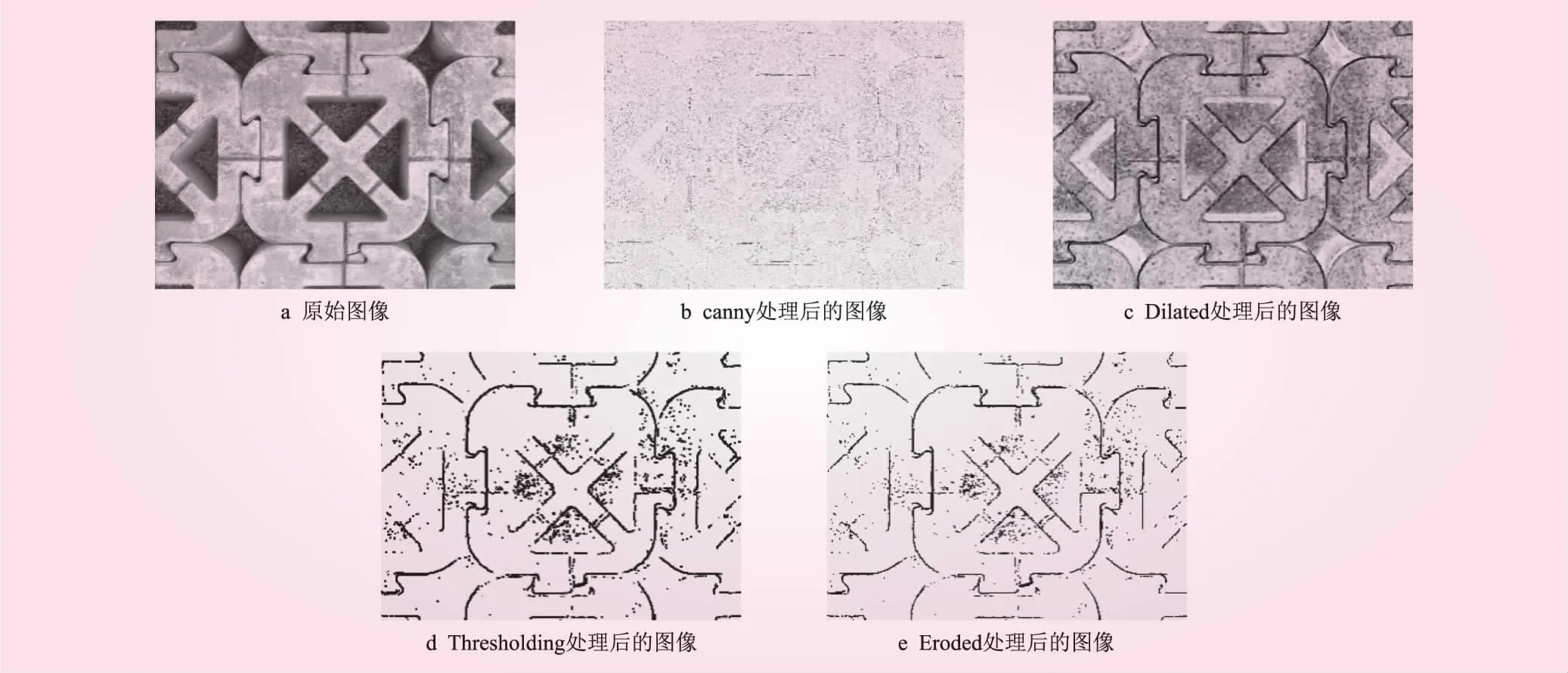
图2 图像预处理各步骤效果
(2)YOLOv5s结构。YOLOv5s[13]算法主要结构分为主干特征提取网络、加强特征提取网络、目标检测分类器。主干网络主要由Conv、C3、SPPF3个模块组成,将输入图片转为特征集合。输入图像数据大小为640×640×3,使用图像预处理后,图像通道数降低,图像大小为640×640×1,可以提高模型的运行速度。加强特征提取网络采用FPN+PAN[14]结构,通过80×80、40×40、20×20等3个尺度对目标进行检测,经过NMS(非极大值抑制)按照概率值筛选剔除冗余的预测框,最终输出置信度最高的预测类别和边界框的位置坐标。
1.1.2 目标定位算法
根据彩色图的目标区域对深度图目标区域划分后,计算预制块的中心坐标和旋转角度。目标定位算法如图3所示。目标定位算法的流程为:

图3 目标定位算法各步骤示意
(1)使用Pass Through算法[15]与Ransac算法[16],将原始点云图像的z方向设定数值段以外的点全部去除。在图像采集时,预制块与深度相机的距离固定,因此,只需保留固定距离的点云,去除噪声,提升速度和精度。再对滤波后的深度图提取平面,在深度图中随机选取3个点,计算其他点到该平面的距离,若小于设定的阈值则认为属于同一个平面。如此往复迭代直到所有点满足,处理效果见图3b。
(2)使用Boundary Estimation算法[17],对平面提取后的深度图进行边界提取,先进行局部采样获取局部平面,以最小二乘法拟合该局部平面,并将其向微切平面投影,根据采样点与其近邻所对应投影点连线的最大夹角识别散乱点云边界特征,处理效果如图3c所示。
(3)预制块的深度图像中,有4条直线靠近图像中心,两两相交。提取出4条直线,并计算出4条直线的表达式。根据4条直线的表达式,计算出直线的交点,取交点横纵坐标的平均值为预制块的中心点。根据直线的斜率,计算直线的倾角与45°、135°的差值,从而计算预制块的旋转角度,处理效果如图3d所示。
1.2 定位计算系统
定位计算系统通过建立预制块的模型,并通过调整预制块间距和旋转角度模拟铺装来获取试验数据。根据不同的工况采用其对应的算法,输出待铺预制块的铺装坐标信息。
1.2.1 模型参数
根据现场测绘建立预制块模型,如图4a所示,预制块有两个凸块部分和两个凹槽部分,形状与大小完全一致。预制块的铺装要求铺装的预制块的凸块与相邻预制块的凹槽相契合。为了保证铺装时预制块间不会相互碰撞摩擦,以预制块凸块在相邻预制块的凹槽中,且凸块与凹槽的间距最大为佳,可将模型简化为预制块间凸块和凹槽的位置关系,如图4b所示。为了限制住凸块处于凹槽的包围中,根据预制块模型建立凸块点模型和凹槽线模型,计算出凹槽包围的范围内点的取值范围,以限制凸块的位置。若凸块点模型超出取值范围,将舍去该数据。

图4 预制块铺装示意
预制块间凸块与凹槽的间距受预制块间的相对位移和相对角度共同影响,如图4c所示,对于①②两块预制块,在相对旋转角度为α的情况下,②号预制块沿x方向的位移dx和沿y方向的位移dy与②③两块预制块,在相对角度为α,③号预制块沿x方向的位移-dy,沿y方向位移预制块间距一致。因此,只需对①②两块预制块的不同相对位置和旋转角度下的工况模拟即可推出①②③3块预制块间不同相对角度和位移下的间距。
对凸块点模型沿x方向位移dx,沿y方向位移dy和旋转α角度操作,若初始点坐标为(x,y),经过位移、旋转后的点坐标(rmx,rmy)为
(1)
(2)
对于点总数为n的凸块点模型,凸块上第i个点pi到凹槽线模型最小间距为
dpi=min(dl,dc),(1≤i≤n)
(3)
计算所有点到凹槽线模型的最小间距,其最小值即为凸块至凹槽的最小间距为
d=min(dp1,dp2,…dpi…,dpn),(1≤i≤n)
(4)
1.2.2 工况模拟
预制块铺装过程分为单边限制和双边限制2种工况。当渠道预制块铺装机械进行每一列(第一列除外)预制块中第一块预制块的铺装时,待铺预制块只受到单边限制。当铺装机械在完成每一列第一块预制块的铺装后,继续往下铺装时,待铺预制块受到双边限制。
(1)单边限制。待铺装预制块为②预制块,对其单边限制的预制块为①预制块。当预制块间的夹角为0°,预制块间间距为l时,①预制块与②预制块的间距最大,此坐标点作为②预制块的铺装坐标。根据①预制块相对铺装机械的坐标x1、y1、α1,计算出②预制块的中心坐标为(x1-lcosα,y1-lsinα)。
(2)双边限制。待铺装预制块为②预制块,对其双边限制的预制块为①③预制块。设置②和③预制块相对①预制块的位移量和旋转角度分别为x2、y2、α2和x3、y3、α3。③预制块相对于②预制块的旋转角度为(α3-α2),x方向位移为(x3-x2),y方向位移为(y3-y2)。将②预制块x方向位移m1次,y方向位移m2次,计算每次位移时,其与相邻预制块①和③预制块的间距d1和d3。再计算②预制块与相邻预制块最小间距
dk=min(d1,d3)
(5)
以①和③预制块的相对旋转角度和相对位移为前提,计算②预制块相对①预制块不同旋转角度和相对位移下,①②③预制块的间距,取其间距最大情况下的旋转角度和位移点,视为最佳旋转角度和位移点,即
dkbest=max(dk1,dk2,…,dki,…,dkn)
(6)
1.2.3 蜣螂算法优化的BP神经网络
基于蜣螂算法优化的BP神经网络(DBO-BP)用于对双边限制条件下的预制块铺装位置的预测,是将蜣螂算法[18]和BP神经网络[19]相结合的算法。BP神经网络是以梯度下降的方法获取最终解,但是梯度下降的方法与梯度下降的初始值有较大关系,而导致最终解为局部最优的情况。蜣螂算法模拟蜣螂动作,将最优解通过迭代的方式留下。为此,将蜣螂算法和BP神经网络相结合,可以弥补BP神经网络的不足,如图5所示。该算法具体步骤如下:
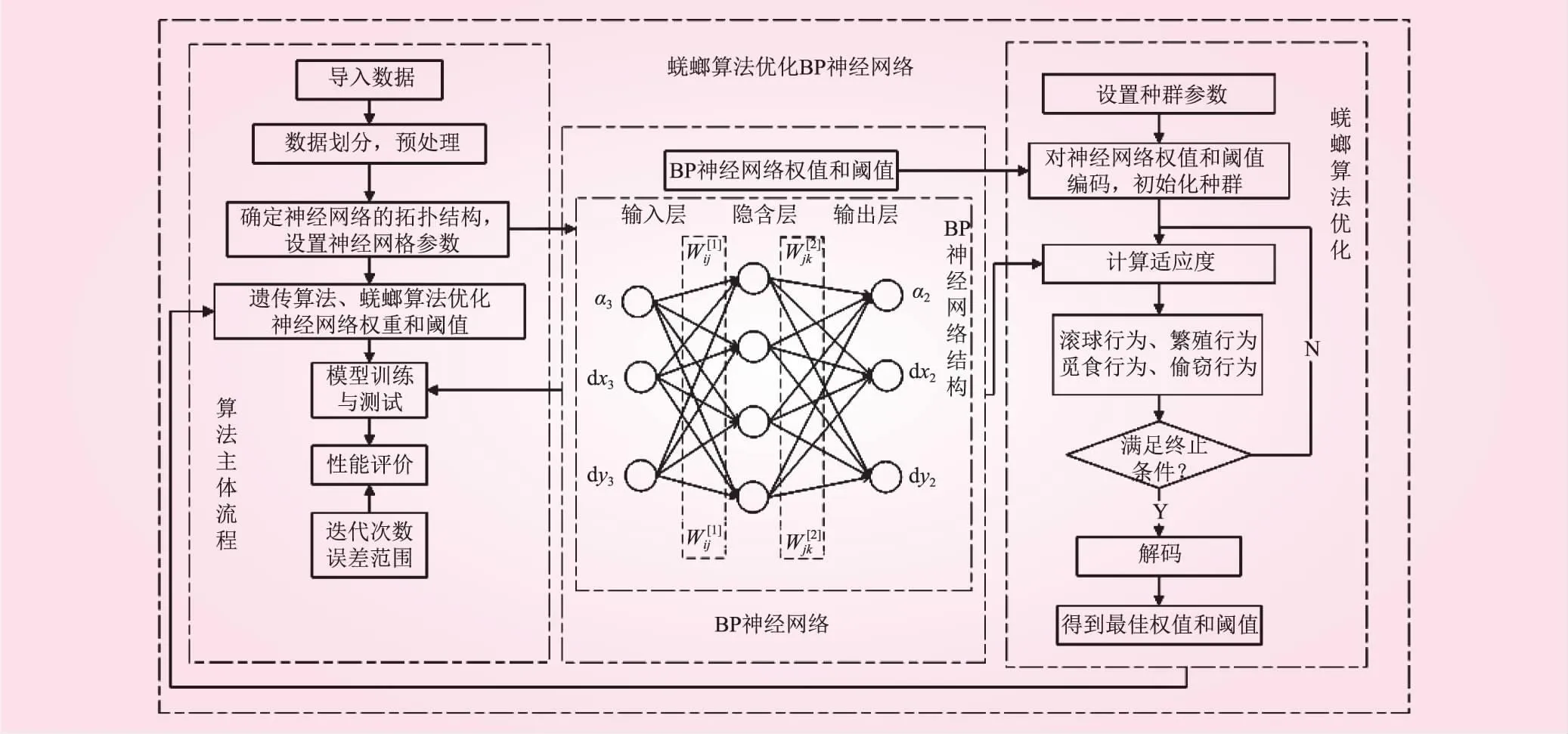
图5 蜣螂算法优化的BP神经网络示意
(1)将护坡上③预制块与①预制块间的相对角度α3和相对位移x3、y3作为输入层神经元参数,将待铺装的②预制块的与①预制块间的相对角度α2和相对位移x2、y2为输出层神经元参数,划分完数据集后对数据进行预处理。将护坡上③预制块与①预制块间的相对角度α3和相对位移x3、y3作为输入层神经元参数,将待铺装的②预制块的与①预制块间的相对角度α2和相对位移x2、y2为输出层神经元参数,划分完数据集后对数据进行预处理。
(2)确定BP神经网络的拓扑结构和相关参数(神经网络的迭代次数、目标误差的阈值、学习率和适应度函数)。其中适应度函数fit(s,t)将输出值和预期值之间的差值的绝对值进行累积。
(7)
(3)将BP神经网络各层神经元的权值和阈值编码,组成遗传算法的种群,以BP神经网络根据不同种群的权值和阈值计算得出的输出值和期望值的误差带入适应度函数计算,通过滚球行为、繁殖行为、觅食行为、偷窃行为的算子,使得BP神经网络向误差更小的方向进化。
(4)将误差最小的BP神经网络的权值和阈值保留下来,作为BP神经网络的参数,将测试集数据输入检验神经网络的准确度,通过迭代次数、误差范围来评价神经网络。
2 实例应用
2.1 实验环境和参数
模型训练环境:处理器为Intel(R)Core(TM)i5-10200H CPU@2.40GHz,显卡为NVIDIA GeForce GTX1650,操作系统为Windows10,深度学习框架为Pytorch1.6.0,语言环境为python3.7,使用CUDA10.2和Cudnn7.6.5对GPU加速。部分试验参数如表1所示。
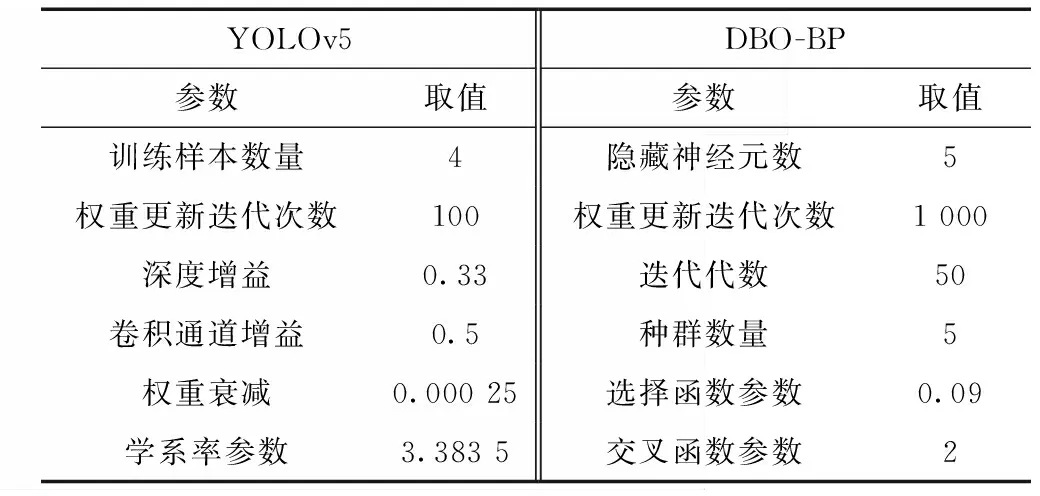
表1 试验参数
2.2 目标检测及定位抓取模型构建
采用现场实拍的方式收集了某渠道工程的预制块图像。经过筛选,选用100张1 920×1 440的预制块图像。通过开源标注工具LabelImg手工标注原始图像中的预制块,制作标签文件,得到的预制块目标分布和尺寸如图6所示。由图6a知,数据集的图像主要集中分布于0.25~0.45之间,目标长与宽基本一致。由图6b知,标签分布情况比较分散,在取得的彩色图中各个部分均有分布。
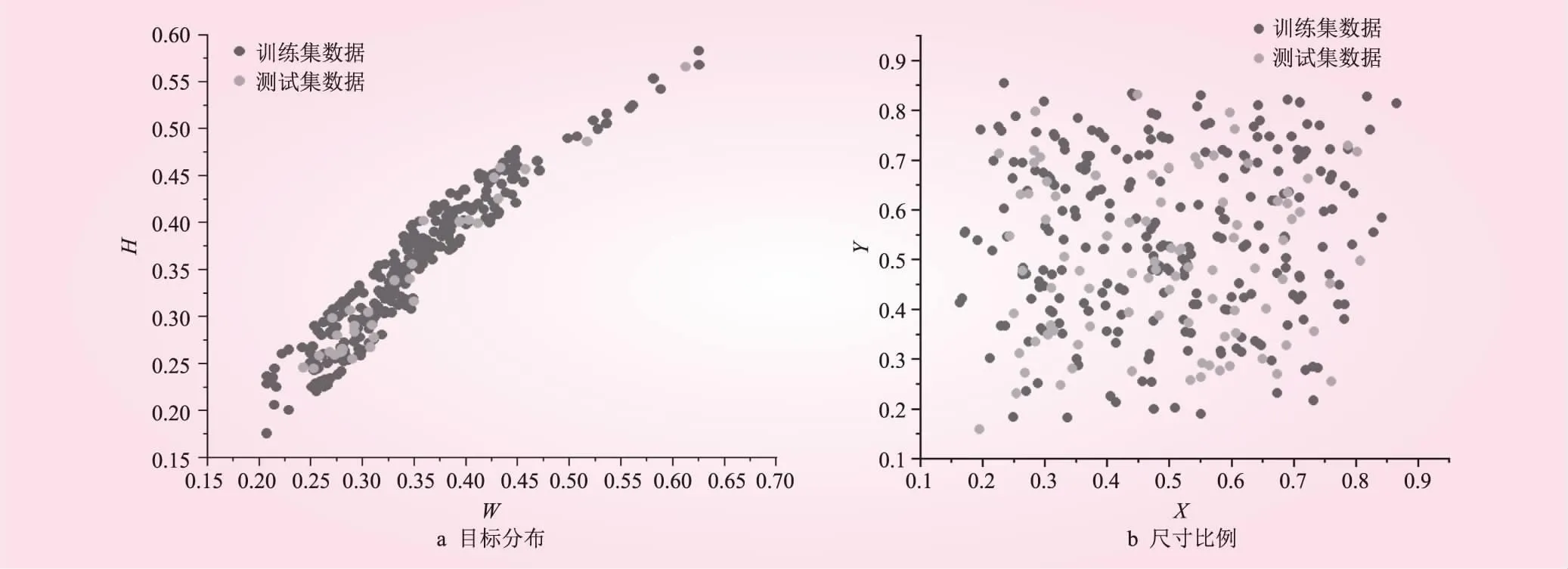
图6 预制块目标分布与尺寸
根据渠道现场实地测量,预制块的尺寸为l×l×h=615 mm×615 mm×120 mm,凹槽长56.75 mm,凸块长47.75 mm,凸块和凹槽斜边的角度相等,均为45°。为了便于试验验证,等比例缩放至1/4。根据公式l′=l×s可以计算出缩放后的预制块尺寸为153.75 mm×153.75 mm×30 mm,模型凹槽长14.19 mm,凸块长11.19 mm,凹槽深15.5 mm,凸块深14.5 mm。若预制块的中心位于坐标原点,预制块凹槽的限制范围表达如下
(8)
(9)
2.3 试验结果和分析
2.3.1 图像处理系统
2.3.1.1 目标检测算法
目标检测算法对图像的处理效果如图7所示,目标检测算法首先对原始彩色图进行预处理,再运行YOLOv5s_6模型,识别出预制块中心区域。将预制块中心区域的范围保存,用以分割点云图,定位预制块中心坐标。

图7 目标检测算法运行效果
目标检测算法运行效果如表2所示。表中,P为精确率;R为召回率;MAP_0.5指的是GIoU阈值取0.5时的均值平均精度MAP值,MAP_0.5-0.95指的是GIoU阈值取0.5~0.95、步长为0.05时的MAP值,使用权重大小作为模型是否轻量化易于工程部署的评价标准,使用训练时间和检测时间作为模型运行效率的评价标准。

表2 原始模型与改进后的模型性能比较
从表2可知,改进后的模型相较于原始模型,各参数都有一定程度的提升,增强了对预制块识别的精度。由于并未对模型结构进行调整,改进YOLOv5s模型较原模型迭代过程指标相近,精确率、召回率、MAP_0.5值和MAP_0.5-0.95值分别提高1.05%、2.2%、2.4%和2.03%;虽然模型大小略有增加(权重文件仅增加7KB),但模型效率能够有效提高,训练时间和检测时间分别减少0.051 h和0.043 s。
随着训练进行,训练的进行置信度损失值迅速下降并趋于稳定,精度不断增加,模型逐渐达到最优性能。原始模型与改进后的模型训练过程对比如图8所示。改进后的模型执行都损失值一直低于原始模型,MAP值在0~27次迭代波动较明显,且从第22次迭代开始一直高于原始模型。综上,在略微增加模型规模的前提下,可提高模型的识别精度和速度,满足预制块铺装高效率的要求。
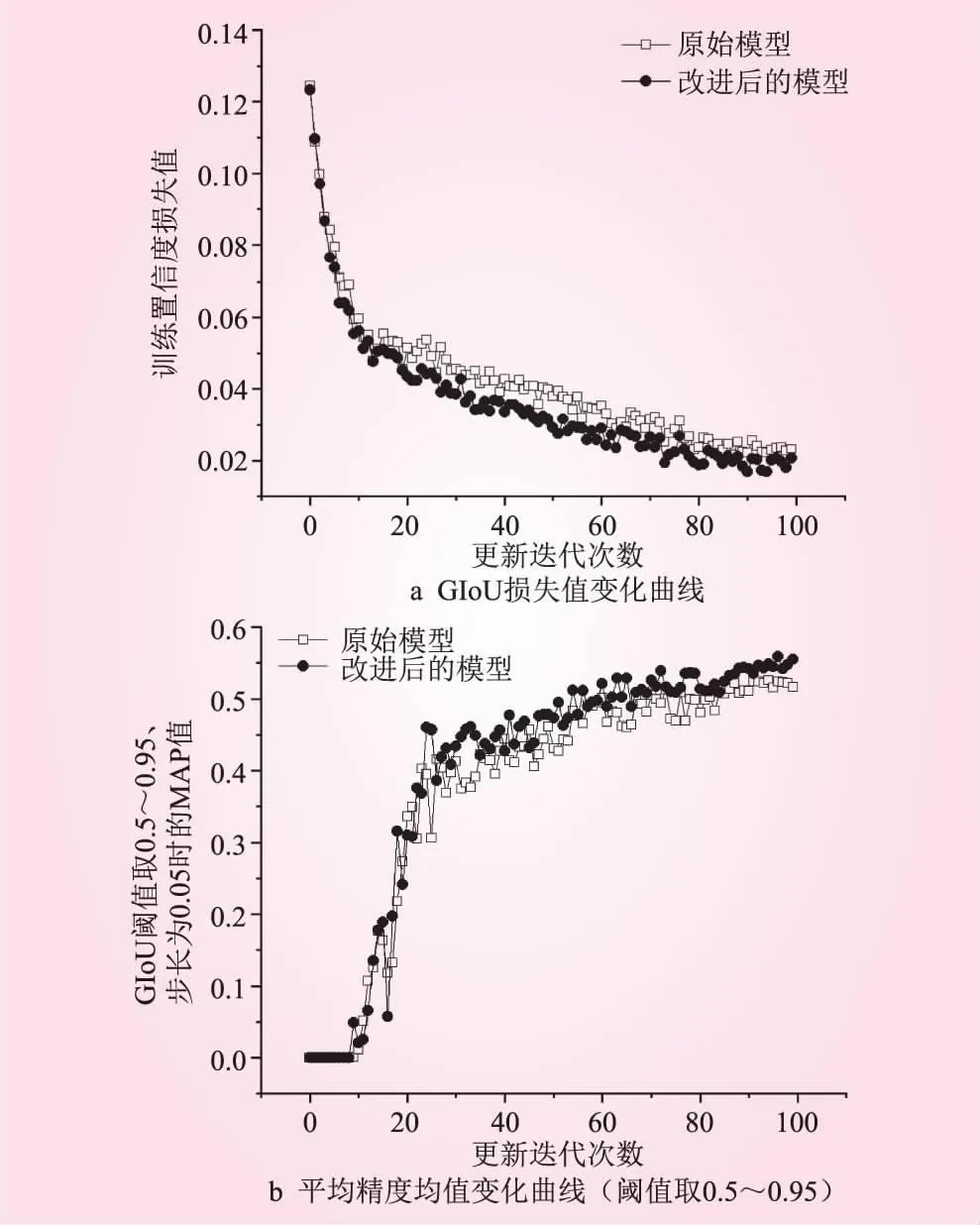
图8 原始模型与改进后模型训练过程对比
2.3.1.2 目标定位算法
根据预制块等比例缩放模型尺寸,使用3D打印技术制作模型,模拟铺装过程中渠道上预制块的摆放位置,结构光相机采集图像。图像经过目标检测算法处理,目标定位算法计算预制块中心和偏转角度,将计算数据与实际预制块的中心和偏转角度比较,以模拟现场铺装工况,以十字线确定预制块的中心位置,红点为定位计算系统的计算结果,试验如图9所示。经试验,目标定位算法的坐标定位和角度计算均与实际值偏差0.1 mm,达到预期效果。

图9 铺装图像采集模拟试验
2.3.2 定位计算系统
将遗传算法优化BP神经网络(GA-BP)[20]与蜣螂算法优化的神经网络(DBO-BP)比较。对GA-BP和DBO-BP使用相同的数据集和测试集进行训练和仿真预测,将1900个数据作为神经网络的训练集,将100个数据作为神经网络的测试集,分别导入DBO-BP神经网络和GA-BP神经网络,比较神经网络的性能。比较两种神经网络对数据输出在预测的准确性和训练过程中的收敛性能,结果见表3。表3中,MAE为平均绝对误差,MSE为均方误差。
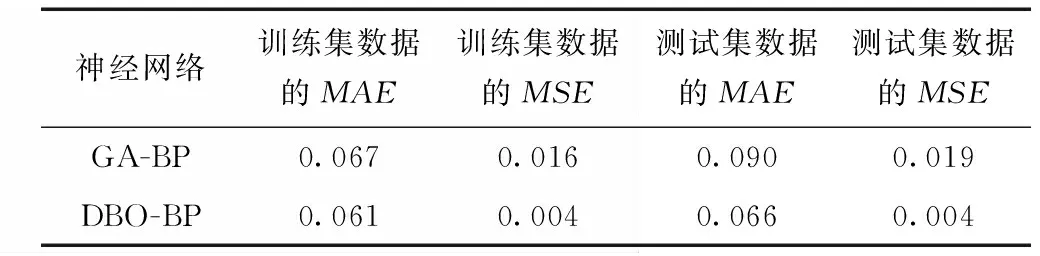
表3 GA-BP与DBO-BP性能比较
从表3可以看出,GA-BP的测试集数据比训练集数据高0.024,而DBO-BP的测试集数据比训练集数据高0.005;平均误差两者相差不大,因此DBO-BP的训练效果更好,对数据预测效果更精确。DBO-BP神经网络对训练集数据预测的平均绝对误差值和均方误差值均小于GA-BP,故使用DBO-BP,比GA-BP对预制块铺装所用的数据集有更好的适应性。
分别使用GA-BP和DBO-BP从数据集中挑选100组数据进行仿真模拟,模拟结果如图10所示。从图10可以看出,DBO-BP的最大预测误差百分值为0.134,最小预测误差百分值为0.001;GA-BP的总体预测效果误差较大,最大误差百分值为0.280,最小误差百分值为0.005。DBO-BP的预测误差百分值比GA-BP的预测误差百分值平均低0.056;在第99次仿真预测模拟,DBO-BP与GA-BP预测精度相差最大为0.220。试验结果表明,DBO-BP有更加良好的预测精度,且预测值与真实值误差较小,表明DBO-BP对铺装状况能够实时调整,预测出合理的预制块铺装位置。
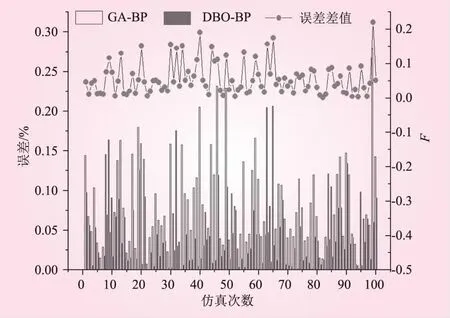
图10 神经网络仿真模拟结果
随着训练进行,目标函数值迅速下降并趋于稳定,精度不断增加,模型逐渐达到最优性能。GA-BP和DBO-BP模型训练过程对比如图11所示。从图11可知,DBO-BP的均方误差一直低于GA-BP;GA-BP的均方误差值初始值较高,在前9次迭代范围内,均方误差下降幅度较大,最佳性能状态为第53次,均方误差为0.019;DBO-BP的均方误差初始值较低,在前12次迭代范围内,均方误差变化幅度较小,最佳性能状态为第53次,均方误差为0.004。在前7次迭代,GA-BP与DBO-BP的误差差值在逐渐降低,在第8次至第10次迭代,GA-BP与DBO-BP,逐渐增大,在第10次迭代往后,GA-BP与DBO-BP的均方误差均在缓慢下降,DBO-BO的均方误差下降幅度略大。由此可知,遗传算法优化后的初始权重参数对神经网络的适应性不如蜣螂算法优化的权重参数。在进行7次神经网络迭代时,两者性能相近,随着迭代次数增加,DBO-BP提高模型准确度要比GA-BP高。
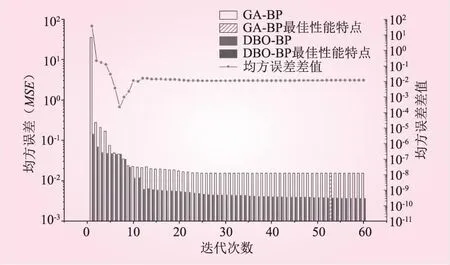
图11 神经网络均方误差变化结果
3 结 论
(1)本文通过图像预处理,优化YOLOv5模型,可以在一定程度上提高预制块的识别精度,同时能有效提升模型训练和目标检测的速度,减少训练和检测所用时间,对提高铺装工作效率有重要意义。
(2)将点云处理算法和目标检测算法相结合,为预制块铺装机械识别、定位预制块提供有效解决途径。对预制块的坐标计算效果良好,精度高,满足铺装要求。
(3)通过现场采集数据,建立数值模型,先进行数值模拟试验,获取试验数据后,使用蜣螂算法,实现输入预制块间的相对位移、旋转角度后输出预制块的铺装坐标。满足预制块铺装对铺装点较高精度计算的需要。
