基于改进物元分析法的疏勒河中上游生态流量计算与评价
2023-12-27闫宏华杨文举赵映东
闫宏华,杨文举,赵映东
(甘肃省水利厅讨赖河流域水资源利用中心,甘肃 酒泉 735000)
0 引 言
疏勒河干流发源于祁连山脉的岗格尔肖合力岭,与大通河、布哈河和黑河源头相邻,干流由东南向西北穿行于讨赖南山与疏勒南山之间,流域面积4.12万km2,干流全长670 km。疏勒河干流自上而下依次设定花儿地(1967年撤销)、昌马堡、潘家庄、双塔堡水库4个水文站,其中昌马堡水文站作为内陆河主要的大型水文站,承担着中央防汛办、甘肃省防办、酒泉市防办报汛的任务,为可持续的水文信息发挥着十分重要的作用[1]。
生态流量作为评价河流生态健康状况重要的水力学参数,反映了河流生态健康状况。目前国内外学者大多采用几种方法用来计算当地生态流量,而后通过综合分析指标进行当地最优生态流量的确定。李千珣等[2]基于4种生态流量计算方法计算清江生态流量过程,并采用Tennant法对结果进行合理性分析。崔静思等[3]基于5种水文学法和水力学法对梯级小水电应下泄的最小生态流量进行计算,分析对比发现Texas法和Tennant法更适合该地区最小生态流量计算。陈楷等[4]通过多种水文学法确定密江河生态流量值,并最终确定Tennant法最适用于当地生态流量计算。但是这些方法还存在机理识别不清、方法适用条件不明等问题,导致由此计算得出的生态流量无法满足水生生物健康发展的内在需求[5]。因此,有必要对目前常用的确定生态流量的水文学方法进行深入研究,探究一种综合客观分析方法明确水文学方法的适用性。
因此,本研究选取年内展布法、NGPRP法、最小生态流量法、逐月频率法及Tennant法5种计算方法对疏勒河干流中上游生态流量进行计算,基于博弈论确定综合权重的改进物元分析模型对生态流量计算结果进行评价,最终确定最适合疏勒河干流中上游生态流量,以期为计算河道生态流量过程提供新方法。
1 计算方法与原理
1.1 年内展布法
年内展布法以研究河道历史长系列径流资料为依据,引入多年平均流量和最小年平均流量的同期均值比η,通过此值同需要计算的河道生态流量建立联系,进而确定河段生态流量数值[6],计算步骤如下:
(1)依据长系列径流资料,求取多年平均流量Q和最小年均流量Qmin。
(2)求得多年平均流量和最小年平均流量的同期均值比η。
η=Qmin/Q
(1)
(3)最后利用同期均值比,确定河段生态流量的值Qi。
Qi=ηqi
(2)
式中,Qi为第i个月的生态流量,m3/s;qi为第i个月的多年平均流量。
1.2 NGPRP法
NGPRP法是将已知的长系列水文年分为丰水年、平水年和枯水年,以长系列水文年中的平水年为主要研究对象,对平水年进行排频,取90%保证率的年内各月径流量作为河段生态流量的计算方法[7]。
1.3 最小生态流量法
最小生态流量法以历史多年径流系列中各月的最小月平均流量作为该月的生态流量,组成最小生态流量过程[8]。
1.4 逐月频率法
逐月频率法根据具体河流的水文特征以及生态需求目标选取合理的保证率,得到适宜生态流量过程[9]。不同学者采用的保证率选取方法不同,本文采用3种选取方法进行计算,分别为:①取法I。枯水期保证率取90%、平水期保证率取70%、丰水期保证率取50%;②取法II。各月保证率均取50%;③取法III。冬季保证率取80%、春秋季保证率取75%、夏季保证率取50%。计算各种方法的流量,得到适宜生态流量过程。
1.5 Tennant法
Tennant法也叫蒙大拿法,普遍用于估算河道生态基流或生态需水量[10-11]。Tennant法将雨季和旱季的河流流量与鱼类栖息地质量联系起来,并量化为年均流量的百分比;引入10%作为最小瞬时流量,30%被推荐为基本流量,60%为最佳瞬时流量。基于河流测站的观测数据,确定了年平均流量的各种百分比,进而提出了河流生态流量的标准[12]。
2 改进物元分析法生态流量过程评价模型
2.1 建模过程
物元分析法是以相关的数学理论为基础,利用实地监测的水文径流数据,构建模糊评价模型,再利用构建的模糊评价模型合理、正确的分析与评价研究对象[13]。因此,本研究将物元分析法的思路应用到河道生态流量过程中。其建模过程为:①利用实地监测的12个月河道生态流量数据,作为整个生态流量过程的衡量评价指标;②借鉴传统水文学计算方法中的Tennant法的评判准则,构建评价模型的经典域和节域;③利用实地监测的12个月生态流量满足度的重要性,基于博弈论思想确定12个月的权重;④通过利用上述步骤确定各方法评价等级的综合关联度;⑤通过确定利用各种计算方法对生态流量过程结果的整体评估等级,从而最终确定合理的生态流量过程。
2.2 评价标准的确定
Tennant法是水文学计算方法中常见的方法,当用于实际生态流量确定时,应当针对河道所处的地理位置状况、河流的水文情势以及河流生态需水量状况等,做出适当的分期和标准参数调节。考虑到疏勒河流量具有明显的季节性变化,为弥补Tennant法不适用流量季节性变化大的不足,使模型评价结论更为精确,因此,将一年分为丰水期、平水期和枯水期不同时段。其具体的界定方式是:将全年区分为丰水期、平水期与枯水期,参考已有经验与疏勒河流量特点,划定4月~6月为平水期,7月~10月为丰水期,11月~3月为枯水期[14]。
2.3 基于博弈论的改进物元分析法评价模型
2.3.1 构建待评物元与关联函数
将疏勒河干流中上游12个月的生态流量状况作为评价指标体系,记为12个特征,并建立物元,即
(3)
式中,n为12;Pn为生态流量过程;Ci为第i个月的生态流量状况;Xi为第i个月生态流量占多年平均流量的百分比。
依据相对应的评价等级标准,本文参考黄显峰等[15]的研究结果,构建模糊评价模型的经典域和节域这两个域的物元,并确定关联度与关联函数,计算公式为
(4)
式中,Xji为待评对象的第i个指标的经典域,|Xji|=api-bpi;Kj(xi)为目标层的综合关联度;ρ(xi,Xji)为分辨系数;Xpi为待评对象的第i个指标的节域;api、bpi分别为第i个评价指标对应等级a与等级b的量值范围。
2.3.2 基于层次分析法确定主观权重
层次分析法(AHP法)是一种采用定性和定量分析解决复杂多层次、多目标的分析决策方法[16],其计算过程如下:
(1)目标递阶层次结构评价模型和判断(成对比较)矩阵的建立。首先把决策问题层次化、模块化,即依次按照目标层、准则层和方案层分组建立一个目标递阶层次结构评价模型。基于上述评价模型,两两比较,构建判断矩阵,即
S-Bm=(bmn)k×k
(5)
式中,S为元素a的重要性程度;Bm为元素b的重要性程度;bmn为评分结果,bmn>0,bmn=1/bnm,bmm=1;k为判断矩阵阶数。当元素进行两两比较时,标度法的范围为1~9。
(2)目标元素相对权重的计算。通常采用求特征值λ法和一致性指标WAj来确定相应的特征向量I,则一致性指标WAj与特征值λ计算方法为
(6)
(7)
式中,W为权重;Wm为判断矩阵m行权重;WAj为一致性指标,I=(WA1,WA2,…,WAj);m为判断矩阵行数,m=1,…,i;n为判断矩阵列数,n=1,…,j。
2.3.3 基于熵权法确定客观权重
熵权法是根据某项指标信息熵的定义,熵值的大小可以用来判断指标的离散程度[17],离散程度越大,熵值(权重)就越小;相反,熵值(权重)就越大,其计算过程如下:
(1)数据的标准化处理。假设已知有i个指标X1,X2,…,Xi,每个指标有j期数据,可构建一个i行j列矩阵。数据标准化处理公式为
(8)
式中,Yij为指标标准化处理后参数;Xij为第i个指标的第j期数据;Xi为第i指标的所有数据(i=1,…,m;j=1,…,n)。
(2)确定各指标信息(熵)权重。依据上述信息熵的定义,先计算出各指标信息熵的大小,然后通过信息熵确定出各指标的(熵)权值。信息熵和权重确定公式为
(9)
(10)
(11)
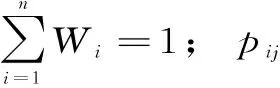
2.3.4 基于博弈论确定组合权重
主观赋权法决策者主观偏好较强,客观赋权法又过多依赖于实测数据的局限性,为综合考虑决策者的主观偏好信息、实测数据的对比强度与冲突性,因此,基于博弈论对AHP-熵权法主客观赋权结果进行组合赋权,得到决策者客观可信的评价结果。根据上述层次分析法与熵权法确定的各指标权值WA和Wa,得到两个权重向量u1和u2,基于博弈论组合模型[18],推求契合度最高的权重向量u*,计算公式为
(12)
式中,a=1,2;ka为最优的线性组合系数。
2.3.5 计算第j个评价等级的联合关联度
(13)
式中,ui为第i个月生态流量状况的权重;Kj(P0)为联合关联度;Kj(xi)为关联函数,代表物元达到所规定的取值范畴的程度。
2.3.6 确定等级评定
若Kj=max{Kj(P0)}(j=1,2,…,m),则表示所确定的生态流量过程已达到了第j级别。处于Kj(P0)≤-1范围时,表明认为不满足该标准级别的条件,并无法转换为该级别;处于-1
2.3.7 确定生态流量过程
通过按照所选用的各种生态流量确定方法,确定了各种计算方法的生态流量过程评价等级,并结合所调查的疏勒河干流中上游生态用水要求,合理地确定出所求的生态流量过程。
3 疏勒河干流中上游生态流量计算与评价
3.1 生态流量过程计算
采用传统水文计算方法中的年内展布法、NGPRP法、逐月最小流量法、逐月频率法,利用疏勒河干流中上游昌马堡水文站1953年~2017年的径流资料,计算所求的生态流量过程,不同方法的各月生态流量结果如表1所示。
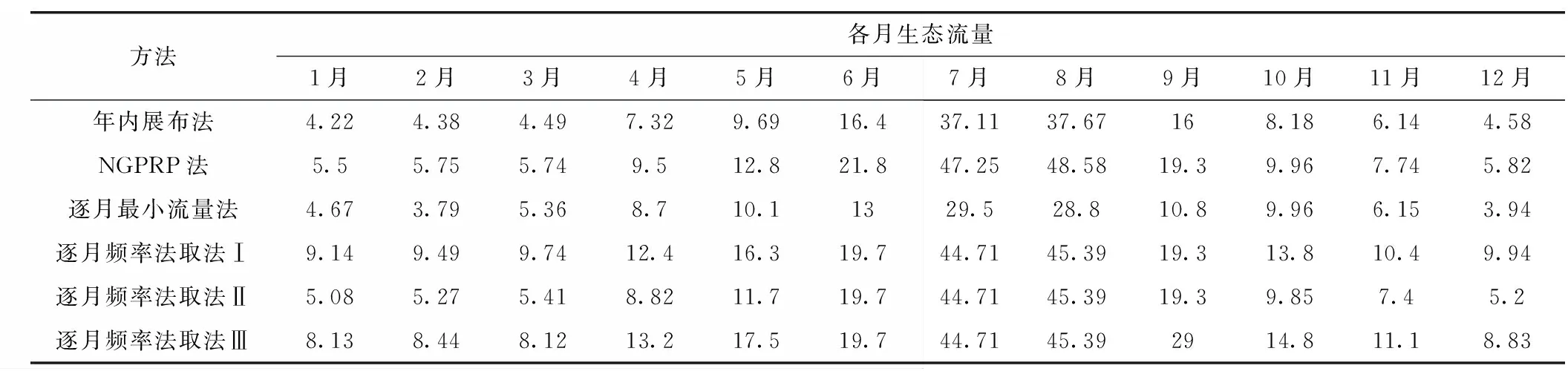
表1 采用不同生态流量计算方法确定的各月生态流量计算结果 m3/s
由表1可知,疏勒河干流中上游生态流量计算中不同方法的计算结果差距较小,各月生态流量值基于不同方法下变化不大,无法直观看出各方法结果的差距,具体评价需要采用生态流量评价模型。
3.2 基于改进物元分析法的生态流量过程评价
依据疏勒河干流中上游的生态环境现状情况以及生态流量下泄的要求,同时考虑疏勒河干流中上游所在流域降雨的特点,全年的生态流量重要性概况为:丰水期<平水期<枯水期。丰水期这一时段的重要性最低,枯水期这一时段的重要性最高。根据层次分析法与熵权法的基本过程,对疏勒河干流中上游各月生态流量进行赋权处理,采用博弈论组合赋权方法计算得到各月生态流量的组合权重,具体见表2。

表2 生态流量赋权结果
以传统水文计算方法中的逐月最小流量法为例,根据所求生态流量过程的评价等级相关标准要求(见表3),构建待评物元R、经典域物元Rj(j=1,2,…,7)。生态流量过程的评价等级分为7个等级,分别为差、一般、较好、好、很好、最佳、最大,结果见表4。考虑权重关系后,再按照公式(13)计算各评价等级之间的综合关联度,差、一般、较好、好、很好、最佳、最大的综合关联度分别为-0.333、-1.03、-1.04、-1.031、-1.024、-1.017、-1.011。
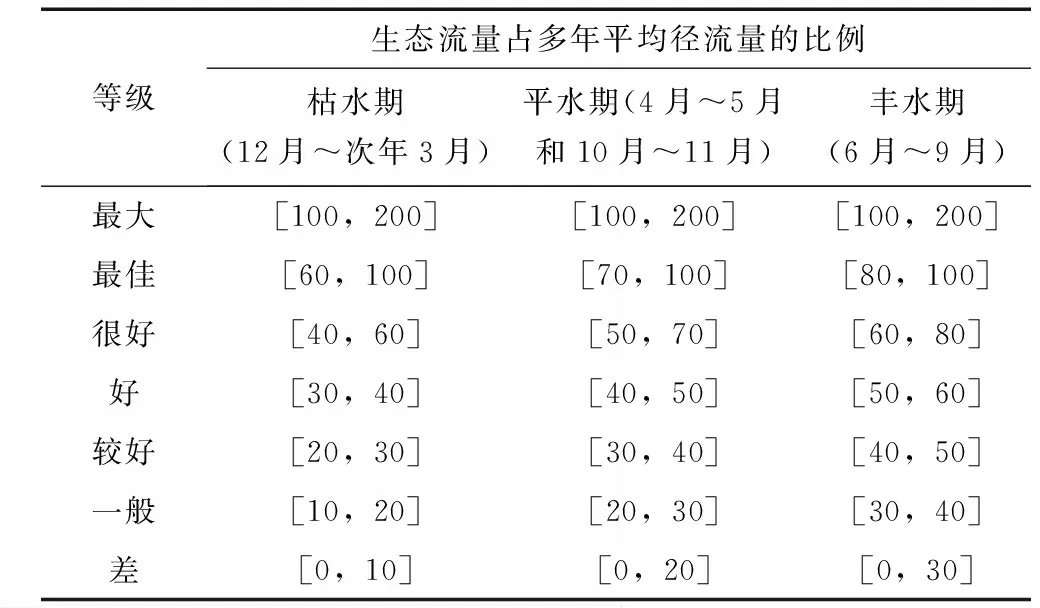
表3 河流生态流量过程评价标准 %
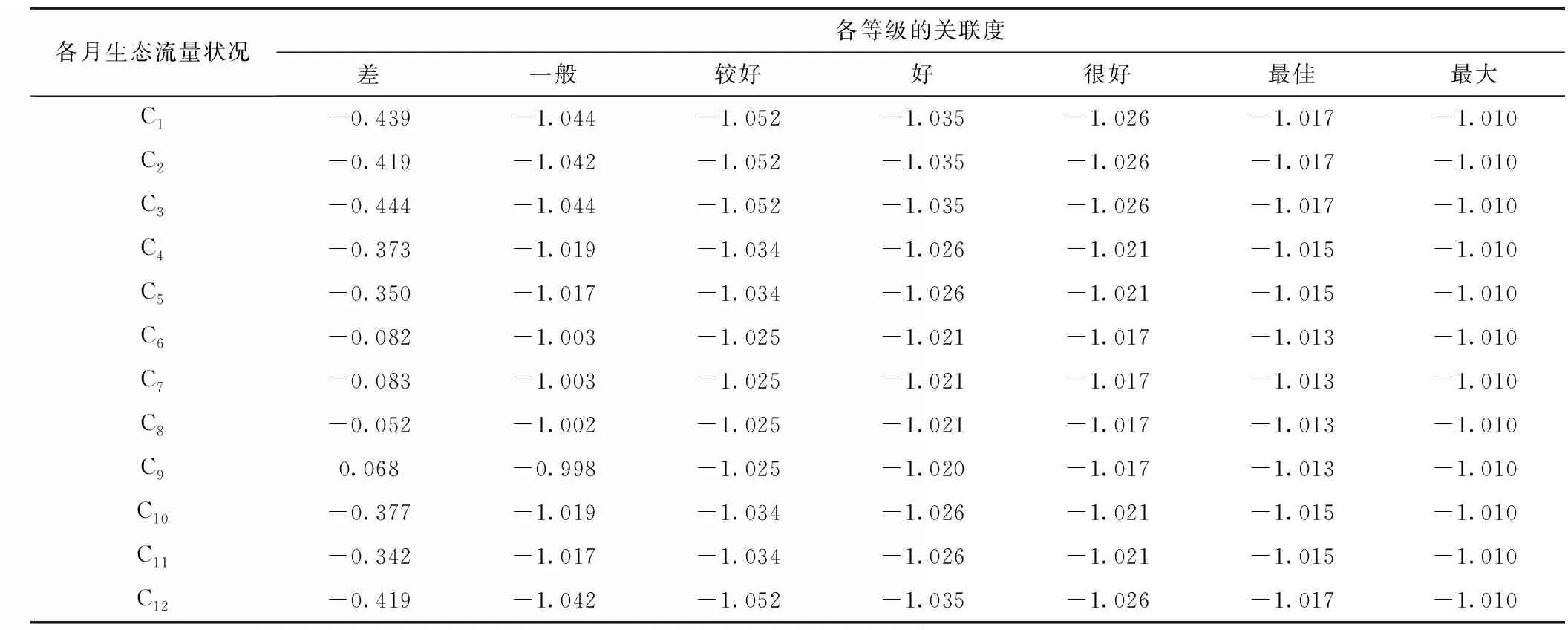
表4 各评价等级的综合关联度
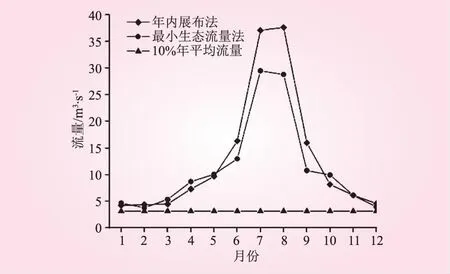
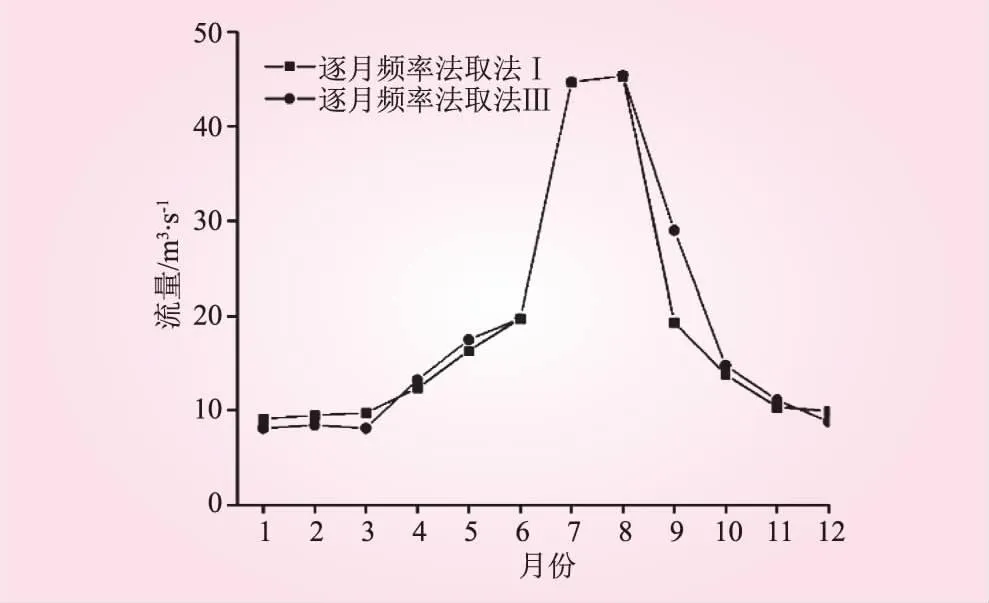
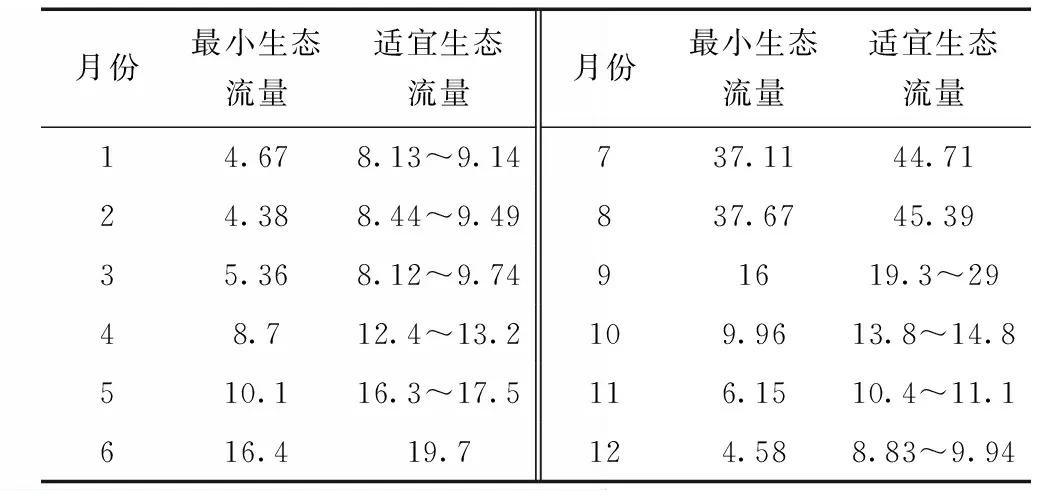
由表4可知,当Kj=max{Kj(P0)}(j=1,2,…,7)=-0.333时,由传统水文计算方法中的逐月最小流量法,所求得的生态流量过程评价等级为差。且Kj处于-1 表5 不同生态流量计算方法确定的生态流量过程评价结果 由表5可知,采用传统水文计算方法中的各生态流量计算方法,来确定河道的最小生态流量过程时,年内展布法计算结果评价等级为“好”,而最小生态流量法的计算结果评价等级为“差”。最小生态流量过程按照相对应的评价标准,评价等级确定为“好”的生态流量过程,其最小生态流量宜按照多年平均流量的30%~60%确定;评价等级确定为“差”的生态流量过程,其最小生态流量宜按照多年平均流量的0~30%确定。Tennant法认为10%的流量是为防止生态退化的最小流量,可以满足河道内各种水生生物和植物的最低生存要求。为了流域生态系统的长足发展,应在确定的河道最小生态流量过程的基础上预留一定的空间。因此,取评价等级为“好”的年内展布法和评价等级为“差”的最小生态流量法计算结果进行耦合,取其外包线作为最小生态流量过程,且不低于10%的多年平均流量,如图1所示。 图1 最小生态流量过程耦合 对于短期的河道水文情势而言,确定的河道最小生态流量过程可以满足河流生态系统稳定的要求。为了保持河道生态系统的可持续发展,对于长期的河道水文情势而言,还应确定适宜生态流量过程。 综合上述分析,利用所选取传统水文计算方法中的各生态流量计算方法,来确定适宜生态流量过程时,采用NGPRP法和逐月频率法取法Ⅱ确定的生态流量过程评价等级为“很好”,采用逐月频率法取法Ⅰ与逐月频率法取法Ⅲ确定的生态流量过程评价等级为“最佳”。按照相对应的适宜生态流量过程的评价标准,确定的生态流量过程评价等级为“很好”的,适宜生态流量按照多年平均流量的40%~80%计算;确定的生态流量过程评价等级为“最佳”的,适宜生态流量按照多年平均流量的为60%~100%计算。由于干流中上游保护对象为湿地生态系统[19],为保证下游河道内水生生物的生存和水生态系统的平衡,同时考虑到60%~100%的年平均流量为最适宜的生态流量[15],因此,采用逐月频率法取法Ⅰ与逐月频率法取法Ⅲ计算结果进行耦合,取其外包线和内包线分别作为适宜生态流量过程阈值的上下限,如图2所示。由于昌马堡水文站上游距离不远处有月儿弯一级水电站,承担着重要的发电任务,因此,结合上游来水及发电需求,在适宜生态流量阈值内灵活泄放生态流量,可以最大限度的提高水资源利用率。 图2 适宜生态流量过程耦合 由图1、图2分析得出各月最小生态流量和适宜生态流量,如表6所示。 表6 生态流量过程 m3/s 由表6可知,最小和适宜生态流量过程变化趋势都呈现出先增大后减小的变化趋势,即从1月份开始,逐渐增大,到8月份时,达到最大值,而后直到12月份,又开始持续减小。二者变化趋势均呈现先增后减的变化趋势,与实测资料相符,其结果可靠。 (1)采用年内展布法与逐月最小流量法确定的疏勒河干流中上游最小生态流量过程,以及采用逐月频率法取法Ⅰ与逐月频率法取法Ⅲ确定的疏勒河干流中上游适宜生态流量过程符合该流域的生态水文特征,以期为疏勒河干流中上游生态修复提供科学参考。 (2)本文基于博弈论思想提出改进物元分析法的河流生态流量过程综合评价模型,并应用于疏勒河干流中上游生态流量计算,模型适用性较高。研究可为推求河道生态流量分析确定提供新方法。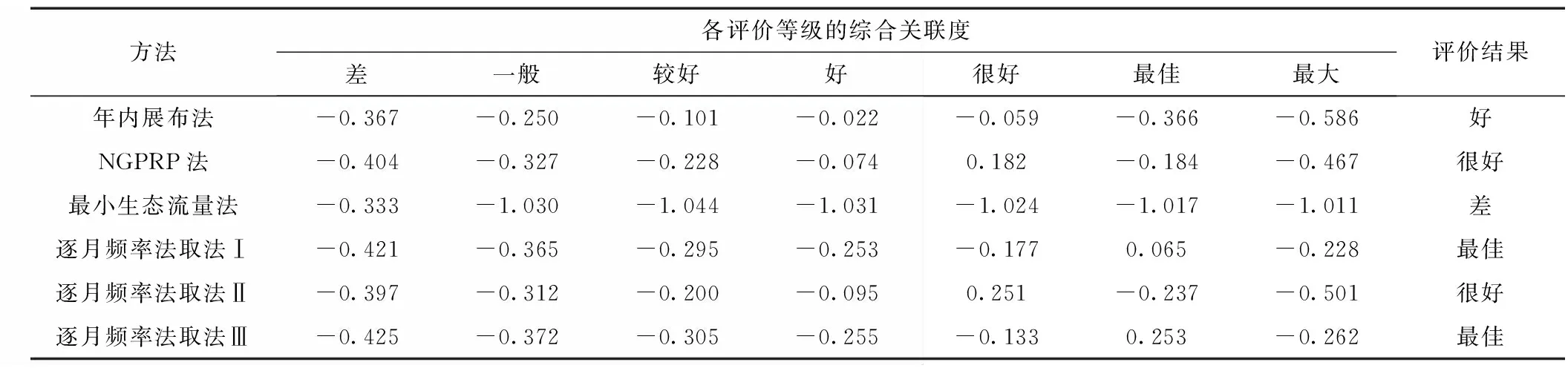
3.3 评价结果分析
4 结 论
