太行山典型油松林降雨再分配规律*

2023-12-27李佳聪朱春雨赵宇寒曹建生沈彦俊

中国生态农业学报(中英文) 2023年12期

郭波,阳辉,李佳聪,朱春雨,赵宇寒,曹建生**,沈彦俊**

(1.中国科学院遗传与发育生物学研究所农业资源研究中心/中国科学院农业水资源重点实验室石家庄 050022;2.中国科学院大学现代农业科学学院北京 100049)

华北地区河川径流衰减及地下水位下降引发了一系列生态环境问题,如地下水漏斗、地面沉降、海水入侵等[1]。太行山位于海河流域上游,是华北平原60%以上河流的发源地[2-3],是华北平原重要的生态屏障区[4]。太行山区作为水资源涵养区和形成区,是平原区水分补给的来源,随着“太行山绿化工程”等的实施,山区植被不断恢复[3-4]。长期植被恢复对区域水循环产生影响,在有限的降雨条件下,植被恢复增加了蒸散量,区域产水量减少[5],这对下游城市供水产生了影响。林冠层对降雨起到再分配作用,降雨经过林冠后被分配为林冠截留、穿透雨、树干径流,降雨再分配过程具有重要的生态水文学意义,如林冠截留会影响后续的水文过程。因此需量化森林生态系统降雨再分配要素,这对区域产水量及水资源量的评估尤为重要[6-7]。

林冠截留是指降雨后被叶片或枝条表面截留的降雨[8],是森林生态系统水循环的一个重要组成部分,也是水文模型的一个关键变量[9],研究表明中国不同森林林冠截留率为16.4%～28.8%[10]。目前,实地观测和模型模拟是定量降雨再分配要素的两种主要方法,实地观测有间接测量法(水量平衡法)和直接测量法(称重法),各方法均存在不完善之处。水量平衡法通过测定穿透雨量及树干径流量来计算林冠截留量,但林冠结构存在空间异质性,林冠下特定位置监测的穿透雨会存在大于降雨量的情况[7],因此需布设大量的雨量筒进行观测;直接称重法则需要将植物剪下称重,但在称重过程中很难保证水分不掉落,导致测定的截留量偏小[11]。模型模拟方法主要使用经验模型、半机理模型[8]对模型参数进行本地化。经验模型是基于野外实测数据,利用数理统计方法,得到截留量与总降雨量的关系,最后推求特定树种、特定降雨量下的截留量,经验模型忽略了截留的动力学过程,并没有考虑到林型与降雨特征[8,12]。半机理模型包括Rutter 模型[13]、Gash 模型[14]、Liu 模型[15]等。Rutter 模型考虑到了降雨特征,但模型所需参数较多,需小时尺度的降雨数据[13],且计算过程较为复杂,在实际应用过程中受到了限制[14];Liu[15]开发出一种无经验参数的截留模型,模型参数包括冠层盖度、林冠蒸发率、冠层干燥指数,且原始的Liu 模型在20 多种森林类型下均得到了很好的应用[16],之后Carlyle-Moses 等[17]将冠层盖度引入Liu 模型;原始的Gash 模型是Rutter 模型的发展,其简化了数据的输入,引入了线性回归方程[14],之后Gash 等[18]将冠层盖度引入模型,结果表明修正的Gash 模型较原始Gash 模型精度更高,所需参数较少,且在不同植被类型下均得到了很好的应用。不同区域水热条件、森林冠层结构等不同,模型参数也存在差异,在不同林型的应用效果也不同。Shi 等[19]将修正的Gash 模型应用到华山松(Pinus armandii)林中,结果表明修正的Gash 模型低估了截留量的5.87%;Su 等[13]研究表明修正的Gash 模型高估了截留量的6.2%;Yang 等[20]将Liu 模型及Gash 模型应用到青海云杉(Picea crassifolia)样地,结果表明Liu 模型较Gash 模型模拟效果更好。总体来看,当前研究对太行山区油松(Pinus tabulaeformis)林冠截留模拟的研究较少,需综合评估修正的Gash 模型及修正的Liu 模型在该地区的适用性。

太行山是黄土高原和华北平原的分界线,该区有着独特的气候条件,为半湿润区与半干旱区的过渡带,降雨量较少,植被较为茂盛,植被截留量对于流域水量平衡计算有重要意义[11]。因此,需量化太行山区典型油松林降雨再分配规律,得出适用于该地林冠截留模拟的参数。本文以太行山典型油松林为研究对象,阐明油松林降雨再分配规律,并基于实测数据评价修正的Gash 模型和修正的Liu 模型在油松林的适用性,为水资源管理、山区水源涵养能力提升提供理论依据。

1 材料与方法

1.1 研究区概况

本研究在中国科学院太行山山地生态系统试验站骆驼安试验点(113°51′55″E,38°40′6″N)开展,试验点海拔为1250 m,气候为温带大陆性季风气候,多年平均气温为10.6 ℃,多年平均降水量为573 mm,且降水主要集中在6−8 月。试验点所在小流域为柳林河流域,位于滹沱河流域山区。柳林河流域内主要乔木为油松、刺槐(Robinia pseudoacacia),灌木主要以荆条(Vitex negundo noronhavar.heterophylla)、绣线菊(Spiraea salicifolia)为主。流域内主要土壤类型为高活性淋溶土和疏松岩性土。

1.2 样地布设

在对柳林河流域植被进行调查的基础上,在流域上游选取一块典型油松样地,面积为400 m2(20 m×20 m),坡度为25°,林龄为30 a,样地密度为1700株·hm−2。对样地内胸径>5 cm 的乔木每木检尺,油松平均树高为9.4 m,平均胸径为17.6 cm。冠层郁闭度通过使用鱼眼相机在每个穿透雨收集器上部对林冠进行拍摄,拍摄过程中注意使相机保持水平,使用CAN-EYE V6.4.7 软件进行图像处理,最终确定样地郁闭度为0.7。

1.3 数据测定

在样地附近空旷处安装林外气象站,监测降雨量、气温、大气压、太阳辐射等,同时在自动气象站附近放置3 个标准雨量筒人工监测降雨量,对雨量计数据进行校正,保证林外降雨量数据的准确性。降雨事件划分标准会影响林冠截留量,为保证林冠截留量计算的准确性,每次降雨前林冠为干燥状态,以8 h 作为降雨事件的划分标准[13]。

样地内布置3 个自制的穿透雨收集装置(2 m×0.2 m)监测穿透雨量,考虑到穿透雨的空间异质性,随机布置21 个穿透雨收集器(直径为18 cm),为减少蒸发的影响,降雨后2 h 内测定穿透雨量。利用式(1)计算穿透雨量:

式中: TF 为穿透雨量,mm; TFi为第i个穿透雨收集器中穿透雨体积,mm3;Ai为第i个穿透雨收集器的受雨面积,mm2;n为穿透雨收集器的数量。

样地内选择8 个标准木测定树干径流,在树干高1.3 m 处将聚乙烯软管螺旋缠绕在树干上,铁钉固定软管,利用玻璃胶密封软管与树干的空隙。每次降雨后测定树干径流量,利用公式(2)将单株树干径流量转换为样地尺度的树干径流量[21]。

式中:S为树干径流量,mm;N为样地中树木总棵数;Sa为几个标准木的平均树干径流量,mL;A为样地面积,m2。

林冠截留量利用水量平衡公式[即式(3)]计算:

式中:I为林冠截留量,mm;P为降雨量,mm;T为穿透雨量,mm。

1.4 修正的Gash 模型

修正的Gash 模型将降雨事件划分为林冠加湿、林冠饱和、降雨停止后林冠干燥3 个阶段[18,22],林冠截留量(I)的计算公式为:

式(4)中各部分参数说明及计算方法见表1。

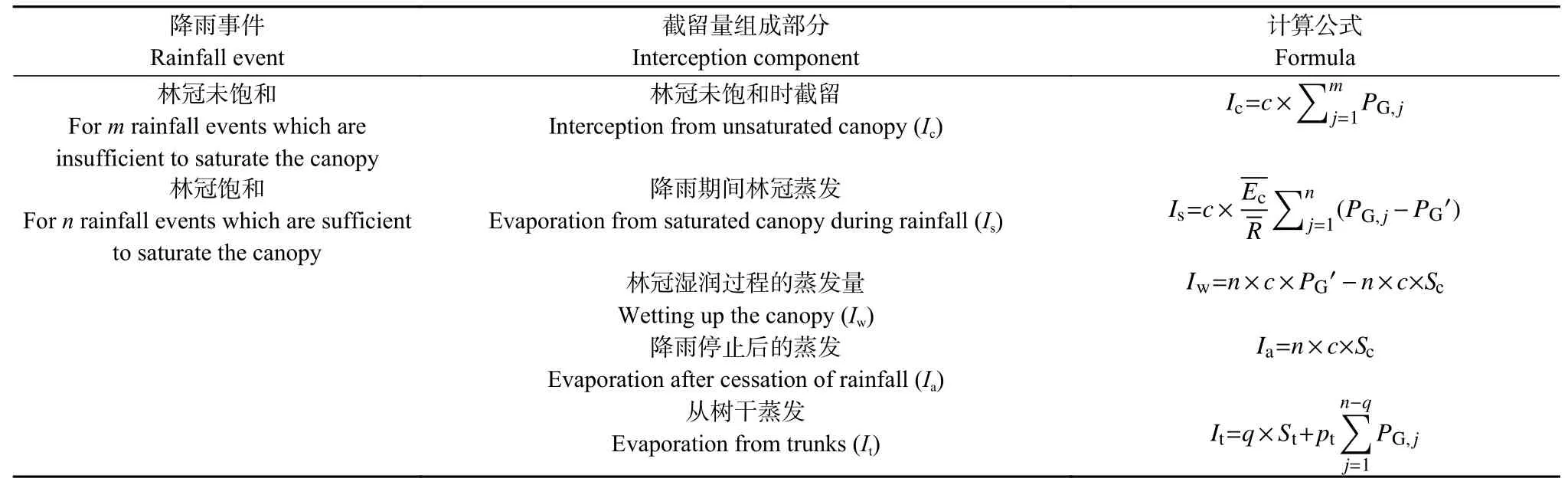
表1 修正的Gash 模型公式中各参数(截留量组成部分)的意义及计算公式Table 1 Meaning and calculation formula of each parameter (interception component) of the revised Gash model formula

利用修正的Gash 模型计算树干径流量和穿透雨量的公式如下:

式中: SFj为第j次降雨的树干径流模拟值;ptc为单位冠层面积的树干径流系数,通过树干径流系数除郁闭度得到[9];Stc为单位冠层面积的树干持水能力[13];式中其他参数见表1。

式中: TFj为第j次降雨的穿透雨模拟值; GRj为第j次降雨的降雨量;Ij为第j次降雨的林冠截留量;式中其他参数见表1。

使林冠达到饱和的降雨量(PG′)计算公式如下:

式中参数见表1。

使树干达到饱和的降雨量(GRt)计算公式如下:

式中参数见表1。

式中:a为截留量与总降雨量线性方程的斜率[13,23],式中其他参数见表1。

1.5 修正的Liu 模型

原始的Liu 模型[15-16]将林冠截留量定义为样地持水能力与降雨期间林冠蒸发量之和。Carlyle-Moses 等[24]将冠层盖度引入Liu 模型,公式如下:

式中:Cmc为单位冠层面积林冠及树干持水能力,即单位冠层面积的林冠持水能力和单位冠层面积的树干持水能力之和。

1.6 模型评价标准

使用实测值与模拟值线性方程的R2和相对误差评价模型的适用性。根据Muzylo 等[8]的研究,设定模型效果的评价标准如下: 非常好(相对误差≤1%)、很好(1%<相对误差≤5%)、良好(5%<相对误差≤10%)、一般(10%<相对误差≤30%)、较差(相对误差>30%)。文中线性、非线性拟合及作图使用Origin 2021 软件。

2 结果与分析

2.1 降雨量特征

2022 年7−11 月降雨次数为26 次,总降雨量为450.8 mm,平均次降雨量为17.3 mm,最大降雨量为102.8 mm,最小降雨量为1.1 mm (图1a)。26 场降雨的平均降雨历时10.4 h,平均降雨强度为2.7 mm∙h−1(图1a)。

景德镇的陶瓷美术作品主要属具象美术和意象美术范畴：工笔人物、山水、花鸟属具象美术，写意人物、山水、花鸟属意象美术。自宋元以来，在中国画的影响下，景德镇陶瓷美术中之具象美术与意象美术都得到了发展，只不过各有其特殊的领域。

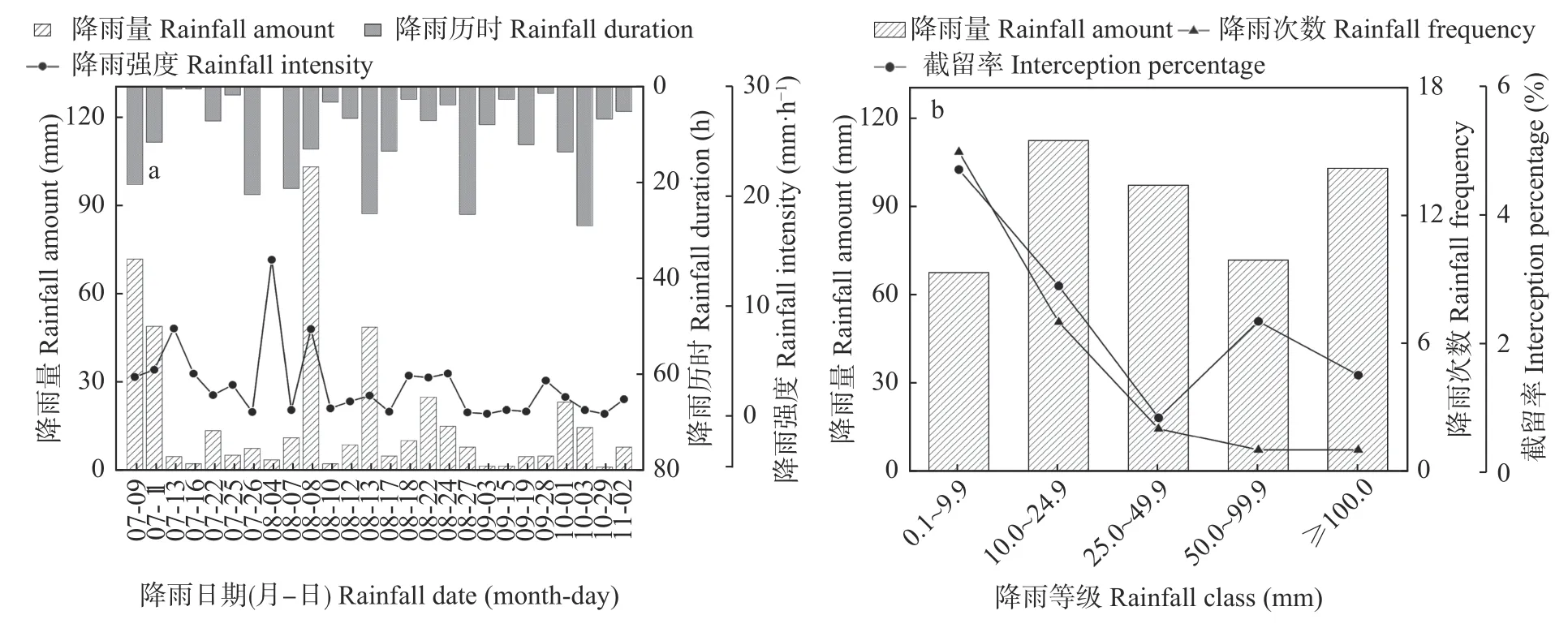
图1 试验期间研究区降雨特征Fig.1 Rainfall event characteristics during the study period in the study area

根据国标GB/T 28592−2012 中降雨等级划分标准,将降雨量划分为不同等级,其中0.1～9.9 mm 为小雨,10.0～24.9 mm 为中雨、25.0～49.9 mm 为大雨、50.0～99.9 mm 为暴雨、100.0～249.9 mm 为大暴雨。研究期间小雨15 次,占总降雨次数的57.7%,总降雨量为67.4 mm;中雨7 次,占总降雨次数的26.9%,总降雨量为112.1 mm;大于25 mm 的降雨4 次,占总降雨次数的15.4%,总降雨量271.4 mm (图1b)。

2.2 降雨再分配规律

2.2.1 穿透雨

试验期间共26 次降雨,22 次降雨产生穿透雨,穿透雨总量为338.2 mm,占总降雨量的75.0%;次降雨穿透雨率为11.9%～94.3%,降雨量与穿透雨量呈显著的线性关系(P<0.001),随降雨量的增加,穿透雨量呈增加趋势(图2a)。由方程可知,产生穿透雨量的阈值为1.7 mm。降雨量与穿透雨率呈幂函数关系,在降雨量较小时穿透雨率增加较快,当降雨量达到11 mm 时,穿透雨率的增加速度变慢(图2b)。

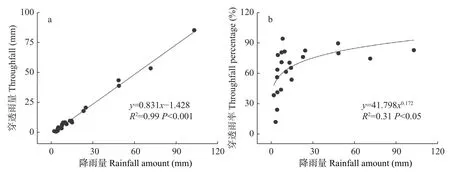
图2 林外降雨量与穿透雨的关系Fig.2 Relationship between rainfall and throughfall

2.2.2 树干径流

试验期间共26 次降雨,其中20 次降雨产生树干径流,树干径流总量7.1 mm,占总降雨量的1.6%。降雨量和树干径流量呈线性关系(P<0.001),随着降雨量的增加树干径流量呈增加的趋势(图3a)。由线性方程可知,当降雨量达到5.5 mm 时开始产生树干径流。降雨量与树干径流率为对数函数关系,在降雨量较小时树干径流率增加较快,当降雨量大于15 mm时,树干径流率增加速度变慢(图3b)。

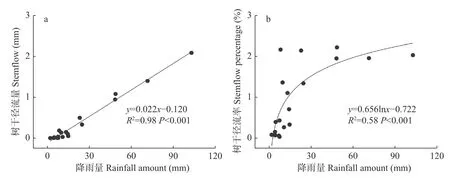
图3 林外降雨量与树干径流的关系Fig.3 Relationship between rainfall and stemflow

2.2.3 林冠截留特征

试验期间林冠截留总量为105.5 mm,占总降雨量的23.4%。降雨量与林冠截留量呈幂函数关系(P<0.001)(图4a),其指数为正。降雨量与林冠截留率也为幂函数关系,但其指数为负,即随着降雨量增加林冠截留率降低。在降雨初期林冠未饱和,截留率较高,当降雨量达到11 mm 时,林冠截留率明显降低(图4b)。

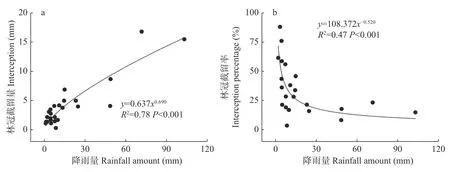
图4 林外降雨量与林冠截留的关系Fig.4 Relationship between rainfall and interception

2.3 截留模型参数确定及模拟结果

2.3.1 修正的Gash 模型及Liu 模型参数的确定

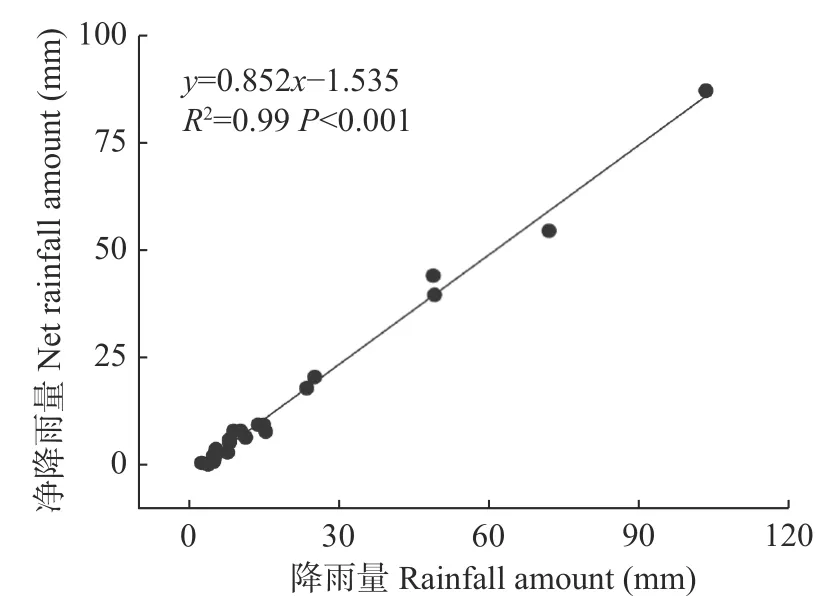
图5 降雨量与净降雨的关系Fig.5 The relationship between rainfall and net rainfall

表2 修正的Gash 模型及Liu 模型参数Table 2 Parameters of revised Gash model and Liu model

2.3.2 截留模拟结果

基于修正的Gash 模型计算得到林冠截留量、穿透雨量、树干径流量模拟值分别为105.3 mm、340.7 mm、4.6 mm。林冠截留量实际观测值为105.5 mm,模拟值和实测值相差0.2 mm,相对误差为0.2%;穿透雨量实测值为338.2 mm,模拟值和实测值相差2.5 mm,相对误差为0.8%;树干径流实测值为7.1 mm,与模拟值相差2.5 mm,相对误差为34.7%(表3)。修正的Gash 模型模拟的各部分截留量见表3,其中降雨期间林冠蒸发量为57.9 mm,占林冠截留模拟值的55.0%;降雨停止后林冠蒸发量为29.3 mm,占林冠截留模拟值的27.8%;降雨停止后的树干蒸发量为2.1 mm,占林冠截留模拟值的2.0%。基于修正的Liu 模型计算得到总林冠截留量为96.0 mm,模拟值与实测值相对误差为9.0% (图6a)。综上,两个模型都低估了一个雨季的总林冠截留量(图6a)。根据Muzylo 等[8]对模型效果的评价,修正的Gash 模型模拟效果非常好,修正的Liu 模型模拟效果良好;修正的Gash 模型相对误差低于修正的Liu 模型,对总截留量模拟更准确。

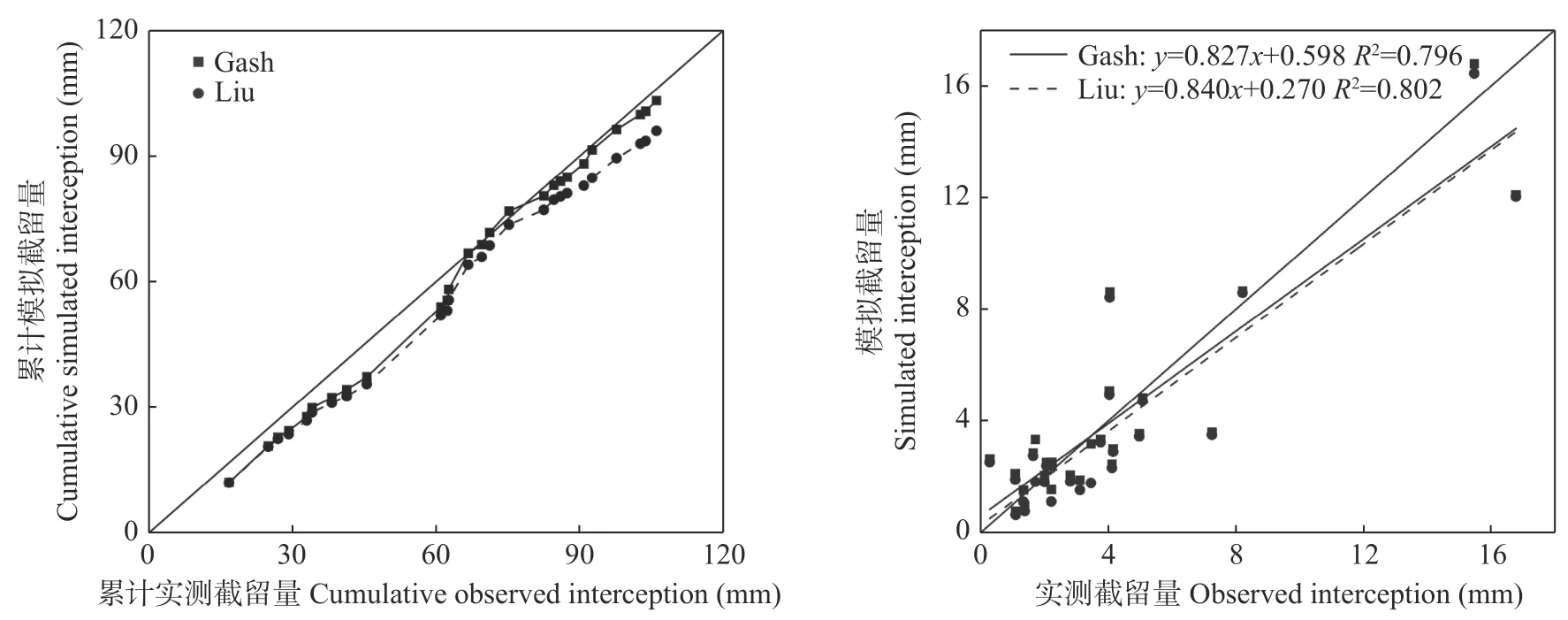
图6 修正的Gash 模型及Liu 模型截留量模拟效果Fig.6 Interception simulation performance of the revised Gash model and Liu model

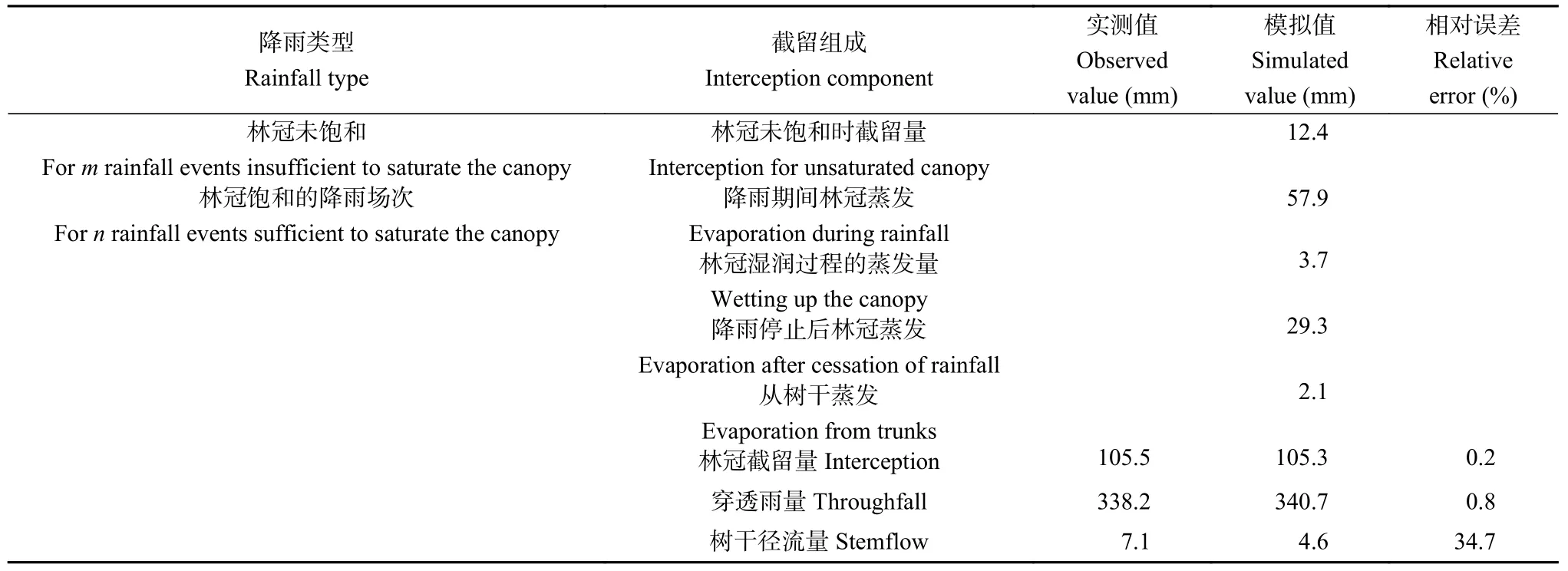
表3 修正的Gash 模型降雨再分配要素模拟结果Table 3 Simulation results of rainfall partitioning of revised Gash model

利用修正的Gash 模型及修正的Liu 模型对次降雨林冠截留量进行模拟。结果表明,对于次降雨截留量的模拟,两个模型模拟效果均较好,修正的Liu模型模拟效果(R2=0.802) 略优于修正的Gash 模型(R2=0.796) (图6b),两个模型在大部分小降雨事件时均低估了截留量(图6b)。

2.3.3 模型参数敏感性分析

对Gash 模型的6 个参数进行敏感性分析(图7)表明,林冠平均蒸发速率、林冠持水能力、冠层盖度、树干径流系数、树干持水能力与截留量为线性正相关关系,而降雨强度与截留量为负相关关系。当林冠平均蒸发速率、林冠持水能力、冠层盖度、树干径流系数、树干持水能力分别增加10.0%,林冠截留量分别增加5.9%、3.2%、0.8%、0.04%、0.2%,平均降雨强度增加10%,林冠截留率减小5.4%。综上,修正的Gash 模型参数敏感性排序: 林冠平均蒸发速率>平均降雨强度>林冠持水能力>冠层盖度>树干持水能力>树干径流系数。

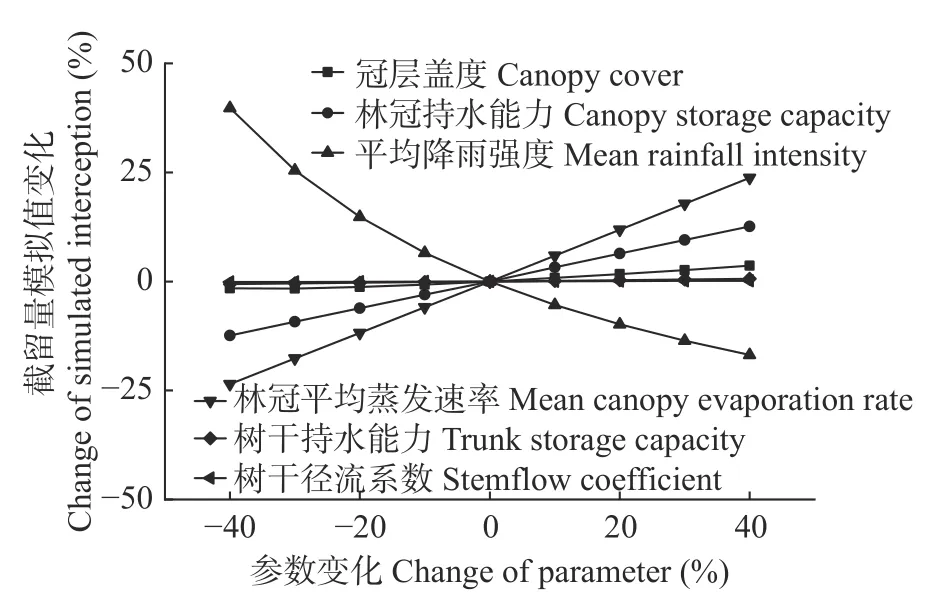
图7 修正的Gash 模型的参数敏感性分析Fig.7 Sensitivity analysis of revised Gash model parameters

3 讨论

3.1 降雨再分配规律

太行山典型油松林林冠截留率、穿透雨率、树干径流率分别为23.4%、75.0%、1.6%。本研究总结了中国部分地区油松林降雨再分配特征(表4),并发现其平均林冠截留率为21.5% (13.47%～31.67%),平均穿透雨率为74.9% (67.08%～84.00%),平均树干径流率为3.9% (0.52%～22.5%)。同一林型在不同研究区降雨再分配规律不同,这是由降雨特征、冠层结构差异所致。

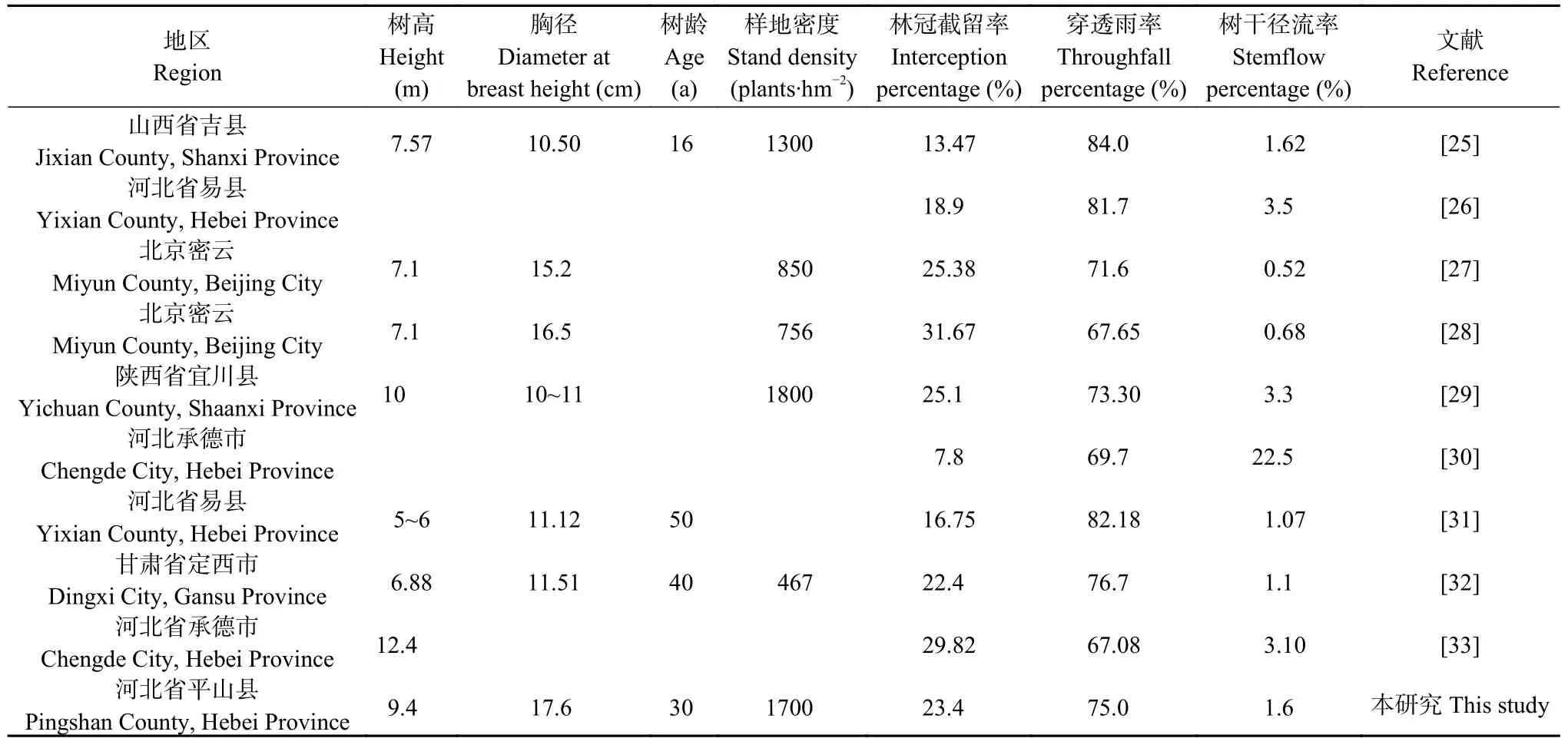
表4 不同地区油松林降雨再分配规律Table 4 Rainfall partitioning patterns of Pinus tabulaeformis forests in different regions

降雨量与林冠截留量、林冠截留率为幂函数关系,林冠截留量存在最大饱和容量,随着降雨量的增加林冠截留率降低并趋于稳定(图4),这与武秀荣等[34]对青海云杉的研究结果一致。当冠层未达到冠层饱和容量时,截留量增加速度较快,此时的截留率较大,而当冠层达到饱和容量之后,随着降雨量的增加,截留量增加速度变慢,且截留率开始降低[35]。

随着降雨量增加,穿透雨量呈线性增加趋势(图2a),这与Deng 等[12]和Francis 等[36]的研究结果一致。不同树种穿透雨量和穿透雨率不同,Yue 等[37]研究表明阔叶树种的穿透雨率大于针叶树种;同一树种由于冠层结构、树龄不同,穿透雨率也不同。本研究得到油松林穿透雨率为75.0%,低于胡珊珊等[31](82%)和次仁曲西[25](84%)的研究结果。降雨量与穿透雨率为幂函数关系(图2b),这与黄团冲等[38]研究结果一致,当降雨量较小时,林冠未饱和,穿透雨主要以自由穿透雨(经林冠间隙滴落的穿透雨)为主,而随着降雨量增大,冠层逐渐达到饱和,穿透雨主要以滴落穿透雨(经叶片枝干表面滴落的穿透雨)为主。

降雨量与树干径流量呈线性函数关系(图3a),这一结果与胡珊珊等[31]、Exler 等[39]的研究结果一致。本研究得到油松林树干径流率为1.6%。Ma 等[40]研究表明油松、刺槐的树干径流率分别为0.7%、1.3%,刘效东等[41]发现季风常绿阔叶林的树干径流率为4.5%。不同树种产生树干径流的阈值不同,本研究得到油松产生树干径流的阈值为5.5 mm,Deng等[12]研究表明樟子松(Pinus sylvestrisvar.mongolica)产生树干径流的阈值为5 mm,柴汝杉等[42]研究发现原始红松林(Pinus koraiensis)产生树干径流的阈值为10 mm,张继辉等[43]研究表明马尾松(Pinus massoniana)产生树干径流的阈值为2.2 mm。由于不同树种的树皮粗糙度、冠层结构等不同,树干径流量也存在一定差异。树皮越粗糙,产生树干径流所需要的降雨阈值越高。

3.2 降雨截留模型

基于修正的Gash 模型计算得到林冠截留量为105.3 mm,截留量实测值为105.5 mm,相对误差为0.2%。Liu 模型计算得到林冠截留量为96.0 mm,模拟相对误差为9.0%。众多学者使用修正的Gash 模型及Liu 模型对林冠截留量进行了模拟,如Shi 等[19]使用修正的Gash 模型对华山松林冠截留过程进行模拟,结果表明,模拟值低估了5.87%;王晓燕等[22]对北京密云水库区油松林进行模拟,林冠截留量模拟值和实测值的相对误差为18.02%。Carlyle-Moses 等[24]研究表明修正的Gash 模型及Liu 模型都低估了林冠截留量。本研究使用修正的Gash 模型及修正的Liu模型模拟油松林截留量,两个模型相对误差较小,且都低估了截留量,主要表现为大多数小降雨事件时对截留量的低估(图6a),这与Fan 等[44]的研究结果一致。修正的Gash 模型在小降雨事件时只考虑冠层盖度,而忽略了气象特征对截留量的影响。在研究期间,小雨次数占总降雨次数的58%,因此模型低估了总截留量。

不同研究中截留模型参数敏感性不同。本研究表明林冠平均蒸发速率和平均降雨强度是影响截留量的两个最敏感参数(图7),这与Fan 等[44]研究结果一致。降雨过程的林冠蒸发量主要受降雨强度和林冠蒸发速率的影响,当降雨强度增大时,林冠截留量减小[13]。林冠持水能力是影响模型精度的一个重要参数[19],王晓燕等[22]等利用回归法得到林冠持水能力为1.45 mm,本研究利用回归法得到的林冠持水能力为1.54 mm,Llorens 等[45]研究表明针叶林林冠持水能力一般在0.3～3.0 mm,因此本研究结果在合理范围内。林冠持水能力受到冠层结构和降雨特征[13,40]等因素的影响,因此不同区域、不同植被类型林冠持水能力也不相同。冠层盖度也会影响截留量,冠层盖度增加,穿透雨减小,林冠截留量增加[13]。林冠未饱和时,林冠截留只受到冠层盖度的影响,随着冠层盖度的增加,林冠截留量增加。树干径流系数和树干持水能力是敏感性较低的两个参数,这与Su 等[13]和Fan 等[44]研究结果一致。

虽然修正的Gash 模型及修正的Liu 模型可用于预测太行山区油松林林冠截留量,但截留模型本身也存在一些问题: 1)两个截留模型没有考虑风速对截留量的影响;2)当林冠未饱和时,Gash 模型仅考虑冠层盖度对截留量的影响,没有考虑降雨强度等因素;3)模型参数的准确性影响截留量估算,目前模型大多数参数基于线性方程推求,未来研究中需通过实测法来获取模型的某些特定参数,如林冠持水能力参数。