右端不连续免疫对双线性病毒变异模型的影响
2023-12-27李迅,陶龙
李 迅,陶 龙
(1.江苏联合职业技术学院南京卫生分院,江苏 南京 210038;2.皖南医学院公共基础学院,安徽 芜湖 241000)
在人类社会的发展过程中,传染病总是伴随左右,始终威胁着人类的生存[1]。 尽管医疗防治水平已有很大提高,但像由新型冠状病毒、埃博拉病毒和猴痘病毒[2-4]等引起的传染病仍然威胁着各国人民的生命健康安全。
建立传染病模型,进行定性和定量分析,是研究传染病的重要方法。 W. O. Kermack 等[5]建立了SIR 舱室模型,研究了传染病的阈值理论。考虑到病毒在传播过程中会发生变异,A. P. Dobie[6]提出并研究了一类具有病毒突变的SIS 传染病模型,发现当病毒发生变异时会导致一种死亡率很高的疾病发生。G. R. Jiang 等[7]提出了具有脉冲和种群变化的SIS 模型,并研究了其周期解的存在性和稳定性。 李俊[8]研究了病毒自身发生变异的传染病模型
通过引入恰当的Lyapunov 函数证明了模型平衡点的全局渐近稳定性。 在文献[8]基础上,班相函等[9]考虑了时滞对模型的影响,研究了系统的Hopf 分支的时滞临界点,提出了几种控制疾病的方法。以上研究都是建立在连续函数基础上的,而当某种病毒开始传播时,人们尚未发现其危害,不会给予高度关注,但随着时间的推移,人们一旦发现这种病毒的危害,就会立即采取防治措施。 因此,感染者数量总体上是不连续的。
为了精准研究病毒的传播情况, 我们建立了右端不连续的双线性病毒变异模型, 给出了模型的种群基本再生数R0,通过构造Lyapunov 函数和使用LaSalle 不变集证明了R0>1时模型的解将全局渐近收敛于有病平衡点,R0<1时模型的解将全局渐近收敛于无病平衡点,并通过MATLAB 数值仿真验证结论的正确性。
1 模型的建立
以文献[8-9]为基础,建立微分模型
其中,S为易感染者人数,I1为变异前患者人数,I2为变异后患者人数,A为种群的输入率,µ为自然死亡率,β1为变异前患者的传染率,β2为变异后患者的传染率,γ1为变异前患者的康复率,γ2为变异后患者的康复率,ε为变异前的患者向变异之后患者的转化率,以上参数均为正数。
记微分模型的初值为S(0)、I1(0)和I2(0),模型的种群基本再生数
将模型(1)的3 个方程相加,可得
即dNdt=A−µN,其中N=S+I1+I2。
若N>A µ,则有dNdt<0,从而有N(t) 为了得到本文结论,作如下假设。 假设1:h(I1)=ϕ(I1)I1,其中ϕ:(0, +∞) → (0, +∞)是单调递增的分段连续函数,h(I1)仅有可数个孤立的不连续点{pk}。 由于模型(2)中关于dS(t) dt和dI1(t) dt的方程右端是非连续的, 故连续方程的解理论不适用于模型(2)。 因此,我们考虑采用Filippov 解[10]。 对于一类不连续的微分方程,它的Filippov 解定义为 其中,f(t,x)是关于t 和x(t)可测的不连续函数,且局部有界,即f∈(R ×Rn, Rn)。 定义1[11]:对于集值映射K是加在f上的算子,F(t,x)是由f(t,x)构成的集合,若f(t,x)在一点处连续,则F(t,x)构成单点集合,若f(t,x)在一点处不连续,则F(t,x)构成一凸闭包集合。 由定义1 可知,式(3)是存在于凸闭包F(t,x)中的函数,即dxdt∈F(t,x),t∈[0,T)。 由Filippov 解的定义可知,右端不连续微分模型的解是绝对连续的向量函数,即Filippov 解(S(t),I1(t),I2(t))在[0,T)上绝对连续,且满足 若假设1 成立,式(4)的平衡点满足微分包含 对于有病平衡点,设(S*,I1*,I2*)是式(4)的有病平衡点,则有 很明显,若(S*,I1*,I2*)是式(8)的平衡点,则存在使得0=β1S*I1*+β2S*I2*− (µ+γ1+ε)I1*−ξ*,其中ξ*是唯一的,且ξ*=β1S*I1*+β2S*I2*−(µ+γ1+ε)I1*∈[ϕ(I1∗)]I1∗。 联立式(7)中的微分方程,可得 令 求函数g(I1)的导数,可得 因为所有参数均为非负数,所以有g′(I1) <0,即g(I1)是单调递减函数, 因此对于无病平衡点,有如下结论。 引理:如果R0>1,那么是式(10)中的唯一正解,并且满足 其中 证明:先证明解的存在性。 因为R0>1,所以有g(0)>ϕ(0) > 0。由于g(I1)是单调递减函数,ϕ(I1)是单调递增函数, 因此g(I1) ≤0成立的充分必要条件是I1满足 由假设1 可知ϕ是单调递增函数,记 则有f≥0。式(11)中的两式相减,两边再同除以I1*−I1**,可得 这与两边相等矛盾,说明假设不成立,因此微分包含(9)有唯一正解。 下面证明模型(2)的平衡点的全局渐近稳定性。 对于有病平衡点(S*,I1*,I2*),由及可知 假设2:若R0>1,则ϕ(I1)在I1*处有一个跳跃间断点,其中I1*是式(10)所确定的唯一正解,且 根据假设2,定义 则有θ> 0。 定理1:若假设1 和假设2 成立,则式(4)满足初值S(0) ≥0,I1(0) ≥0,I2(0) ≥0的所有解全局稳定于有病平衡点E*=(S*,I1*,I2*),且在有限时间内趋于稳定,即当 时,有(S(t),I1(t),I2(t)) =(S*,I1*,I2),其中 构造Lyapunov 函数 其中,α是一个可以确定的正常数,后面将给出其取值范围。 显然V1(x(t),y(t),z(t))是关于(x(t),y(t),z(t))的正则函数。 当(x(t),y(t),z(t)) ≠0时,V1(x(t),y(t),z(t)) >0;当且仅当V1(0,0,0) =0;当x(t)→ +∞或y(t) → +∞或z(t) → +∞时,有V1(x(t),y(t),z(t)) → +∞。 对V1(x(t),y(t),z(t))求关于t的导数,有dV1dt= 由假设2 可知,若(x(t),y(t),z(t)) ≠0,则有[η(t)−η*]2>θ2,故对于任意的t∈{t:(x(t),y(t),z(t))≠(0,0,0)},有 对dV1dt从0 到t进行积分,有 令 由文献[12]可知,当 时, 对任意的t,都有(x(t),y(t),z(t)) =0,故有(S(t)−S*,I1(t)−I1*,I2(t)−I2*) =(0,0,0),即当t>t*时,有(S(t),I1(t),I2(t)) =(S*,I1*,I2*)。 下面证明模型(2)的解在无病平衡点的全局渐近收敛性。 由于假设1 不符合右端不连续的假定,因此给出以下假设。 假设3:h:(0,+ ∞ ) →(0,+ ∞)是单调递增且至多存在有限个间断点的函数,I1=0是函数h(I1)的间断点,且h(0) = 0。 定理2:若模型(2)满足假设3,则当R0<1时,它的解都将在有限时间内全局稳定于无病平衡点即当t>t*时,有 证明:令x(t)=S(t)−S0,则模型(2)变为 对V2(x(t),I1(t),I2(t))求关于t的导数,可得 由R0<1,0≤β1≤1,0≤β2≤1可知, 由假设3 可知η(t) ≥h(0+),因此有≤−µh(0+)。两边做从0 到t的积分,可得0≤V2(x(t),I1(t),I2(t))≤V2(x(0),I1(0),I2(0))−µh(0+)t。 令V2(x(0),I1(0),I2(0))−µh(0+)t=0,即可求得 现在将运用MATLAB 软件仿真模拟验证结论的正确性。 由假设1 和定理1 可知,当R0>1时,模型(2)的解将在有限时间内全局渐近收敛于平衡点E*=(S*,I1*,I2*)。选取参数β1=0.01,β2=0.3,µ=0.2,γ1=0.9,γ2=0.9,ε=0.1,A=50,设置初值(S(0),I1(0),I2(0)) =(100,150,200),R0=7.7,选取不连续函数 则模型(2)的解在E*全局渐近收敛,结果如图1 所示。 图1 >1时模型(2)的解在的全局稳定性 由假设3 和定理2 可知,当R0<1时,模型(2)的解将在有限时间内全局渐近收敛于平衡点E0=(S0,0,0)。选取参数β1=0.2,β2=0.2,µ=0.8,γ1=0.8,γ2=0.1,ε=0.1,A=5,设置初值(S(0),I1(0),I2(0)) =(10,15,20),R0=0.82,选取不连续函数 则模型(2)的解在E0全局渐近收敛,结果如图2 所示。 图2 <1时模型(2)的解在的全局稳定性 为了分析非连续治疗策略对病毒变异传染病模型的影响,我们通过引入右端不连续治疗函数h(I1),研究了模型各平衡点的存在唯一性。通过研究发现:当R0>1 时,在有限时间内,模型的所有Filippov 解全局渐近收敛于有病平衡点E*;当R0<1 时,在有限时间内,模型的所有Filippov 解全局渐近收敛于无病平衡点E0。 这说明“有限时间内被治愈”具有重要的现实意义, 因为患者总是想知悉他们的病能否被治愈、何时能被治愈。 我们利用MATLAB 软件对此不连续模型进行了数值仿真,验证了定理1 和定理2 的正确性。 在今后的研究中,我们将把Filippov 解和微分包含理论应用到更多的生物动力学系统[13-14],以获得更加符合实际的结论。2 平衡点的存在唯一性
3 稳定性分析
4 数值分析
4.1 有病平衡点的数值分析
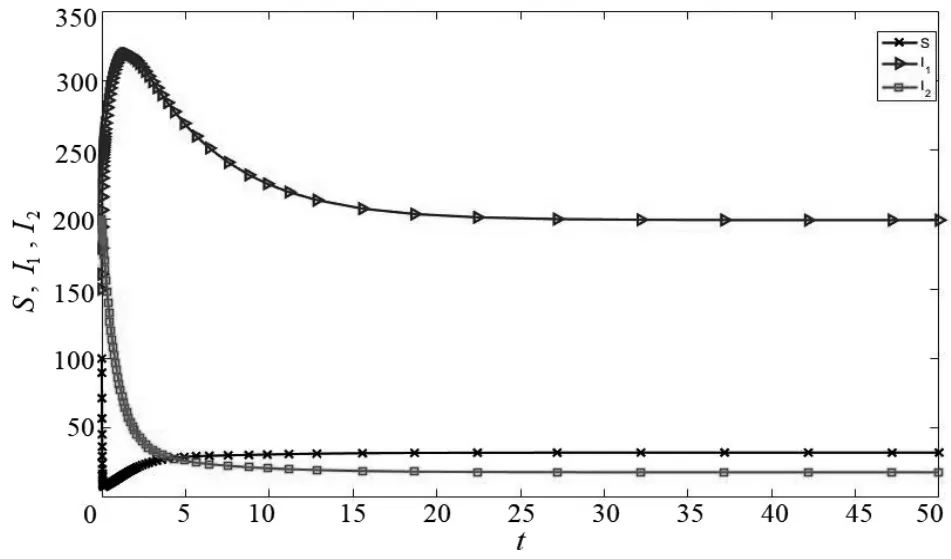
4.2 无病平衡点的数值分析
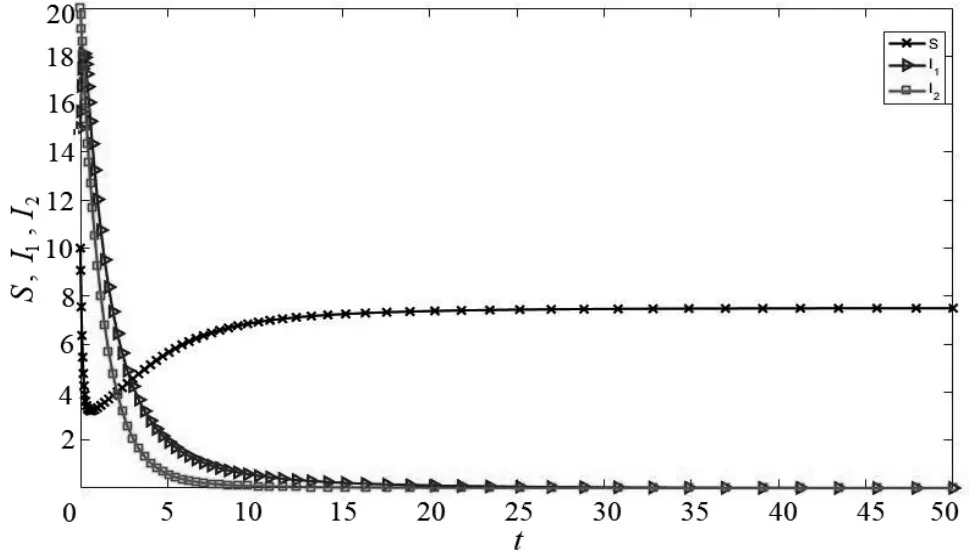
5 结束语
