基于三阶段DEA-Tobit模型的城市轨道交通运营效率测度分析
2023-12-27王永岗罗贤雨陈俊先马超群
王永岗,罗贤雨,陈俊先,马超群
(长安大学 运输工程学院, 陕西 西安 710018)
0 引 言
城市轨道交通以安全、高效、节能等优点越来越受到大中城市的青睐。根据城市轨道交通协会统计数据,截至2022年底,我国大陆地区已有55个城市开通并运营了城市轨道交通,线路达到308条,总里程达到10 287.45 km,在建总里程达到6 350.55 km。作为一项公共事业,城市轨道交通带有明显的福利性质,呈现出投资多、回报慢、票价低、服务强度大等特点,需要依靠政府财政补贴来维持其正常的运营,故如何以较少投入使运营效率最大化则是亟待解决的核心难题之一[1]。因此,对城市轨道交通的运营效率测度问题进行研究具有重要的现实意义。
关于城市轨道交通运营效率的测度问题,国内外学者主要从宏观层面进行了分析,包括政策和组织模式等[2]。张剑寒[3]以社会效益为产出指标,运用数据包络分析法(data envelopment analysis,DEA)探讨了PPP (public-private partnership)模式对城市轨道交通运营效率的影响;P.JAIN等[4]和F. QIN等[5]分别研究了股权私有化和组织模式对城市轨道交通运营效率的影响,对运营效率提升具有积极意义。此外,相关学者还从运营效率评估层面展开了研究。李磊等[6]基于DEA和MI (malmquist index)指数,对城市轨道交通动态运营效率进行了分析;H.ZHANG等[7]、张浩等[8]、XUE Liang等[9]、周柯廷等[10]、焦柳丹等[11]分别运用松弛措施DEA模型、BCC (banker charnes cooper)模型、DEA- Malmquist生产力指数- Tobit回归混合模型、Super-SBM模型及超效率SBM-Malmquist模型对不同城市的轨道交通运营效率进行了测度分析。
国内外已对轨道交通运营效率研究进行了诸多有益尝试,但传统的DEA模型针对效率测度的排序和趋势分析等问题未进行改进,没充分考虑外部环境及随机因素的影响[2],故决策单元间不一定具有可比性,易导致测度结果失真。另外,现有研究中往往只关注如何去量化运营效率,缺乏对影响因素的进一步深度分析。鉴于此,笔者应用三阶段DEA模型对城市轨道交通的运营效率测度进行了分析,对比研究了剔除环境和随机因素影响前后运营效率差异,并利用Tobit模型结合实证结果对运营效率的影响因素进行探究,以便提出能有效提升运营效率的措施建议。
1 研究方法
1.1 三阶段DEA模型
作为复杂的巨系统,城市轨道交通运营不仅受到技术管理等内生因素影响,同时也受社会经济、交通环境、结构模式等外生因素干扰,故传统模型难以准确测度其效率。H.O.FRIED等[12]提出的了三阶段DEA模型,能有效地消除环境与随机因素干扰,以便进行精准决策。
1.1.1 初始效率分析
以城市轨道交通的系统作为决策单元(decision making unit, DMU),根据其运营特点,采用以投入为导向的BCC模型进行效率测度。作为传统DEA模型的扩展,BCC模型假设决策单元的规模效益可变,继而将初始技术效率 (technical efficiency, TE)分解为纯技术效率(pure technical efficiency, PTE)和规模效率(scale efficiency, SE),分别反映了轨道交通系统在技术管理因素及生产规模因素所影响下的运营效率[12]。
假设有n个被测度的轨道交通系统,并分别拥m种输入指标和s种输出指标(j=1, 2, …,n;i= 1, 2, …,m;r=1, 2, …,s),则模型的对偶形式为:
(1)
式中:Xij、Yjr分别为第j个DMU的第i项投入指标和第r项产出指标;X0、Y0分别为被测度DMU的投入和产出变量;S+、S-分别为投入不足和产出冗余;θ为初始运营效率;ε为无穷小量。
BCC模型在进行效率测度时将测度对象简化成投入产出系统,缺乏对环境及随机干扰项考虑。
1.1.2 相似随机前沿模型(SFA)
在初始效率分析中,松弛变量反映了各轨道交通系统初始的低效率[11]。以其为被解释变量,对环境变量、管理因素及随机干扰项进行SFA (stochastic frontier approach)回归分析,进而可得到各参数的真实影响。
令i= 1, 2, …,I和n= 1, 2, …,N,构建回归模型为:
Sni=f(Zi;βn)+vni+μni
(2)
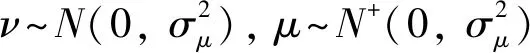
参考文献[13]对低效率分离的研究,在SFA回归参数基础上采用成本函数的形式对变量进行分离,并对原始投入进行调整,如式(3)。
(3)
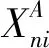
1.1.3 调整后效率评估
1.2 Tobit回归分析
考虑到效率测度结果是处于[0, 1]区间的间断值,选用因变量受限的Tobit模型对效率影响因素进一步探索分析,构建回归模型如式(4):
(4)
式中:Y′为截断因变量向量;Y为效率值向量;X为影响因素;α为回归系数;μ~(0,σ2)为误差项。
2 指标及数据说明
2.1 指标选取
为准确描述城市轨道交通系统的投入产出特性,并满足模型对选取变量的约束,选择线路运营里程与车站数作为规模投入的测度指标。线路设备是列车运行基础,而车站作为客流吸引的直接场所,其选址状况及周边配套服务设施与客流吸引量存在直接关系,这两者前期投入巨大,能反映投入状况。在资源投入方面,参考已有成果[3, 6-9],同时从人力、物质资源等入手,选择运营人员数与日均列车开行次数作为测度指标,这两者作为城市轨道交通运营直接投入的生产要素,可有效地体现系统日常的运营织策略;同时结合产出状态,可进一步反映列车运能的虚糜状况。在产出方面,选择客运周转量作为测度指标,可表现城市轨道交通对完成乘客出行所做的贡献,构建BCC测度模型。
为满足“分离假设”,环境变量应采用对效率有影响但模型未能涉及的因素[13]。在26个决策单元中,由于各城市产业结构、交通环境、社会经济状况、居民出行习惯等不同,城市轨道交通的运营环境也存在差异,如旅游城市比工业城市拥有更大的出行强度,故可确定的环境变量包括竞争环境、制式结构、线网条件、服务需求及车辆基地等5个要素。其中,竞争环境以市区公交线网密度作为代理变量,其值为市区公交线路长度与用地面积之比,用于反映外部交通环境;伴随着网络化条件的实现,列车运营组织难度上升,且在客流吸引力上也表现出较大差异,故线网条件限定为同时拥有4条线路或3个以上换乘节点的城市轨道交通系统;考虑到各个城市产业结构与政策不同,居民出行习惯与出行强度也不同,服务需求定义为城市当年的公交出行人次。此外,定义了其它变量,便于后续分析影响因素,如表1。

表1 模型指标体系
2.2 数据说明
考虑数据的可获取性,选择2018年我国26个典型城市作为决策单元,对城市轨道交通的运营效率进行测度分析。其中:竞争环境、服务投入及服务需求等数据根据各城市统计年鉴、国民经济发展公报及地铁官网整理统计得到;投入产出数据、其它变量及环境变量中的其它指标数据均来源于《城市轨道交通2018年度统计和分析报告》。
3 实例分析
3.1 初始效率分析
使用DEAP 2.1软件对26个决策单元进行运营效率测度,结果如表2。
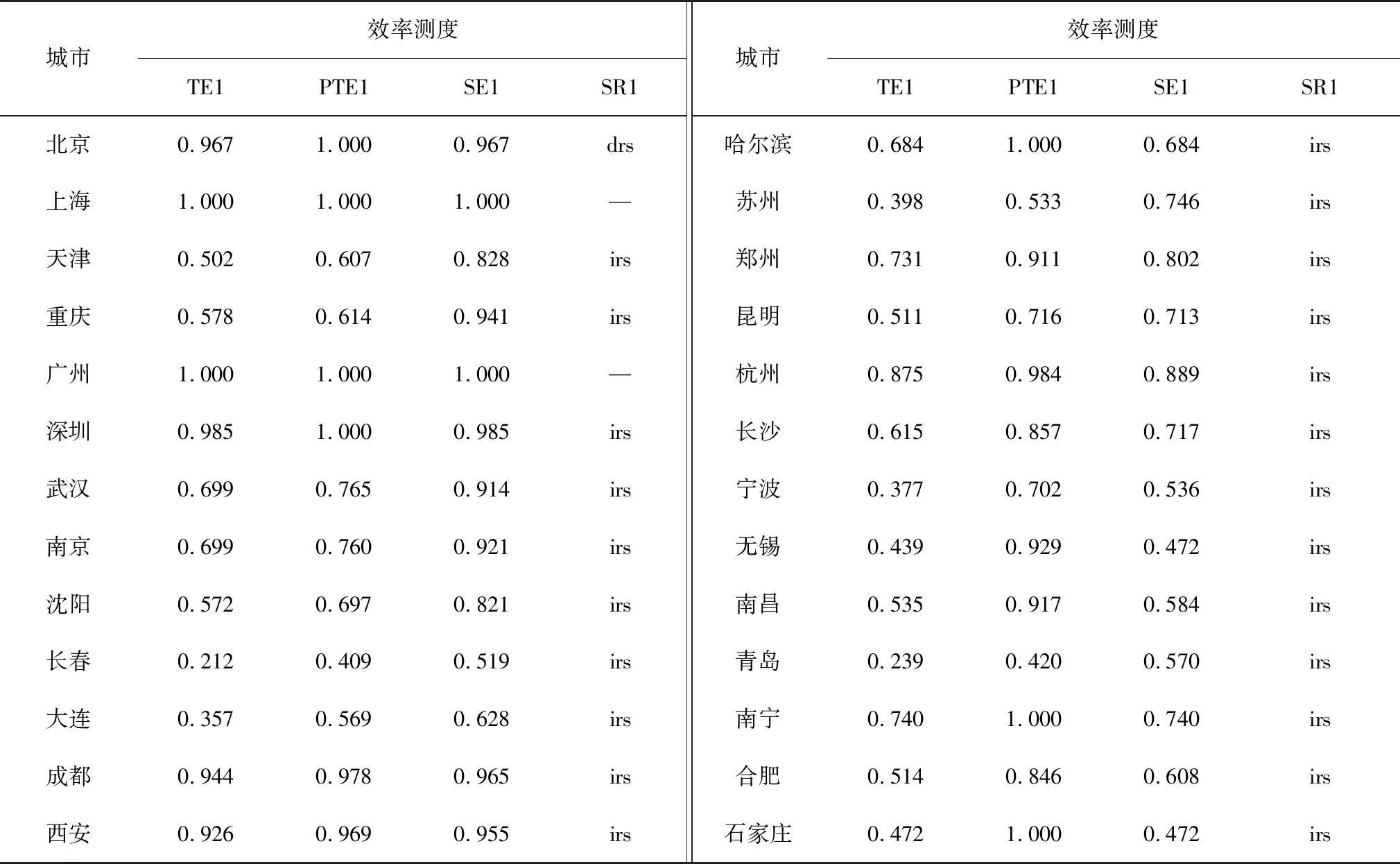
表2 我国典型城市轨道交通运营效率测度结果(调整前)
在不考虑环境变量与随机干扰情况下,2018年我国城市轨道交通平均技术效率为0.637,平均纯技术效率为0.815,规模效率为0.768。其中,上海和广州的DEA均为有效,产出了最大化的客运量。从纯技术效率而言,有7个城市达到了前沿面,反映出了较高的运营技术与管理水平;从规模效率看,有13个城市低于平均值,且整体水平偏低,说明多数城市的轨道交通系统正处于发展阶段,如何吸引客流、提升运输规模是下一阶段关键[14-15]。
3.2 SFA回归分析
为进一步分析环境变量和随机干扰对效率测度结果的影响,应用Stata14软件对初始效率所产生的松弛变量和环境因素进行SFA回归分析,并对投入变量进行调整,结果如表3。由表3可知:各项投入分别在10%、5%、1%显著性水平下通过LR单边检验,这说明SFA模型具有合理性与必要性,环境变量对低效率产生存在显著影响。各项松弛变量对环境变量回归的γ值分别为0.998、0.997、0.986、0.995,接近于1,且均能在1%的显著性水平下通过检验,这说明相较于环境因素,随机干扰影响较小,但仍对效率测度存在重要影响。
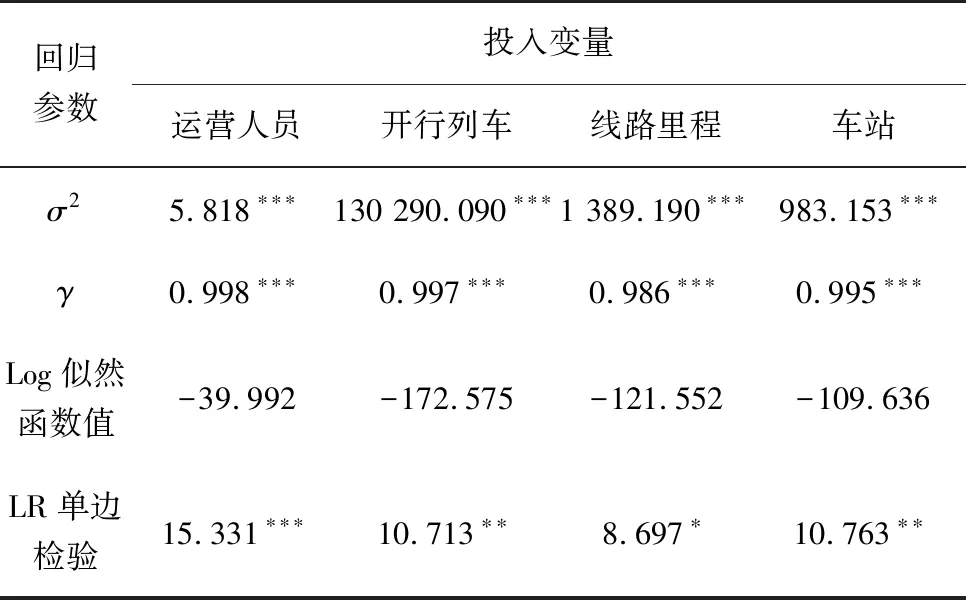
表3 SFA回归结果
3.3 调整后效率评估
基于SFA回归参数对管理无效率进行分离,并通过式(3)对投入变量进行调整,保持产出不变,再次对运营效率进行测度,结果如表4。调整后技术效率均值为0.456、纯技术效率均值为0.942、规模效率均值为0.480。

表4 我国典型城市轨道交通运营效率测度结果(调整后)
计算调整前后的效率值与产出指标间Spearman等级相关系数分别为0.746、0.984,满足p<0.001。显然,调整后的效率值更能真实地反映出决策单元内部管理水平,且综合考虑环境变量与随机干扰能对效率测度起到积极作用。
3.3.1 调整后的效率分析
通过综合考虑环境变量和随机干扰,我国26个城市轨道交通的平均综合效率为0.456,平均纯技术效率为0.942,其中有9个城市达到技术前沿面,平均规模效率为0.480,运营效率主要为纯技术效率所主导,这说明我国的轨道交通在运营组织及技术设备使用开发方面已较为成熟,但现有条件下的运营规模与有效规模相差较大,特别是城市轨道交通新兴城市,规模不足致使城市轨道交通的灵活性与可达性受到限制,无法吸引客流。
对此,应进一步完善周边配套交通设施建设,提高既有线路的辐射范围,同时还应充分利用地铁创造各种派生资源,完善上盖物业建设,鼓励“地铁运营+多元开发”模式带动居民出行,从而回馈给城市轨道交通更多客流。在26个决策单元中,有25个为规模效益递增,这说明增加规模、优化资源结构将有助于提高运营效率。其中北京呈现出规模效益递减的情况,这说明该城市轨道交通线网已趋于成熟,现有条件下的规模扩张能使线网可达性及便捷度更高,但线网客流饱和度正逐渐下降,故未来发展重点应结合客流支撑状况对骨干网及周边进行加密,同时应充分利用常规公交(中低运量制式),并考虑与长途客车、铁路等干线枢纽进行衔接,以进一步吸引乘客,提升网络化水平。
3.3.2 调整前后对比分析
调整前后城市轨道交通运营效率变化如图1。
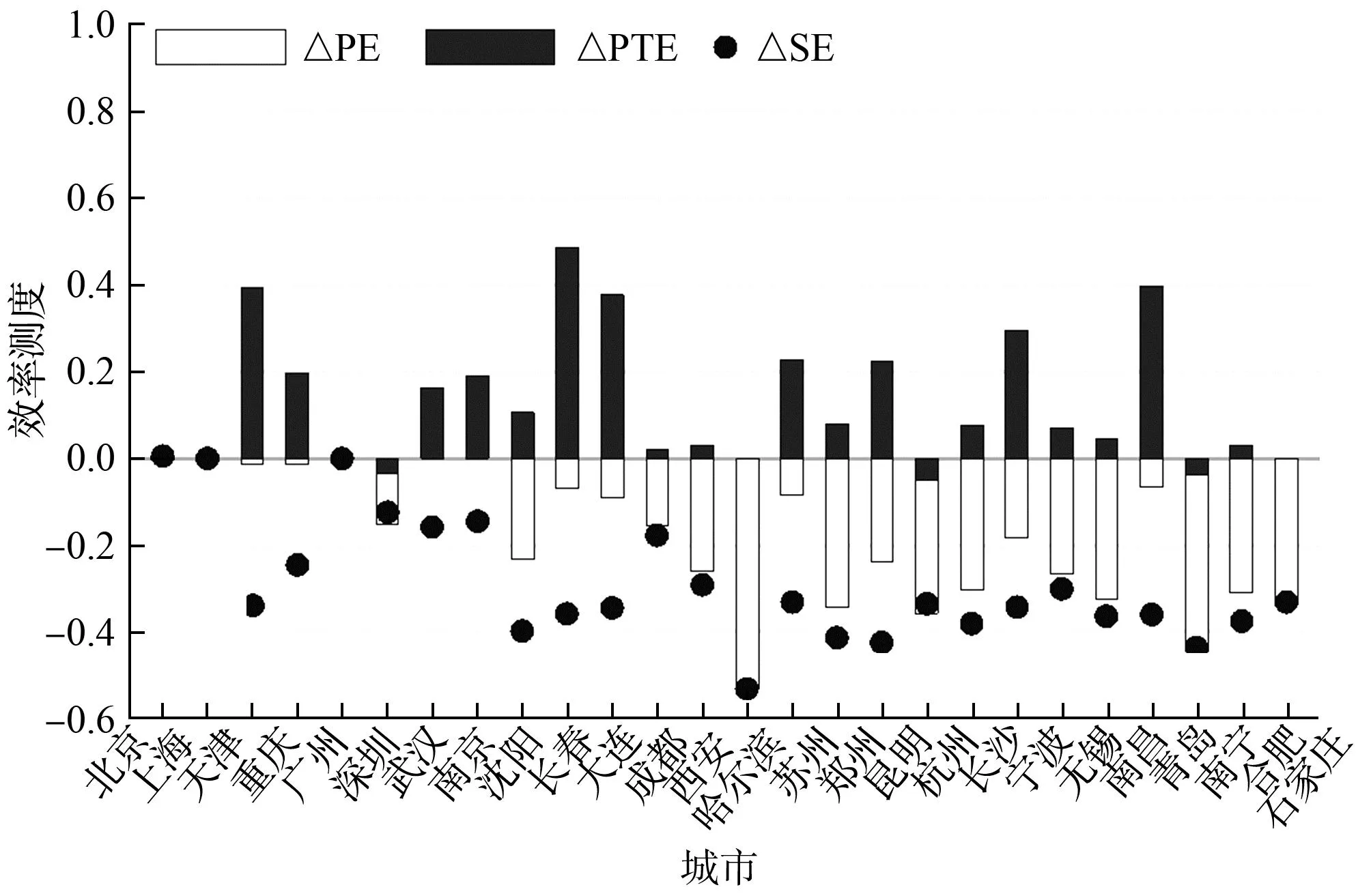
图1 整前后城市轨道交通运营效率变化
由此可见,在调整后城市轨道交通综合技术效率出现了显著下降(平均下降0.181),规模效率平均下降0.288,综合技术效率降低主要是由于规模效率下降所致。这说明我国多数城市的轨道交通系统规模效率并不像调整前那样靠近前沿面,尤其是一些新兴城市的轨道交通(如:合肥、石家庄、哈尔滨等)仍存在较大上升空间。纯技术效率则有一定提升,平均上升0.127,其中:天津、长春、大连、青岛等城市平均上升0.414。这些城市以发展轻轨、有轨电车等为主,客运规模较小,调整前可能难以反映其真实运营水平。这也说明我国城市轨道交通实际运营中的资源配置能力已较强,运营技术渐趋优化。
3.4 运营效率影响因素分析
通过基于Tobit模型对效率测度结果与影响因素进行逐一回归分析来量化各影响因素影响力,以便进一步探究提高轨道交通运营效率的条件与方法,结果如表5,表明是否形成线网×线路里程与运营效率显著相关。城市轨道交通系统成网后,随着线路里程增加,其运营效率亦会相应提升;未成网条件下的规模扩张反而会使得运营效率下滑,表明了城市轨道交通系统网络化运营至关重要。
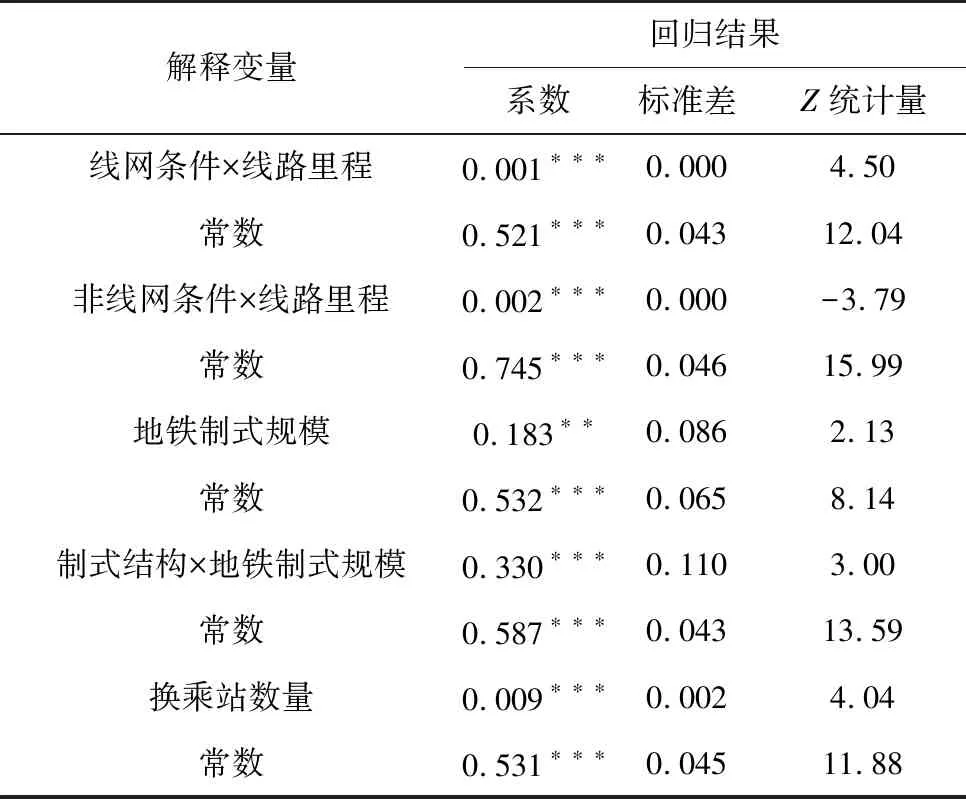
表5 Tobit回归结果
地铁制式规模与运营效率显著正相关,回归系数为0.183 (p<0.01),这说明地铁已然成为城市轨道交通运营的中坚力量;地铁规模×制式结构与运营效率回归系数为0.330 (p<0.001),这表明多制式结构对客流吸引具有积极作用;换乘站数量与运营效率回归系数为0.009 (p<0.001),这表明换乘站投入是影响运营效率的重要因素,每提高一个单位,运营效率将提升0.009个单位。
4 结 语
通过选用三阶段DEA-Tobit模型对我国城市轨道交通系统的运营效率问题进行了分析,结果表明:其综合效率较低,而纯技术效率较高,且前沿面与重点发展低运量制式的城市更应注重外部环境协调。采用Tobit回归模型对城市轨道交通系统运营效率影响因素进行了分析,发现线网规模、制式结构及换乘站数量等显著影响运营效率。
为有效提升城市轨道交通系统的运营效率,不同城市应根据自身需求,积极扩大运营规模,优化资源结构;要充分协调好轨道交通与其它地面交通的竞争与合作关系,优化外部运营环境,完善换乘机制与车站周边基础交通设施建设(如:规划停车场、出租车停靠点,公交换乘引导等),当换乘距离较大时可增设雨棚、连廊等慢行设施及共享单车租赁点,进一步扩大车站辐射范围来吸引乘客。城市轨道交通建设中应努力形成网络化运营,优化行车组织方案,在重点发展大运量制式的同时应因地制宜实现多种制式结构的城市轨道交通系统协调发展,如拓展中低运量补充线或快速通勤的市域快线等。
